基于非线性有限元理论的钢管混凝土和钢筋混凝土力学性能研究
2015-12-04付明春苏德利
付明春,苏德利
(大连海洋大学,辽宁大连116300)
随着高层、大跨度结构不断涌出,这使得以钢筋混凝土结构为主的结构形式遭遇巨大挑战。原因在于钢筋混凝土结构存在自重大、抗震性能差、易开裂等缺点,无法有效地应用到高层、超高层、大跨度结构。而钢管混凝土所具有的承载力高、抗震性好等特点都是高层、超高层、大跨度结构建设所需要的。但目前,我国对钢管混凝土力学性能的研究较少,这不利于钢管混凝土的推广应用。为更好地研究钢管混凝土的力学性能,采用ANSYS非线性有限元理论,借助比较成熟的钢筋混凝土理论,建立钢管混凝土与钢筋混凝土非线性有限元模型,对二者的力学性能进行分析比较。
1 概述
1.1 钢筋混凝土的发展和研究
对于钢筋混凝土而言,主要经历了三个不同的发展阶段。第一阶段,从钢筋混凝土结构发明到20世纪初期。该阶段的钢筋混凝土属于初始发展阶段,因此各项指标都比较低,尤其是强度等指标。第二阶段,从20世纪初期到第二次世界大战前后。随着社会的发展和对建筑的需求,技术人员根据极限平衡理论,提出了“塑性内力重分布计算方法”,推动了钢筋混凝土的发展。第三阶段,从二战后到现在。由于计算理论、设备和技术的发展,钢筋混凝土的各项性能较好,主要用于高层建筑、大跨桥梁等重要建筑结构中,计算理论上采用充分考虑混凝土和钢筋塑性的极限状态设计理论。
1.2 钢管混凝土的发展和研究
相对于钢筋混凝土,钢管混凝土主要是在成型的理论上开始发展的,国外的研究要比国内早一些,但总体上的差距不大。从国外看,不少国家在20世纪就开始大量的应用钢管混凝土进行建设。例如,1937年苏联列宁格勒采用集束的小直径钢管混凝土作为拱肋,建造了横跨涅瓦河的101 m跨度的下承式拱桥。由于钢管混凝土的高强度等特性,使用范围比较广泛。国内钢管混凝土的应用较晚,20世纪80年代后期,钢管混凝土结构在我国得到了较大发展,科研和工程实践都有较好的开展。
2 ANSYS非线性有限元理论确定材料本构关系
ANSYS软件作为多功能有限元通用分析程序能够更加准确地分析本构关系、构建矩阵等,可以详细地进行钢管混凝土和钢筋混凝土力学性能分析研究。
2.1 混凝土材料破坏准则
混凝土破坏准则是描述混凝土破坏时其应力状态或应变状态满足的条件。目前,ANSYS软件主要采用Willam-Warnke五参数破坏准则来检查混凝土开裂和压碎的参数。利用此破坏准则可将混凝土的破坏模型分为以下三种类型:由于压力而导致的压碎性破坏、由于竖直剪切力而发生开裂、由于拉力而导致的开裂破坏。
2.2 混凝土的本构关系
混凝土的抗拉强度较差,其在受拉情况下开裂前后的本构关系差异较大。
(1)开裂前混凝土的本构关系。
由于组成混凝土的材料具有复杂性,在混凝土开裂前,其各种特性都未发生变化,利用ANSYS构建混凝土的本构矩阵可以表示为:

(2)开裂后混凝土的本构关系。
混凝土开裂后混凝土的抗剪切力、应力应变等都会发生变化。此时,利用ANSYS来构建混凝土的本构矩阵可以表示为:

(3)混凝土受压情况下的本构关系。
因为ANSYS采用“弹塑本构+压碎模型”来分析混凝土受压情况下的本构关系,所以混凝土弹塑性本构矩阵表达式分析应以屈服准则、流动法则以及硬化法则为基础,准确、合理、规范地进行弹塑性本构矩阵表达式计算。
首先,已知盈利空间中屈服条件表示为空间曲面,即

对式(1)两边进行微分处理,得到函数
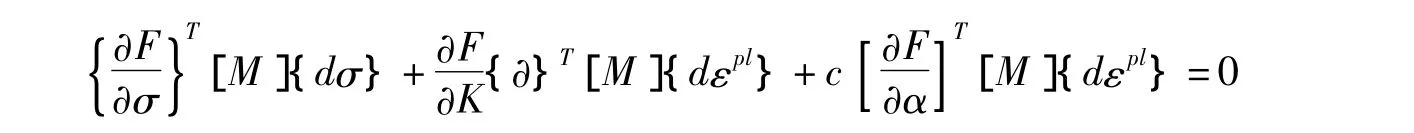
其次,增量理论中对于弹性增量和塑性增量的说明,用函数表示为:

再结合虎克定律,弹性应变增量与应变增量的关系用函数表示为:

通过以上公式可以得到塑性应变增量,用函数表示为:

将以上式(3)、式(4)代入式(2),得到的函数为:

再将式(5)两侧分别乘以[D]并移项,得到

将式(6)代入式(3),得到的函数为:
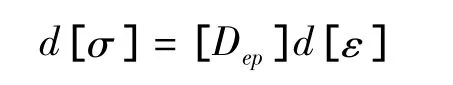
此函数即为弹塑本构关系矩阵。
3 钢管混凝土和钢筋混凝土力学性能比较
钢管混凝土和钢筋混凝土的力学性能探究,主要是对比钢管混凝土柱和钢筋混凝土柱轴心受压力学性能、钢管混凝土柱和钢筋混凝土柱偏心受压力学性能,以此来深入地了解钢管混凝土力学性能。
3.1 钢管混凝土柱和钢筋混凝土柱轴心受压力学性能比较
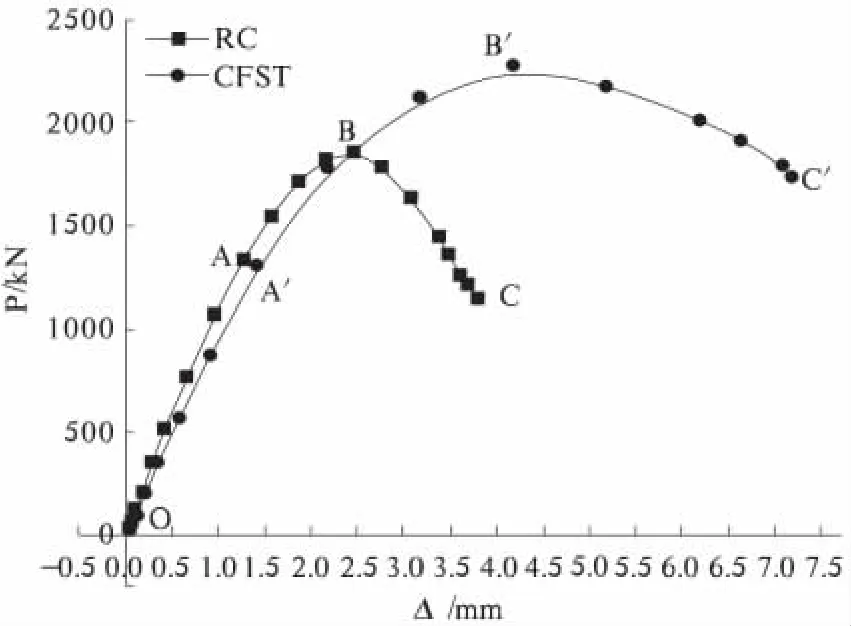
图1 钢筋混凝土柱和钢管混凝土柱受轴心压力作用下的曲线变化比较
钢管混凝土柱轴心受压时其核心混凝土的受力特点是:侧压力是被动的,且随纵向压应力的增大而增大。随着混凝土应力的增加,钢管混凝土柱的纵向形变系数也会随之增加,达到一定程度时,混凝土体积膨胀到极限,钢管就会发生形变,使其遭到破坏。
3.1.1 破坏过程分析
(1)破坏模式比较。钢筋混凝土的研究资料表明,钢筋混凝土柱破坏是出现混凝土压碎脱落现象,钢筋混凝土柱内部破坏程度较大。对于钢管混凝土柱,其破坏时也会出现混凝土压碎现象,但由于核心混凝土开裂压碎产生体积膨胀而侧向压迫钢管屈曲外鼓破坏。
(2)轴压过程比较。两种柱在轴压作用下所产生的破坏过程主要有两个阶段。第一阶段,轴压力最小,钢筋混凝土柱在轴压力作用下,其变形增加,但轴力变化较小,相应的曲线变化较小,而钢管混凝土在较小轴压力作用下,其钢管受压程度较小,还具有很大的弹性空间。第二阶段,随着轴压力的增大,钢筋与混凝土之间的粘结力下降,钢筋混凝土柱的混凝土开始脱落,钢筋受轴压力的作用,弹性逐渐增大,直到达到弹性最大值,钢筋被破坏。而随着轴压力的增加,钢管混凝土柱进入弹塑阶段,其核心混凝土受压出现碎裂,但因此产生的体积膨胀可以缓解钢管受压程度,使得钢管抗压强度增加,钢管虽有一定的屈曲,但没有钢筋混凝土弯曲程度大(见图1)。钢管混凝土性能要比钢筋混凝土性能更加优越,轴压过程充分表明,钢管混凝土具有较高的抗压能力和较大的变形能力。
3.1.2 机理比较
结合图1,可以看出混凝土在钢管的约束下,核心混凝土的强度和抗变形能力增加,使钢管混凝土柱具有良好的延性,能够增加钢管混凝土柱抵抗能力。而钢筋混凝土是因钢筋与混凝土之间的粘结力才结合到一起的,一旦外力破坏了粘结力,钢筋混凝土就会受到严重的破坏。由此可见,钢管混凝土在很多方面,均优于钢筋混凝土,并且可以在较多的工程中应用,尤其是高层、大跨度桥梁等一些大型工程。
3.2 钢管混凝土柱和钢筋混凝土柱偏心受压力学性能比较
3.2.1 建立有限元模型
对于偏压下钢管混凝土柱和钢筋混凝土柱有限元模型的构建主要是结合两类柱的相关参数建立的。钢管混凝土柱和钢筋混凝土柱的有限元模型如图2、图3所示。
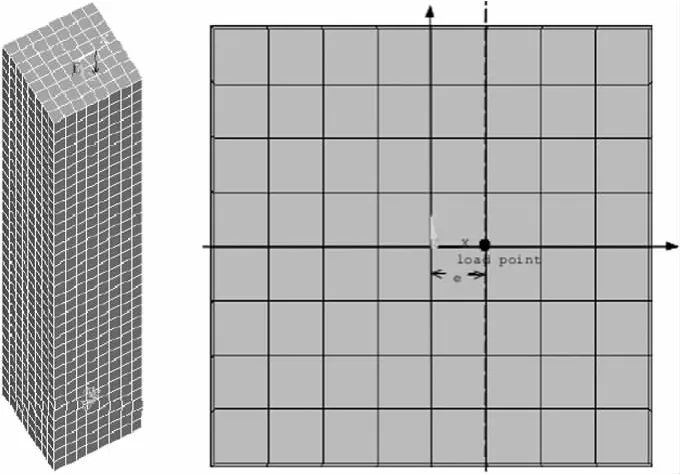
图2 偏压下钢管混凝土柱的有限元模型
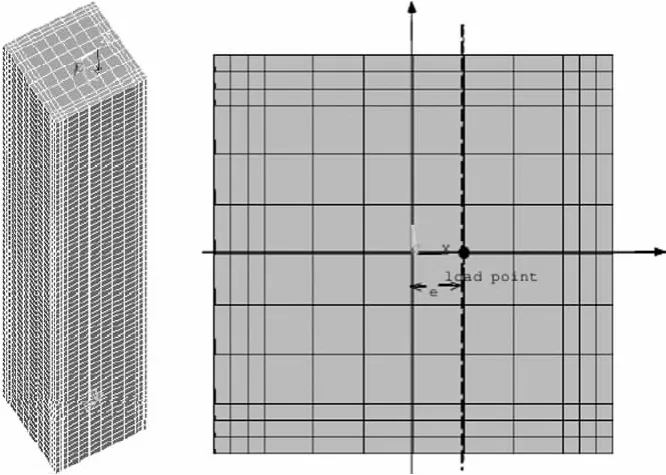
图3 偏压下钢筋混凝土的有限元模型
3.2.2 偏压下钢管混凝土柱和钢筋混凝土柱的破坏过程比较
利用有限元分析法可以得到关于钢管混凝土柱和钢筋混凝土柱的荷载—挠度曲线图(见图4)。
从图4中可以看出偏压下钢管混凝土柱和钢筋混凝土柱在弹性阶段,荷载—挠度相同,曲线无变化,两者进入弹塑阶段后,因偏心压力增大,钢筋混凝土柱受压一侧很快达到屈服极限,而钢管混凝土则可继续承载而推迟达到屈服极限的时间,显示出较高的承载力和耐受变形的能力。随着偏心压力的作用,在破坏阶段,钢筋混凝土完全被破坏,而钢管混凝土核心混凝土成为约束混凝土,其强度有较大提高,同时其在破坏中所产生体积变化可以缓解钢管受压,进而延迟了钢管的破坏时间,提高了承载力和抵抗变形的能力。
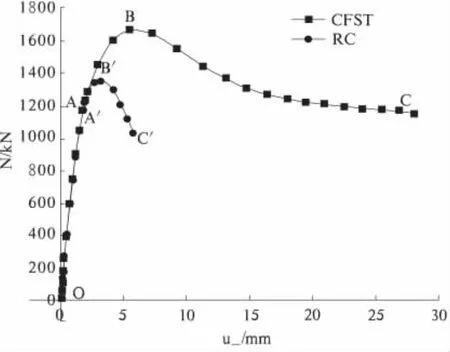
图4 偏压下钢管混凝土柱和钢筋混凝土柱的荷载—挠度曲线
4 结束语
从钢管混凝土和钢筋混凝土受力情况下力学性能比较来看,钢管混凝土的力学性能优于钢筋混凝土的力学性能。将其合理、有效、规范地应用于建筑工程中,可以有效地解决高层、超高层、大跨度结构问题,从而创造出更多新的结构形式。
[1] 卢明奇,杨庆山.矩形钢管混凝土柱力学性能非线性有限元分析[J].沈阳工业大学学报,2012(2):224-230.
[2] 杜闯,戎贤,乔金丽,等.钢管混凝土柱抗震性能比较[J].土木工程学报,2012(S1):107-111.
[3] 齐甦,明磊.钢管高强膨胀混凝土轴压短柱试验研究[J].混凝土,2010(2):53-56.
[4] 尧国皇,李永进,廖飞宇.钢管混凝土叠合柱轴压性能研究[J].建筑结构学报,2013(5):114-121.
[5] 谷利雄,丁发兴,付磊,等.圆端形钢管混凝土轴压短柱受力性能研究[J].中国公路学报,2014(1):57-63.
[6] 祝雯.钢管混凝土结构的研究现状及发展趋势[J].广州建筑,2011(1):3-8.
[7] 杨政,侯健,邱明星.钢筋混凝土短柱轴心受压承载力分析[J].建筑结构,2011(S2):150-155.
[8] 王芳,查晓雄.钢管珊瑚混凝土试验和理论研究[J].建筑结构学报,2013(S1):288-293.
