寒区矿山高陡边坡稳定性影响因素的敏感性分析

范新宇，罗学东，李津玮，李 旋，梅年峰

(1.中国地质大学(武汉)工程学院，武汉 430074;2.中国电建顾问集团西北勘测设计研究院，西安 710065)

1 研究背景

矿山边坡的变形破坏是多因素协同作用的结果，边坡系统的复杂性、非线性和可变性使得常规的单因素敏感性分析难以得到合理的结果，寻找一种能够描述边坡不确定性问题的分析方法显得尤为重要［1］。灰色系统理论可以通过对各影响因素的不完备信息进行分析，找出其内在关联性，由关联系数的大小对各因素影响程度进行排序［2］，均匀设计的优点在于不仅可以使影响因素进行交互作用，还可减少数据处理过程中试验次数和计算工作量［3］，两者综合应用可实现对边坡稳定性影响因素的多重组合分析。

在边坡稳定性影响因素敏感性分析方面，许多专家学者做过大量研究，如文献［4－5］中，选取了重度、内摩擦角、黏聚力、坡角、地震加速度等5个因素进行均匀试验，并利用灰色理论对边坡敏感性进行分析，结果显示黏聚力是最主要的影响因素;文献［6］选取重度、黏聚力、内摩擦角、坡角及坡高5个因素进行均匀试验设计，通过灰色关联分析，发现抗剪强度指标是影响土质边坡稳定性的最重要的因素。但不同自然环境下的边坡失稳影响因素不尽相同，对于寒区边坡，以往的研究大多集中在数据处理和关联度的分析上，对影响寒区边坡稳定性的相关因素却鲜有系统的分析。本文综合考虑了寒区环境下冻融循环作用及爆破振动效应对边坡稳定性的影响，在室内冻融试验和现场爆破振动测试基础上，引入了冻融系数和爆破损伤因子作为相关因素变量，将岩体的稳定性系数作为系统特征变量，建立了相关因素变量与系统特征变量之间的灰色关系，同时，基于均匀设计将各影响因素进行了交互试验，对试验结果进行灰关联分析，依据关联度的大小确定影响边坡稳定的主次因素。

2 灰关联模型的建立

假设影响边坡稳定的因素有n个，将影响边坡稳定的n个变量集中包含在集合X中，相应的边坡稳定性系数用集合Y表示，通常将集合X作为子数列，Y为母数列。数列X，Y可用下列矩阵形式表示:

2.1 数据的预处理

各数列中的参数由于无统一的量纲和单位，因此数据无可比性。为了便于分析，同时消除量纲和数级因素的影响，须对参数进行标准化处理，最终变为同一数量级的无量纲数据，具体处理方法为［7］

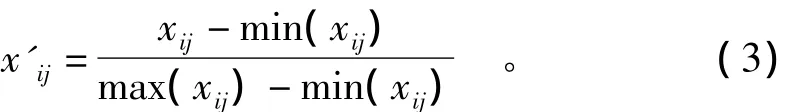
式中:x'ij为序列处理后的数据;xij为初始数据;max(xij)为数据序列中的最大值;min(xij)为数据序列中的最小值。

2.2 关联度分析

给定实数 γ(yij，xij)，若实数 γ(Yij，Xi)=满足规范性、整体性、偶对称性，且随的减小而逐渐增大，则γ(yij，xij)为Xi对Yi在j点的关联系数，具体求解过程为:

设一矩阵Δij有如下关系:

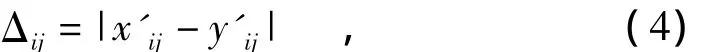
|Δij|的最大值和最小值可表示为

则Xi对Yi在k点的关联系数可表示为

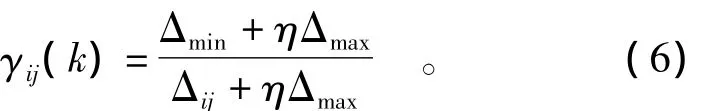
其中，η为分辨系数，一般取0.5。

Xi对Yi关联度可以表示为

式中rij为Xi对Yi的关联度，关联度数值越大，说明该因素对边坡稳定性影响越大，反之影响程度越小。

3 均匀设计数值试验

均匀设计可以将数值点均匀地分布在试验范围内，使得能用较少的点获取较多的信息，尤其适用于多因素、多水平的试验［8］，对复杂的不确定性问题有较好的解决能力，该特点使其适用于非线性的岩土问题分析［9］。

3.1 均匀试验设计

均匀设计是在正交设计的基础上，根据数论在多维数值积分中的应用原理而实现的［10］，序列构造可以通过查询均匀设计表来获取，其中每个设计表中包含2组不同的设计类型，分别记作Un(qs)和(qs)，式中n为设计试验次数，q为变量取值范围内均匀分段的个数，s为列的个数。2种均匀设计类型存在差别，为了防止n为非素数时序列结构中不存在n－1列，故将Un去掉最后一行来构造，因此较Un更具均匀性，在应用时应优先选取［5］。

3.2 试验因素及范围的选取

蒙库露天铁矿位于新疆高海拔、高寒地区，平均昼夜温差15～20℃，采用爆破方式进行开挖，这2种因素持久地作用在岩体上，会对岩体力学性能造成一定的损伤，因此在进行边坡稳定性影响因素分析时，爆破因素和冻融循环效应是不可忽略的。在综合分析矿区岩体结构、岩性、边坡几何形态、冻融效应及爆破振动作用基础上，综合确定坡高(H)、坡角(β)、重度(γ)、黏聚力(c)、内摩擦角(φ)、弹性模量(E)、冻融系数(η)、爆破损伤因子(D)8个因素作为影响该边坡稳定性的可能因素。

在计算上述岩体力学参数时，难点在于如何引入冻融系数(η)和爆破损伤因子(D)量化值并将其应用到边坡稳定性分析当中。本文通过室内冻融循环试验得到岩块在一定冻融循环次数下的冻融系数，文献［11］所建立的TSMR地质分类方法考虑了冻融作用对岩体的影响，引入了岩石的冻融系数来量化岩体质量，因此利用文献［11］的方法得到考虑冻融作用的岩体质量量化值;在矿区现场爆破振动测试基础上，利用文献［12］所述方法，以岩体声速降低率表征爆破损伤因子D，最终通过广义Hoek－Brown准则将两者量化值引入到岩体力学参数的选取中。用这种方法获得的c，φ，E的值都考虑了η和D的影响，利用这些参数对边坡稳定性进行分析时，也能充分考虑冻融和爆破作用的影响。通过计算，各因素的取值范围如表1所示。

表1 参数取值范围Table 1 Ranges of parameter value

3.3 均匀设计的计算

能否准确利用均匀设计方法对数据展开交互试验，关键在于合理选择均匀设计表，而均匀设计表是根据因素的数量及各因素的水平值综合确定的［6］。本文共有8个因素参数，且参数水平值范围较大，根据实际情况，拟采用均匀设计表U*10(108)进行均匀试验。基于均匀分散的原则，将每个因素分为10个水平数，均匀设计表如表2所示，其中，第1行表示8组因素的编号，第1列为各因素的水平编号，表中其余数字为各因素的水平值编号。

表2 均匀设计表(108)Table 2 Uniform design table(108)

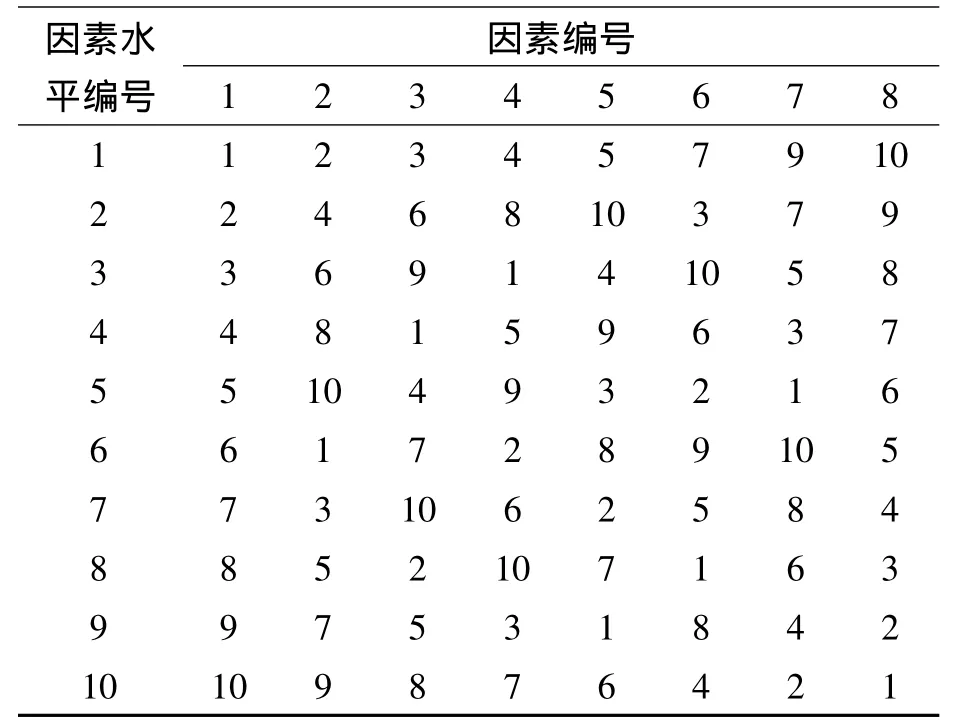
表2 均匀设计表(108)Table 2 Uniform design table(108)

?

均匀设计表的本质是将因素的取值范围分为不同的水平数，并按照一定方式将各因素的水平值重新排列，构建起新的数据组合序列，大大减少计算步骤。参照文献［6］中各因素的位级变化范围，将每个因素划分为10个水平级数，利用表2的排序方式对各因素的水平数值进行排列交互，构建起因素间新的数据组合序列，各因素水平值的排列结果如表3中因素指标所示。

判断各影响因素对边坡稳定性的影响程度，需要构建起评价指标，稳定性系数(Fs)是定量评价边坡稳定性的指标，故采用Fs作为交互试验的评价指标。基于表3中因素指标参数，利用数值计算软件分别计算出不同组合类型下边坡稳定性系数Fs的数值，算得的边坡稳定性系数如表3所示。

4 均匀试验结果的灰关联分析

表3建立起了边坡稳定性影响因素和评价指标之间的关系，在进行灰关联分析时，将反映边坡稳定性的评价指标定义为灰关联模型的系统特征变量(母序列)，将边坡稳定性的影响因素指标定义为相关变量(子序列)，从而建立起子序列与母序列的灰色关联模型。

由于上述因素指标的单位不一致，直接计算会造成较大误差，为消除单位不同所造成的误差，需对样本数据序列进行无量纲化处理，使其变为统一的无量纲数据。标准化处理后的数据如表4所示，按式(4)至式(7)的计算方法对标准化处理后的数据进行关联度分析，算得影响因素对边坡稳定性系数的关联度如表5所示。

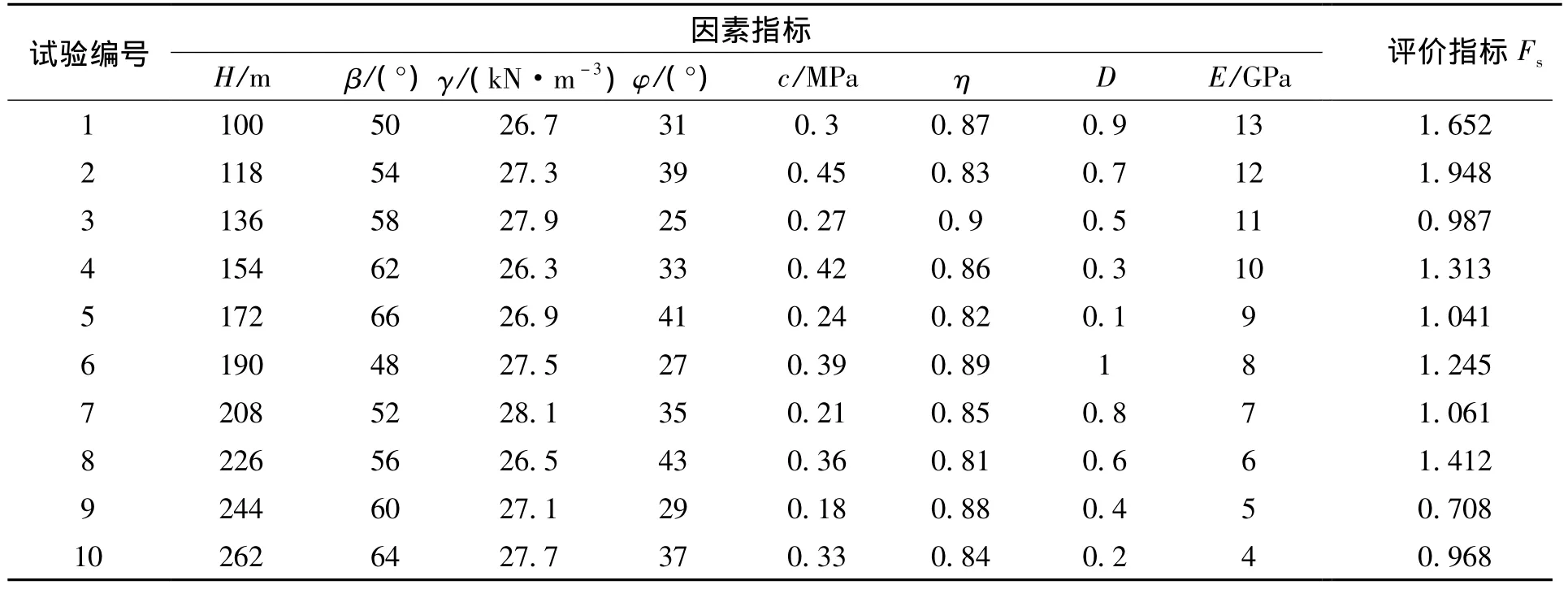
表3 均匀设计计算结果Table 3 Calculation results of uniform design

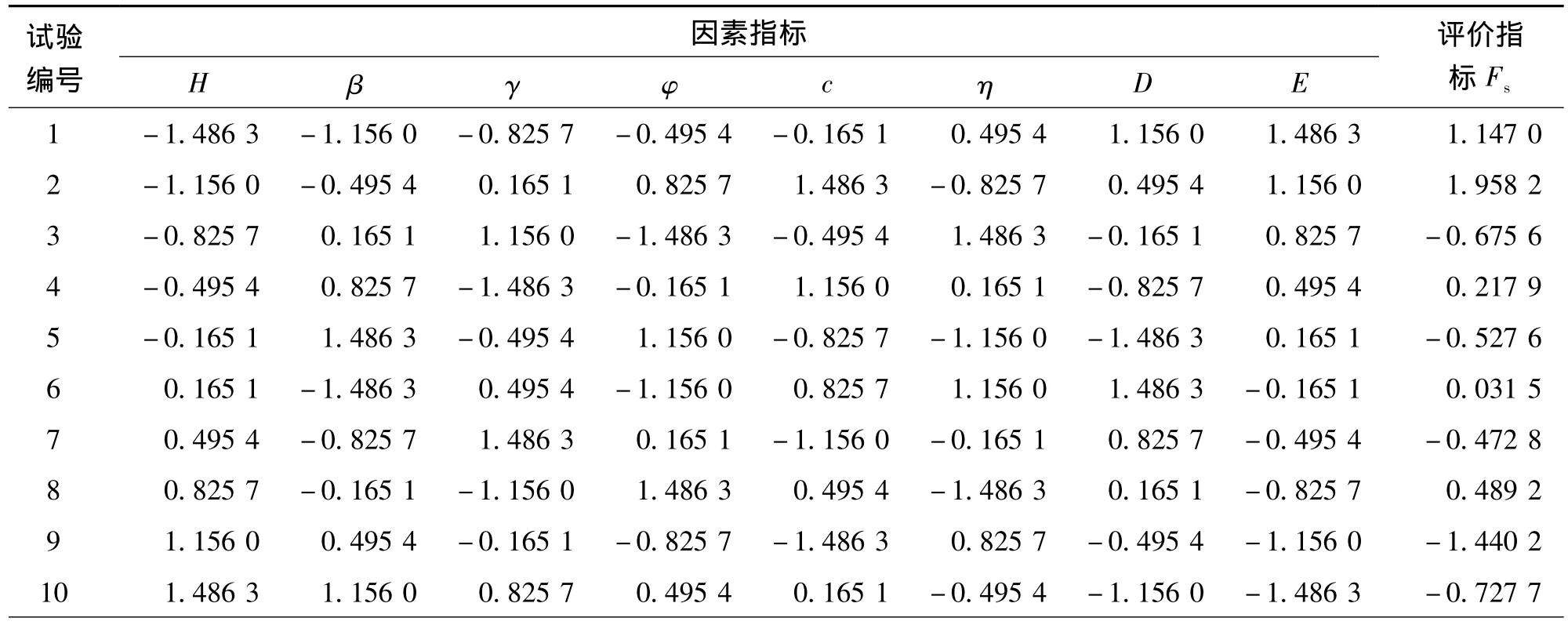
表4 数据的标准化处理Table 4 Standardized processing of data

表5 关联度计算结果Table 5 Calculation results of correlation degree

表5中的系数即为边坡稳定性影响因素与稳定性系数之间的关联度系数，针对本寒区边坡工程，各因素对边坡稳定性系数的关联度大小依次为:黏聚力＞弹性模量＞爆破损伤因子＞冻融系数＞坡高＞内摩擦角＞重度＞坡角。表明控制岩质边坡变形破坏的主要因素为岩体自身强度因素，但爆破振动产生的振动效应对边坡稳定也有很大影响，此外，寒区边坡由于特殊的地理环境因素，冻融作用导致的岩体劣化也是影响边坡稳定性的主要因素之一。

5 结论

(1)针对寒区矿山边坡开挖方式和特殊环境因素，在常规边坡稳定性影响因素基础上，引入了冻融系数(η)和爆破损伤因子(D)作为寒区边坡稳定性影响因素，可为寒区矿山边坡敏感性分析提供重要参考;

(2)针对传统分析方法的不足，本文综合运用均匀设计和灰关联理论对影响因素的敏感性进行分析。将影响边坡稳定性的各因素作为子序列，稳定性系数作为母序列，基于均匀设计对各影响因素进行交互试验，利用灰关联理论对试验结果进行分析，构建起基于均匀设计的灰关联分析法。

(3)通过灰关联分析可知，影响边坡稳定的4个重要因素依次为:黏聚力、弹性模量、爆破损伤因子及冻融系数，说明对边坡稳定性影响最大的为岩体自身强度因素，但爆破振动和冻融循环作用对边坡稳定性的影响不可忽视。本文方法可为寒区边坡监测或治理提供参考。

［1］汪 洋，殷坤龙，安关峰.滑坡敏感因子的灰色关联分析［J］.岩土力学，2004，25(1):91－93.(WANG Yang，YIN Kun-long，AN Guan-feng.Grey Correlation Analysis of Sensitive Factors of Landslide［J］.Rock and Soil Mechanics，2004，25(1):91－93.(in Chinese))

［2］邓聚龙.灰色系统基本方法［M］.武汉:华中理工大学出版社，1987.(DENG Ju-long.Basic Method of Grey System［M］.Wuhan:Huazhong Institute of Technology Press，1987.(in Chinese))

［3］王兆军.均匀设计在参数设计中的应用［J］.南开大学学报(自然科学版)，2000，33(2):57－60.(WANG Zhao-jun.The Application of Uniform Design in Parameter Design［J］.Acta Scientiarum Naturallum(Universitatis Nakaiensis)，2000，33(2):57－60.(in Chinese))

［4］陈高峰，卢应发，程圣国，等.基于均匀设计的边坡敏感性灰色关联分析［J］.灾害与防治工程，2008，64(1):1－6.(CHEN Gao-feng，LU Ying-fa，CHENG Sheng-guo，et al.Grey Correlation Analysis of Slope Stability Sensitivity Based on Uniform Design［J］.Disaster and Control Engineering，2008，64(1):1－ 6.(in Chinese))

［5］陈高峰，程圣国，卢应发，等.基于均匀设计的边坡稳定性敏感性分析［J］.水利学报，2007，37(11):1397－ 1401.(CHEN Gao-feng，CHENG Sheng-guo，LU Ying-fa，et al.Sensitivity Analysis of Slope Stability Based on Uniform Design［J］.Journal of Hydraulic Engineering，2007，37(11):1397－1401.(in Chinese))

［6］井培登，范付松，宋义亮，等.基于均匀设计的边坡敏感性灰色关联分析［J］.安全与环境工程，2011，18(2):116－118.(JING Pei-deng，FAN Fu-song，SONG Yi-liang，et al.Grey Correlation Analysis of Slope Sensitivity Based on Uniform Design［J］.Safety and Environmental Engineering，2011，18(2):116－ 118.(in Chinese))

［7］黄建文，李建林，周宜红.基于 AHP的模糊评判法在边坡稳定性评价中的应用［J］.岩石力学与工程学报，2007，26(增刊 1):2627－2632.(HUANG Jian-wen，LI Jian-lin，ZHOU Yi-hong.Application of Fuzzy Analysis Based on AHP to Slope Stability Evaluation［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26(Sup.1):2627－2632.(in Chinese))

［8］方开泰.均匀设计与均匀设计表［M］.北京:科学出版社，1994.(FANG Kai-tai.Uniform Design and Uniform Design Table［M］.Beijing:Science Press，1994.(in Chinese))

［9］梅松华，盛 谦，冯夏庭.均匀设计在岩土工程中的应用［J］.岩石力学与工程学报，2004，23(16):2694－2697.(MEI Song-hua，SHENG Qian，FENG Xia-ting.Application of Uniform Design to Geotechnical Engineering［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(16):2694－2697.(in Chinese))

［10］杨 静，陈剑平，王吉亮.均匀设计与灰色理论在边坡稳定性分析中的应用［J］.吉林大学学报(地球科学版).2008，38(4):654－658.(YANG Jing，CHEN Jian-ping，WANG Ji-liang.Application of Uniform Design and Grey Theory in Analysis of Slope Stability［J］.Journal of Jilin University(Earth Science Edition)，2008，38(4):654－658.(in Chinese))

［11］张元才，黄润秋，赵立东，等.天山公路边坡岩体质量评价TSMR体系研究［J］.岩石力学与工程学报，2010，29(3):617－ 623.(ZHANG Yuan-cai，HUANG Run-qiu，ZHAO Li-dong，et al.Study of Tianshan Slope Rock Mass Rating(TSMR)System［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(3):617－623.(in Chinese))

［12］闫长斌，李国权，陈东亮，等.基于岩体爆破累积损伤效应的 Hoek-Brown准则修正公式［J］.岩土力学，2011，32(10):2951－2956.(YAN Chang-bin，LI Guoquan，CHEN Dong-liang，et al.Amended Expressions of Hoek-Brown Criterion Based on Blasting Cumulative Damage Effects of Rock Mass［J］.Rock and Soil Mechanics，2011，32(10):2951－2956.(in Chinese))