金属橡胶非线性隔振器试验研究与参数分析

李玉龙,白鸿柏,何忠波,路纯红

(1.军械工程学院 车辆与电气工程系车辆工程教研室，石家庄 050003；2.军械工程学院 车辆与电气工程系，石家庄 050003)

金属橡胶非线性隔振器试验研究与参数分析

李玉龙1,白鸿柏1,何忠波2,路纯红1

(1.军械工程学院 车辆与电气工程系车辆工程教研室，石家庄 050003；2.军械工程学院 车辆与电气工程系，石家庄 050003)

研究了变激励条件下金属橡胶非线性隔振器的参数变化。以某型隔振器为研究对象，对其进行了静态试验及不同正弦激励条件下动态试验。借助双折线泛函本构关系的本构模型，利用粒子群优化算法对不同激励条件下的隔振器模型参数进行了识别，通过识别参数的对比得到了隔振器各参数在不同激励情况下的变化趋势。结果显示对金属橡胶非线性隔振系统进行动力学分析时，必须首先对实际工况下隔振器进行动态试验。再通过参数识别获取隔振器准确的数学模型，才能对金属橡胶隔振系统进行准确的动力学分析。为金属橡胶隔振系统的动力学分析提供了一般方法。

振动与波；金属橡胶隔振器；动力学模型；粒子群优化算法；参数识别

金属橡胶是一种经特殊工艺将一定质量的、拉伸开的、螺旋状态的金属丝有序地排放在冲压或碾压模具中，通过冲压或碾压成型的方法制成的弹性多孔金属材料。其内部有很多孔洞，既呈现类似橡胶材料的弹性和阻尼性能，同时又保持金属的优异特性，故称其为金属橡胶(Metal Rubber)。其金属特性使其具有耐高温、高压、高真空、超低温的特点，且在空间环境下不挥发，不怕辐射和粒子的撞击，采用耐腐蚀的金属丝还可以工作在腐蚀环境中，不产生老化现象，是一种具有重要工程应用价值的新兴材料，已被广泛应用于航空航天、汽车、船舰等工业领域，对提高设备的寿命、可靠性都有较大的优势[1]。

金属橡胶材料制成隔振器的恢复力不仅和系统的瞬时变形状态有关，还与系统的变形历史有关，具有明显的迟滞非线性特性，这一特点能拓宽其在许多特殊工程领域的应用。但由于它具有突出的结构非线性、几何非线性、材料非线性等因素和明显的迟滞非线性效应，其动力学建模与理论分析就相对复杂，已成为目前金属橡胶研究的难点和热点问题[2-8]。

本文对为某大型装备设计的某型金属橡胶隔振器进行静动态实验研究，拟应用隔振器的双折线泛函本构关系的数学模型，确定模型各参数的明确物理意义；再通过试验数据用粒子群算法对模型的各参数进行优化识别；最后，对比相同幅值不同频率、相同频率不同幅值下动态数据辨识的参数，得到金属橡胶隔振系统动力学特性随激励频率和幅值变化的一般规律，为金属橡胶隔振系统的动力学分析与研究提供了一般方法。

1 金属橡胶隔振器的静、动态试验研究

1.1 金属橡胶隔振器结构及静态试验研究

常用的单向金属橡胶隔振器结构及制备的金属橡胶隔振元件如图1所示，采用上下两块金属橡胶元件并联组合使用。由于金属橡胶材料的拉压性能具有较大的差异，单块金属橡胶元件预压装配使用显现出明显的非对称弹性，且由于粘性阻尼力及双折线恢复力的影响，更容易引起隔振器力学性能的不稳定[6,7]，使隔振器难以得到预定的动力学性能，甚至使隔振系统动力学分析无法进行。图1所示的隔振器结构若保证制备的上下两块隔振元件性能一致，使金属橡胶隔振器具有在整体上的拉压一致性，从而获得稳定的隔振性能。

图1 金属橡胶隔振器

根据指标要求设计相应的金属橡胶元件，确定金属丝经、螺旋卷直径、用料质量、成型压力等参数，并将制备的八个金属橡胶元件组装成隔振器（共四件），用WDW-T200微机控制电子万能试验对隔振器进行静态加载，如图2所示，测试得到隔振器的力—位移曲线如图3所示。

图2 静态实验示意图

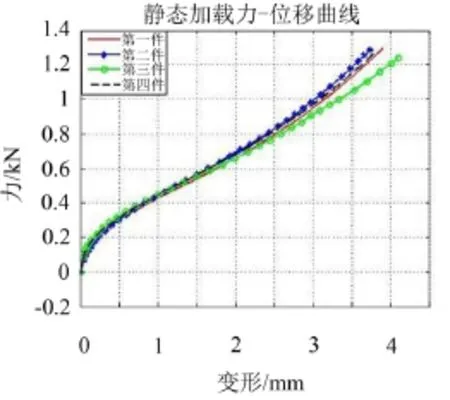
图3 静态试验结果

由图3可知，制备的四件隔振器的力—位移曲线基本一致，说明本文设计的该隔振器重复制备的各件能保持较好的一致性。从曲线的走势看，隔振器的力—位移曲线并非为单一斜率的直线，而是有明显的弯曲，证明隔振器呈现非线性性能，且在小变形（0 mm～0.5 mm）范围内，呈现曲线的斜率（隔振器的刚度）随着变形量的增大逐渐减小，显示隔振器的渐软特性；在变形为0.5 mm～1.5 mm范围内，斜率基本保持不变，刚度不变；在较大的变形范围内（变形大于1.5 mm），斜率随着变形的增大而逐渐增大，呈现渐硬特性。可见该金属橡胶隔振器力学性能的复杂性，需要进行进一步的动态实验研究，以了解其动力学性能。

1.2 金属橡胶隔振器动态试验研究

本节对隔振器进行动态的正弦加载试验，由PLS-20电液伺服疲劳试验机和DH 5936振动测试系统组成的动态试验系统进行，如图4所示。

图4 动态试验示意图

分别加载相同频率（1 Hz）不同幅值（1 mm、2 mm、3 mm、4 mm）和相同幅值（1 mm）不同频率（5Hz、10 Hz、15 Hz、20 Hz）的正弦激励，测试隔振器的力—位移曲线，实验结果曲线如图5所示。

图5 不同频率与幅值加载下迟滞环

从图5可以看出，在正弦加载的动态试验中，改变频率和幅值，迟滞环（动态力—位移曲线）都有较为明显的变化，证明加载条件的改变能够会导致隔振器力-位移关系的变化。从图5还可以看出，试验得到的迟滞回线并不是关于横轴（力的零平衡位置）严格对称的，这主要是由于试验过程中，传感器引入了初始偏移量，导致数据存在一定的平移，在使用试验数据时，必须根据数据平衡位置进行平移，使数据关于坐标轴严格对称，以补偿传感器引入的偏差。而且，由于设备控制精度的问题，在改变频率的加载中，频率增大增加了设备的控制难度，设定的1 mm的振幅随着频率的增大，实际的激励振幅有所减小，在下面的分析中应予以考虑。但是，从试验结果曲线可以看出，在设计金属橡胶隔振器时，必须考虑到隔振器的实际工作工况，掌握其工作情况下振动幅度及振动频率，才能得到满意的隔振效果。

2 双折线泛函本构关系隔振器模型

为研究振动激励环境对隔振器的影响情况，需要首先对隔振器建立准确的模型，并对模型参数在各种激励状态下进行辨识，以研究激励变化对隔振器各参数的影响情况。为建立隔振器的准确模型，并为其非线性动力学分析提供准确可靠的依据。

非线性隔振器的数学模型有很多种，具有代表性的有干摩擦理想模型、双折线模型、Davidenkov模型、Bouc-Wen模型、迹法模型[2]，还有学者提出了广义恢复力模型[9]，这些模型都可以描述非线性迟滞振动系统的数学模型，大都是针对不同的迟滞弹性材料或元件而提出的，它们各有不同的应用场合，并有各自不同的优缺点。

由于双折线模型能很好地描述系统出现干摩擦时的情形，且形式简单，需要辨识的物理参数少，各参数物理意义明确，且能准确的表示金属橡胶的动态力—位移关系。因此，该模型的应用范围比较广泛，可近似描述金属橡胶、钢丝绳、MRF等多种材料的滞后非线性，常用于滞后非线性系统的动力学建模与分析等理论研究[10-15]。因此许多专家学者都对金属橡胶隔振器的建模采用双折线本构模型进行分析。本文也借鉴前人的成果采用双折线模型来描述金属橡胶隔振器的性能。其本构关系为

式(1)中x(t)和x˙(t)分别表示隔振器的变形和变形速度，k1为一次线性刚度系数，k3为三次非线性刚度系数，c1为等效粘弹阻尼系数，它们形成与位移有关的弹性力和与速度有关的粘性阻尼力，通常被认为是无记忆恢复力；z(t)是金属橡胶变形过程中干摩擦引起的记忆恢复力，由于该记忆恢复力的存在，金属橡胶隔振系统一般表现出明显的滞后非线性性能，其中zs表示滑移极限，ks表示滑移刚度，且有ks=zs/xs。将记忆恢复力用双折线模型表示[10,13,15]，如图6所示。

图6 双折线迟滞关系模型

图6所示的双折线本构关系是分段单值函数，每一单值支的Fourier级数在支的分叉点收敛于z (t)=0，不能很好的逼近本构关系。胡海岩[15]等人构建了增量方程，周期延拓后用Fourier级数展开，得到记忆恢复力环节表达式为

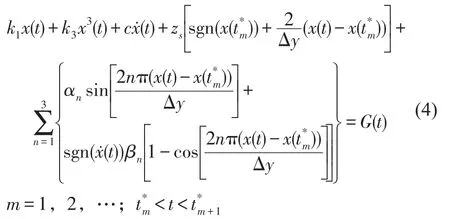
通过不同的参数(k1、k3、c1、zs、αn、βn)组合，双折线模型就能够表示对应任意形状的迟滞环。以表达正弦位移加载下金属橡胶隔振器的动态力—位移性能。

3 隔振器参数优化识别

3.1 参数识别方程

对于隔振器的正弦加载动态实验，其简化模型如图7所示。

图7 隔振器动态加载模型

图7中，激励x(t)=Acosωt，ω为激励频率，A为激励幅值，在刚性基础上隔振器的变形量等于x(t)，可以测得隔振器的恢复力F(t)，则该隔振系统的动力学微分方程为

通过图4所示的实验装置可以测量得到隔振器的变形与激励力的采样信号Fk,xk(k=1,2,…,N)，并令x*m=x(t*m)，由(4)式可以形成参数识别方程。

这里Fk，xk(k=1，2…N)是在区间内的离散采样值，x˙k可由xk得到。

式(6)转化成矩阵形式

其中η是待识别参数向量

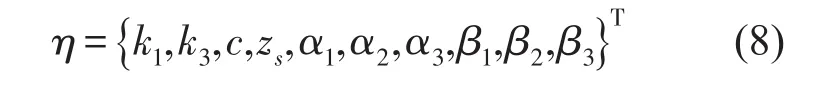
X及F是相应的观测矩阵及向量。

极值的二次代数精度估计为

由上式做出采样历程段的极值估计后可取

先求出待识别参数向量为ηˆ，由(3)式可得到ys的一组估计

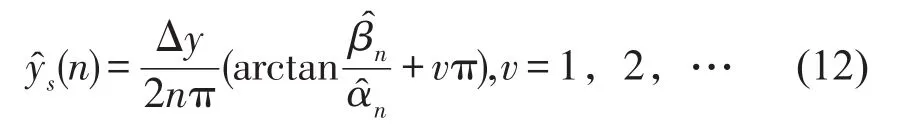
因为间接Fourier展开级数以o(1/n2)的速度收敛，从主成份选择回归变量的角度看，取yˆs为yˆs(1)，即

3.2 基于粒子群算法的隔振器参数优化识别

3.2.1 优化识别算法选取

要识别隔振器的各参数，在实测信号的信噪比比较高时可直接使用最小二乘法获得上述参数向量的无偏估计但测试信号难以避免噪声污染，有时信噪比还比较低，观测阵中的一系列非线性运算将使残差的统计特性变得十分复杂，而且从参数识别方程(6)式可以看出，待识别的参数k1和zs都是关于位移xk的系数（可认为是线性刚度），仅用最小二乘法难以分离准确的结果，但是这两个参数对于准确掌握金属橡胶隔振器的性能至关重要，较大的偏差对隔振器的动力应用会导致严重的预估失策，甚至是重大事故。因此，需要采取更加进化的优化算法进行参数优化识别，有专家用遗传算法对隔振器的参数进行了识别，获得了比较满意的效果[16，17]，但是遗传算法需要进行反复的“交叉”和“变异”操作，辨识过程比较复杂。

随着近年来许多专家对优化算法研究的不断深入，粒子群优化算法(Particle Swarm Optimization，PSO)应运而生。PSO是一种新的进化算法，从随机解出发，通过迭代寻找最优解；通过适应度来评价解的品质；通过追随当前搜索到的最优值，来寻找全局最优。更容易实现，精度高，收敛快，目前已在函数优化、系统辨识、模糊控制等应用领域广泛应用[18]。本节拟采用粒子群算法进行隔振器参数的优化识别。

依据粒子群算法在非线性系统的参数识别中的应用原理，采用实数编码，辨识误差指标取

式中N为测试数据的数量，ηi为模型第i个测试样本输出，为优化识别的参数。

3.2.2 PSO算法的参数设置

1)粒子数：一般选取20～40，对于比较难的问题，粒子数可以取到100～200。

2)最大速度Vmax：决定粒子在一个循环中最大的移动距离，通常小于粒子的范围宽度。较大的Vmax可以保证种群的全局搜索能力，较小的Vmax则保证粒子种群的局部搜索能力加强。

3)学习因子：局部学习因子q1和全局学习因子q2通常设定为2.0，一般全局学习因子取的较大些。

4)惯性权重：一个大的惯性权值有利于展开全局寻优，而一个小的惯性权值有利于局部寻优。当粒子的Vmax很小时，使用接近于1的惯性权重；当Vmax不是很小时，使用权重ω=0.8较好。

还可以使用时变权重。如果在迭代过程中采用线性递减惯性权值，则粒子群算法在开始时具有良好的全局搜索性能，能够迅速定位到接近全局最优点的区域，而在后期具有良好的局部搜索性能，能够精确地得到全局最优解。经验表明，惯性权重采用从0.9线性递减到0.1的策略，会获得比较好的算法性能[17]。

5)中止条件：最大循环数或最小误差要求。

3.2.3 模拟试验

为了验证粒子群算法对本文参数识别结果的正确性，首先取模拟元件的本构方程式(1)，并设其中物理参数为k1=10，k3=1，c=0.1，ks=0.5，zs=0.1，在隔振器初始状态下加载正弦激励，激励为F(t)=2sin(10πt)（激振振幅为2 mm，频率为5 Hz），采样频率为1 000 Hz。运用数值方法对原系统微分方程求解，可得到样本取粒子数为一个激励周期的采样点数200；最大迭代次数为100；采用实数编码，根据设定的各参数值给定寻优范围minη=[0 0 0 0 0 0 0 0 0]，maxη=[100 100 100 100 100 100 100 100 100]；粒子运动最大速度为Vmax=1，速度范围为[-1，1]；学习因子q1=1.3，q2=1.7；采线性递减的惯性权重，惯性权重从0.9线性递减到0.10的策略。

利用上述粒子群算法结合(6)式编程并即可得到待识别的参数，其辨识误差函数J的优化过程如图8所示。

图8 辨识误差函数J的优化过程

从图8可以看出，采用粒子群算法，迭代10步以后辨识误差函数就下降到很小，说明粒子群算法对本文的隔振器参数辨识具有较好的收敛性，且收敛速度快。

再分别用最小二乘算法和遗传算法的参数识别结果与粒子群算法结果进行对比，结果如表1所示。

由表1可知，无噪声干扰时，三种算法均能识别出隔振器的各参数，但是最小二乘算法的识别精度较低；有5%的高斯白噪声干扰时，粒子群算法和遗传算法均能保持较好的识别精度，而最小二乘算法的辨识结果却引入了较大的误差；有噪声和无噪声的识别结果对比还可以发现，粒子群和遗传算法的稳定性较好，噪声对辨识结果的影响不大。但基于粒子群算法的优点，本文采用粒子群算法进行隔振器参数识别，且模拟试验分析表明，粒子群算法识别结果正确可信。

表1 模拟识别结果

3.2.4 试验数据优化识别

利用动态试验实测的数据，可得到样本信号Fk,x˙k,xk。粒子数为一个激励周期的采样点数；最大迭代次数为100；采用实数编码，根据静态试验结果预估各参数值的取值范围，设定寻优范围为minη=[0 0 0 0 0 0 0 0 0]，maxη=[1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000]；粒子运动最大速度为Vmax=1，速度范围为[-1，1]；学习因子q1=1.3，q2=1.7；采线性递减的惯性权重，惯性权重从0.9线性递减到0.10的策略。按照模拟试验相同的识别程序得到各参数辨识结果如表2所示。

根据识别出的参数结合式(6)绘制迟滞回线，可以得到任一组激励条件下识别结果与试验测试结果曲线的对比图，选取任意两组图，如图9所示。

由图9可以看到，用识别出的参数绘制的迟滞回线和试验测试的迟滞回线吻合度很好，再次证明应用粒子群算法优化识别金属橡胶隔振器参数的正确性与有效性。通过表2中的识别参数的结果可得：

1）隔振器的激励条件的变化对隔振器的参数有明显的影响；

2）在低频（1 Hz）激励情况下，随着激励振幅的增大（1 mm～4 mm），隔振器的一次刚度k1、三次刚度k3、等效阻尼c逐渐减小，迟滞恢复力zs逐渐增大；

3）激励幅值保持一定（1 mm），激励频率逐渐增大（5 Hz～20 Hz）隔振器的一次刚度k1、三次刚度k3、等效阻尼c逐渐减小，迟滞恢复力zs基本保持不变；

4)隔振器的刚度渐硬特性和渐软特性的体现是由隔振器的一次刚度k1、三次刚度k3、滑移刚度ks三者之和体现的。

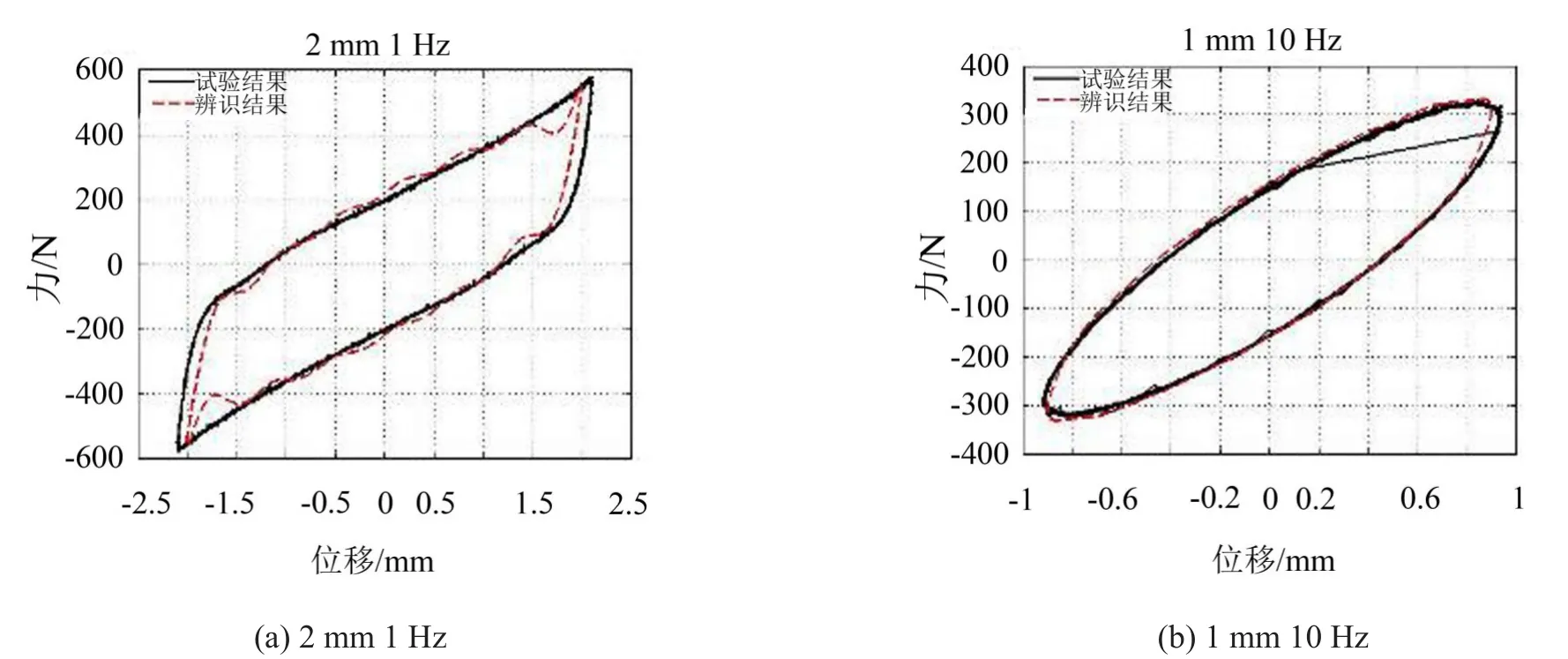
图9 辨识与试验结果对比

因此，通过本文的研究发现，在金属橡胶隔振系统的动力学分析过程中，必须对金属橡胶隔振器在实际工作情况下进行动态加载试验，以确定在该工况下隔振器的各个参数，建立准确的适合该工况下的动力学模型，再进行动力学分析，才能准确的表示系统的动力学性能，否则，动力学分析结果可能产生较大的误差，使动力学分析结果不可信。

4 结语

以某型金属橡胶隔振器为研究对象，进行了静、动态试验测试，绘制了静、动态的力—位移关系曲线。基于双折线泛函本构关系的金属橡胶隔振器数学模型，结合动态试验数据用粒子群算法优化识别了模型的参数。通过模拟识别试验证明了该识别方法的正确性。最后应用该算法识别了同幅值不同频率和相同频率不同幅值正弦激励情况下隔振器的各参数，并进行了对比，得到了激励条件变化对隔振器参数影响的量化的趋势，进而得到了对金属橡胶隔振系统进行动力学分析必须对隔振器进行实际工况下的动态加载试验，以试验获得隔振器的动力学准确参数模型，才能进行系统的动力学分析的结论。

[1]白鸿柏，张培林，郑坚，等.滞迟振动系统及其工程应用[M].北京：科学出版社，2002.

[2]李韶华，杨绍普.滞后非线性模型的研究进展[J].动力学与控制学报，2006，4(1)：8-15.

[3]梅小龙，赵俊生，张保成，等.压缩长度对金属橡胶减振器刚度的影响[J].噪声与振动控制，2013，2(1)：205-207.

[4]Loh CH,Chung ST.A Three-stage identification approach for hysteretic systems[J].Earthquake Engineering and Structural Dynamics,1993,22:129-150.

[5]Yar M,Hammond JK.Parameter estimation for hysteretic systems[J].Journal of Sound and Vibration,1987,117: 161-172.

[6]路纯红，白鸿柏.金属橡胶/橡胶复合叠层耗能器动力学模型及参数识别[J].噪声与振动控制，2007，8(4)：14-18.

[7]路纯红，白鸿柏，辛文彤.非对称弹性粘性阻尼迟滞隔振系统参数识别[J].振动与冲击，2007，26(6)：110-112.

[8]路纯红，白鸿柏.金属橡胶/橡胶复合叠层耗能器的阻尼测试[J].噪声与振动控制，2008，6(3)：152-155.

[9]郝慧荣，白鸿柏，侯军芳，等.金属橡胶广义恢复力模型辨识[J].振动与冲击,2008，27(11)：105-108,202.

[10]李冬伟，白鸿柏，杨建春，等.非线性迟滞系统建模方法[J].机械工程学报，2005，41(10)：205-209+214.

[11]周艳国，屈文忠.金属橡胶非线性动力学特性建模方法研究[J].噪声与振动控制，2013，2(1)：31-36.

[12]闫 辉，姜洪源，刘文剑，A.M.Ulannov.具有迟滞非线性的金属橡胶隔振器参数识别研究[J].物理学报，2009，58(8)：5238-5243.

[13]李冬伟，白鸿柏，杨建春，等.金属橡胶动力学建模及参数识别[J].振动与冲击，2005，24(6)：57-60+138.

[14]张向慧.迟滞非线性系统参数识别方法的研究[J].噪声与振动控制，2001，6(3)：13-16.

[15]胡海岩，李岳峰.具有记忆特性的非线性隔振器参数识别[J].振动工程学报，1989，2(2)：17-26.

[16]李 伟，王珂，德懋，等.基于遗传算法的非线性迟滞系统参数识别[J].振动与冲击，2000，19(1)：8-11.

[17]曾威，于德介.一种基于小生境遗传算法的迟滞非线性系统参数识别方法[J].动力学与控制学报，2004，2(1)：82-85.

[18]刘金琨，沈晓蓉，赵龙.系统辨识理论及MATLAB仿真[M].北京：电子工业出版社，2013.

Experimental Study and ParameterAnalysis of Nonlinear Metal-rubber Isolators

LI Yu-long1,BAI Hong-bai1,HE Zhong-bo2,LU Chun-hong1
(1.Institute of Vehicle Engineering,Ordnance Engineering College,Shijiazhuang 050003,China; 2.Department of Vehicle and Electrical Engineering,Ordnance Engineering College, Shijiazhuang 050003,China)

The parameters change rule of a nonlinear metal-rubber isolator under different incentive conditions was studied.Firstly,both the static experiment and the dynamic experiment under the conditions of different sinusoidal excitations were carried out.On this basis,the bilinear functional constitutive relation model was established.Then,the parameters of the metal-rubber isolator in different incentive conditions were identified by using Particle Swarm Optimization Algorithm.Finally,the parameters change rule of the nonlinear metal-rubber isolator was obtained by comparison of the identification results with the experimental results.It is shown that the dynamic experiment is necessary and the right parameters should be identified under the pertinent incentives before analyzing the nonlinear metal-rubber isolation system.The results of the study may provide a general method for dynamic analysis of the metal-rubber vibration isolation systems.

vibration and wave;metal-rubber isolator;dynamic model;particle swarm optimization algorithm;parameter identification

O328

A

10.3969/j.issn.1006-1335.2015.02.043

1006-1355(2015)02-0194-07

2014－07－30

武器装备“十二五”计划(51312060404)

李玉龙(1986－)，男，河南省杞县人，军械工程学院在读博士生，从事金属橡胶材料研究及应用方面的学习研究。E-mail:556long@163.com