基于PSO-GRNN的直升机旋翼不平衡故障诊断

谢习华，徐 雷，谭 耀，马云荣

（1.中南大学 高性能复杂制造国家重点实验室，长沙 410083；2.山河智能装备股份有限公司 国家级企业技术中心，长沙 410100；3.南方粮油作物协同创新中心，长沙 410100)

基于PSO-GRNN的直升机旋翼不平衡故障诊断

谢习华1,2，3，徐 雷1，谭 耀1，马云荣1

（1.中南大学 高性能复杂制造国家重点实验室，长沙 410083；2.山河智能装备股份有限公司 国家级企业技术中心，长沙 410100；3.南方粮油作物协同创新中心，长沙 410100)

为了准确诊断直升机旋翼不平衡故障，提出了一种基于粒子群算法和广义回归神经网络模型(PSO-GRNN)的故障诊断方法。将交叉验证得到的平均均方误差作为粒子群的适应度函数，运用粒子群算法搜寻最优的GRNN光滑因子，建立最优的故障诊断模型。结果表明：采用PSO-GRNN模型可实现直升机旋翼不平衡的类型和程度的有效诊断，故障类型准确率高达94.29%，故障程度的诊断最大误差仅6.54%，满足工程需求。

振动与波；直升机旋翼；故障诊断；粒子群算法；广义回归神经网络

旋翼作为直升机的重要组成部分，其不仅能为直升机提供前进的动力，还能为各种姿态、机动变换提供动力来源。旋翼系统作为单通道的载荷传递系统，其工作环境复杂，承受了复杂的气弹载荷，尤其是在前飞过程中受到的不平衡周期交变载荷，容易使其关键部件产生振动和疲劳，容易产生故障而导致事故的发生。因此，对旋翼不平衡故障的诊断研究有着重大意义。

在对旋翼故障进行诊断识别的研究中，国内外很多学者采用了BP神经网络来实现诊断过程[1-4]。虽然这些建立的BP神经网络可以模拟直升机这一复杂的非线性系统，但BP神经网络需要很长的训练时间。而GRNN则具有收敛速度快的优点，并且相对于BP神经网络而言，其人为影响因素相对少很多。

下文选用GRNN网络来实现旋翼不平衡故障诊断，并引入粒子群算法来对GRNN模型参数进行优化，有效的解决了GRNN拓扑结构难以确定的问题，同时保留了GRNN非线性映射能力强、容错性和鲁棒性高的优点。通过有关文献数据的诊断验证了该方法的适用性。

1 PSO-GRNN模型建立

1.1 GRNN基本原理

GRNN由The Lockheed Palo Alto研究实验室的Donald Specht在1991年提出，其作为RBF神经网络的一种改进，建立在回归数理统计的基础上，能够根据样本数据逼近其中隐含的映射关系[5]。而且在样本数据稀少的情况下，也能达到较好的预报效果。其主要的优势体现在：GRNN网络具有良好的局部逼近性能，不会陷入局部极小值；不必进行循环的训练，计算速度快；需要调节的参数只有光滑因子d。

GRNN的理论基础是计算非独立输出变量Y相对于独立的输入变量X的非线性回归，得到概率最大的y。当给定矢量随机变量x的一个测量值为X时，随机变量Y的条件平均为

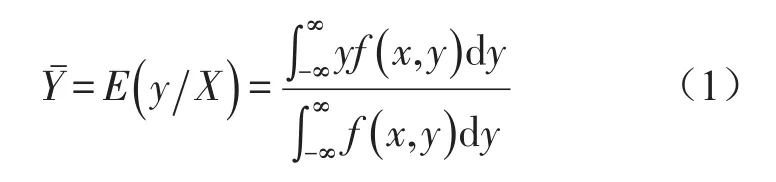
模型由4层网络构成，如图1所示，依次分为输入层、模式层、求和层和输出层。

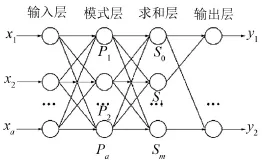
图1 GRNN拓扑结构图

其中，输入层接收样本的输入，其神经元数等于输入向量的维数，直接将输入变量传递给模式层；模式层即径向基层，其接收输入层传递的数据并输出与对应样本X之间的Euclid距离平方的指数平方的指数形式；求和层有两类神经元进行求和计算，分别对模式层神经元的分子单元和分母单元进行求和；输出层即将求和层的分子单元和分母单元的输出相除，得到最终的估计值。应用Parzen非参数估计的方法可知网络的输出为

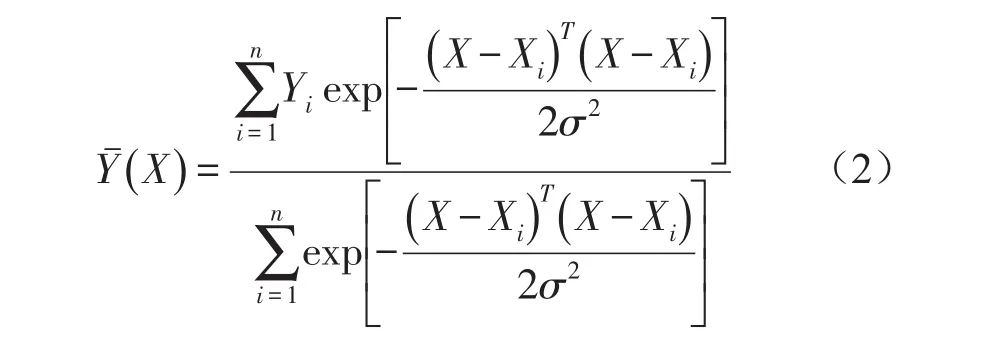
故在GRNN网络设计时，需要对光滑因子值进行寻优设计。光滑因子的选择起初是采用人工手动调节，而且大部分都采用经验值尝试，这就直接影响了GRNN网络的精度和效率。随着技术的进步，交叉验证成为了光滑因子选择的主流，但是由于每次变化过程中的步长为一定值，往往需要进行多次调节寻优范围和步长来实现寻优，这样也会严重制约光滑因子的选择。为减少光滑因子寻优时间，并提高GRNN网络精度和效率，下文采用粒子群算法结合交叉验证的思想来对光滑因子进行寻优求解。

1.2 基于粒子群算法的GRNN模型优化

粒子群算法（PSO）是一种基于群体智能理论的优化算法，由Eberhart博士和Kennedy博士提出，源于对鸟群觅食行为的研究[6]。在基本的PSO算法中，每个优化问题都是在搜索空间中的粒子，该粒子由位置、速度和适应度值三个指标来表述其特征。每次搜寻过程中，粒子通过跟踪两个“最优解”不断调整自己的位置和速度，进行更新。其中第一个就是粒子本身所找到的最优解，即个体最优解；其二为整个种群目前找到的最优解，即全局最优解。其粒子的更新过程如下所示

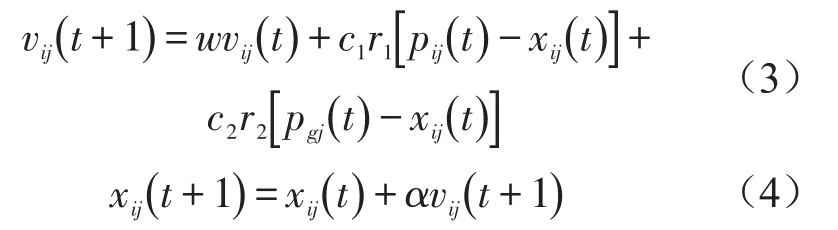
由上述介绍可知，需要对GRNN网络的光滑因子参数进行寻优，故优化问题转变为一个一维问题的粒子群寻优。其具体的算法流程如图2所示。

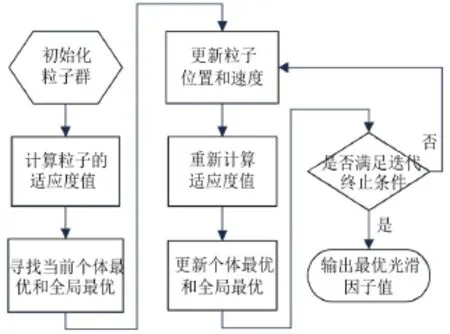
图2 PSO优化流程图

2 PSO-GRNN模型在直升机旋翼不平衡故障诊断中的应用

由于直升机旋翼的特殊性，在监测直升机旋翼状态的时候，很难直接在旋翼上安装传感器实现旋翼状态的监测，有关理论研究表明[7-9]，可以直接从直升机机体振动信号中提取特征向量来反映直升机旋翼状态，进而运用一定的模式识别方法对其进行状态诊断。

为实现旋翼不平衡故障的诊断，采用两类GRNN网络对故障类别和故障程度逐步进行识别。首先经过第一类GRNN网络作故障类型的诊断识别，建立故障类型诊断模型；在此基础上，对分类正确的故障信号，建立对应的第二类GRNN网络作故障程度的识别，建立故障程度诊断模型。最终实现旋翼不平衡的两步法诊断。

2.1 PSO-GRNN直升机旋翼不平衡故障类型诊断模型

直升机旋翼不平衡的故障类型很多，本文选取其中常见的三种故障（桨距不平衡、配重不平衡和调整片不平衡）进行模拟。文献[10]给出了105组单一不平衡故障样本，该样本来源于旋翼不平衡实验，通过测量旋翼试验台机体的振动信号，运用盲源分离的技术提取反映故障的特征向量，同时采用独立分量分析方法提取4维故障样本作为网络训练的输入样本，并将故障结果分为4类情况，即无故障、桨距不平衡、配重不平衡、调整片不平衡。分别以1/8、3/8、5/8、7/8数值量化代表其故障输出，输出数值按照等值区间量化判别。实验模型建立选取前35组样本进行交叉训练，运用PSO算法对光滑因子进行寻优，每次计算对应光滑因子下的均方误差，并以平均均方误差为适应度值对光滑因子进行迭代寻优，最终得到最优光滑因子值并建立PSO-GRNN故障类型诊断模型，并采用建立的模型对剩余样本进行故障类别诊断，样本如表1所示。

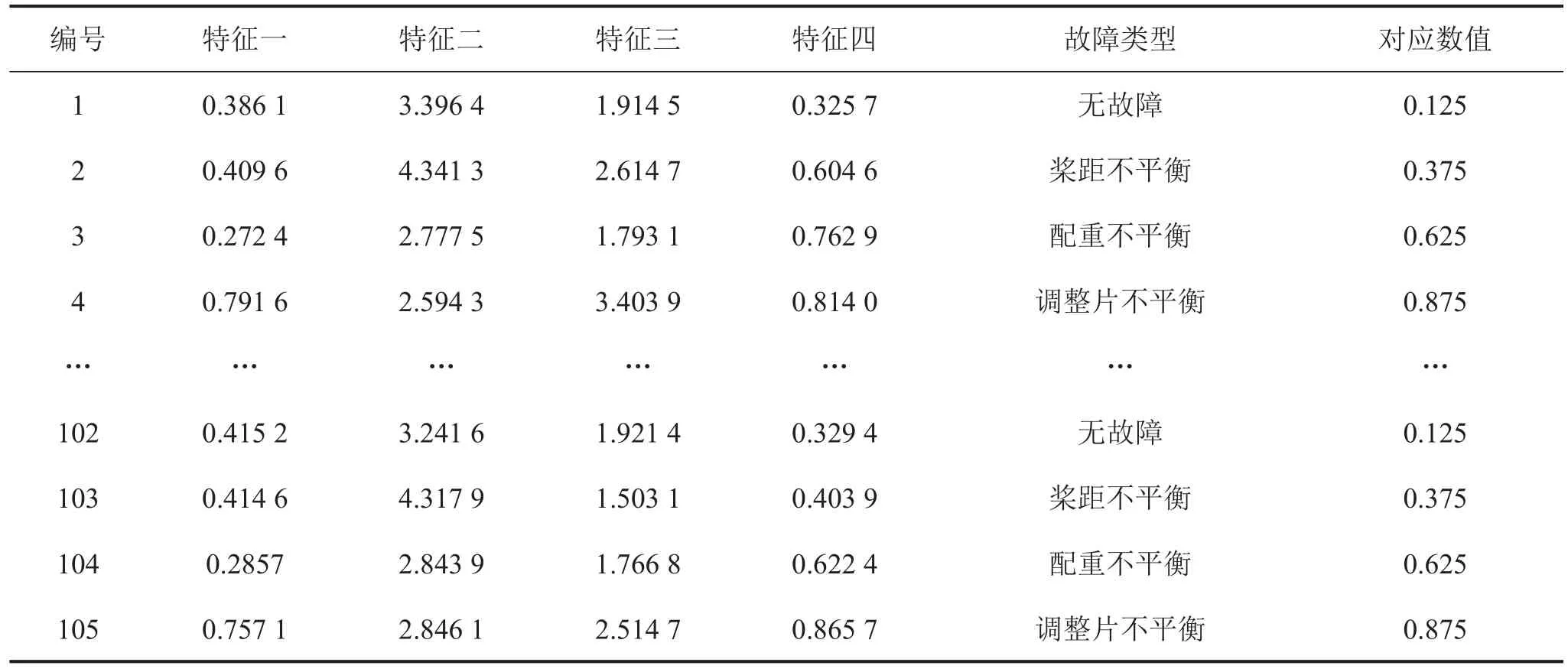
表1 PSO-GRNN故障类型学习和测试样本

根据文献[6]推荐的参数选择，设置PSO的参数为：种群粒子数为2，粒子的位置区间为[0.1，2]、速度区间为[-0.5，0.5]、惯性因子w取作0.9到0.4的线性递减值，加速因子c1、c2均取作2，迭代次数取作20，约束因子α为0.5。其具体迭代过程如图3所示。

由图3明显可见，经过16代寻优，PSO算法就能达到很好的寻优效果，其寻优结果为σ=0.265 4，此时最佳适应度函数值为0.008 3。

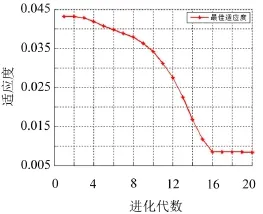
图3 光滑因子的迭代寻优过程

将得到的最优光滑因子σ=0.265 4建立GRNN故障类型诊断模型，并对剩余的70组样本进行诊断预测，分别计算各种故障类型的诊断准确率以及总体准确率，其故障类型的输出判别按照均匀分布原则在[0，1]间划分区间，即以0～0.25为无故障；0.25～0.50为桨距不平衡故障；0.50～0.75为配重不平衡故障；0.75～1.0为调整片不平衡故障。同时建立光滑因子为默认设置σ=1.0的模型并与文献[10]中的BP神经网络做预测对照分析，如表2所示。

表2结果表明，默认设置的光滑因子σ=1.0的GRNN模型能够对一部分故障进行有效的识别，特别是配重不平衡故障，能够达到识别率为100%，但对调整片不平衡类别诊断过程中，结果都误判为配重不平衡故障，不能对此故障进行有效识别，而且总体识别准确率不高，难以满足工程实际的要求。而经过PSO优化的PSO-GRNN故障类型诊断模型能有效的对上文所述的故障类别进行识别，并且可以总体上显著提高准确率；同时相对于文献[10]中所建立的BP神经网络，PSO-GRNN模型诊断的准确率也有一定程度的提高。

表2 PSO-GRNN与GRNN故障类别诊断模型准确率

2.2 PSO-GRNN直升机旋翼不平衡故障程度诊断模型

针对不同类型的故障，建立其各自相对应的故障程度模型。本文仅对配重不平衡故障作进一步的故障程度诊断，并建立对应的配重不平衡故障程度PSO-GRNN诊断模型。样本来源于不同配重质量下的机体振动信号[10]，经过数据处理提取出4维特征信号。其样本如表3所示：

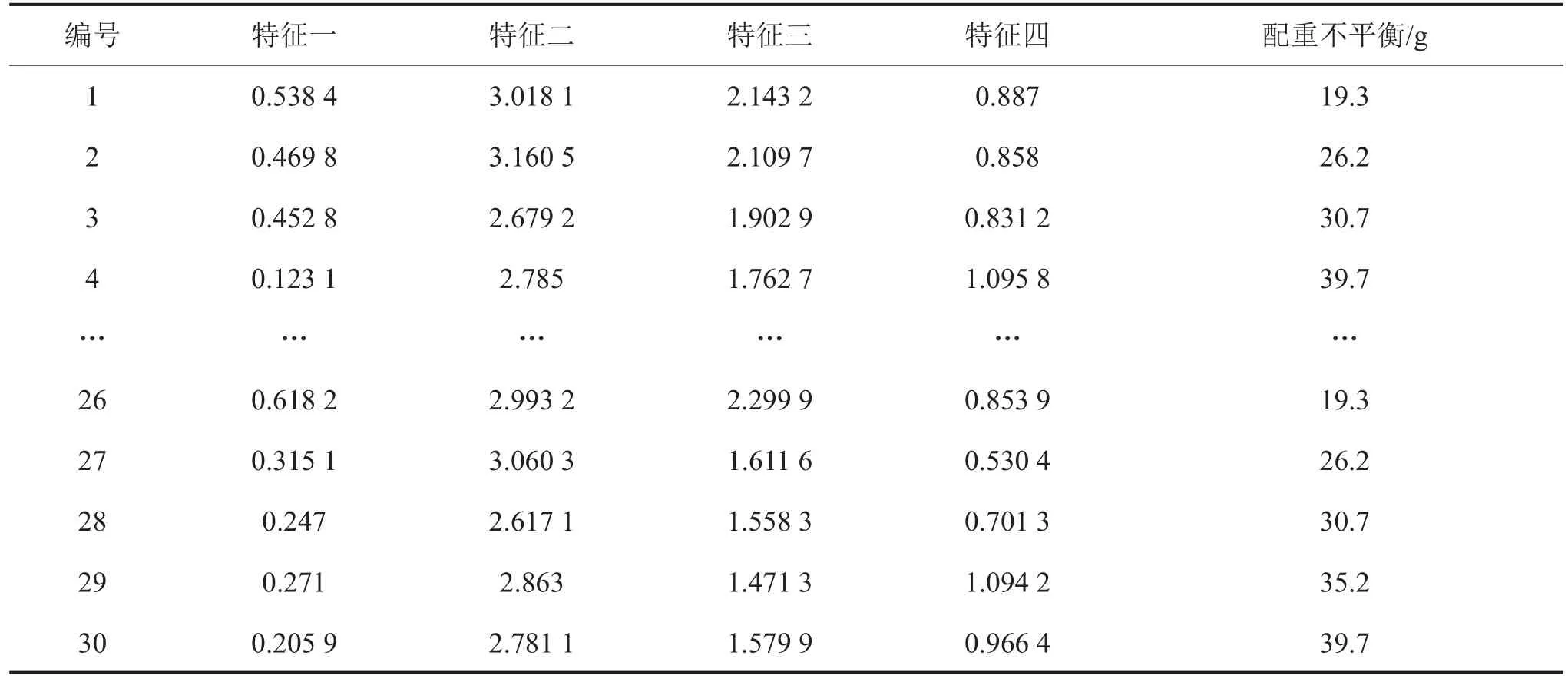
表3 PSO-GRNN配重不平衡故障程度学习和测试样本

同2.1中所述PSO参数设置对新建立的配重不平衡故障程度GRNN模型进行优化，由于考虑到样本数量少，为充分利用数据并防止数据出现过拟合现象，采用交叉验证方法得到的平均均方误差作为粒子群算法的适应度函数，搜寻最优的光滑因子。经PSO算法寻优得到最优光滑因子值为σ=0.549 9。并用前24组样本建立GRNN故障程度诊断模型，对26～30组数据进行预测分析，得到PSOGRNN模型的预测结果，与实际值对照如表4所示：

由表4中的结果可见，PSO-GRNN模型对故障程度的预测最大相对误差为6.54%，能达到较好的精度，能够满足工程需求。

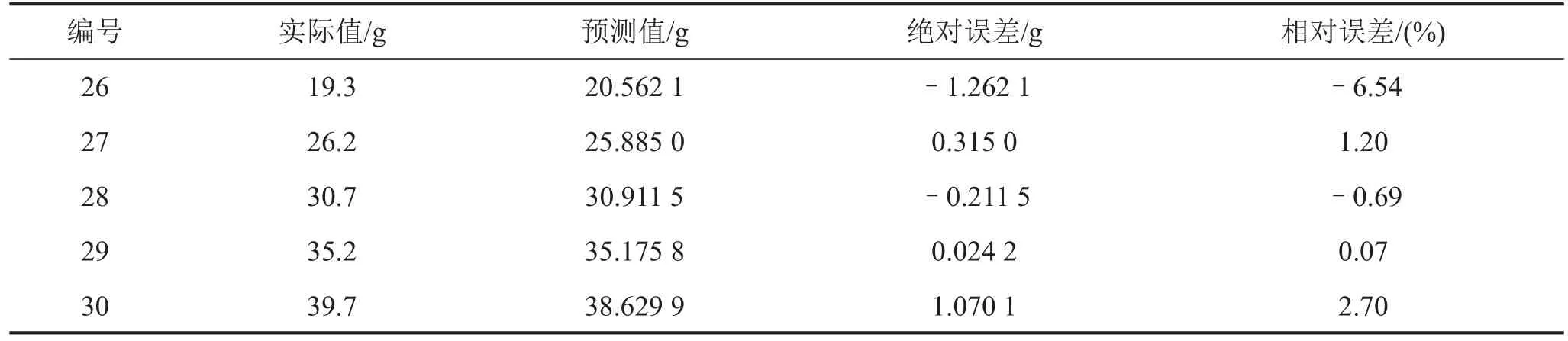
表4 PSO-GRNN预测结果与实测结果的比较

基于建立的PSO-GRNN模型的相同样本，建立对应的普通GRNN模型以及BP模型，并基于三种不同的模型分别对26～30组数据样本进行故障程度预测。

图4给出了后5组样本的PSO-GRNN模型预测结果和普通GRNN模型预测以及BP模型预测的对比图，图中明显可见PSO-GRNN模型预测的优越性，其相对误差最小。

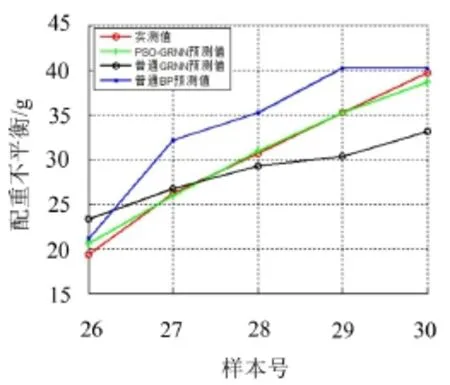
图4 预测结果对比图

3 结语

（1）针对广义回归神经网络光滑因子难以选取的现状，采用粒子群算法对广义神经网络的光滑因子进行优化，有效的减少了人为因素对预测结果的影响；

（2）提出并建立了直升机旋翼不平衡的两步法诊断模型，采用文献数据对模型进行训练和测试，结果表明，PSO-GRNN两步法模型可有效的诊断故障类型和故障程度，而且故障类型准确率高达94.29%，故障程度的诊断最大误差仅6.54%，满足工程实际的应用；

（3）文献数据诊断对比分析结果表明，PSOGRNN诊断模型效果明显优于BP模型和普通的GRNN模型。

[1]Pawar PM,Ganguli R.Helicopter rotor health monitoring-a review[J].Journal of Aerospace Engineering，2007,221 (G):631-647.

[2]Ganguli R,Chopra I.Helicopter rotor system fault detection usingphysics-basedmodelandneuralnetworks[J].Journal ofAircraft,1998,36(6):1078-1086.

[3]高亚东，张曾锠，余建航.用机体振动诊断直升机旋翼失衡故障方法研究[J].振动工程学报，2002，15(4)：395-398.

[4]高亚东，张曾锠，余建航.用机体振动诊断直升机旋翼复合不平衡故障研究[J].航空学报，2004，25(1)：26-30.

[5]史峰，王辉，郁磊，等.Matlab神经网络30个案例分析[M].北京：北京航空航天大学出版社，2009：73-80.

[6]刘波.粒子群优化算法及其工程应用[M].北京：电子工业出版社，2010：27-47.

[7]高亚东，张曾锠.用机体振动信号诊断旋翼不平衡故障的理论基础[J].振动、测试与诊断，2003，23(4)：279-282.

[8]高亚东，张曾锠.直升机旋翼不平衡故障诊断试验研究[J].振动、测试与诊断，2009，29(2)：214-217.

[9]邓升平.旋翼不平衡故障试验及诊断方法研究[D].南京：南京航空航天大学，2010.

[10]姚飞虎.基于盲源分离和人工免疫的旋翼故障诊断[D].南京：南京航空航天大学，2011.

[11]杨茂，李小龙.基于仿真数据的旋翼系统故障识别[J].浙江大学学报(工学版)，2013，47(12)：2188-2194.

[12]刘红梅，吕琛，欧阳平超.粒子群优化在直升机旋翼动平衡调整中的应用[J].北京航空航天大学学报，2011，37(3)：283-288.

Fault Diagnosis of Helicopter Rotor’s Unbalance Based on PSO-GRNNAlgorithms

XIE Xi-hua1,2,XU Lei1,TAN Yao1,MA Yun-rong1
(1.State Key Laboratory of High Performance Complicated Manufacturing,Central South University, Changsha 410083,China; 2.The National Enterprise R&D Center,Sunward Intelligent Equipment Co.Ltd., Changsha 410100,China; 3.Collaborative Innovatim Center for Soutiern Grain and Oil Grop.,Changsha 410100,China)

In order to diagnose the helicopter rotor’s unbalance fault accurately,a method based on particle swarm optimization(PSO)algorithm and generalized regression neural network(PSO-GRNN)was proposed.The average mean square error obtained from cross validation was used as the fitness function of the particle swarm.Then,the optimal GRNN smooth factor was attained by using the PSO algorithm,and an optimal model for fault diagnosis was achieved.It can be concluded that based on the PSO-GRNN model,the type and the extent of the helicopter rotor’s unbalance can be diagnosed effectively,the accuracy rate of fault type is up to 94.29%and the maximum error of fault degree is only 6.54%,which satisfies the requirement of engineering projects perfectly.

vibration and wave;helicopter rotor;fault diagnosis;particle swarm optimization;generalized regression neural network

TP206.3;V275.1

A

10.3969/j.issn.1006-1335.2015.02.039

1006-1355(2015)02-0175-05

2014－09－15

湖南省教育厅高新科技成果产业化培育项目(12CY001)；湖南省重大科技成果转化项目(2012CK1003)

谢习华(1969－)，男，硕士生导师。E-mail:xxh_zh@csu.edu.cn

徐雷(1991－)，男，湖北黄冈人，硕士生，主要研究方向：直升机旋翼故障诊断,直升机系统辨识。