能力评估系数的发展

姜月娇

(哈尔滨师范大学)

0 引言

认知领域中，许多理论和方法的建立都是基于四个主要的人类信息加工特性:随工作量变化的效率(efficiency)，包括无限能力、有限能力;精神构架(mental architecture)，包括并行处理系统(parallel)、串行处理系统(serial)或其他更复杂的系统;停止准则(stopping rule)，包括OR停止准则、AND停止准则等;通道(channel)、目标(item)等的独立性．

并行处理是指试验中所有目标同时出现并可以同时处理的情况;串行处理是指实验中的目标是分先后顺序出现的，只有前面的目标检测(detect)完毕，后面的目标才可以出现的情况．OR停止准则是指在目标有两个或两个以上的试验中，被试只要识别出目标中的任何一个都可以做出反应;AND停止准则是指在目标有两个或两个以上的试验中，被试必须识别出所有的目标才可以做出反应．

认知心理学的很多研究中，像视觉搜索、视觉感知、听觉感知等方面，工作量增加时对处理发生的改变进行测量是很重要的．能力系数就是量化这种改变的一种基于反应时间的测量．早期的工作量能力评估是通过比较单目标条件下与多余目标(redundant target)条件下做出肯定回答的反应时间来实现的，人们会把平均反应时间作为衡量工作量能力的首选统计量．Townsend和Ashby1978年在处理过程中提出了使用冒险函数测量能力，为能力研究提供了一个高度清晰的途径．1982年，Miller在OR范例中提出了针对通道的反应时间的上界［10］;同样地，Grice和他的学生在1984年提出了OR范例的下界［5］．界理论的提出为能力的分类提供了一个方法．

在上述用反应时间作为度量工作量能力的指标时，增加目标对处理效率产生了哪种影响是不清楚的，是改善了效率，还是降低了效率，亦或是没有影响呢?例如，在一个系统中，假设目标是并行的、独立的分开处理的，当目标数量增加时，平均反应时间减少．表面上看，似乎能力是增加的，但是实际上却是无限能力［4］．

1 仅基于反应时间的能力评估函数

1．1 OR停止准则下的能力评估函数

为了避免上述分歧，1995年，Townsend和Nozawa首次提出了仅基于反应时间的能力评估函数 C0(t)［14］．

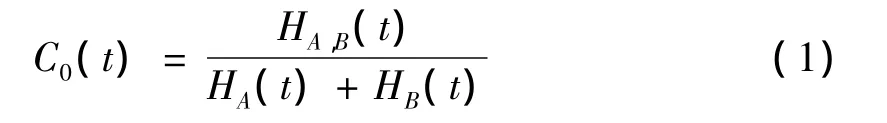
该理论包括了人类信息加工的四个特性:效率随工作量的变化情况、精神构架、OR停止准则和系统的独立性．通过比较C0(t)与1的大小关系，实现了将待测系统的能力分类的目的．当C0(t)大于1时，待测系统为超大能力，是比标准并行处理更快的处理;当C0(t)小于1时，待测系统为有限能力，是比标准并行处理更慢的处理;当C0(t)等于1时，待测系统就是标准并行处理．C0(t)理论还使用了Miller不等式和Grice不等式来对系统能力进行分类．

1．2 AND停止准则下的能力评估函数

1994年，Colonius和 Vorberg提出了AND准则下的上下界［3］，它类似于OR准则中的Miller界和Grice界，并称它为Colonius-Vorberg不等式．

2004年，Townsend和Wenger又提出了AND停止准则的Ca(t)函数形式［15］．

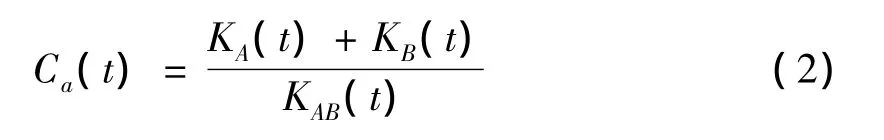
与OR停止准则使用冒险函数h(t)不同的是，在AND中，使用了类似于冒险函数的k(t)函数．最后得到了类似于C0(t)的形式．通过将Ca(t)与1进行比较，也达到了分类的目的．当Ca(t)大于1时，待测系统有超大能力，比标准并行系统更快;当Ca(t)小于1时，待测系统有有限能力，比标准并行系统更慢;当Ca(t)等于1时，待测系统为无限能力，Ca(t)与标准并行系统相同．理论还使用Colonius-Vorberg不等式来对系统进行分类．

通过上面的总结可以看到，无论是使用界理论还是工作量能力理论，都可以实现对系统能力分类的目的．但是使用不同的理论进行比较时，所使用的统计量是不同的．在界理论中使用的是反应时间的分布函数，而在工作量能力理论中，使用的却是C(t)函数．所以在进行比较时需要一些转换．

2011年，James T．Townsend和 Ami Eidels两个人通过使用概率论和数学中的一些简单计算，提出了一个把不同空间中用于提供效率说明的各种统计量统一起来的一个方法，即把各个界变换成了C(t)函数的上下界，从而可以把上下界和C(t)函数画在同一张图上，并且可以直接进行互相比较［7］．但是在OR准则下，用转化后的界去对能力进行分类时评价准则发生了一些改变:在Miller空间，只要分布函数超过这个界就可以说该系统能力是超大的．当把Miller界转换成能力空间中的界时，通常它会大于1，暗示着，这个界会是超大能力的保守估计．也就是说，一个系统也许有超大能力，然而C(t)值也许会在界下面，并没有超过它．

对于race model界的统计检验已经有很多了［6，16］，但是对于能力系数的统计检验却很少．仅有的可用于有两个信息通道的能力系数的定量检验［2］在文献中也有提出，但这却要基于“每个通道要用LBA模拟”的假设下．2011年，Houpt和Townsend两人提出了一个非参数的可用于任意多个信息通道的能力系数的综合性的统计检验［9］．两人在文中证明了OR和AND两个停止准则下的工作量能力系数的组成成分(累积冒险函数和累积反冒险函数)的统计性质，并且在文献的附录中给出了每个性质的详细证明过程．同时提出了一个用于比较待测系统和基线测量(标准并行系统)或两个能力系数互相比较的显著性检验．文中在构造统计量时，作者没有使用经验累积冒险函数去估计冒险函数，而是使用了NA估计量［1］，从而简化了计算．

由于race model不等式及OR、AND下的能力系数对区别系统的动态性质方面有它们特殊的优点，故在认知心理学的很多方面都在应用．如记忆搜索［12］、危险侦察［11］等．

2 选择反应时的LBA模型及其重要应用

2．1 LBA 模型

2008 年，Scott D． Brown 和 Andrew Heathcote提出了选择反应时的LBA(linear ballistic accumulation)模型［2］．该模型比其他选择反应时模型更简单．它的本质是结束一个反应所花费的时间的概率密度函数．它的思想是:模型中每个通道的每个回答(yes和no)都用一个累加器来代表，每个累加器中的迹象(activity)以线性和确定性的方式增长，当某一个累加器到达反应阈值时，反应停止．这时也就得到了反应时间和反应结果．通过模型的计算，还可以得到选择该结果所花费时间的概率密度函数和累计分布函数．由于该模型迹象起始点大小的可变性和累计速度(drift rate)的可变性二者之间的相互作用，故可以实现准确率和反应时间之间的权衡．

2．2 LBA模型的一个重要应用

2010年，Ami Eidels等人应用LBA模型将能力评估函数推广到了参数模型的水平．这就使得在判断系统能力时，可以更客观的得到结论．作者运用简单的概率论知识先将LBA模型推广到多余目标任务模型(redundant-target task model)中，得到在任务中做出肯定反应和否定反应的相应概率．运用最优化算法可以得到最合适的参数．然后通过比较单目标条件和双目标条件下的累计速度(drift rate)来判断能力的类别．若累计速度没有因为目标的增加而改变，则能力是无限能力;若累计速度随着目标的增加而减少或增加，则能力被认为是有限能力或超大能力［4］．

3 基于准确率与反应时间的能力评估函数

上面的理论都只是基于反应时间，并没有将准确率融合进来．那么要获得正确反应和错误反应对系统的贡献，通过上面的理论是无法实现的．因此把准确率融入进来就显得相当重要了．

2012年，Townsend和Altieri首次将准确率和反应时间结合起来，发展了一套比较完整的理论［8］．该理论包含了上面提到的人类信息加工的四个特性，并研究了AND和OR两种停止准则下的能力评估函数．由于考虑了准确率，实验结果就被分为了四类进行研究．包括:正确快速(CF)、正确慢速(CS)、错误快速(IF)和错误慢速(IS)四种情况．通过将A(t)与1进行比较，来实现对系统的分类．该理论也发展了一套不等式，也就是A(t)函数的上下界，从而可以由另一个角度来对模型能力进行分类．因为考虑了四种情况，那么哪一种情况是结果最佳的呢?也就是说我们怎么在准确率和反应时间二者之间进行取舍呢?理论中也通过将A(t)函数分解来对准确率和反应时间进行了一个权衡(trade-off)．最后在OR准则下得出结论:慢速是最好的情况，在慢速要求下，准确率提高，系统能力也相应的提高．但是在AND情况下，无论快慢，错误率都很高，正确反应与错误反应的判断标准都被放松．但是，慢速也给系统能力带来了一定的改善．通过分解，也对系统能力改变的原因进行了分析．在OR准则下，由于准确率几乎没有发生改变，故能力的改变主要是由于反应的快慢引起的．在AND准则下，准确率大幅退化，能力的改变有反应时间的原因，准确率应该也有一定的影响．

4 结束语

仅基于反应时间的能力评估函数实现了从非参数模型向参数模型的转变，但是正确反应和错误反应的贡献却无法从模型中得到．那么有了基于准确率和反应时间的能力评估函数以后，就可以获得正确反应和错误反应对系统的贡献了．但是，这个理论是非参数的，不能从模型中获得结果的改变是由那个变量引起的．如果能发展一套基于准确率和反应时间的参数模型的话，那么将会是能力评估领域的一个重大进步．

［1］ Aalen O O，Borgan Ø，Gjessing H K．Survival and event history analysis:a process point of view．New York:Springer，2008．

［2］ Brown S D，Heathcote A J．The simplest complete model of choice reaction time:Linear ballistic accumulation．Cognitive Psychology，2008，57:153-178．

［3］ Colonius H，Vorberg D．Distribution inequalities for parallel models with unlimited capacity．Journal of Mathematical Psychology，1994，38:35-58．

［4］ Eidels A，Donkin C，Brown S D，et al．Converging measures of workload capacity．Psychonomic Bulletin ＆ Review，2010，17:763-771．

［5］ Grice G R，Canham L，Gwynne J W．Absence of a redundant-signals effect in a reaction time task with divided attention．Perception ＆ Psychophysics，1984，36:565-570．

［6］ Gondan M，Riehl V，Blurton S P．Showing that the race model inequality is not violated．Behavior Research Methods，2012，44:248-255．

［7］ James T，Townsend，Ami Eidels．Workload capacity spaces:A unified methodology for response time measures of efficiency as workload is varied．Psychon Bull Rev ，2011，18:659-681．

［8］ James T．Townsend，Nicholas Altieri．An Accuracy-Response Time Capacity Assessment Function That Measures Performance Against Standard Parallel Predictions．Psycholog-ical Review，2012，119(3):500-516．

［9］ Joseph W．Houpt，James T．Townsend．Statistical measures for workload capacity analysis．Journal of Mathematical Psychology，2012，56:341-355．

［10］ Miller J．Divided attention:Evidence for coactivation with redundant signals．Cognitive Psychology，1982，14:247-279．

［11］ Richards H J，Hadwin J A，Benson V，et al．The influence of anxiety on processing capacity for threat detection．Psychonomic Bulletin and Review，2011，18:883-889．

［12］ Rickard T C，Bajic D．Memory retrieval given two independent cues:cue selection or parallel access?Cognitive Psychology，2004，48:243-294．

［13］ Townsend J T，Ashby F G．Methods of modeling capacity in simple processing systems．Cognitive theory，1978(3):200-239．

［14］ Townsend J T，Nozawa G．Spatio-temporal properties of elementary perception:An investigation of parallel，serial，and coactive theories．Journal of Mathematical Psychology，1995，39:321-359．

［15］ Townsend J T，Wenger M J．A theory of interactive parallel processing:New capacity measures and predictions for a response time inequality series．Psychological Review，2004，111:1003-1035．

［16］ Ulrich R，Miller J，Schröter H．Testing the race model inequality:an algorithm and computer programs．Behavior Research Methods，2007，39:291-302．