维基百科人物关系知识网络的复杂性分析

(杭州电子科技大学认知与智能计算研究所，浙江 杭州310018)

0 引 言

采用复杂网络理论与方法来分析维基百科的知识网络在国内外已有一些研究。文献[1]将英文版维基百科的文章网络作为一个语义知识网络进行研究。文献[2]分析了中文版维基百科2004-2012年的类别网络及其演化规律。文献[3-4]分别研究了中文版维基百科的文章网络、类别网络和用户网络，发现其小世界等复杂网络特性。文献[5]将维基百科类别网络与WordNet、同义词词林等3个概念网络分别看作自组织知识网络与他组织知识网络的代表，发现它们在微观结构上具有相似性。众所周知，维基百科词条涉及的范围极其广泛，而现有研究工作都不是面向特定类别词条的。研究包含所有词条的文章网络，对于发现维基百科知识组织的宏观结构和演化规律具有一定意义，但是对于挖掘粒度更小的领域知识就显得力不从心。本文研究维基百科文章网络的一个子集——人物关系知识网络。选择维基百科中的人物词条，并根据人物词条之间的超链接关系构建知识网络。然后采用复杂网络分析方法对该网络进行研究，发现了一些有意义的现象和规律，对于推动基于维基百科的专门领域知识网络的分析与挖掘研究具有一定意义。

1 数据来源及网络构建

从网址http://dumps.wikimedia.org/zhwiki/latest/下载最新中文版维基百科数据库，和本文相关的主要是pages-articles(词条集合)、pagelinks(词条之间的链接)、category(类别)几部分。对以上数据进行整理和抽取。从pages-articles 中选择类别属于“人物”及“人物”下面子分类的词条，构成本文知识网络的节点集合V。然后从pagelinks 中抽取头节点和尾节点均属于V的链接，构成知识网络的有向边集合E。由V和E 构成的有向图(V，E)即为本文原始人物关系知识网络，记为W_NET。

将W_NET 转换成Pajek[6]可以识别的格式，计算其基本参数，包括节点数(N)、有向边数(A)、网络直径(D)、平均度(＜k ＞)、平均最短路径长度(L)、聚类系数(C)和网络密度(d)。通过计算，发现W_NET 中存在一个包含28 881个节点(占总节点数的91.792 3%)的最大弱连通子图(记为C_NET)。W_NET和C_NET 基本参数如表1所示。没有包含在C_NET中的节点，基本上都是冷僻、孤立的词条，不具有代表意义。若不加说明，本文后面的分析只针对C_NET。

表1 网络基本参数

2 网络总体特性

2.1 基本参数分析

C_NET 共包含288 81个节点，114 319条有向边。网络直径为43，平均最短路径长度为7.976 54，与社会学“六度分离”理论[7]中的数字6 相比略大。原因应该是C_NET 包含古今中外不同时期的人物，而“六度分离”理论的结论来自同一时代的人群。

网络密度描述一个网络中节点之间关联的紧密程度，是网络凝聚力总体水平的体现。设网络有n个节点，m为网络实际存在的边的数量，则有向网络的密度可由下式计算:

聚类系数是网络的局部特征，反映两个相邻节点之间朋友圈子的重合度。一个网络的聚类系数C 定义为网络中所有节点的聚类系数的平均值。设网络中节点i的度为ki，i的ki个邻居节点之间实际存在的边数为Ei，则节点i的聚类系数Ci可由下式计算:

经过计算，C_NET的网络密度为0.000 147 1，聚类系数为0.069 709 7。与一般的社会网络比较均偏小[8]，这与C_NET是有向图以及它的节点涵盖范围广有关。

2.2 小世界特性

如果一个网络的平均最短路径长度(L)与由相同节点数和相同边数构建的相同规模随机网络的平均最短路径长度近似相等，而网络的聚类系数(C)接近相同规模的规则网络，远大于相同规模随机网络的聚类系数，那么可以认为这个网络是小世界的。

如表1所示，C_NET的平均最短路径长度L=7.976 54，聚类系数C=0.069 709 7。构建与C_NET节点数和边数相同的随机网络Cr_NET，并对相关参数计算得Lr=7.376 661、Cr=0.000 156 9。由于L ≈Lr，而C ＞＞Cr，可知C_NET 具有明显的小世界特性。

2.3 无标度特性

通常将度分布符合幂律分布的复杂网络称为无标度网络。网络的度分布p(k)定义为网络中随机选取的一个节点其度恰好为k的概率。在双对数坐标下，通过计算累积度分布曲线来表示度分布，如果度分布是幂律指数为γ的幂律分布，那么累积度分布就是幂律指数为γ-1的幂律分布。对于C_NET，分别计算其入度、出度累积度分布，如图1、图2所示。

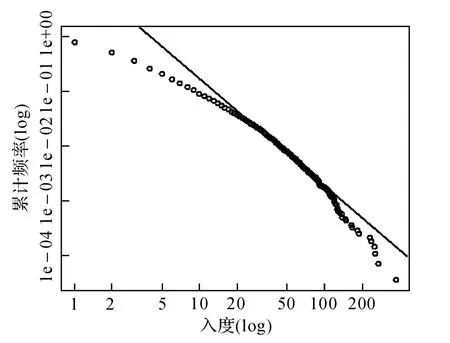
图1 入度累积度分布

图2 出度累积度分布

通过幂律拟合，入度分布符合幂律指数为2.96的幂律分布，出度分布符合幂律指数为2.57的幂律分布，可见C_NET是一个具有无标度特性的复杂网络。

3 重要节点分析

在维基百科人物关系网络中，哪些人物处于中心位置，哪些人物比较重要，是本文比较关心的问题。节点重要性可以从点度中心度、介数中心度、接近中心度几方面来衡量。

点度中心度单纯从节点的度数来考察节点重要性。在有向网络中分为入度和出度，入度表示指向该节点的连接数，出度表示由该节点指出的连接数。直观来看度数越大意味着这个节点在某种意义上越重要。设网络有n个节点，k为节点度，则点度中心度可以定义为:

C_NET 中入度最大的10个节点如表2所示，其中国家领导人及历史名人的入度相对来说比较大，说明在维基百科中他们作为关系人物出现在他人介绍页面上的次数较多。

表2 入度最大的10个节点

出度最大的10个节点如表3所示，大多是娱乐圈中的人物，他们的出度之所以相对其他人来说比较大，是因为作为娱乐圈人物，他们的社会关系丰富，一起合作的人物非常多。

表3 出度最大的10个节点

节点的介数是一个描述网络动态的全局中心度指标，其分布特征对于发现和保护关键资源具有重要意义。设网络有n个节点，gij(x)为节点j和k的最短路径中经过节点x的条数，则节点x的介数中心度可以定义为:

本文C_NET 网络中，人物节点介数的分布特征反映的是相应人物在社会关系中的地位。C_NET 中介数最大的10个节点如表4所示。

表4 介数最大的10个节点

接近中心度是一个刻画节点通过网络到达其它节点难易程度的指标。设网络有n个节点，dxy为节点x 到节点y的最短路径长度，则节点x的接近中心度可以定义为:

在有向网络中，接近中心度根据节点出入不同方向又可分为内接近中心度和外接近中心度，可以分别测量。C_NET的内、外接近中心度最大的10个节点分别如表5、表6所示。

表5 内接近中心度最大的10个节点

表6 外接近中心度最大的10个节点

以上3个指标从不同角度对节点重要性进行衡量，各有其基本原理和侧重。通过对C_NET 中心性的分析，发现其入度中心度(见表2)、介数中心度(见表4)、内接近中心度(见表5)的TOP 10 节点重合度很高，而出度中心度(见表3)、外接近中心度(见表6)的TOP 10 节点也有诸多类似。普遍地，当代的词条基本都集中在娱乐圈，古代的词条基本都是著名政治人物。由于维基百科是一个由网络用户自由编撰的、内容开放的网络百科全书，其词条的编撰和内容的丰富程度与普通百姓的兴趣点密切相关，因此C_NET中的重要节点均为著名娱乐圈人士和政治风云人物就不奇怪了。

4 社团分析

大量研究表明，社会网络普遍存在模块化结构[9]。C_NET 由人物节点构成，对其进行社团分析具有重要意义。针对网络规模及算法的时间复杂度，发现基于随机游走的walktrap算法[10]是最合适的选择。walktrap算法试图利用随机游走的方式发现网络中连接最紧密的子图，其核心思想为最短的随机游走趋向于停留在相同的社区。利用R 语言的igraph 包提供的随机游走算法对C_NET 进行社团检测，共得到225 1个社团，模块度值为0.688 246 2。对划分的社团规模进行分析，发现它与实际复杂网络的社团规模分布类似，符合幂律分布。在225 1个社团中，人数在10个以上(包含10个)的社团有249个，分别对这249个社团进行基本参数计算，特别关注反映社团紧密程度的聚类系数和网络密度，发现有13个社团的聚类系数和密度均位于前20位，说明它们的内聚性比较强，具有代表意义。其基本情况如表7所示。

表7 社团基本情况

分析这13个典型社团中的成员情况，发现他们基本都是通过家族、职业、事件而关联在一起的，即他们或者是同一个家族中的成员，或者从事同一种职业，或者共同经历了某一历史事件，再或者是某一个团体。就以550 号社团为例，他们绝大部分是来自不同国家花式台球职业选手，基于共同职业聚在一起，其他社团分析结果具有类似情况。通过以上分析，发现采用随机游走算法从C_NET 中挖掘出的社团是合理且有意义的。

5 结束语

专门领域的知识网络研究是当前智能信息处理研究领域的重要课题，维基百科作为目前最大的在线知识库，正成为知识网络研究的热点。本文研究的是维基百科中的人物关系知识网络，后续可利用本文的研究方法对维基百科中的其他分支领域进行研究，预期将会发现更多的领域知识和规律，为各类网络应用提供支撑。

[1]Masucci A P，Kalampokis A，Eguíluz V M，et al.Wikipedia Information Flow Analysis Reveals the ScaleFree Architecture of the Semantic Space[J].PLoS ONE，2011，6(2):1-7.

[2]Wang Q，Wang X，Chen Z，et al.The Category Structure In Wikipedia∶To Analyze And Know How It Grows[M]//Chinese Lexical Semantics.Berlin:Springer Berlin Heidelberg，2013:538-545.

[3]杨祎.Wiki 知识网络的网络特性与演化模型研究[D].杭州:浙江理工大学，2013:61-76.

[4]赵飞，周涛，张良，等.维基百科研究综述[J].电子科技大学学报，2010，39(3):321-334.

[5]宋倩倩，关婉湫，张淑君，等.组织知识系统与他组织知识系统的网络结构比较分析[J].情报理论与实践，2010，(3):115-119.

[6]孟微，庞景安.Pajek 在情报学合著网络可视化研究中的应用[J].情报理论与实践，2008，31(4):573-575.

[7]Milgram S.The small world problem[J].Psychology Today，1967，2(1):61-67.

[8]苑卫国，刘云，程军军，等.微博双向“关注”网络节点中心性及传播影响力的分析[J].物理学报，2013，62(3):038901.

[9]Ahn Y Y，Han S，Kwak H，et al.Analysis of topological characteristics of huge online social networking services[C]//Proceedings of the 16th international conference on World Wide Web.Alberta:ACM，2007:835-844.

[10]Li J.Evaluating community structure in the large network with random walks[C]//Science and Information Conference(SAI)，London:IEEE，2013:315-319.