基于类Lorenz的微弱信号检测及其电路实现
2015-12-02
(杭州电子科技大学机械工程学院,浙江 杭州310018)
0 引 言
1963年,Lorenz 对天气预报相关数据进行处理时发现了混沌现象[1]。近年来,混沌理论渗透到各个领域内,利用混沌理论解决工程实际问题越来越多地受到人们关注。其中,利用混沌理论实现对噪声背景中的微弱信号的检测就是一个重要应用[2-5]。时至今日,已有很多混沌控制方法被学者和研究人员提出,如OGY(Ott-Grebogi-Yorke)方法[6-7]、自适应控制法[8]、参数周期微扰法[9-10]等,这些方法在实际应用中取得了很好的效果,但是其参数阈值的计算过程比较复杂。本文提出了一种改进的参数周期微扰法,把系统状态控制在对应的周期轨道内,不仅控制结构简单,而且对混沌参数阈值计算过程复杂、控制范围小的问题作了一定地改善,并利用电路从噪声背景中检测出微弱的中低频周期信号。
1 类Lorenz系统模型
本文提出一种具有类似Lorenz 混沌系统特性的新三维系统,称之为类Lorenz系统。系统的微分方程如下:

式中,a、b、c均为系统参数,xz、xy为非线性项。取:

在类Lorenz系统a、b、c 参数中,改变其中任一参数都会引起混沌状态的改变。文中以b为例,求出了类Lorenz 混沌系统随参数b 变化的Lyapunov 指数谱和分岔图别如图1和图2所示。通过分析Lyapunov[11]和分岔图[12]可以定量地判断系统所处的状态。
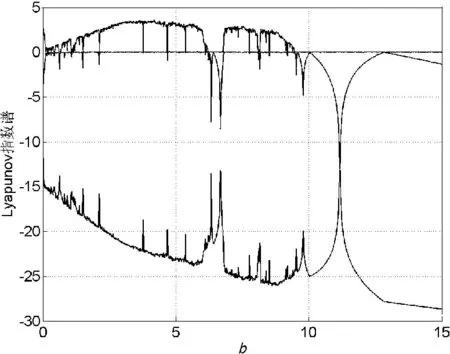
图1 关于参数b的Lyapunov 指数谱
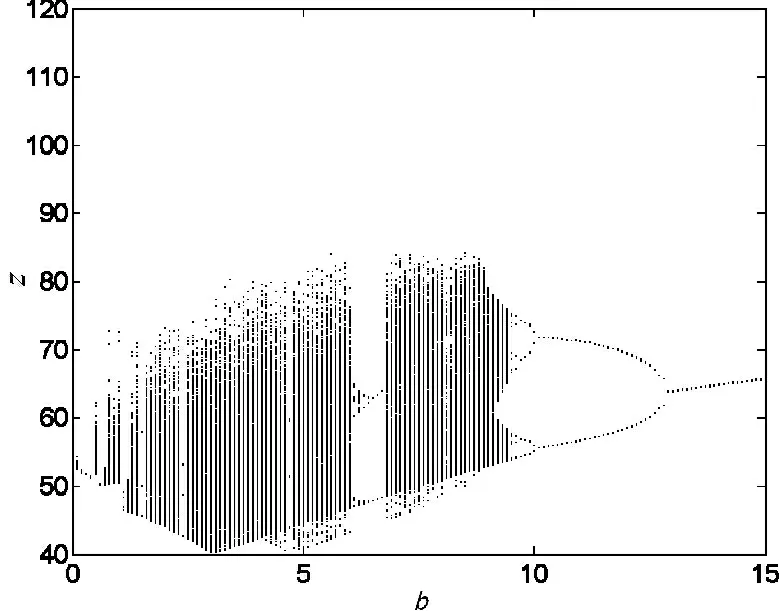
图2 类Lorenz系统z 关于b的分岔图
图1揭示了系统的Lyapunov 在参数a=35,c=20 下随参数b 变化的特性。当参数a=35,b=6,c=20时系统最大Lyapunov 指数是L1=1.608 7,L2=0,L3=-25.599 6。存在正的Lyapunov 指数,可见在上述参数条件下系统是一个随参数b 变化的混沌系统。而且由图2可以确定混沌系统发生状态转变的临界值。
2 双参数微扰法的混沌控制
考虑可调多参数时间连续n维系统:

式中,x=(x1,x2...,xn)为n维系统变量,b =(b1,b2...,bs)为系统的s个连续可调参数。将其中一参数bλ(bλ>0,1≤λ≤s)选定作为周期微扰的对象。令bλ' =bλ(1+h(t)+m),其中h(t)=rcos(ωt)为周期性控制信号,r为幅值,r∈R 且r≠0,ω为频率,m为常数,当r≠0,m≠0时,假设系统(3)处于一周期态的参数范围为[ k1,k2],即:

可得关系式如下:

根据式(4)可以计算出系统式(2)处于此周期态是r和m的范围,在这个范围内选择适当的r和m,就可以把系统稳定在这个周期轨道上。
代入类Lorenz系统式(1),其受控方程如下:

采用四阶Runge-Kutta 方法,取系统初始值x0=1.2,y0=0.6,z0=2.5,参数a =35,b =6,c =20,周期性控制信号h(t)的频率f=1 Hz,相位φ=0,适当地调整m,r值,系统状态可被控制在不同的周期轨道内,因此,同时改变m,r值来控制系统状态变化的方法称为双参数微扰法。系统在各个周期状态时的x-z 平面相图如图3所示。

图3 各个周期状态时的x-z 平面相图
3 基于类Lorenz系统的微弱信号检测电路
3.1 微弱正弦信号检测电路原理
根据式(1)所示系统结构,系统主要由求和、放大、积分等部分组成,其原理如图4所示。图4中,系统结构的各个部分可以通过运算放大器、乘法器、电阻、电容等元件组成。由此得到混沌检测电路,如图5所示。
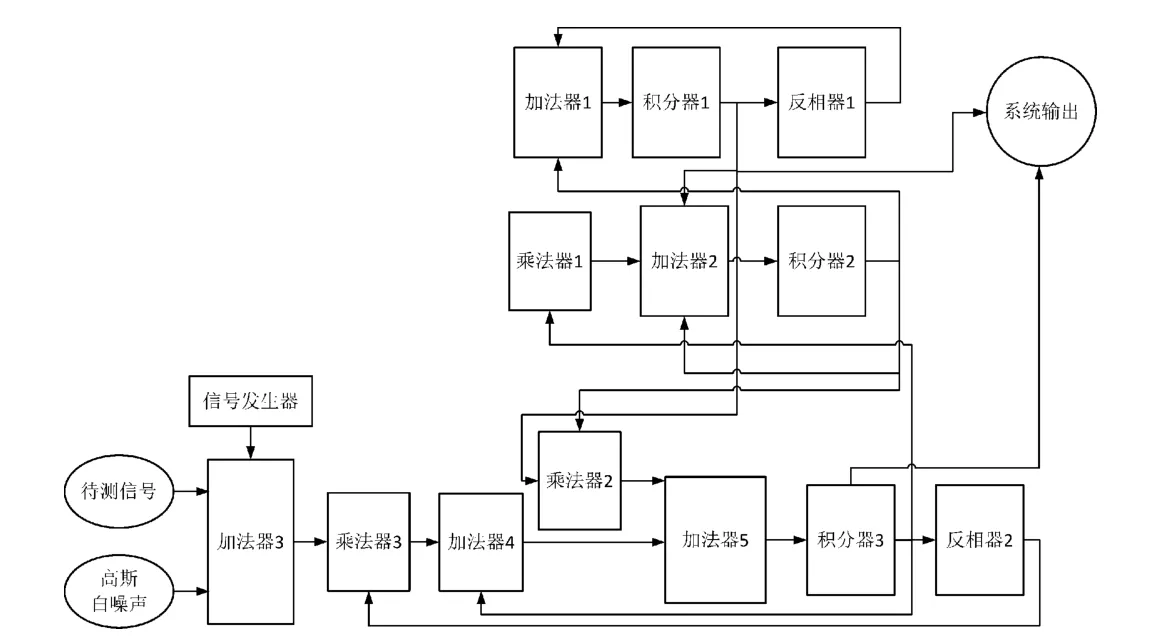
图4 混沌系统检测具体原理图
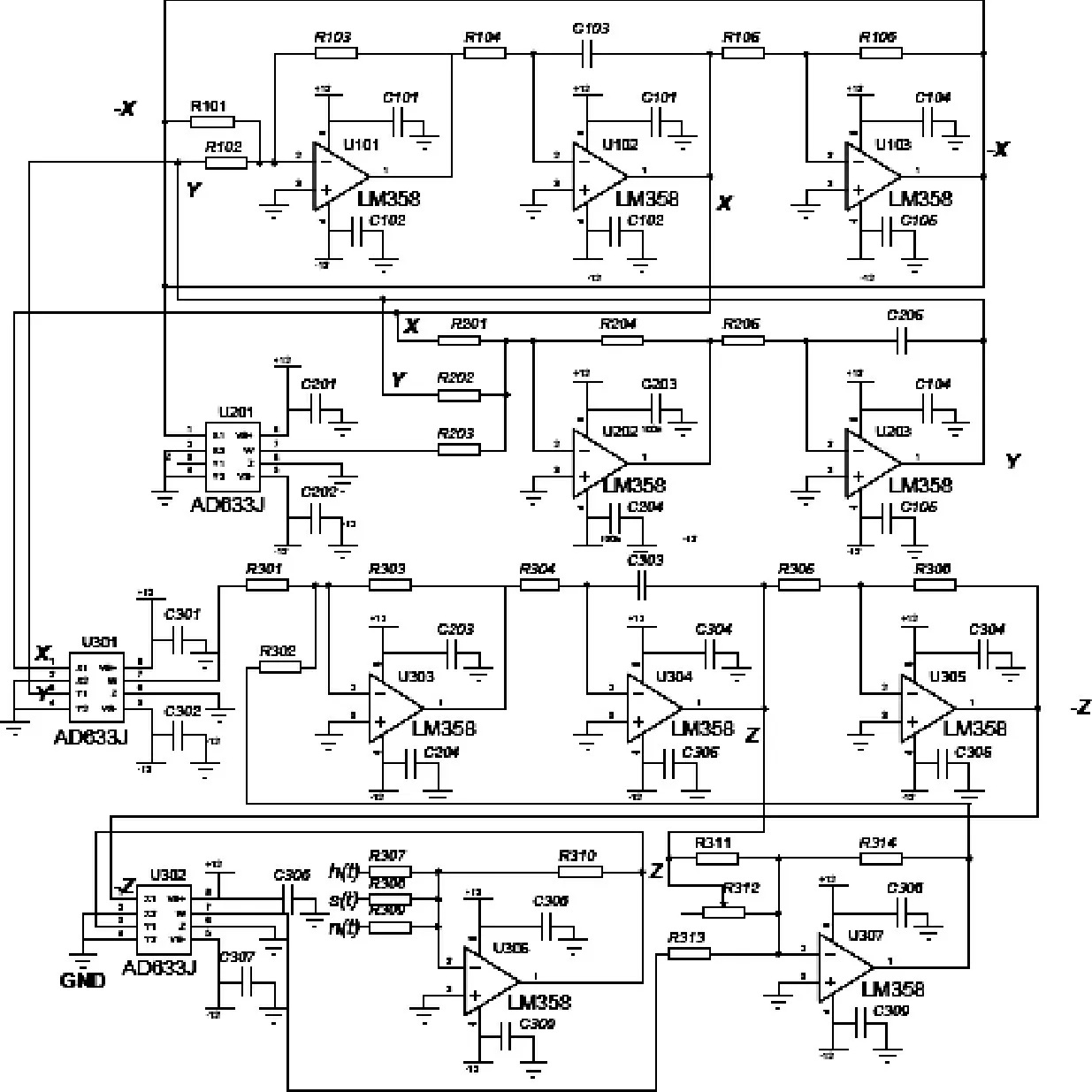
图5 混沌检测电路
根据式(1)所示类Lorenz系统微分方程,并结合图5中电路系统参数,列出系统状态方程:

将第一运算放大器U102的7 脚输出电压X和第四运算放大器U304的1 脚输出电压Z 这两个值的输出在示波器上的轨迹就是本文所用的类Lorenz系统相平面x-z 上的轨迹。系统参数m 由m =确定,通过改变滑动变阻器R312的大小值,可将系统控制在不同的周期态和混沌态下。
3.2 微弱正弦信号检测实验
由于实验仪器精度的限制,所以在具体实验中,将噪声强度、信号幅值等参数都相对于仿真参数放大了10倍。
调整R312,将控制信号h(t)=rcos(ωt)幅值r 调整到0.01 V,f =1 Hz 使得系统被控制在混沌临界状态,如图6(a)所示。将功率为0.001 W的高斯白噪声信号功率加入到系统中,系统输出x-z 相图,如图6(b)所示。从示波器的相图中可以很明显地看到对比系统处于临界状态的相图更加粗糙,但是并没有改变系统的混沌状态。
入微弱正弦信号s(t),频率与控制信号h(t)同频率,fs=f=1 Hz,rs由0 开始增大过程中,当rs达到0.000 3 V时,系统状态发生了明显的变化,由混沌状态转变为周期二状态,示波器输出x-z 相平面如图6(c)所示。

图6 频率为1 Hz时的微弱正弦信号检测示意图
从上述微弱信号检测示意图分析可以发现,系统混沌状态将出现在控制信号的频率与微弱正弦信号的频率不相等时,而当控制信号的频率与微弱正弦信号的频率相等时,系统就进入大尺度周期态。因此,可以通过调节控制信号的频率,检测出待测信号中含有的各种微弱正弦信号的频率。通过实验得到此检测系统的最低门限约为rs=0.003 V,最高为0.146 V,根据信噪比公式计算出信噪比为SNR =10lg(r2/2P)=-23.47 dB。电路实验证明了利用正弦控制信号来检测微弱周期信号是可行的,且易于实现。
4 结束语
本文根据特定混沌系统对于参数敏感性而对噪声免疫的特性,利用双参数控制方法,构造了类Lorenz系统的微弱信号检测模型,理论分析了本检测系统具有检测中低频微弱周期信号的特性,并通过仿真实验及混沌检测电路实验,实现了噪声背景下对微弱信号的检测,验证了系统的可行性。今后将在基于混沌理论的微弱信号检测的电路实施方面做进一步的探索和研究。
[1]谌龙,王德石,史跃东.基于受控Lorenz系统的微弱脉冲信号检测[J].仪器仪表学报,2010,8(1):48-52.
[2]Ott E,Grebogi C,Yorke J A.Controlling chaos[J].Physical review letters,1990,64 (11):1196-1199.
[3]Romeriras F J,Grebogi C,Ott E.Controlling chaotic dynamical systems[J].Physica D:Nonlinear Phenomena,1992,58(1):165-192.
[4]Di Bernardo M.A purely adaptive controller to synchronization and control chaotic system[J].Physics Letters A,1996,214(3):139-144.
[5]王永生,姜文志,赵建军,等.一种Duffing 弱信号检测新方法及仿真研究[J].物理学报,2008,57(4):2053-2059.
[6]Sauer T.A noise reduction method for signals from nonlinear systems[J].Physica D:Nonlinear Phenomena,1992,58(1):193-201.
[7]Walker D M,Mess A I.Noise reduction of chaotic systems by Kalman filtering and by shadowing[J].International Journal of Bifurcation and Chaos,1997,7(3):769-779.
[8]李月,杨宝俊,林红波,等.基于特定混沌系统微弱谐波信号频率检测的理论分析与仿真[J].物理学报,2005,54(5):1994-1999.
[9]王林泽,高艳峰,李子鸣.基于新蝶状模型的混沌控制及其应用研究[J].控制理论与应用,2012,29(7):915-920.
[10]赵文礼,黄振强,赵景晓.基于Duffing 振子的微弱信号检测方法及其电路的实现[J].电路与系统学报,2011,16(6):120-124.
[11]Wolf A,Swift J B,Swinney H L,et al.Determining Lyapunov exponents from a time series[J].Physica D:Nonlinear Phenomena,1985,16(3):285-317.
[12]Matías M A,Güémez J.Stabilization of chaos by proportional pulses in the system variables[J].Physical review letters,1994,72(10):1455-1464.
