基于ELM和振动信号的高压断路器机械故障诊断

刘 艳，陈丽安

LIU Yan, CHEN Li-an

（厦门理工学院 福建省高电压技术重点实验室，厦门 361024）

0 引言

高压断路器是电网中起保护和控制作用的重要电力设备，其运行状态和电网的稳定息息相关，因此，对于断路器的故障诊断有着重要意义[1]。其中，基于振动信号的断路器机械故障诊断已经取得了较多成果，其故障特征提取方法包括：短时傅里叶变换提取特征量[2]；高阶谱分析提取特征量[3]；小波包-特征熵提取特征量[4]；小波包特征节点最大系数提取特征量[5]；经验模态分解能量熵提取特征量[6]；希尔伯特变换提取振动信号零相位滤波时频熵作为特征量[7]等。以上方法都仅提取振动信号的一类特征量，为了综合反映断路器的机械运行状态，本文提出了使用两种特征提取方法共同提取振动信号特征，将不同特征的信息融合作为断路器的故障诊断依据。此外，鉴于断路器的某些故障（如：缓冲器失效）仅对断路器的分闸过程产生影响，为了更好地对断路器开断时的机械状态进行监测，本文选取断路器分闸过程的振动信号作为特征样本。

在人工智能算法的选取方面，目前常见的算法有：传统神经网络（如BP神经网络）和支持向量机。传统的神经网络虽然具有较好的泛化能力和抗噪性，但是训练时需要大量的样本[8]，实际操作中断路器不宜长期在故障状态下动作，可获取的故障状态训练样本不大，故传统神经网络不能满足断路器的小样本分类；SVM支持向量机训练过程中有较多的参数需要设置[9]；小样本分类算法中，SOM网络训练样本数少，需要确保训练样本的典型性才能使网络具有良好的泛化能力[10]。本文提出使用ELM极限学习机的人工智能网络进行分类，训练样本数可根据具体情况设置，且该种网络随机产生隐含层神经元阈值以及输入层和隐含层之间的连接权值，训练过程中无需调整，学习效率快、泛化性能好[11]。通过实验验证，该种故障诊断方法具有良好的分类效果。

1 特征量的提取

1.1 Hilbert边际谱能量

信号经过HHT变换（Hilbert-Huang Transform，希尔伯特黄变换）可以得到瞬时频率和瞬时幅值，即表示出信号完整的时间-频率分布，进一步将Hilbert谱对时间积分，得到Hilbert边际谱，从统计学意义上表示出整个信号每个频率点的积累幅值分布[12～14]。因此，Hilbert边际谱更能反映非平稳信号的特点。

能量是振动信号的一个重要特征，能够反映机械运动的状态：机械部件发生变化时，振动信号的各个频率成分也会产生变化，而同一频率带内信号能量的变化会更加明显[15]。

Hilbert边际谱总能量E(w)定义如下：

式(1)中，h(w)为信号的希尔伯特边际谱，n为信号总长度。由该式可知，Hilbert边际谱能量将Hilbert边际谱经过平方处理，使得信号的强弱对比度进一步增大，即高频冲击信号代表的信号成分更加强烈，比重更大；而噪声产生的影响可进一步削弱。

1.2 振动信号的Hilbert边际谱分析

正常状态（T1）、缓冲器失效状态（T2）、分闸不到位状态（T3）和分闸弹簧失效状态（T4）振动信号的频域分布如图1～图4所示。

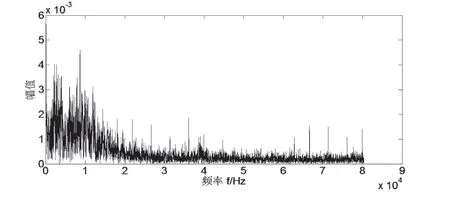
图1 正常状态分闸频域

图2 缓冲器失效状态分闸频域

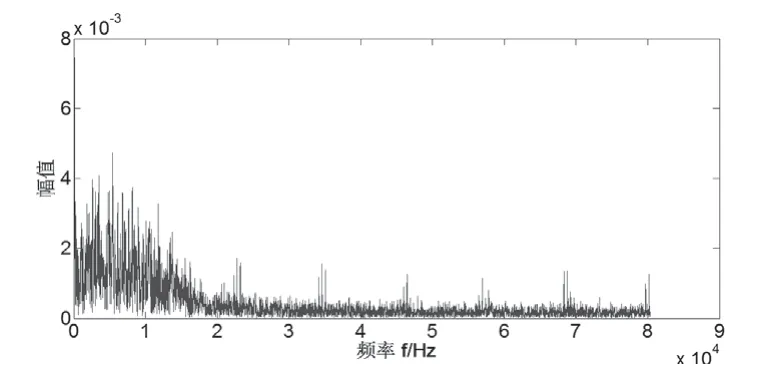
图3 分闸不到位状态分闸频域

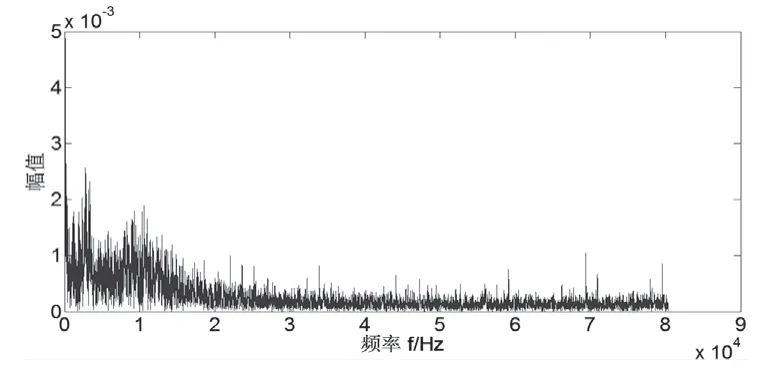
图4 分闸弹簧失效状态频域

表1 断路器四类状态的频域特点

取一组正常振动信号进行EMD分解，得若干组IMF（intrinsic mode function），不同的IMF代表原始信号中的不同频率段，分别求前8组IMF各自的频谱，如图5所示。

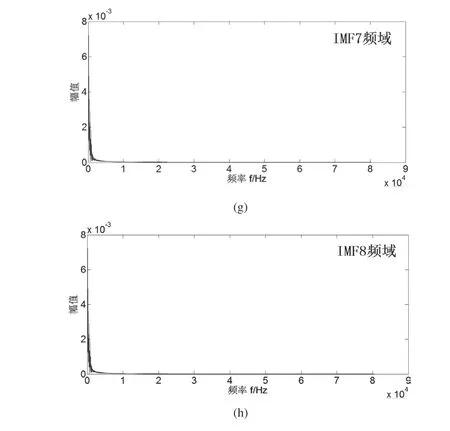
图5 IMF1～IMF8频域

由图5可知，断路器分闸振动信号分解得的IMF1至IMF8反应了振动信号由高频段到低频段的情况。结合前文可知，区分不同状态下振动信号频域分布的成分主要集中在高频段（IMF1～IMF4）信息，故选取IMF1、IMF2、IMF3、IMF4四组固有模态分量作为特征提取对象，以四组固有模态分量各自能量占4个能量总和的比例作为衡量频率分布差异的方法。此外，为了有效区分正常状态（T1）和分闸弹簧失效状态（T4）这种分布比例具有相似性，幅值差异大的故障类别，将振动信号总能量一同作为特征值。

1.3 振动信号样本库的建立

表2列举了正常状态（T1）、缓冲器失效状态（T2）、分闸不到位状态（T3）以及分闸弹簧失效状态（T4）下，12kV真空断路器经过多次实验得到的振动信号特征量典型值。前四列数据依次代表振动信号经过EMD分解后得到的IMF1、IMF2、IMF3、IMF4四个固有模态分量各自能量占四组能量和的比例，第五列列举了该样本信号总能量。

将表2故障诊断知识库里四种状态的前4个特征值，即IMF1、IMF2、IMF3、IMF4四个固有模态分量能量占其能量和的各自比例的典型值整理成饼状图，如图6所示；将四种状态的第五个特征值，即振动信号总能量整理成柱形图进行对比，如图7所示。

图6 四种状态断路器IMF1～IMF4能量比例

从图6可看出，正常状态（T1）、缓冲器失效状态（T2）、分闸不到位状态（T3）三种情况下，IMF1、IMF2、IMF3、IMF4四个固有模态分量能量占其能量和的各自比例具有明显的区别；分闸弹簧失效状态（T4）与正常状态（T1）下的断路器的IMF1、IMF2、IMF3、IMF4四个固有模态分量能量占其能量和的比例具有类似性。

图7 四种状态断路器振动信号总能量

图7可知，四种状态的总能量值相互存在差异，可以辅助IMF1、IMF2、IMF3、IMF4四个固有模态分量能量占其能量和的比例分布，对断路器进行机械故障诊断。

表2 故障诊断知识库

2 ELM极限学习机

ELM网络结构如图8所示，其中ω代表输入层与隐含层神经元间的连接权值；β代表隐含层与输出层神经元间的连接权值。

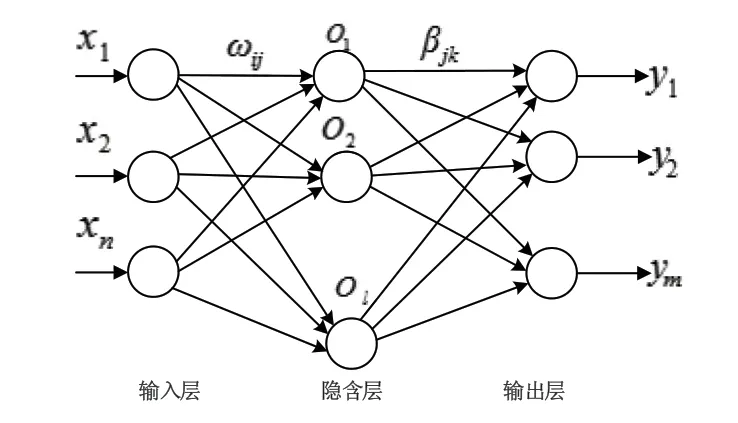
图8 典型单隐含层前馈神经网络结构

2.1 构建ELM极限学习机网络

1）确定输入层节点数和输出向量

输入层节点数与样本的维数直接相关，与影响的特征数相同，本文提取的特征数据有5个：IMF1、IMF2、IMF3、IMF4四个固有模态分量能量占其能量和百分比以及振动信号的总能量。待分类状态有以下四类：正常状态（T1）、缓冲器失效状态（T2）、分闸不到位状态（T3）以及分闸弹簧失效状态（T4），故ELM网络的输入节点数I=5×4=20个。输出向量为四种状态的分类标签：1、2、3、4分别代表正常状态、缓冲器失效状态、机构卡涩状态和分闸弹簧失效状态。

2）确定隐含层节点数

隐含层节点数受到输入输出层节点数影响，节点数过少会影响训练精度；反之，训练次数过多则会使控制过程复杂化，导致训练结果不够精确，一般取小于训练样本数的正数作为隐含层节点数[16]。

2.2 极限学习机ELM网络的训练

极限学习机ELM网络的训练步骤如下[17]：

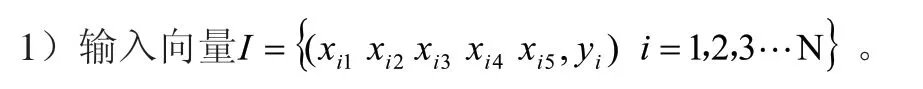
其中，xil～xi5分别为第i组振动信号分解得IMF1、IMF2、IMF3、IMF4四个固有模态分量能量占其能量和的比例以及该振动信号的总能量；yi为第i组特征量对应的状态类型。

2）设定初始隐含层节点数Q和训练样本数量N，利用步骤1）中输入的样本训练ELM网络，确定网络的权重参数。

3）随机选择隐含层节点偏移值bi和输入连接权值ai，因为隐含层节点为可加性的，所以选择sigmoid函数作为激活函数。

4）计算隐含层节点输出矩阵H，按照公式：

将aibixi代入式(3)计算隐含层节点输出矩阵H。

5）选取最小二乘估计的β=(HTH)-1HTT为迭代初始值，求得网络的输出权重βi。

6）将xi输入已知权重参数 (ai，bi，βi)的ELM网络，得到训练结果Ti为：

计算训练样本的输出误差为：

7）网络训练根据输出误差来适当增加或减少隐含节点数，寻求合适的隐节点数。当误差大于允许范围就增加节点数，反之减少节点数。重复步骤3）～步骤7），直到训练样本的误差小于10%，训练完后，保存网络的输出权重。

3 故障诊断实验和结果分析

利用1.3节建立的振动信号特征量知识库里分闸过程的四个状态（正常状态、缓冲器失效状态、分闸不到位状态和分闸弹簧失效状态）各选取30个样本作为断路器分闸过程故障诊断ELM网络模型的训练样本，训练样本编号及分类标签如表3所示。结合2.1节设置的参数及2.2节ELM网络的训练步骤，进行分闸过程ELM网络的训练，随后利用训练所得ELM网络模型对40组预测样本进行状态分类，用于分类的预测样本编号及期望分类标签如表4所示。

表3 分闸过程训练样本编号及分类标签

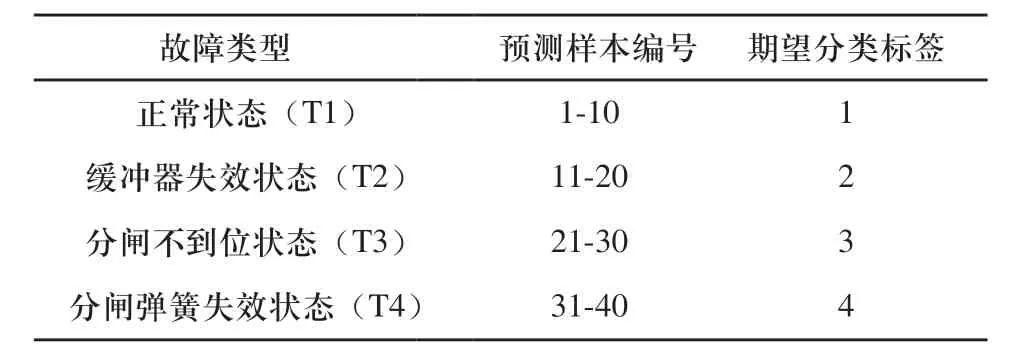
表4 分闸过程预测样本编号及期望分类标签

由2.1节知：隐含层节点数G受到输入输出层节点数影响，则通过对该参数的不同赋值，进行对比分析。

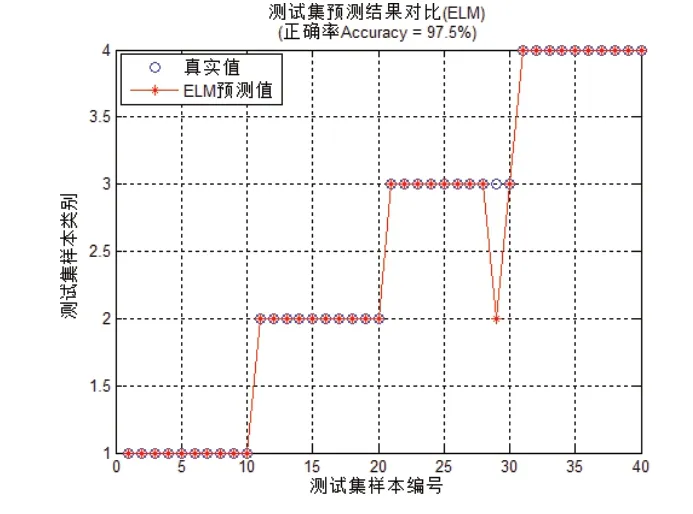
图9 Q=8时预测情况

图10 Q=15时预测情况

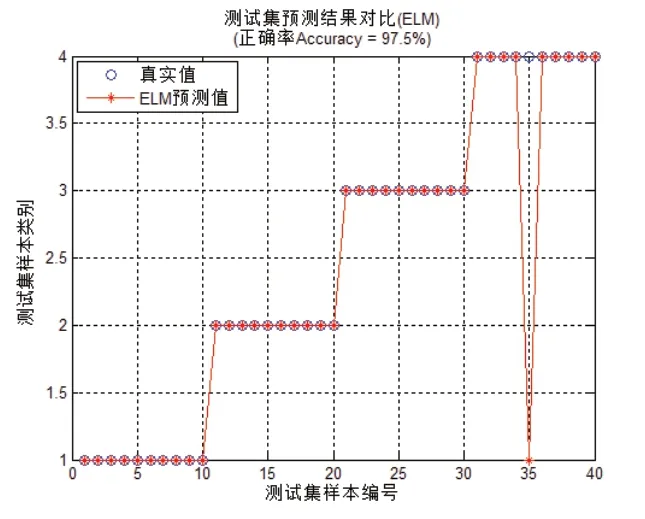
图11 Q=20时预测情况

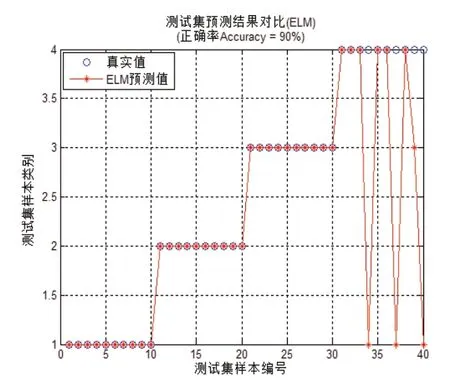
图12 Q=80 时预测情况

由图9～图12可知：当隐含层神经元个数得到恰当赋值，如图10中Q=15时，训练得到的ELM模型可以零误差逼近所有训练样本。然而，并非隐含层神经元个数越多越好，如图12所示，将隐含层神经元个数增加至80，预测率反而大大下降。综上可知，分闸过程使用的ELM网络训练过程中，隐含层神经元个数Q设置为15时，应用样本库里的预测样本可以达到100%准确分类。

4 结束语

本文提出了一种基于振动信号的高压断路器故障诊断的新方法，与现有的基于振动信号的高压断路器故障诊断方法相比，该方法具有如下优点：

1）提出了结合固有模态边际谱能量比例和振动信号总能量共同作为故障特征提取对象的信息融合诊断方法，更加全面反映断路器的真实状态。

2）采用极限学习机进行故障分类，避免了传统神经网络需要庞大的数据信息作为训练样本的需求，以及SVM支持向量机使用过程中需要设置众多参数的不便。

经过实验验证，该方法对本文使用的样本库进行分类，准确率可以达到100%，具有良好的工程应用价值。

[1]段传宗,鄢志平,鄢志辉.高压断路器故障检测与诊断技术[M].北京:中国电力出版社,2014:9-12.

[2]Hoidalen H.K.,Runde M.Continuous monitoring of circuit breakers using vibration analysis[J].IEEE Transactions on Power Delivery,2005,20(4):2458-2465.

[3]董越,肖登明.基于WP-AR模型的双谱估计在高压断路器振动信号处理中的应用[J].高压电器,2009,45(4):137-141.

[4]钟建英,刘洋,林莘,等.基于振动信号特征的高压断路器机械故障诊断技术研究[J].高压电器,2013,49(9):49-54.

[5]孙来军,胡晓光,纪延超.一种基于振动信号的高压断路器故障诊断新方法[J].中国电机工程学报,2006,26(6):157-161.

[6]黄建,胡晓光,巩玉楠.基于经验模态分解的高压断路器机械故障诊断方法[J].中国电机工程学报,2011,31(12):108-113.

[7]常广,王毅,王玮.采用振动信号零相位滤波时频熵的高压断路器机械故障诊断[J].中国电机工程学报,2013,33(3):155-162.

[8]胡汉梅,鲍亮亮,赵海军.神经网络在变压器故障诊断中典型算法研究[J].高压电器,2008,44(3):217-220.

[9]张静.基于SOM的变压器故障诊断研究[J].电力学报,2014,29(4):318-321.

[10]袁金丽,李奎,郭志涛,等.基于SVM与合分闸线圈电流参数的高压断路器机械故障诊断[J].高压电器,2011,47(3):26-30.

[11]史峰,王小川.Matlab神经网络30个案例分析[M].北京:北京航空航天大学出版社,2010:297-300.

[12]韩清凯,于晓光.基于振动分析的现代机械故障诊断原理及应用[M].科学出版社,2010:81-82.

[13]褚福磊,彭志科,冯志鹏,等.机械故障诊断中的现代信号处理方法[M].科学出版社,2009:113-124.

[14]何正嘉,陈进,王太勇,等.机械故障诊断理论及应用[M].高等教育出版社,2010:74-81.

[15]叶吉祥,胡海翔.Hilbert边际能量谱在语音情感识别中的应用[J].计算机工程与应用,2014,50(7):203-207.

[16]齐郑,张惠汐,饶志,等.基于极限学习机的多信息融合区段定位方法[J].电力系统保护与控制,2014,42(19):74-80.

[17]王小川,史峰,郁磊.MTLAB43个神经网络案例分析[M].北京:北京航空航天大学出版社,2013.