大型薄壁回转结构件加工变形预测研究

郑耀辉 ，王江涛，王明海,2，李晓鹏，王 奔 ZHENG Yao-hui , WANG Jiang-tao, WANG Ming-hai,2, LI Xiao-peng, WANG Ben

（1.沈阳航空航天大学 航空制造工艺数字化国防重点学科试验室，沈阳 110136；2.北京航空航天大学 能源与动力工程学院，北京 100191）

0 引言

随着我国航空事业的快速发展，航空制造业对零件的使用性、安全性、环保性等各方面性能的要求不断提高。为了提高推重比，飞机零部件广泛使用薄壁整体结构件，然而这类薄壁件尺寸大，刚性差，在加工过程中容易变形而难以满足加工要求，影响零件的使用性能乃至飞机服役寿命。对此，国内外研究人员对薄壁件的加工变形机理，变形规律和控制及补偿策略等问题，进行了大量的试验和仿真研究[1]。K.Rai[2]基于三维铣削模型，研究了薄壁隔板不同工装、走刀路径、铣削参数下的加工变形。S.Ratchev[3]考虑了仿真过程中不同刀具点位置的误差并采用NC代码建立了补偿机制。武凯[4]在得到薄壁腹板加工变形基本规律的基础上，提出了以大切深和分布环切法增强薄壁件刚度，减小变形量。尹飞鸿[5]针对航空薄壁框类零件，研究切削力对加工变形量的影响，预测了不同尺寸框类零件的加工变形规律。周孝伦[6]、秦国华[7]分别基于遗传算法和数学模型，讨论了装夹方案对工件变形的影响，提出了同步优化夹具布局和夹紧力的方法，优化了加工过程中工件的弹性变形。

然而，这些关于加工变形的研究多是针对板类薄壁结构件局部部位的理论分析，对于大尺寸结构件的整体变形情况还不能做出预测，尤其是对航空发动机中广泛采用的薄壁回转体零件的加工变形问题的研究还不够。刘海涛[8]应用单元生死技术模拟了薄壁回转体的加工变形，但其研究更侧重于初始残余应力对变形的影响，对影响加工变形的因素研究还不全面。

针对现有加工变形问题研究中的不足，本文基于机匣类零件建立了全尺寸大型薄壁回转体三维有限元模型，通过所开发的载荷施加/卸载辅助软件完成了车削切削力的动态加载和卸载，实现了薄壁回转体的整体变形预测，并研究了两种辅助支撑条件下切削力对加工变形的影响规律。

1 有限元仿真模型的建立

1.1 工件模型的建立

机匣零件的加工质量对航空发动机的装配和使用性能都起着关键作用，其制造水平也是制约发动机制造技术的关键因素。机匣零件的一般加工顺序为粗车大小端、半精车大小端、精车大小端、钻孔、铣花边及槽。通过对工序的分析可知，粗车和半精车工序加工余量相对较大，工件刚性强，而精车工序余量小，精车完成后机匣壁厚只有1.5mm～2.5mm，是车削变形的主要阶段，因此选择对精车过程建立仿真模型。由于钻孔、铣花边在车削工序之后，且去除量小，对此模型可以做相应的简化处理。

所建立的精车加工装配三维有限元模型如图1所示。工件高90mm，其中小端高40mm，大端高50mm，最小圆柱半径395.5mm，最大圆柱半径428.5mm，大、小端壁厚均为1.5mm。

图1 工件三维有限元模型

机匣加工所用材料为GH4169高温合金，材料本构模型为J-C模型，模型参数如表1所示。

表1 GH4169本构模型参数

1.2 切削力的获取和施加

切削力的值由经验公式计算得出，由GH4169高温合金车削试验得到的车削切削力经验公式如式(1)所示。

为了快速获取不同切削参数下的切削力大小，将切削力计算公式写入程序源代码，开发了车削力计算功能模块。如图2软件界面左侧所示，输入不同的切削速度、进给量、切削深度，点击“计算切削力”即可计算出不同切削参数下的三向切削力大小。

为了施加某一工步的切削力载荷，首先定义该工步的走刀轨迹，在Abaqus中建立走刀轨迹的节点集合，提取出包含节点信息的文件，然后应用所开发的载荷施加/卸载辅助软件识别文件并读取节点信息，以指定的节点数量为步长，自动创建多个有限元分析步。运行脚本文件，在相应的模型中生成分析步和载荷，从而实现该工步切削力的动态加载和卸载。该工步完成后，用Abaqus自带的“单元生死”功能，去除该工步需要切除的材料。然后进行下一工步的分析计算，以此循环直至完成整个精加工过程。

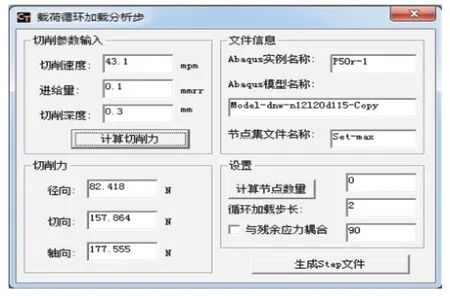
图2 移动载荷施加/卸载软件界面

1.3 装夹方式

工件的装夹方式是影响薄壁件加工变形的重要因素，最高占引起加工误差因素的60%[9]。对于机匣类大型薄壁件，采用立车加工。车削过程中，用专用夹具压紧花边，采用径向辅助支撑以增强车削过程中工件的刚性。整套辅助支撑分为内支撑和外支撑，当车削内圆柱表面时，外侧支撑顶住外圆柱表面以抑制工件变形，同理，车削外表面时，内侧支撑起作用。

1.4 仿真试验方案

在工件材料和几何形状已确定的情况下，切削力和装夹方案是影响加工变形的关键因素[10]，因此以切削力和辅助支撑数目为影响因素设计仿真试验方案。辅助支撑元件的数目采用生产中常用的24个和12个，元件长度为20mm，切削力的设置如表2所示。

表2 切削力设置表

2 仿真结果分析

2.1 仿真结果分析

按照上述试验方案进行仿真计算，由仿真结果得到不同方案下的内圆径向跳动、外圆径向跳动及支撑元件反作用力大小，作为评估加工变形大小及选择仿真方案的依据。

2.1.1 支撑元件数量为24个

支撑元件数量为24个时，仿真试验得到的内圆径向跳动最大误差、外圆径向跳动最大误差及支撑元件最大反作用力如表3所示。

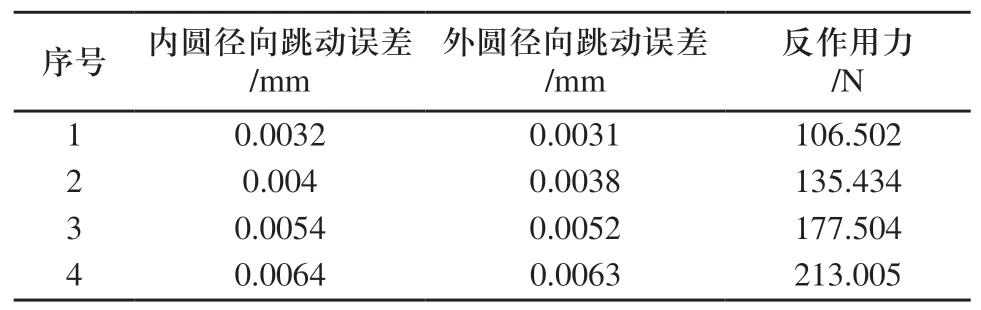
表3 最大径向跳动误差及反作用力（24支撑）

根据仿真试验数据，支撑元件数量为24个时，建立的切削力与内圆径向跳动最大误差、外圆径向跳动误差关系曲线如图3所示，切削力与支撑元件最大反作用力关系曲线如图4所示。

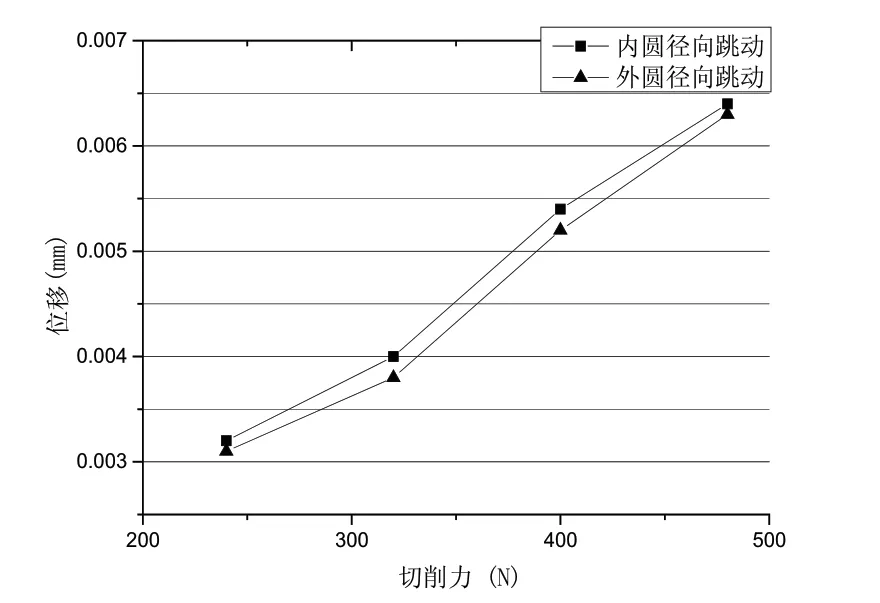
图3 切削力与跳动误差关系图（24支撑）

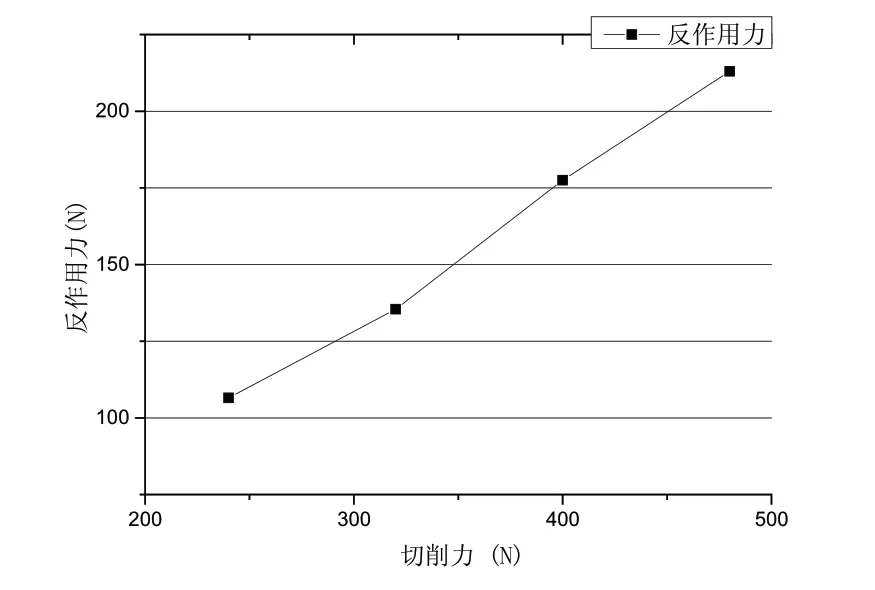
图4 切削力与反作用力关系图（24个支撑）

2.1.2 支撑元件数量为12个

支撑元件数量为12个时，仿真试验得到的内圆径向跳动最大误差、外圆径向跳动最大误差及支撑元件最大反作用力如表4所示。

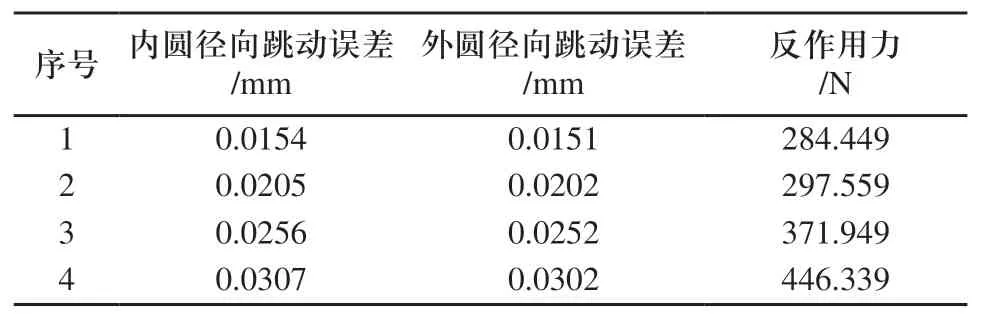
表4 最大径向跳动误差及反作用力（12支撑）

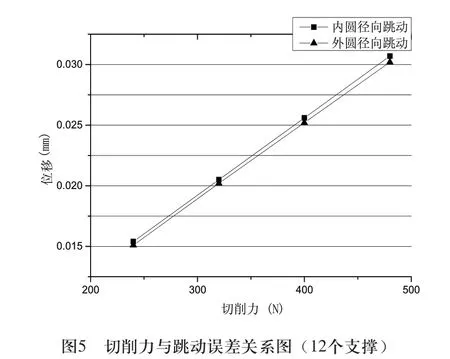
根据仿真试验数据，支撑元件数量为12个时，建立的切削力与内圆径向跳动最大误差、外圆径向跳动误差关系曲线如图5所示，切削力与支撑元件最大反作用力关系曲线如图6所示。

图6 切削力与反作用力关系图（12个支撑）

2.2 变形规律分析

在24个辅助支撑元件条件下，随着切削力的增大内圆径向跳动误差最小值和最大值分别为0.0032mm和0.0064mm，外圆径向跳动最小值和最大值分别为0.0031mm和0.0063mm，对比可知，内圆跳动与外圆跳动变化规律一致，且数值相差不到2%。这可能是因为由于薄壁件壁厚仅1.5mm，而内圆和外圆的半径尺寸都将近400mm，1.5mm的尺寸差距相对很小，所以内圆和外圆的变形规律十分相似。从图4可以看出，当支撑元件数量为24个时，随着切削力的增加，支撑元件最大反作用力均增大，而且基本成线性规律增大；从图6可以看出，支撑元件数量为12个时，随着切削力的增加，支撑元件最大反作用力增大，切削力超过330N后，基本成线性规律增大。更具体的对比可以看出，无论支撑元件数目是24个还是12个，支撑元件的反作用力大小总是跟随着切向力大小增大而增大。

进一步对比不同辅助支撑数目时的变形量却发现差别很大：24个和12辅助支撑元件条件下的最小变形量分别为0.0031mm和0.0151mm，最大变形量分别为0.0064mm和0.0307mm。这说明增加辅助支撑的数目可以有效的减小加工变形，仿真试验数据表明，辅助支撑数目由12个增加到24个时，变形量提高了一个数量级。但这并不能说辅助支撑数目越多越好，因为对于大型整体薄壁件，其装夹过程比较复杂，增加辅助支撑数目必然增加工件装夹时间，影响加工效率。另外，按照加工工艺要求，精加工阶段材料去除率低，背吃刀量小，因而切削力较小，精加工内圆和外圆产生的最大跳动误差为0.0307mm，相对于对应工艺的公差要求0.1mm，形位误差值还是可以接受的。

由以上分析可知，可以根据不同切削力情况的最大变形量和辅助支撑反作用力大小调节辅助支撑数目，在保证加工精度的前提下，减少装夹时间，提高生产效率。

3 试验验证

3.1 试验测量方法

通过对比相同仿真和试验条件下内、外圆径向跳动误差值，验证仿真结果的准确性。仿真条件下，可以在自定义的柱坐标下，直接查询节点的径向位移以确定变形量。而试验条件下并没有明确的坐标参考，因此选取内、外圆周上任一位置为零点，然后依次等角度测量8个点的相对径向位移误差，变形量测量点位置分布示意图如图7所示。

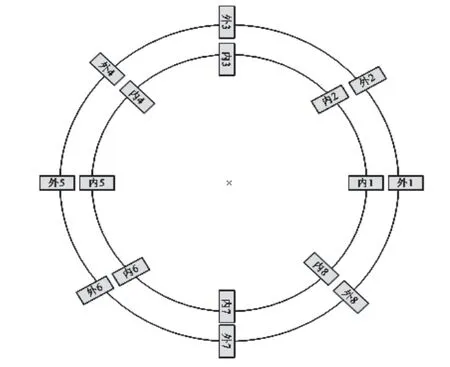
图7 测量位置分布图

3.2 试验与仿真结果对比

按照上述方法，测量出12个辅助支撑条件下精加工后，内、外圆8个位置点的变形量值。同样的条件下，测量出仿真结果中相对应的8个位置点的变形量。得到的原始数据结果如表5所示。

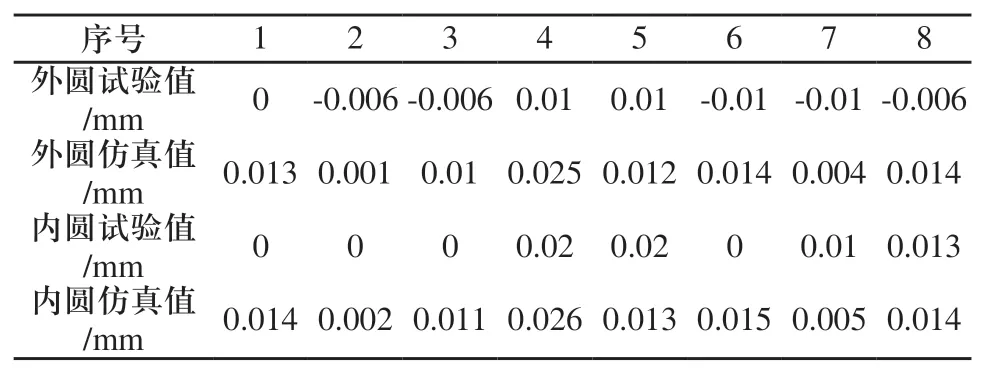
表5 变形量原始数值

由于试验和仿真数据获得方法不一致，将试验数据转换后与仿真数据对比，然后绘制在同一图表中，得到如图8所示。

图8 仿真和试验变形趋势图

通过试验结果可以看出，工件的变形量先增大，后减小，再增大，总体表现为震荡波动，这可能是由测量点和辅助支撑的相对位置决定的。对比试验和仿真的变形曲线可以看出，试验测得的内、外圆变形量试验和仿真曲线变化趋势一致，这也验证了试验得出的结论。试验和仿真结果的最大变形量分别为0.02mm和0.026mm，考虑到试验中力的波动以及其他加工工序对变形量的影响，仿真结果可以接受。对比试验内、外圆的变形曲线，可以看出内、外圆径向变形量大小和变化趋势都一致，和文中第二部分分析一致，这也进一步表明仿真结果比较可靠，该仿真模型可以用于预测工件加工变形规律。

4 结论

通过对薄壁回转体车削模型的研究和加工变形规律的分析，可以得出以下结论：

1）本文应用的动态载荷施加/卸载方法，是预测大型薄壁回转体整体加工变形的一种有效方法，建立的有限元仿真模型可以作为研究加工变形问题的基础模型。

2）通过对精加工工序不同切削力和支撑条件下的变形量分析可知，薄壁件的圆柱度误差随着切削力的增加而增大，辅助支撑元件的反作用力随着切削力的增加初始增幅较缓慢，而当支撑反作用力超过330N以后，基本线性增大。

3）薄壁件的加工变形是一个复杂的问题，对于影响加工变形的每个因素都需要更深入的研究。本文仅探讨精加工阶段切削力和两种辅助支撑元件数目条件下薄壁件的加工变形规律，对于影响切削力大小的每个切削参数、辅助支撑元件的位置、辅助支撑元件的长度以及其他加工工序、不同材料去除率等条件下的加工变形问题，都需要做进一步的研究。

[1]刘维伟,张定华,史耀耀,等.航空发动机薄壁叶片精密数控加工技术研究[J].机械科学与技术,2004(03):329-331.

[2]Rai J K,Xirouchakis P.Finite element method based machining simulation environment for analyzing part errors induced during milling of thin-walled components[J].International Journal of Machine Tools and Manufacture.2008,48(6):629-643.

[3]Ratchev S,Liu S,Huang W,et al.An advanced FEA based force induced error compensation strategy in milling[J].International Journal of Machine Tools and Manufacture.2006,46(5):542-551.

[4]武凯,何宁,廖文和,等.薄壁腹板加工变形规律及其变形控制方案的研究[J].中国机械工程,2004(08):14-18.

[5]尹飞鸿,唐国兴,陈志伟,等.铝合金航空薄壁框铣削变形预测研究[J].制造业自动化,2012(18):34-36.

[6]周孝伦,张卫红,秦国华,等.基于遗传算法的夹具布局和夹紧力同步优化[J].机械科学与技术,2005(03):339-342.

[7]秦国华,吴竹溪,张卫红.薄壁件的装夹变形机理分析与控制技术[J].机械工程学报,2007(04):211-216.

[8]刘海涛.精密薄壁回转体零件加工残余应力及变形的研究[D].哈尔滨工业大学,2010.

[9]Li B,Melkote N.Improved workpiece location accuracy through fixture layout optimization[J].In ternational Journal of Machine Tools &Manufacture.1999(39):871-883.

[10]董辉跃,柯映林.铣削加工中薄壁件装夹方案优选的有限元模拟[J].浙江大学学报(工学版),2004(01):18-22.