扫地机器人车轮打滑检测与修正研究

李泉溪，赵帅鹏，武文琪

LI Quan-xi, ZHAO Shuai-peng, WU Wen-qi

（河南理工大学 计算机科学与技术学院，焦作 454003）

0 引言

扫地机器人工作时，存在因车轮打滑引起运行方向改变的问题，这会降低扫地机器人清扫覆盖率并增长清扫时间[1]。目前，人们使用电子罗盘或三轴陀螺仪检测因车轮打滑引起的运行方向误差，但电子罗盘容易受外部磁场干扰，三轴陀螺仪存在漂移误差，对长时间运行产生的小角度方向误差检测灵敏度低等问题[2]。本文通过研究各个车轮的光耦输出脉冲数之间的关系，设计了双轮检测系统。该系统能够准确累计运行方向误差，提高了方向误差检测精度，抗干扰能力强，易于实现。

1 双轮检测系统总体设计

双轮检测系统的组成主要包括：驱动轮、检测轮、减速器、光耦、测速片、电机，结构图如图1所示。车轮X1，X2为驱动轮；Y1，Y2为检测轮，检测轮依靠车轮与地面的摩擦力转动。

双轮检测系统的控制由处理器实现，处理器完成的主要任务有：计算光耦输出脉冲数、运行状态判断、方向误差计算、电机转动方向控制。扫地机器人左转弯由反向驱动X1正向驱动X2实现；右转弯由反向驱动X2正向驱动X1实现[3]。

图1 双轮检测结构

2 运行状态分析

扫地机器人正常运行有四种状态：前进；后退；左转；右转[4]。正常运行状态根据电机转动方向判断[5]。车轮打滑有三种状态：左车轮打滑；右车轮打滑；两个车轮都打滑。处理器对打滑状态的判断顺序为：先判断是否存在左车轮打滑或右车轮打滑，再判断是否存在两个车轮都打滑。

扫地机器人运行时，每隔时间Δt，处理器计算车轮Y1与Y2的光耦输出脉冲数差值，其值为：

式中，Q1、Q2分别指车轮Y1、Y2的光耦输出脉冲数。若ΔQ大于0，说明左驱动轮打滑，扫地机器人运行方向向左偏转；ΔQ小于0，说明右驱动轮打滑，扫地机器人运行方向向右偏转。

在Δt内，若因驱动轮打滑，扫地机器人运行方向向右偏转，在直行和转弯两种正常运行状态下，判断是否存在两个车轮都打滑的判定式分别为：

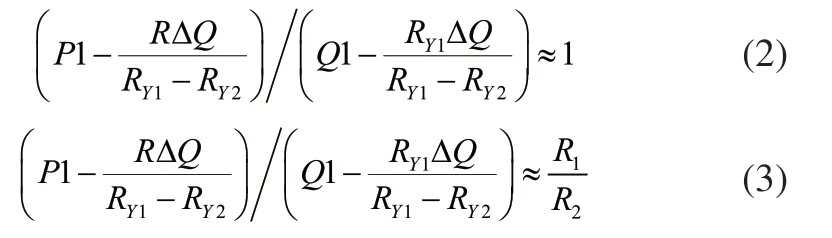
式中，P1、Q1分别指车轮X1、Y1的光耦输出脉冲数，ΔQ由式(1)求出，R、RY1、RY2分别为车轮X1、Y1、Y2与车轮X2之间的距离，R1、R2分别为车轮X1、Y1与车轴中点之间的距离。

由于运行状态复杂多变，判定式不能绝对相等。在时间Δt内，判定式(2)和式(3)成立，则在车轮打滑时，若扫地机器人运行方向向右偏转，则扫地机器人在直行和转弯状态，均不存在两个车轮都打滑的状态。

根据式(2)和式(3)，可列出在车轮打滑引起扫地机器人运行方向向左偏转状态，是否存在两个车轮都打滑的判定式。

3 方向误差计算与校正

扫地机器人运行时，在t1，t2，t3,…,tn时刻，根据式(1)计算车轮Y2与Y1的光耦输出脉冲数差值分别为ΔQ1，ΔQ2，ΔQ3，…，Δ Qn，扫地机器人运行的累计误差为：

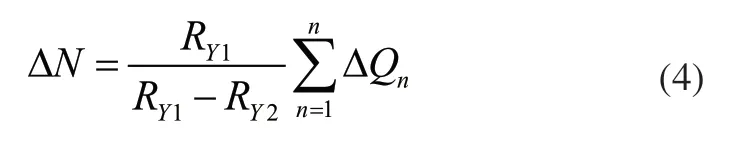
式中RY1、RY2分别为车轮Y1、Y2与X2之间的距离。双轮检测系统根据累计误差对误差进行修正，修正量为：

式中，R、RY1、RY2分别为车轮X1、Y1、Y2与车轮X2之间的距离，ΔN由式(4)计算得出。

误差校正阈值记为Nd。正向校正的方法为：若扫地机器人行驶的累计误差ΔN≥Nd，正向驱动左驱动轮X1，修正量为S；若累计误差ΔN≤(-Nd)，正向驱动右驱动轮X2，修正量为S。

反向校正的方法为：若扫地机器人行驶的累计误差ΔN≥Nd，反向驱动右驱动轮X2，修正量为S；若累计误差ΔN≤(-Nd)，反向驱动左驱动轮X1，修正量为S。

4 仿真验证

4.1 仿真参数

主要参数如下：车轮的半径r=3.5cm；电机减速输出n=1r/s；减速比i=30；测速片栅片数x=30；车轮X1与X2之间的距离R=40cm；车轮Y1与X2之间的距离RY1=30cm；车轮Y2与X2之间的距离RY2=10cm；采样周期ΔQt=0.2s；误差校正阈值Nd=8。

4.2 仿真结果与分析

仿真时，扫地机器人运行13.6s，每个采样周期采集到车轮的光耦输出脉冲数如图2所示，(a)、(b)、(c)、(d)分别为车轮X1、Y1、Y2、X2的光耦输出脉冲数。(a)与(d)中，正值表示车轮正向驱动，负值表示车轮反向驱动。

根据驱动轮轮X1、X2的光耦输出脉冲数，扫地机器人的预设行驶轨迹如图3所示。

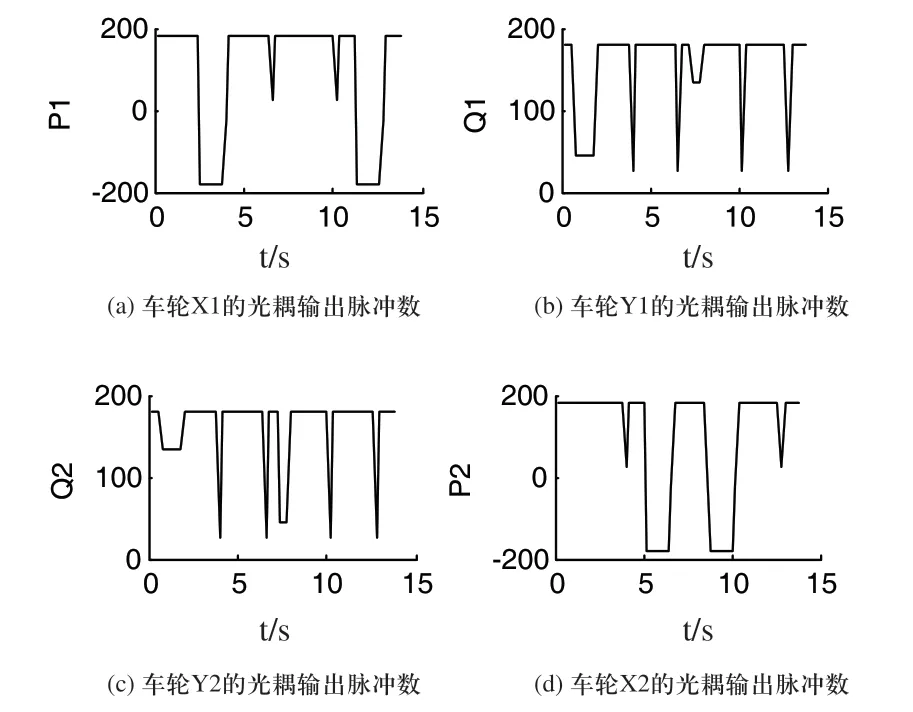
图2 车轮光耦输出脉冲数

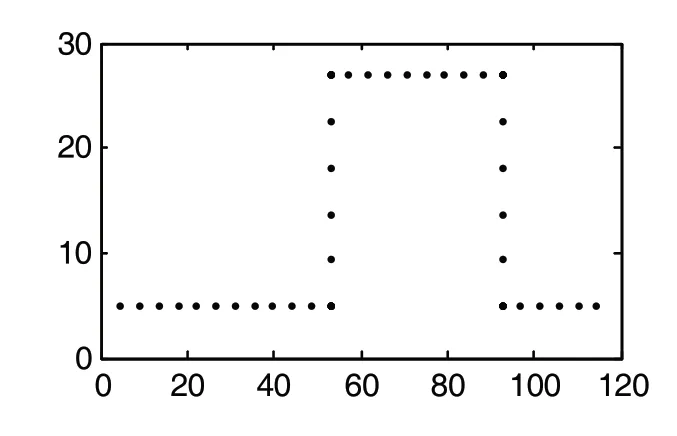
图3 预设行使轨迹

如果不对车轮打滑引起的运行方向误差进行修正，根据驱动轮X1、X2与检测轮Y1、Y2的光耦输出脉冲数，扫地机器人的未修正行驶轨迹如图4所示。

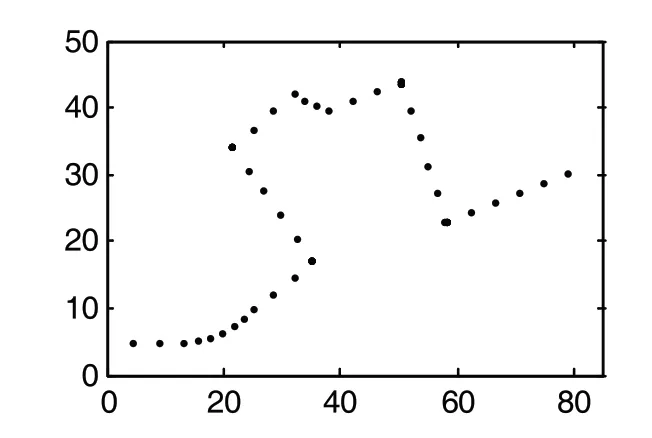
图4 未修正行驶轨迹

利用正向校正对车轮打滑引起的方向误差修正，修正后的行使轨迹如图5所示。可见，采用正向校正对行驶方向误差修正后，产生位移误差，但修正后扫地机器人行驶轨迹与预设行驶轨迹基本保持一致。经分析，位移误差方向与扫地机器人行驶方向垂直，若左驱动轮打滑，则存在左位移误差，若右驱动轮打滑，则存在右位移误差，位移误差大小与轴长R成正比例关系，位移误差大小为：

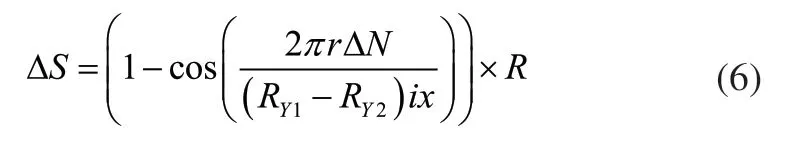
[1]刘维伟,张定华,史耀耀,等.航空发动机薄壁叶片精密数控加工技术研究[J].机械科学与技术,2004(03):329-331.

[2]Rai J K,Xirouchakis P.Finite element method based machining simulation environment for analyzing part errors induced during milling of thin-walled components[J].International Journal of Machine Tools and Manufacture.2008,48(6):629-643.

[3]Ratchev S,Liu S,Huang W,et al.An advanced FEA based force induced error compensation strategy in milling[J].International Journal of Machine Tools and Manufacture.2006,46(5):542-551.

[4]武凯,何宁,廖文和,等.薄壁腹板加工变形规律及其变形控制方案的研究[J].中国机械工程,2004(08):14-18.

[5]尹飞鸿,唐国兴,陈志伟,等.铝合金航空薄壁框铣削变形预测研究[J].制造业自动化,2012(18):34-36.

[6]周孝伦,张卫红,秦国华,等.基于遗传算法的夹具布局和夹紧力同步优化[J].机械科学与技术,2005(03):339-342.

[7]秦国华,吴竹溪,张卫红.薄壁件的装夹变形机理分析与控制技术[J].机械工程学报,2007(04):211-216.

[8]刘海涛.精密薄壁回转体零件加工残余应力及变形的研究[D].哈尔滨工业大学,2010.

[9]Li B,Melkote N.Improved workpiece location accuracy through fixture layout optimization[J].In ternational Journal of Machine Tools &Manufacture.1999(39):871-883.

[10]董辉跃,柯映林.铣削加工中薄壁件装夹方案优选的有限元模拟[J].浙江大学学报(工学版),2004(01):18-22.