基于有限元理论的轮轨接触力学特性仿真研究

郭伟杰，王旭东，刘邱祖

GUO Wei-jie, WANG Xu-dong, LIU Qiu-zu

（太原理工大学 机械工程学院，太原 030024）

0 引言

近年来，中国铁路运输业朝着高速重载的方向发展，对其传动部件的力学性能提出了更高的要求。

传统的Hertz[1]接触理论在计算轮轨接触压力时便于操作，简单易懂，但是该理论是在接触表面光滑，弹性变形等前提下推导的，而实际的轮轨接触过程中会有塑性变形，接触表面有摩擦，Hertz接触理论与实际工况相差较大Cater[2]。在Hertz接触理论的基础上，推导出轮轨接触的切向应力，但是轮轨接触问题是一种高度非线性行为，传统理论所得结果总会存在偏差。如今许多学者借助有限元理论来分析轮轨接触问题，张军[3]用有限元参数二次规划法，对多种工况进行弹塑性分析；陶功权[4]利用数值程序CONTACT和有限元模型进行了对比，说明有限元理论适用性更广泛；孙明昌[5]用有限元分析软件ANSYS对弹性轮对进行了应力、变形和模态计算分析。

本文借助有限元理论，分析两种轮径分别在不同轴重和不同横移量下的轮轨接触应力变化。

1 建立有限元模型

高速动车组车轮踏面选取LMa型，车轮宽度是135mm，轮径分别取Φ860mm，Φ920mm；钢轨选用CHN60。由于轮轨接触的对称型，在用Pro/E建模时只取左侧钢轨和左侧轮对的一半模型，这样可以减少网格单元，节省计算时间。钢轨长度取300mm，轨底坡为1:40，轨距为1435mm，轮对内侧距为1353mm。

有限元单元[6]采用Solid 45，在加载过程中，轮轨接触表面会发生塑性变形，假设轮对和钢轨的材料相同，弹性模量Ee=210GPa，泊松比γ=0.3；屈服极限σs=450MPa，应变强化模量Ep=21GPa，摩擦系数μ=0.2。网格划分及加载情况如图1所示，根据弹性力学理论[7]，接触区域附近的网格应该细化，网格尺寸取0.5mm～1mm[8]，远离接触区域，网格尺寸可以大些，这样不会影响计算精度，如图2所示，共产生98725个节点。

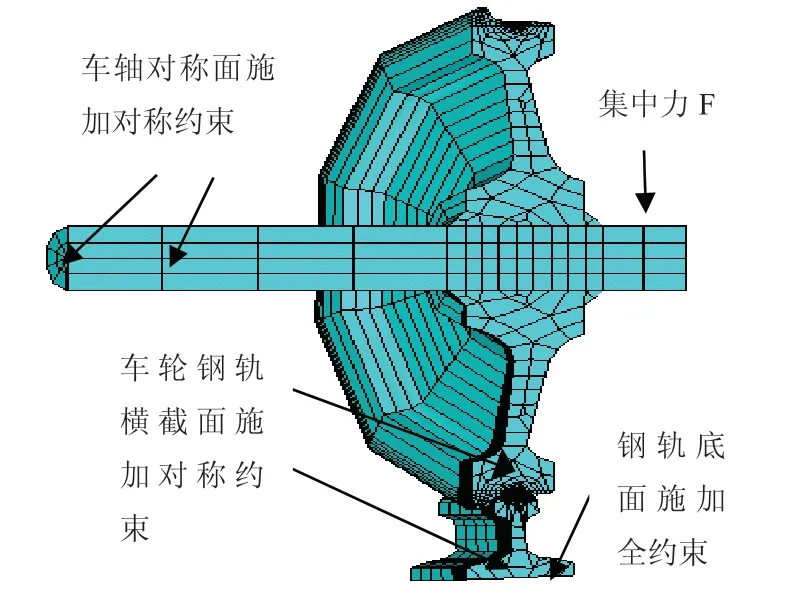
图1 轮轨接触有限元模型

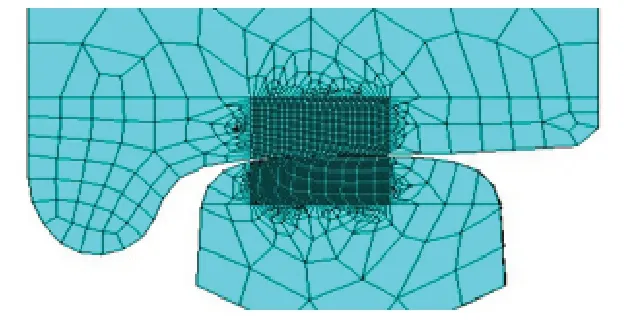
图2 轮轨接触区周围网格细分

2 结果分析

轮轨接触过程中接触斑的面积一般只有100mm2～200mm2，然而如此小的接触斑上却承受极大的外载，因此轮轨接触应力很大，这是造成车轮踏面磨损和疲劳的主要原因。本文主要考察轴重和横移量对接触应力的影响。

2.1 轴重对轮轨接触应力影响

参照动车组相关技术参数可知，每个轮对承受的载重约为10t～17t，为了分析轴重对接触应力的影响[9]，分别取11t、13t、15t、17t进行分析。

图3为轮轨间最大Mises应力随轴重的变化，图4为轮轨间最大垂向应力随轴重变化。由两图可知，随着轴重的增加，两种轮径的轮轨接触应力都在变大，并且Φ860mm车轮轮轨最大接触应力始终大于Φ920mm车轮的，这与Hertz接触理论有相同的变化趋势：

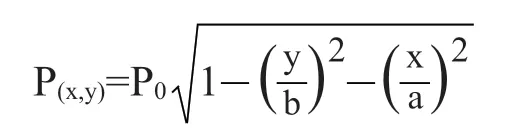
P(x,y)为接触班上任一点的压应力；

p0为轮轨接触斑上的最大压应力；

p为轮轨间的垂向力；

a,b为椭圆接触斑的长半轴，短半轴。

所以轮径在一定程度上可以改善轮轨受力状态，车轮运营一段时间后，由于疲劳磨耗等原因需要进场返修，进行旋削处理后，车轮半径会变小，会恶化机车的运行品质。

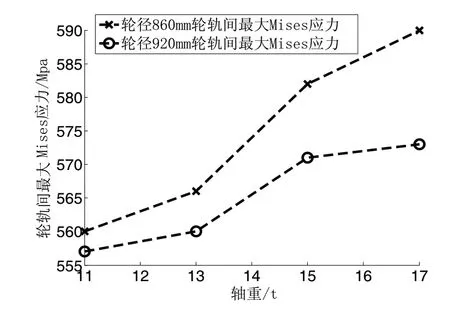
图3 轮轨间最大Mises应力随轴重的变化

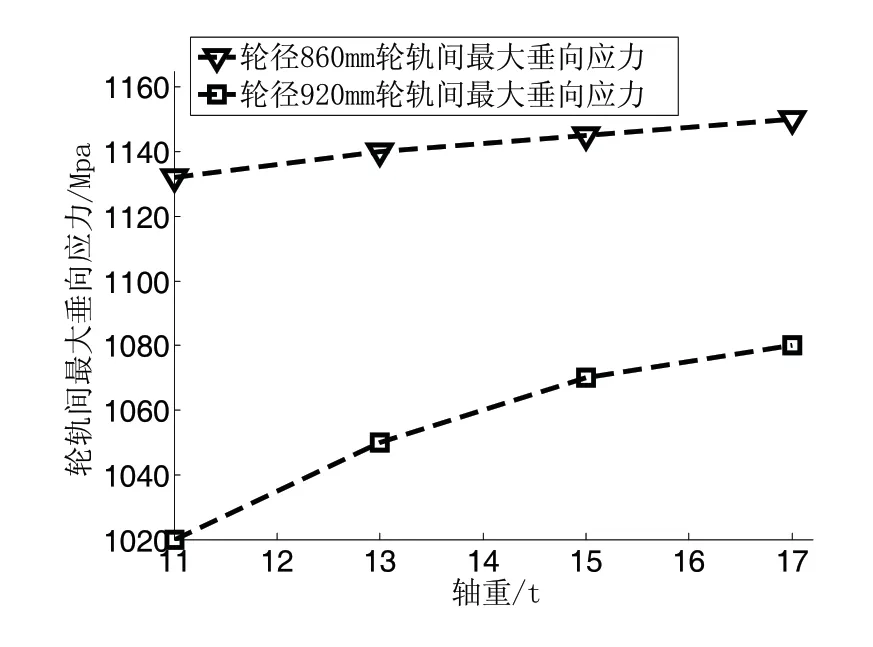
图4 轮轨间最大垂向应力随轴重变化

图5显示了轮轨接触斑面积随轴重变化趋势，由图可知，随着轴重的增加，两种轮径的轮轨接触斑面积都在变大，Φ920mm车轮轮轨接触斑面积增加了38%，Φ860mm车轮的接触斑面积增加了5.6%，Φ920mm车轮轮轨接触斑面积大于Φ860mm车轮的，所以Φ920mm车轮的轮轨接触应力小于Φ860mm车轮的。

以17t轴重为例，图6中(a)、(b)分别为沿横向截面观测，根据材料力学第四强度理论主要考察轮径Φ860mm，Φ920mm的轮轨接触等效Mises应力云图。从两图中可知，车轮上最大等效Mises应力距接触面约2mm～4mm，这一区域正是产生微裂纹的危险区域，车轮上沿图中箭头方向接触等效Mises应力先变大再变小，因此在加工制造车轮过程中，要合理分配轮辋内部的硬度。

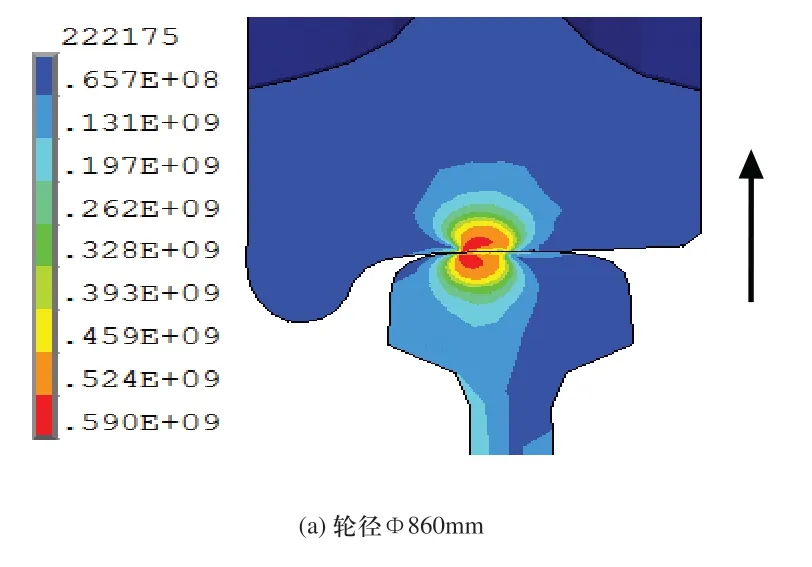
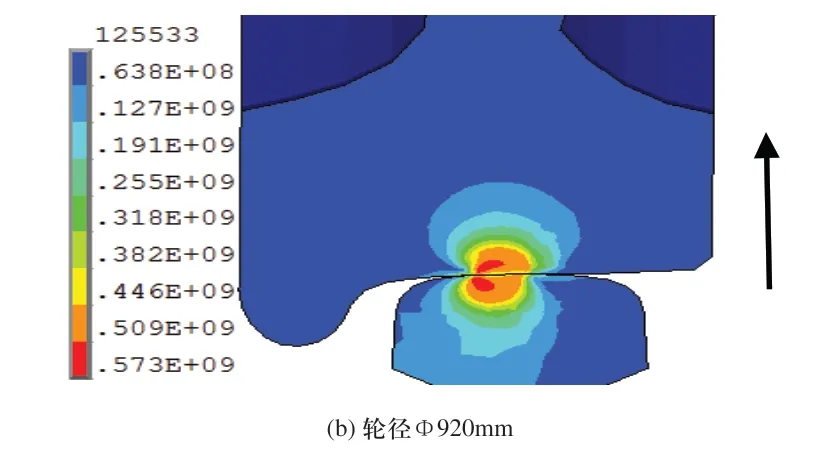
图6 轴重17t下轮轨接触应力

2.2 横移量对轮轨接触应力影响

由于磨耗型车轮踏面和钢轨顶面都是由多段圆弧连接而成的，理想状态下车轮与钢轨应该对中接触，但由于列车线路的复杂性（如高低不平顺，垂向不平顺等）使得轮对的对称平面和钢轨的对称平面总有一个横移量，如图7所示：y就是横移量。已有研究表明较大的横移量会导致轮缘和钢轨接触，使得轮轨间形成两点接触，加剧轮缘磨耗。本文考察横移量由-3mm～3mm的轮轨接触应力变化，横移量为正值表示钢轨靠近轮缘侧，负值表示钢轨远离轮缘侧。

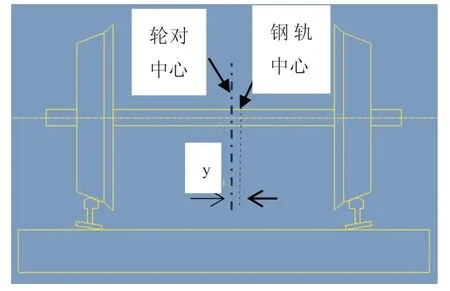
图7 有横移量的轮轨接触示意图

图8显示了轮轨间最大Mises应力随横移量变化，从图中可知两种轮径的最大Mises应力都经历了先变大后变小的过程，轮轨间最大Mises应力都出现在对中接触的位置，这时左右轮轨受力状态相同，有利于两侧车轮的均匀磨耗。任何一种轮径靠近轮缘侧的轮轨间最大Mises应力大于远离轮缘侧，这是因为靠近轮缘侧车轮踏面接触面上曲率半径变化较大，会直接影响轮轨接触斑面积。这种情况常见于列车过曲线时，左右车轮不同的受力情况会造成不均匀磨耗。Φ860mm轮径的最大Mise应力始终大于Φ920mm轮径的，说明在有横移的情况下，不同的轮径受力状态不同。

图9显示了轮轨间最大垂向应力随横移量变化趋势，从图中可知轮轨对中接触时轮轨间最大垂向应力达到最大值，这是因为对中接触时，左右车轮瞬时滚动圆直径差为零，轮轨间无横向分力，垂向力全部由轴重来提供。Φ860mm轮径的最大垂向应力始终大于Φ920mm轮径的。对于Φ920mm车轮远离轮缘侧的轮轨间最大垂向应力大于靠近轮缘侧的，而Φ860mm左右两侧车轮的最大垂向应力无明显变化，这是因为Φ860mm车轮轮轨接触斑面积在不同横移量下的变化较小造成的。

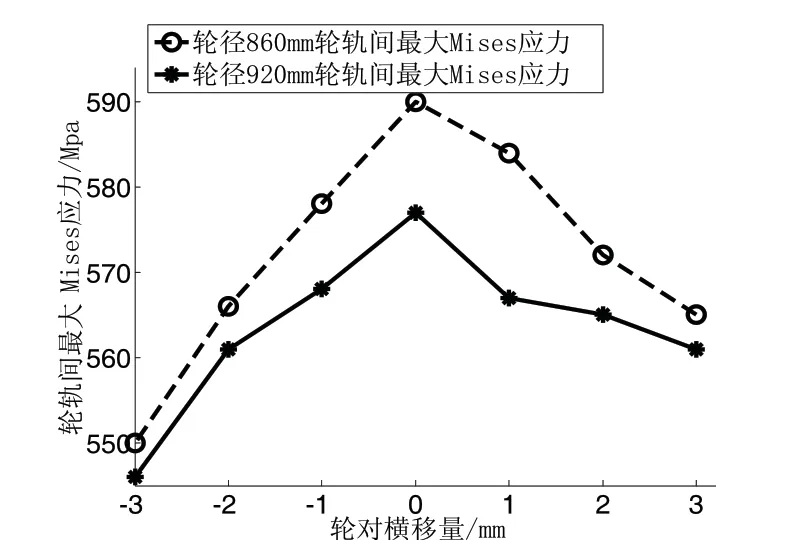
图8 轮轨间最大Mises应力随横移量变化

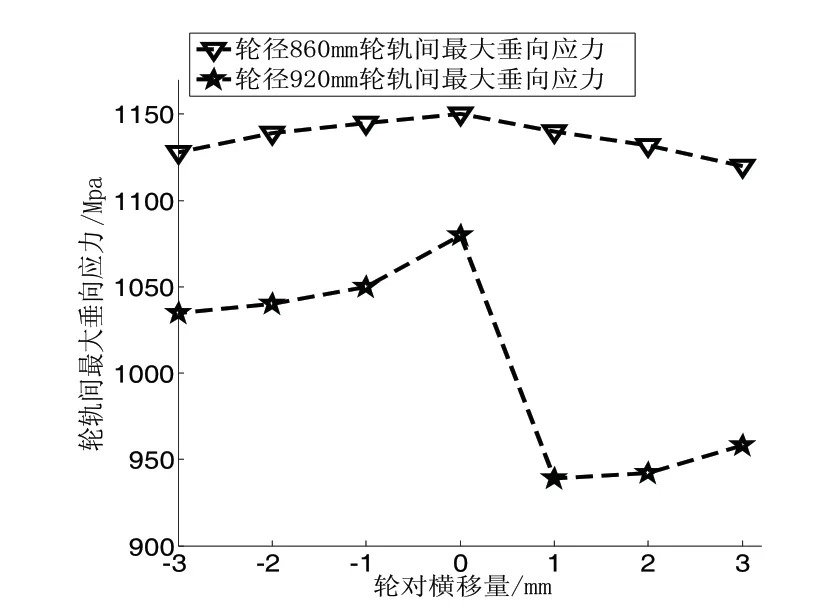
图9 轮轨间最大垂向应力随横移量变化

图10显示了轮轨间最大剪切应力随横移量变化趋势，从图中可以看出不同横移量下，轮径为Φ860mm的剪切应力变化比较大，并且两种轮径下的剪切应力变化趋势较相似，轮轨对中接触时，剪切应力是最小的，这是因为在无横移量时，左右轮轨几何接触角相等，横向力可以抵消，因此可以认为横向力会影响剪切应力的分布。

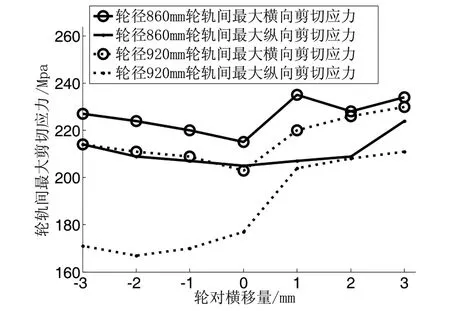
图10 轮轨间最大剪切应力随横移量变化

考察17t轴重下，不同横移量的轮轨接触应力分布情况。图11(a)、(b)分别为沿横向截面观测，偏移量L=3mm，Φ860mm，Φ920mm的轮轨接触等效Mises应力云图。从两图中可知，车轮上最大等效Mises应力在车轮踏面上，车轮上沿箭头方向接触等效Mises应力不断变小，两种轮径在改横移量下的等效应力差别较小。

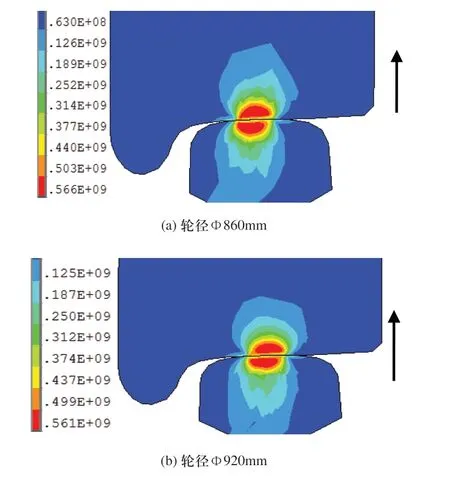
图11 偏移量L=3mm，轮轨接触应力

3 结论

1）有限元分析中考虑了材料的弹塑性变形，Hertz接触理论是在小变形和弹性半空间的前提下推导的，但是增加轴重时，两种轮径的受力状态有相同的变化趋势，都在缓慢增加，并且Φ920mm车轮的接触应力小于Φ860mm车轮，说明车轮轮径对轮轨接触状态有一定影响。

2）轮轨对中接触时，接触应力最大，左右两轮受力状态相同。当车轮有横移量时，发现靠近轮缘侧车轮的接触应力大于远离轮缘侧的车轮，这时左右两车轮受力状态不相同，容易造成偏磨，不利于车轮合理的使用。

3）车轮有横移量时，Φ920mm车轮的接触应力小于Φ860mm车轮，两种轮径在车轮有横移量时，垂向应力变化不明显，而切向应力变化较大，说明轮轨间的切向应力主要受横移量的影响。

[1]Hertz,H.über die berührung fester elasticher kürper[J].Journal für und angewandte Mathematik,1882,92:156-173.

[2]Carter F W.On the action of a locomotive drivingwheel[J].Pro.R.Soc.,London,A.1926,112:151-157.

[3]张军.轮轨接触问题的弹塑性分析[J].铁道学报,2000,22(3):17-21.

[4]陶功权.两种轮轨接触应力算法对比分析[J].工程力学,2013,30(8):229-235.

[5]孙明昌.弹性轮对的有限元分析[J].交通运输工程学报,2002,2(4):39-42.

[6]曾攀.有限元基础教程[M].北京,高等教育出版社,2009.

[7]徐芝纶.弹性力学简明教程[M].北京:高等教育出版社,2002.

[8]卢勇.大功率机车轮轨接触问题研究[D].南昌:华东交通大学,2010.

[9]曹明,宋春明,张东生.基于ANSYS的定梁龙门机床横梁静力学特性分析[J].制造业自动化,2015,37(03):87-89.