基于舟山外海连续测站的湍混合研究*

史军强，陈学恩

（中国海洋大学海洋环境学院，山东 青岛 266100）

湍流是海洋中普遍存在的一种高度无序的、随机的、非线性的高频流动，被认为是经典物理中最后一个未被解决的难题。湍流混合在对海洋能量和水体的交换的转变过程中起着至关重要的作用，它可以引起海洋动量、热量、物质在水平和铅直方向的传输，使海水的各种性质趋向均匀，是海洋中众多物理、生化过程的核心。它的影响不仅仅限于海洋本身，研究发现，湍流混合同样对全球气候系统的维持与变化有着重要影响［1］。海洋的内部混合已经成为制约海洋科学、大气科学等相关领域研究的关键和瓶颈。因此，对海洋湍混合的研究也自然成为了当前物理海洋学诸多研究中的意义重大的热点问题。

陆架海是全球海洋动力过程最为活跃的部分。Egbert和Ray指出，全球潮能耗散的60%～70%发生在陆架海［2］。同时，陆架海也是与人类生存和发展最为密切相关的海域，占全球海洋总面积8%的陆架海是海洋初级生产力最为密集的区域，贡献了全球初级生产力的15%～30%，全球90%的渔业资源均来自于陆架海。此外，陆架海也是人类从事航运、石油钻探开采等生产活动的重要场所。因此，开展陆架海的湍混合研究无论在学术领域还是在经济领域都有着重要的意义和价值。

虽然混合的观测与研究已得到广泛的开展，但是，中国近海由于观测资料有限，湍混合研究仍然较为少见。钟贻森等利用夏冬两季黄东海水文与微结构观测资料，分析了黄、东海域湍流混合与双扩散现象的空间分布特征与季节变化，指出黄东海陆架湍流混合除了与风应力、底摩擦等外界强迫条件有关外还与局地环流和水团有密切联系［3］。刘志宇从观测资料出发，给出了黄海湍流混合变化特征，通过计算表明，黄海底边界层存在很强的湍耗散并且具有明显的周期变化规律［4］。在南海海域，卢著敏等利用LADCP与CTD资料对南海中深层混合进行估计，对由垂向翻转引起的混合进行分析，结果表明，研究海域中深层存在较频繁的垂向翻转，翻转所对应的混合率并不随深度的增加而减少［5］。上述成果加深了人们对中国近海湍混合特征的了解和认识。

为了研究潮流占优的陆架浅海区冬春转换季节的湍混合特征，本文利用2010年4月3日舟山外海A站（29.599°N，123.211°E）进行的一次周日（25h）定点连续观测数据，计算了Thorpe位移、Thorpe尺度、湍动能耗散率、湍混合率等混合参数并探讨了其显著周期及时空变化规律，定量地揭示了该季节舟山外海的湍混合特征。

1 观测与数据介绍

中国海洋大学“东方红2”科学考察船于2010年4月1日～6日在杭州湾外的舟山海域进行了为期6d的海洋综合调查，并于4月3日7时～4日7时（北京时）在A站点（水深68m）（见图1）进行了连续25h的流速、温度、盐度、密度及压力等要素的观测。已有的水文分析和短期的测流结果表明，台湾暖流在东海西部陆架终年存在并且沿50～100m等深线向北流动［6］。由于A站点所处位置正处于台湾暖流核心流域范围内，海况复杂，同时A站点位于中国最大渔场——舟山渔场的范围之内，因此，对该站点湍混合的研究具有重要性、典型性和代表性。A站点流速采用频率为300kHz的LADCP进行观测，其发射角为20°，共有4个发射波束，单次测量40层，每层的厚度为2m。每小时观测一次。由于LADCP的探测信号能够到达海底，因此可以根据每一层相对于海底的底跟踪流速以剪切法分别求取每一层的流速。原始观测的数据为二进制格式，以BBLIST软件进行格式转换并设置输出形式。对所得数据进行质量控制：

（1）设定U、V、U-error、V-error＜99.99，剔除无资料的观测；

（2）设定percentage＞85，去掉品质不好的观测；

（3）设定U、V的绝对值小于1.5m/s，误差绝对值小于0.5m/s。

经过上述的质量控制，对每2m层厚度内的数据取平均，得到的最终海流数据用于本文的分析。

A站点的温度、盐度、密度、压力数据使用美国Seabird公司生产的CTD温盐深仪进行测量。使用仪器自带的SBEDataPocessingWin32软件对原始数据进行处理［7］，处理步骤包括：工程量转换、滞后订正、热通量订正、异常值剔除、低通滤波、消除逆压、平均处理。最终，得到时间分辨率为1h，垂向分辨率为1m的温度、盐度、密度、压力数据。

观测期间的A站点的水位数据（相对于平均海面）及10m风场数据如图2所示。其中水位与风场数据的采样时间均为1h。

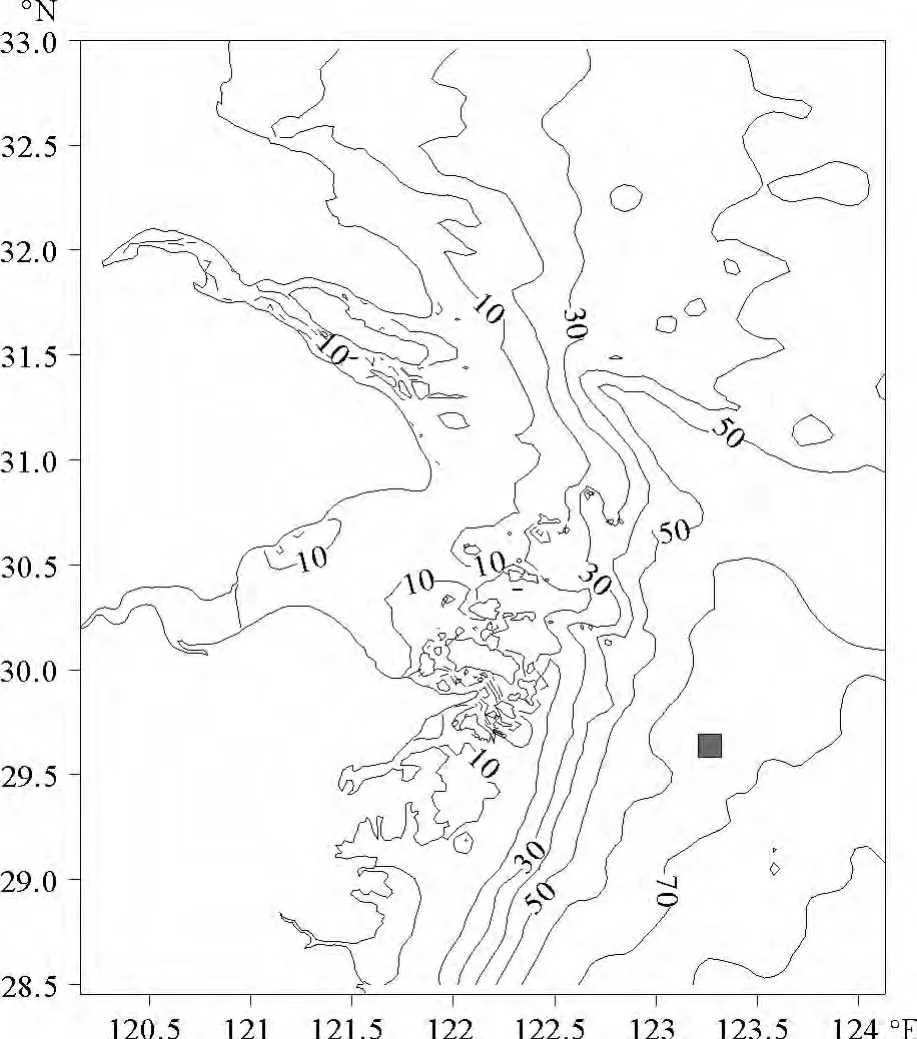
图1 观测点位置（■A）及地形Fig.1 Observation station（■A）and topography

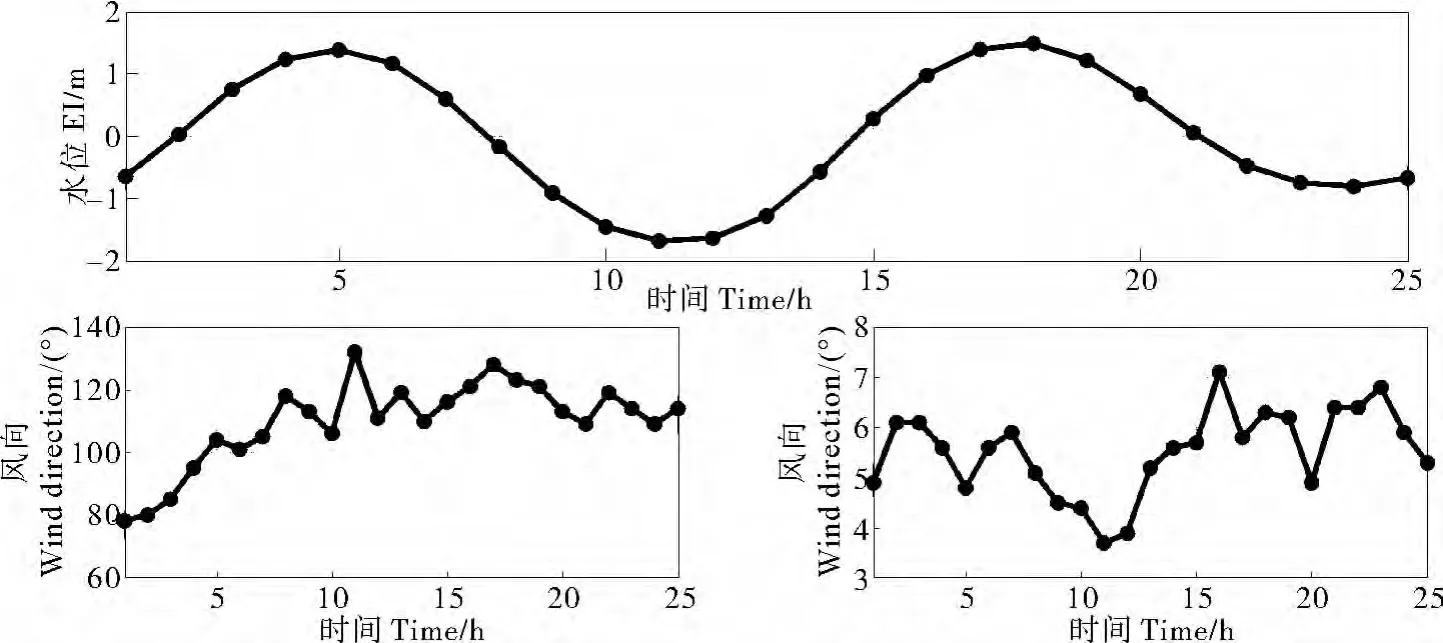
图2 观测期间A站点处的水位序列（上）、风向（下左）及风速（下右）序列Fig.2 Time series of water elevation，wind direction and wind speed at A station

可以看出，在观测期间水位最大值为1.67m，共出现了2次高潮和2次低潮。相邻2个波峰/波谷的时间间隔约为12.5h，表现出明显的正规半日潮特征。风向在前3h为西南风，其余时间均为西北风。最小风速为3.7m/s，最大为7.1m/s。

2 数据分析和讨论

2.1 湍流垂向翻转

在层结湍流中，Thorpe尺度LT通常用来表征湍流所致的垂向翻转［8］。通常所知，在层结稳定的水体中，位密度剖面的结构必定是从海面的最小值由小到大排列至海底，如果有发生位密度翻转的情形即密度较大的值对应的深度比密度较小值对应的深度浅或反之，则可视为湍流扰动的结果。本文采用Thorpe提出的算法来估计LT［9］。先将观测到的位密度剖面重新排列得到分层稳定的剖面，则位密度的原位置与重排之后的位置之间的距离称为Thorpe位移，通常位移是一段一段地分布在剖面上，每一段的前后皆为零，本文将每一段称为一个位密度翻转事件。LT则被定义为每一段Thorpe位移的均方根。以第15小时的观测数据为例，计算过程如图3所示。

其中，图3（a）是重排前后位密度的剖面对比图，由于图例比例的原因，图中位密度剖面重排前后的差别不明显。图3（b）则是将图3（a）在56～66m的深度范围上进行了放大，可以看到，图中同一深度处都对应着的不同的位密度，这就是密度的波动。图3（c）即是由密度波动得到的Thorpe位移。图3（d）则是根据Thorpe位移计算得到的Thorpe尺度的垂向分布。需要说明的是，在Thorpe位移与Thorpe尺度的垂向分布图中有很多零值点，这并不是说在这些点对应的深度上不存在湍流翻转，而是受分辨率限制，无法分辨小于1m的翻转。图4（a）为Thorpe尺度的时空分布图以及水位的时间序列。

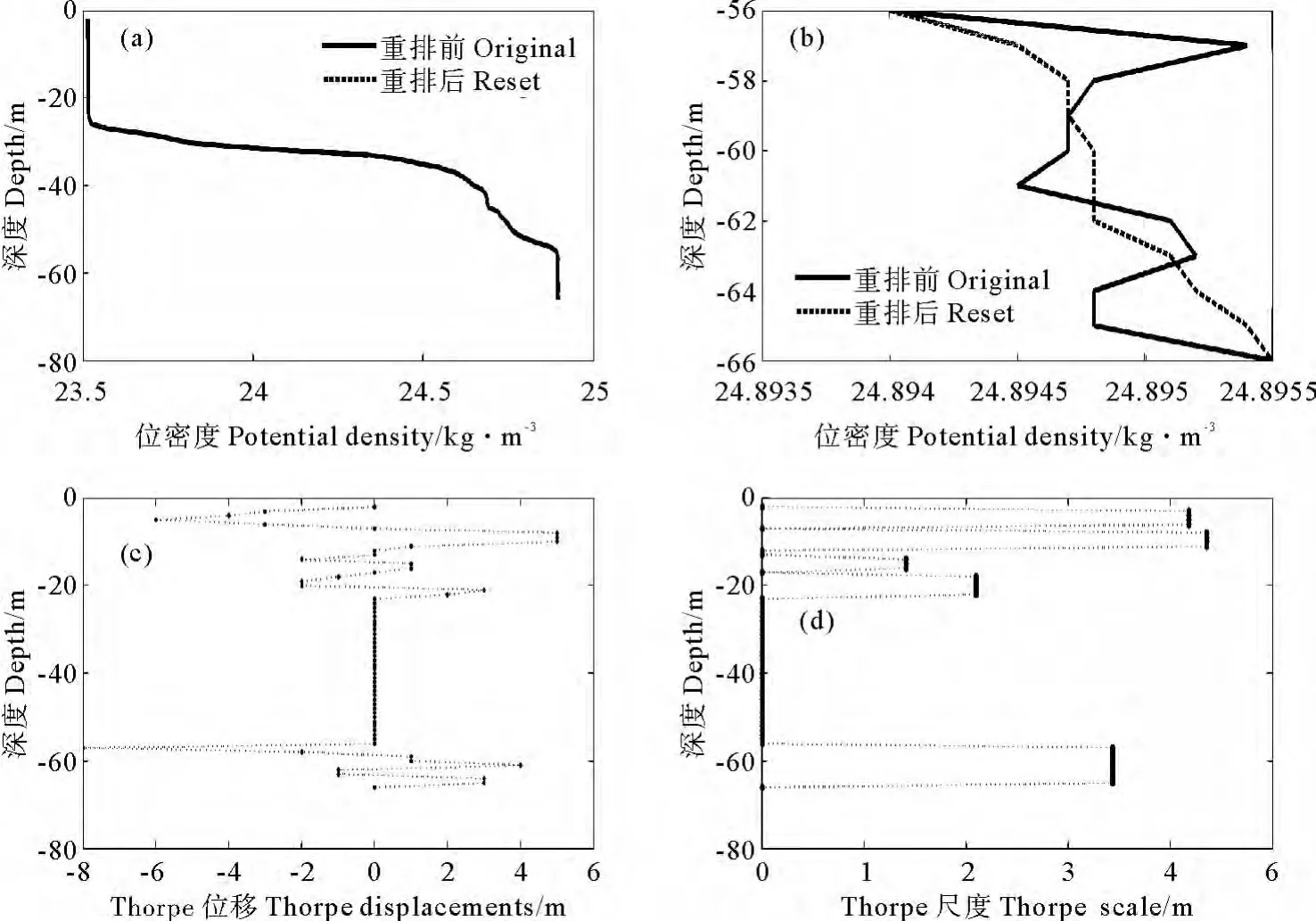
图3 Thorpe算法示意图Fig.3 Schematic diagram of Thorpe method

结果显示，Thorpe尺度在垂向上呈现出明显的分层，上层最大，下层次之中层最小，最大值可以达到11.17m且Thorpe尺度的大值均出现在水位序列的峰值附近。对Thorpe尺度做垂向平均并对其垂向平均时间序列（见图4（b））进行功率谱分析（见图4（c））表明，垂向平均的Thorpe尺度具有显著的半日周期、1/4日周期及2.4h的周期，其中半日周期最为显著。上述分析说明，湍流翻转与潮汐关系密切。按照涨潮落潮时间分别计算整层的Thorpe尺度发现，涨潮时段内平均Thorpe尺度为3.44m，而落潮时段内的平均Thorpe尺度仅有2.1m，涨潮的湍流翻转明显大于落潮时的湍流翻转。

2.2 Brunt-Vaisala频率

在对湍耗散与湍混合进行评估之前首先要计算Brunt-Vaisala频率。Brunt-Vaisala频率是指在层结稳定的海洋中，海水微团受到某种力的干扰后，在铅直方向自由振荡的频率［10］。它主要决定于海水密度的铅直梯度dρ/dZ，近似计算公式为：

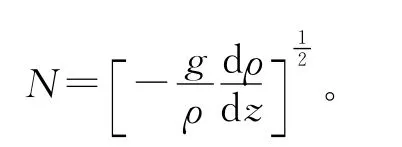
因此，本文可以根据前文得到的重新排列后的密度剖面来计算Brunt-Vaisala频率。图5即为计算得到的Brunt-Vaisala频率垂向分布随时间的变化。

图中可以看出，Brunt-Vaisala频率的大值部分呈现出两条明显的带状分布，一条在15～35m深度范围内波动，另一条在40～55m深度范围内波动，且上层带状内Brunt-Vaisala频率的强度要明显大于下层带状内的强度。经计算可得，上、下两带状区域观测时间内平均的密度垂直梯度分别为0.197和0.04kg/m4，均在《海洋调查规范》所规定的强弱密度跃层临界值之上［11］，这表明该站点在观测期间铅直方向上呈现出了显著的双密度跃层结构。为方便下文分析，本文将两密度跃层中Brunt-Vaisala频率最大值所在位置称为密度跃层核心深度。求取每个观测时刻两密度跃层中Brunt-Vaisala频率最大值所在位置，即可得到图6（a）所示的两密度跃层核心深度的时间序列。可以看到两核心深度随时间均出现不同程度的的起伏，表现出明显的湍扰动特征。为此，分别对这2个时间序列进行功率谱分析，结果分别绘于图6（b）（强跃层）、图6（c）（弱跃层）。结果显示，强密度跃层核心深度序列的显著谱峰主要集中在周期为3～5h、9～17h的范围内，其中在4.4和11h周期处存在最显著的谱峰，这说明在强密度跃层中表现出了明显的高频内波和近半日潮频率的内潮特征。弱密度跃层核心深度序列的显著谱峰主要集中在周期为5～22h的范围内，其中在22h周期处谱峰最为显著，其次是11h周期处。可见，与强密度跃层有所不同，弱密度跃层中则是近惯性频率的内波和近半日潮频率的内潮特征明显。汪嘉宁和魏皓等也曾通过对东海陆架一连续测站的春季水文环境的日变化特征分析得到过类似的结论［12］。

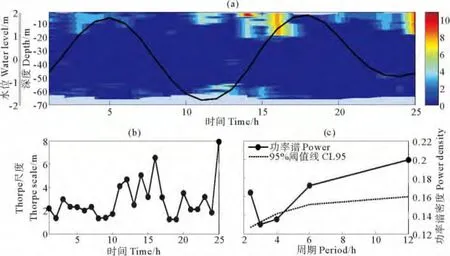
图4 Thorpe尺度时空分布及水位时间序列（图中黑线）（a），Thorpe尺度垂向平均时间序列（b），对Thorpe尺度垂向平均时间序列的功率谱分析（虚线为95%信度水平阈值线）（c）Fig.4 Distribution of Thorpe scale and time series of water elevation（a），vertical averaged Thorpe scale（b）and spectrum analysis for vertical averaged Thorpe scale（c）

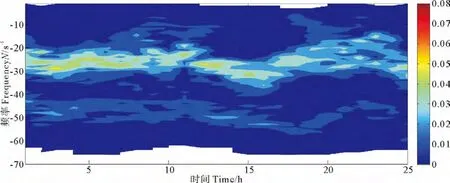
图5 Brunt-Vaisala频率时空分布Fig.5 Temporal and spatial distribution of Brunt-Vaisala frequency

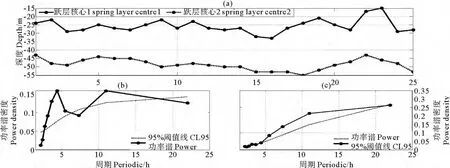
图6 密度跃层核心深度（a）及其谱分析结果（b，c）Fig.6 Distribution of spring layer center（a）and spectrum analysis（b，c）

2.3 湍耗散与湍混合

根据上文估算出的Thorpe尺度LT和Brunt－Vaisala频率N，依据Dillon和Osborn［13］提出的公式

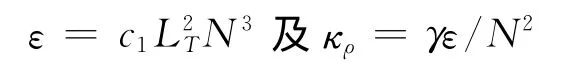
来估算湍动能耗散率ε和湍混合率κρ，其中：c1为经验常数，一般取为0.64；γ为混合系数，一般取为0.2。图7为计算所得深度平均的湍动能耗散率ε和湍混合率κρ的时间序列。

湍动能耗散率与湍混合率的时空分布分别如图8（a）、（b）所示。图中黑色曲线为上文所得到的强、弱密度跃层的核心深度曲线。在观测数据覆盖的25h，即一个周日的观测期间，该区域的湍动能耗散率平均为2.79×10－7W/kg，量级在10－10～10－6W/kg之间变化。湍混合率平均值为7.1×1 0－4m2/s，量级在10－5～10－2m2/s之间变动。

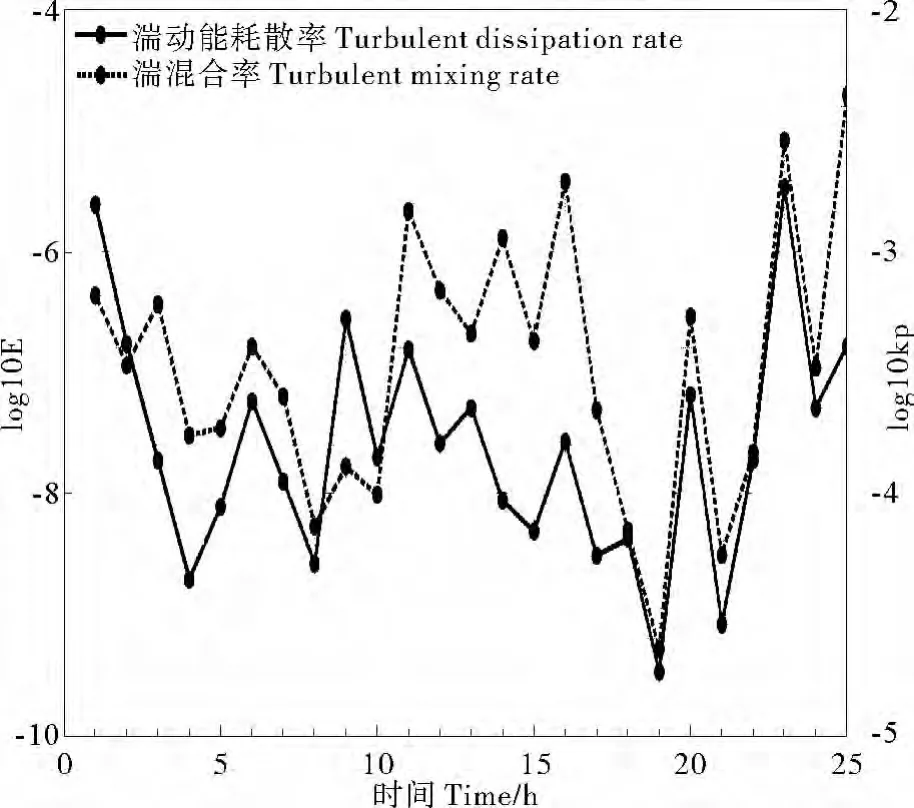
图7 深度平均的ε与κρ时间序列Fig.7 Time series ofεandκρ

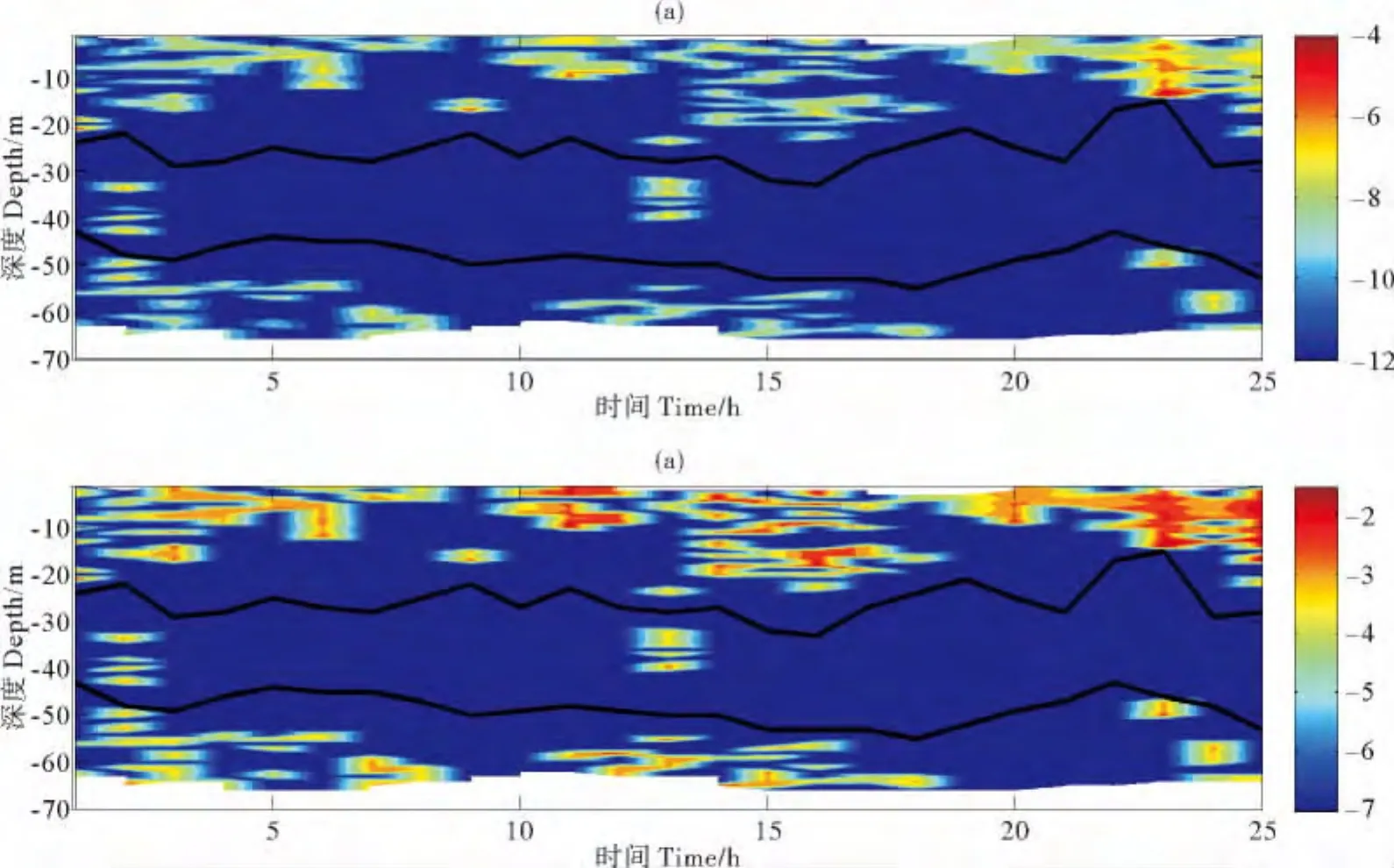
图8 湍动能耗散率（取对数，W/kg）时空分布（a）与混合率（取对数，m2/s）时空分布（b）Fig.8 Temporal and spatial distribution of turbulent dissipation rateε（a）and turbulent mixing rateκρ （b）（in log unit）

图中湍动能耗散率与湍混合率的时空分布基本一致，均以密度跃层核心深度曲线为界呈现出明显的上、中、下3层结构。无论是湍动能耗散率还是湍混合率，其强度均是在上层最大，下层次之中层最小，这从物理上也容易理解，中层上下均以密度跃层的核心深度为界，层结最强，水体最稳定，因而对湍的抑制作用也最强烈，穿越等密度面的小尺度过程要克服层结的抑制作用需要更多的能量；上层水体极易受到海表面风应力等多种动力因素的影响；下层水体由于以海底为下边界显然要受到底应力作用的影响。而上跃层层结更强，穿越等密度面的小尺度过程要克服层结的抑制作用需要更多的能量。此外，从图中还可以看出，中层水体湍动能耗散率与湍混合率强度在观测的大多数时刻均接近于零，但是在个别时刻存在着间歇性的强混合现象。与跃层的限制作用相反，内波混合可以为环境要素跨跃层交换提供能量，而跃层的存在又为内波的产生提供了条件。本文在前面已证实，在中层水体上下边界内波活动活跃，尤其以高频内波、近半日潮频率的内潮和近惯性频率的内波信号最为显著。已有的研究表明，在层化季节，内潮、近惯性内波以及高频内波的剪切不稳定可以在水体内部造成间歇性的强混合，内波可能是促进该层水体湍混合的一个重要因素，但是对于造成间歇性强混合的机制至今尚不清楚。

2.4 湍混合特征及其影响因子

由于湍动能耗散率的时空分布特征与湍混合率基本一致，因此，本文只对湍混合率进行分析，并着重揭示研究海域上层和下层水体中的湍混合特征及其影响因子。

上层深度内，湍动能耗散率与湍混合率强度随深度变小，这主要是因为在上层，随着深度的增大，风应力、波浪破碎等外部作用的影响逐渐变小，另外，水体本身由于密度梯度逐渐变大而趋向稳定。为进一步揭示上层水体湍混合影响因子，本文对该层湍混合率进行垂向平均，分别与同步观测得到的海表风应力数据、相同深度平均得到的海流数据进行交叉谱分析来探讨它们之间的关联程度。由于涉及不同量纲，因此在分析之前本文对各要素序列进行了无量纲化处理［14］。

图9（a）是风应力与湍混合率的交叉谱分析［15］结果，图中水平虚线表示95%的置信度，结果显示，仅有周期为2.18h的振荡是显著的，其对应的落后长度谱值是－0.26，也就是说湍混合要滞后于风应力大约0.26h。海流流速与湍混合率的交叉谱分析结果（见图9（b））揭示了2个显著的振荡周期，1个位于4h处，另1个位于3.4h处，相关系数在4h周期处取得最大值为0.849，对应的落后长度谱值为－0.88，即湍混合要滞后于流速大约0.88h。综合以上结果，本文认为在观测时段内该站点的湍混合对风应力的响应要比对流速的响应迅速。由于掌握的数据有限，本文暂不讨论其它要素对湍混合的影响。

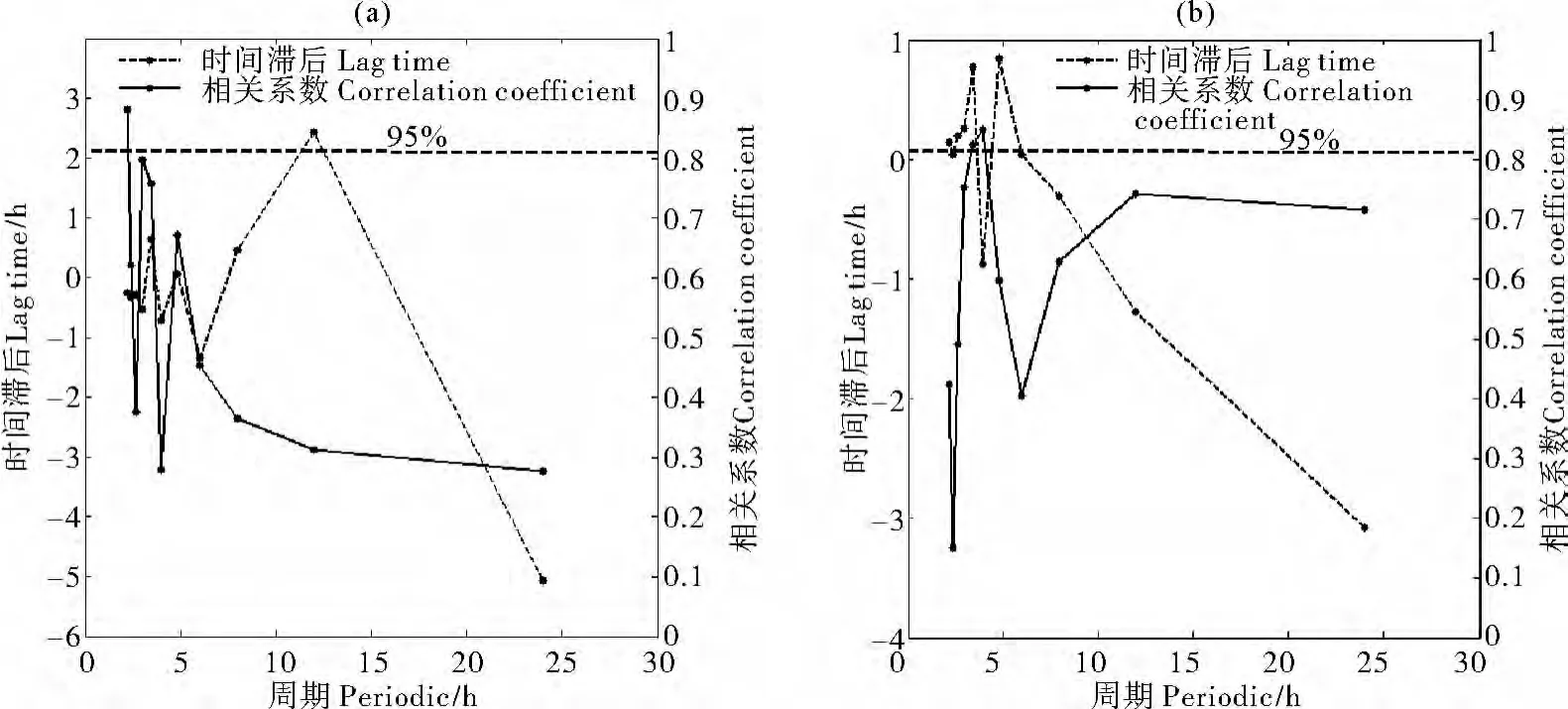
图9 风应力与湍混合率的交叉谱分析结果（a）及流速与湍混合率的交叉谱分析结果（b）Fig.9 Crossspectrum between wind andκρ （a）and Crossspectrum between current andκρ （b）

图8显示的A站点下层湍耗散系数与湍混合率的分布则表明，在下层水体湍动能耗散率与湍混合率强度随距海底高度的增加而减弱。这主要是因为随着离底高度的增加，底摩擦对湍混合的促进作用越来越不明显，同时水体也会由于密度梯度逐渐变大而趋向稳定。显然，底应力是下层水体湍混合不可忽略的影响因子。下面本文将根据LADCP测流数据来估计底应力并分析底应力与湍混合的关联程度。海洋边界层的结构和大气边界层有很多类似的地方，例如，普遍认为海洋边界层是一个对数层，即其流速随着离海底高度的增加而呈对数规律增加。该对数层位于地球旋转效应起主要作用的深度之下，同时又位于一个很薄的底边界层之上。在对数层内，流速剖面可以用如下公式表示［16］：

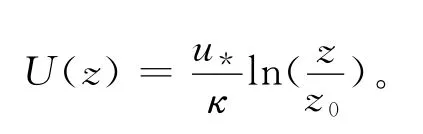
其中：U是平均流；z是距离海底高度；κ是VonKarman常数；z0为底粗糙度；u＊为摩擦速度。确定对数层的存在非常重要，因为它提供了一种估算底应力的方法。首先根据LADCP实测流速剖面和上述对数关系式，通过流速剖面对数拟合求取z0和u＊，然后根据公式：τ＝求取底应力τ，其中：ρ为海水密度。根据以上方法，本文得出了观测期间17个时刻的底应力的时间序列。由于在观测的第4～6小时、第9小时和第22～25小时速度剖面没有表现出明显的对数曲线特征，因此，为了不引进新的误差，本文将这8个观测时刻的数据舍弃，只对其他17个时刻进行对数拟合。将底应力时间序列与该层湍混合率进行垂向平均后的时间序列无量纲化后进行比较，结果如图10所示。从图中可以明显看出，湍混合率变化与底应力变化基本对应，底应力较大的时刻湍混合率也较大，混合较强。经统计，底应力与湍混合率的时间序列相关系数达到了0.602 1，这说明了底应力确实对该层水体的湍混合起到了重要作用。由于该站点所处位置地形复杂，可以推测，越接近海底，Thorpe尺度、湍混合率均会增加，不过这有待更深入的调查、更详尽的资料予以分析证实。

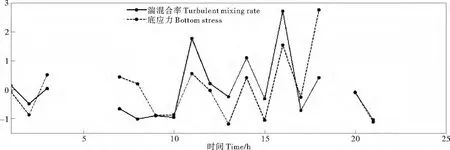
图10 湍混合率kρ与底应力τ的时间序列Fig.10 Timeseries of kρandτ

3 结论

本文基于舟山外海一个观测站位（A站）周日的LADCP、CTD资料，对该站位小尺度湍混合参数进行估计，分析并讨论了其时空分布特征及影响因子，得到如下结论：

（1）Thorpe尺度在垂向上呈现出明显的分层结构，最大值可以达到11.17m。Thorpe尺度的大值均出现于水位序列的峰值附近且涨潮时的湍流翻转明显大于落潮时的湍流翻转。功率谱分析表明，垂向平均的Thorpe尺度的半日潮周期最为显著。

（2）对Brunt-Vaisala频率的分析表明，观测期间该站点在铅直方向上呈现出了显著的双密度跃层结构。弱跃层中近惯性频率的内波和近半日潮频率的内潮信号最为明显而强跃层中则表现出了明显的高频内波和近半日潮频率的内潮特征。

（3）观测期间，湍动能耗散率的平均值为2.79×10－7W/kg，量级在10－10～10－6W/kg之间变化。湍混合率的平均值为7.1×10－4m2/s，量级在10－5～10－2m2/s之间变动。

（4）湍动能耗散率与湍混合率的时空分布基本一致，均以密度跃层核心深度曲线为界呈现出明显的上、中、下3层结构。中层水体层结最稳定，但伴有间歇性的强混合过程。下层水体湍动能耗散率与湍混合率强度则随离底高度的增加而减弱，底应力对该层水体的湍混合起到了重要作用。

（5）上层水体，湍动能耗散率与湍混合率强度随深度变小。交叉谱分析结果显示，湍混合率要滞后于风应力大约0.26h，滞后于流速大约0.88h，在观测时段内该站点的湍混合对风应力的响应要比对流速的响应迅速。

［1］吴立新，荆钊，Steve Riser，等.利用Agro浮标估计南大洋混合的时空变化 ［J］.中国基础科学·研究进展，2012，4：20-21.

［2］Egbert G D，Ray R D.Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data ［J］.Nature，2000，405（15）：775-778.

［3］钟贻森.黄东海湍流混合与双扩散现象及其季节变化 ［D］.青岛：中国海洋大学海洋环境学院，2009.

［4］刘志宇.强潮驱陆架海中的湍流与混合 ［D］.青岛：中国海洋大学海洋环境学院，2009.

［5］卢著敏，陈桂英，尚晓东.南海北部中深层细结构混合研究 ［J］.热带海洋学报，2009，28（3）：21-28.

［6］Su J L，Pan Y Q.On the shelf circulation north of Taiwan［J］.Acta Oceanol Sin，1987，6（Suppl I）：1-20.

［7］匡晓迪，郭心顺，范洪涛.CTD资料预处理规范化的探讨 ［J］.海洋技术，2009，28（2）：33-36.

［8］Ann Gargett And Teresa Garner.Determining Thorpe Scales from Ship-Lowered CTD Density Profiles［J］.Journal Of Atmospheric And Oceanic Technology，2008，25：1657-1670.

［9］Thorpe S A.Turbulence and mixing in a Scottish loch［J］.Phil Trans R Soc Lond A，1977，286：125-181.

［10］冯士笮，李凤岐，李少菁.海洋科学导论［M］.北京：高等教育出版社，1980.

［11］国家技术监督局.GB12763.7-91-1992.海洋调查规范—海洋调查资料处理［S］.北京：中国标准出版社，1992.

［12］汪嘉宁，魏皓，李伟.东海内陆架春季跃层和内波影响下的环境要素分布 ［J］.海洋与湖沼，2012，43（3）：644-648.

［13］Dillon T M.Vertical overturns：a comparison of Thorpe and Ozmidov length scales ［J］.Journal of Geophysical Research，1982，87（C12）：9601-9613.

［14］张卫华，赵铭军.指标无量纲化方法对综合评价结果可靠性的影响极其实证分析 ［J］.统计与信息论坛，2005，20（3）：33-36.

［15］刘天然，魏皓，赵亮，等.北部湾春季季风转换时期两潜标站余流分析 ［J］.热带海洋学报，2010，29（3）：10-16.

［16］Lueck R G，Lu Y Y.The logarithmic layer in a tidal channel［J］.Contin.Shelf Res，1997，17：1785-1801.