旋量凝聚体中偶极作用的平均场效应

王红梅

（太原师范学院 物理系，山西 太原030012）

0 引 言

1998年，MIT小组首次在纯光阱中实现了23Na的玻色爱因斯坦凝聚体（Bose-Einstein con-densate，BEC），释放了原子由于具有超精细自旋而存在的内部自由度，相当于第一次实现了旋量BEC［1］.随后实验上相继实现了自旋-1和2的23Na和87Rb凝聚［2-4］及自旋-3的52Cr凝聚［5］.具有自旋的超冷原子间存在短程各向同性的自旋交换作用和长程各向异性的磁偶极-偶极相互作用.这两种相互作用以及它们之间的竞争引起了各种丰富的磁效应.目前，偶极旋量BEC的理论研究主要集中于较简单的自旋-1或偶极作用较强的自旋-3情况.本文主要介绍偶极自旋-1BEC在平均场方法下的基态相图，然后用这种方法分析并比较自旋-2和混合自旋-1凝聚体中的偶极效应.以此研究偶极作用的普遍性质及在各旋量凝聚体中的具体表现，有助于实验上量子磁相变的探测及技术上磁效应的应用.

1 模 型

考虑N个自旋为f的玻色冷原子组成的系统.由于自旋，两两原子间具有自旋交换作用，此作用可以用接触赝势表示为

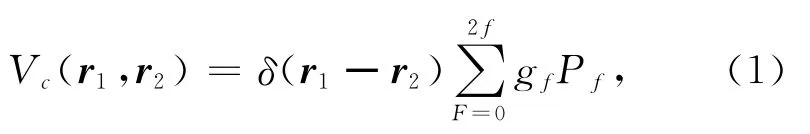
式中：r1，r2为两原子的位置；Pf是对应自旋f的投影算符，不同f时Pf有不同的具体形式；相互作用参数gf=4πh2af／M，af是f通道的s-波散射长度，M是原子质量［6］.令＾ψα（r）（α=0，…，±f）为场算符，它表示在位置r处湮灭一个磁量子数为α的玻色子，上述自旋交换作用对应的哈密顿量为

自旋使得原子具有偶极矩μ=-gμBF，这里g为朗德因子，μB为玻尔磁子，F=（Fx，Fy，Fz）表示自旋角动量，其矩阵元为Fαβ.两两原子间便存在偶极-偶极相互作用，其作用势为

式中：r12=r1-r2，e=r12／|r12|；μ0是真空磁导率.令cd=μ0g2μ2B／（4π），偶极相互作用部分的哈密顿量便表示为

当粒子数N较大时，可以采用平均场方法并作单模近似（简称为平均场近似），即令＾ψα（r）≡φ（r）ζα，这 里φ（r）满 足 粒 子 数 归 一 化 条 件满足自 旋守 恒 条 件

平均场近似下偶极作用哈密顿量为

下面给出不同自旋情况下系统的总哈密顿量形式并分析其基态性质.

2 自旋-1BEC

对于f=1原子，Vc=c0+c2F1·F2且c0=（g0+2g2）／3，c2=（g2-g0）／2［6］.平均场近似下，自旋交换作用哈密顿量为

令（c2／2）∫d r|φ（r）|4=c并忽略自旋无关c0项，系统总自旋相关哈密顿量为

这里考虑的是总自旋相关能量，忽略了原子的动能、外势能等.

利用自旋-1矩阵和并令2θ0，可以得到自旋相关的能量泛函

引入拉格朗日乘子λ，对泛函X=H1（x，y，z）-λg（x，y，z）进行最小化，并利用守恒条件g（x，y，z）=x2+y2+z2-1=0，便 得 到 全 部可能的自旋相和相应的能量.当自旋态为eiθ+（1，1，0）和eiθ-（0，0，1）时能量为e+2d；当自旋态为时能量为0；当自旋态 为时 能 量 为这里

由此得到，不考虑偶极作用时，d=0，系统只有两个相，相边界为c=0，见图1（a）.当c＞0，磁矩m=x2-z2=1，系统处于铁磁相（F）；当c＜0，磁矩m=x2-z2=0，系统处于反铁磁相或极化相（P）.考虑偶极作用d≠0，则会出现三个相.偶极作用解除了铁磁态的简并，将F相分成两个相，易于平面各向异性的相F1和易于轴向各向异性的相F2，相边界为d=0.相F1与相P的边界为c-d=0，相F2与相P的边界为c+2d=0，如图1（b）.这与文献［7］用量子方法得到的结果相同，偶极作用破坏了无偶极系统的旋转对称性并引入磁性各向异性.

图1 自旋-1BEC基态相图 Fig.1 Ground state phase diagram of spin-1 BEC

3 自旋-2BEC

当f=2时，自旋相互作用势成为Vc=α+βF1·F2+5γP0.平均场近似下的自旋相互作用哈密顿量为

通过对基态能量泛函极小化，可以得到当d=0时，由c1，c2参数决定了系统存在铁磁相（F）、极化相（P）和循环相（C），如图2所示.而d≠0的作用只是将c1变为c1+2d，即只是平移了F-P边界与F-C边界，而对P-C边界没有影响.对于自旋-2原子，一个争论是87Rb原子的基态处于F相还是C相.而偶极作用的效应相对比较小，见图2.它因此无益于87Rb原子的争论，但偶极作用也许对自旋-283Rb原子的基态有重大影响，因为实验中83Rb原子的c2，c1数据约为（c2，c1）=（3.2，-0.8）×10-27J，这靠近F-C边界且有较大值的d／c1≈［-0.59，1.18］.这个值是基于文献［8］中a0，2，4=83.0，82.0，81.0（aB）所作估算并假设83Rb与87Rb同样的原子数和密度.期望以后的精确实验可以验证自旋-283Rb在偶极作用下能否出现从相F到相C的转变.

图2 自旋-2BEC的基态相图 Fig.2 Ground state phase diagram of spin-2 BEC

实验上最早观察到偶极作用比较大的自旋-352Cr凝聚体的偶极效应［5］.由于自旋-1和自旋-2凝聚体中的偶极作用较弱，一直以来观察比较困难.最近Marti等人在探测自旋-187Rb的铁磁态时，发现了磁振子质量增加的现象［9］.此现象在理论上可以用偶极作用来解释［10］.该实验在旋量凝聚体的制备和束缚上采用常规的磁光阱，但在探测上采用对样品损伤较小的原位（in situ）测量技术，所以测量结果更加精确从而能将微弱的偶极效应显示出来.自旋-283Rb实验若采用此探测技术有望对上述F-C相作出判决.

4 混合旋量-1BEC

考虑两种自旋-1凝聚体的混合物，如23Na与87Rb原子的混合物.其原子数分别为N1，N2，场算符分别为＾Ψ（r），＾Φ（r）.在平均场近似下，设它们满足归一化条件不同种自旋-1原子间的自旋交换作用为

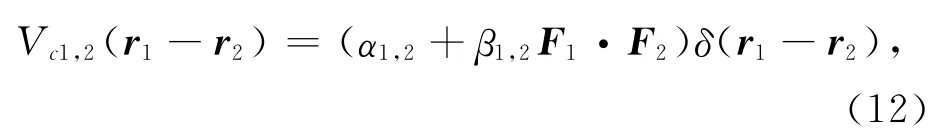
同种自旋-1原子间的偶极-偶极作用为

定义C1β1／2=c11，C2β2／2=c22，C12β／2=c12，C12γ／2=c′12，cdCd1／2=d11，cdCd2／2=d22，cdCd12／2=d12，系统的总能为

考虑一特殊情况，当〈F〉=〈Fz〉且同种原子内部相互作用为0，式（16）变为

最小化能量泛函，如果没有偶极作用，自旋交换作用会导致c′12-c12相图中由相边界c12=0和c12=c′12／3给出的PP、FF、CC和AA相［12］.前三个相类似于自旋-2BEC中的P、F和C相.只有AA相没有对应者.偶极作用的效果是将c′12-c12相图中的相边界沿c12轴平移2d12，见图3.图中只考虑了种间偶极作用、种间自旋交换作用和单体配对作用，取d12／c12=［-0.5，1.0］.这表明偶极作用对混合自旋-1BEC的影响类似于对自旋-2BEC的影响.

图3 混合偶极自旋-1BEC的基态相图 Fig.3 Ground state phase diagram for binary mixture of spin-1 BEC

5 总 结

本文研究了具有不同超精细自旋的偶极旋量BEC在不加外磁场下的基态性质，发现偶极作用破坏了无偶极系统磁性的旋转对称性，解除了铁磁相的简并，并影响到铁磁相和其它相的边界.对于自旋-187Rb原子，偶极作用的影响是需要考虑的.对于自旋-287Rb原子，偶极作用的影响虽然可以忽略，但有助于理解其它高自旋混合BEC中的偶极作用效应.

［1］Stamper-Kurn D M.Optical confinement of a Bose-Einstein condensat［J］.Phys.Rev.Lett.，1998，80：2027-2030.

［2］Gorlitz A.Sodium Bose-Einstein condensates in the F=2 state in a large-volume optical trap［J］.Phys.Rev.Lett.，2003，90：090401-090404.

［3］Schmaljohann H.Dynamics of F=2 spinor Bose-Einstein condensates［J］.Phys.Rev.Lett.，2004，92：040402-040405.

［4］Kuwamoto T.Magnetic field dependence of the dynamics of87Rb spin-2 Bose-Einstein condensates［J］.Phys.Rev.A，2004，69：063604-063609.

［5］Griesmaier A.Bose-Einstein condensation of chromium［J］.Phys.Rev.Lett.，2005，94：160401-160404.

［6］Ho T L.Spinor bose condensates in optical trap［J］.Phys.Rev.Lett.，1998，81：742-745.

［7］Yi S，You L，Pu H.Quantum phases of dipolar spinor condensates［J］.Phys.Rev.Lett.，2004，93：040403-040406.

［8］Ciobanu C V，Yip S K，Ho T L.Phase diagrams of F=2 spinor Bose-Einstein condensates［J］.Phys.Rev.A，2000，61：033607-033613.

［9］Marti G E.Coherent magnon optics in a ferromagnetic spinor Bose-Einstein condensate［J］.Phys.Rev.Lett.，2014，113：155302-155307.

［10］Saito H，Kunimi M.Energy shift of magnons in a ferromagnetic spinor-dipolar Bose-Einstein condensate［J］.Phys.Rev.A，2015，91：041603-041608.

［11］Xu Z F，Zhang Yunbo，You Y.Binary mixture of spinor atomic Bose-Einstein condensates［J］.Phys.Rev.A，2009，79：023613-023618.

［12］Ueda M，Kawaguchi Y.Spinor Bose-Einstein condensates［J］.Physics Reports，2012，520：253-364.