调和Bergman空间上两个Toeplitz算子的乘积问题

杨静宇，王晓英

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

调和Bergman空间上两个Toeplitz算子的乘积问题

杨静宇，王晓英

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

本文讨论调和Bergman空间上以拟齐次函数为符号的Toeplitz算子的乘积问题.

拟齐次函数；径向函数；调和Bergman空间；Toeplitz算子

1 引言

dA表示单位圆盘D上正规化的Lebesgue面积测度，L2(D,dA)是在D上平方可积的函数按内积

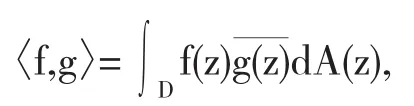
构成的Hilbert空间.L2h是由L2(D,dA)上的调和函数全体构成的闭子空间.

设u∈L∞(D,dA),在L2h上定义以u为符号的Toeplitz算子Tu为

因为L2h上的点赋值泛函是有界线性泛函，所以对于任意的z∈D,存在着唯一的函数Rz∈L2h使得

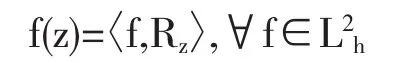
设P为L2到L2a上的正交投影，则对于任意f∈L2(D,dA)有

设φ是D上的函数，若φ(z)=φ(|z|),则φ为径向函数.若f(reipθ)=eipθφ(r),其中φ(z)=φ(|z|),那么称f为P阶拟齐次函数.

1964年，Brown和Halmos[1]在Hardy空间证明了TfTg=Th当且仅当（1）g是解析的，（2）f是余解析的.他们还给出，在这两种情况下h=fg.在Bergman空间中，这两个条件是充分条件但不是必要条件.Ahernh和Cuckovic[2]证明了Bergman空间L2a上以调和函数为符号的Toeplitz算子仍有Brown-Halmos型结果.随后Louhichi，Strouse和Zakariasy[3]给出了两个拟齐次Toeplitz算子的乘积仍是Toeplitz算子的充分必要条件.而Louhichi和Zakariasy[4]则在L2a上刻画了拟齐次函数为符号的Toeplitz算子的交换性.研究拟齐次函数为符号的Toeplitz算子的主要原因是对于L2(D,dA)中的任意函数f都有极分解

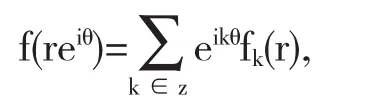
其中fk是L2([0,1],rdr)中的函数.

调和Bergman空间L2h上的Toeplitz算子理论与Bergman空间上的Toeplitz算子理论有很大的区别.例如Choe和Lee[5]证明了L2h上两个解析Toeplitz算子只有当他们的符号函数线性相关时才能交换，但在Bergman空间上两个解析Toeplitz算子总是可交换的.本文将考察L2h上两个拟齐次Toeplitz算子的乘积何时为Toeplitz算子.

2 预备知识

首先介绍径向函数的Mellin变换

设函数φ∈L1[0,1],那么φ的Mellin变换定义为

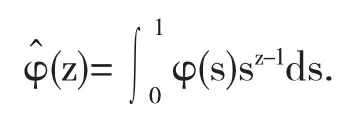
引理2.1 设p∈Z,φ是有界径向函数，那么对每一个k∈N有，

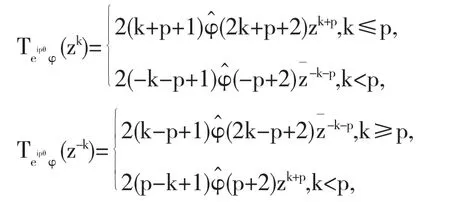
注2.2 设p,s∈Z，由引理2.1知r|s|eisθ经阶为p的Toeplitz算子映射后的像是λp,sr|p+s|ei(p+s)θ其中λp,s是常数.

引理2.3 设f是D上的有界径向函数，那么下列条件等价

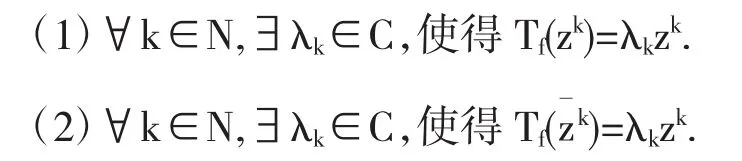
定理2.4 设f是{z:Rez＞0}上的有界解析函数并且在点z1,z2,…上取值为零，若z1,z2,…满足

那么f在{z:Rez＞0}上恒等于零.

注2.5 我们将用此定理给出，若φ∈L1([0,1], rdr)并且存在序列(nk)k≥0⊂N满足

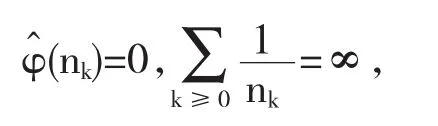
那么对所有的z∈{z:Re＞2}都有φ^(z)=0进一步得到φ=0.

3 定理的证明

首先介绍一个函数的径向化函数.设f是D上有界函数，则f的径向化函数定义为

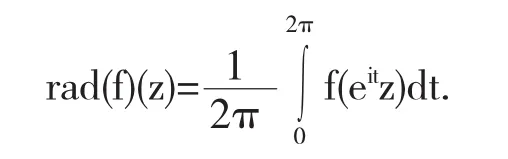
显然，f是径向函数当且仅当rad(f)=f.

定理3.1 设P∈D，f是D上的有界函数，那么下面的结论是等价的

（1）∀k∈N,∃λk∈C，使得Tf(rkeikθ)=λkr|k+p|eiθ(k+p)

（2）f是p阶拟齐次函数，

定理3.2 设f1,f2是D上阶数为k1和k2的两个有界拟齐次函数.如果存在有界函数h使得Tf1Tf2=Th，那么h是阶数为k1+k2的拟齐次函数.

定理 3.3 设l1,l2＞0并且k1,k2∈Z，那么是一个Toeplitz算子当且仅当k1=k2=0.此时

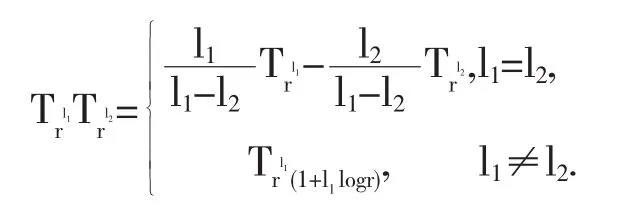
〔1〕.A.Brown and P.R.Halmos,Algebraic properties of Toeplitz operators[J],J.Reine Angew.Math.213 (1964),89–102.MR0160136(28: 3350).

〔2〕P.Ahern andˇZ.ˇCuˇckovi′c,A theorem of Brown-Halmos type for Bergman space Toeplitz operators[J],J.Funct.Anal.187(2001), 200–210.MR1867348(2002h:47040).

〔3〕I.Louhichi,E.Strouse and L.Zakariasy, Products of Toeplitz operators on the Bergman space[J],Integral Equations Operator Theory 54 (2006),525–539.MR2222982(2007a:47033).

〔4〕I.Louhichiand L.Zakariasy,On Toeplitz operatorswith quasihomogeneous symbols[J], Arch.Math.85(2005),248–257.MR2172383 (2006e:47061).

〔5〕B.R.Choe and Y.J.Lee,Commuting Toeplitz operators on the harmonic Bergman spaces[J], Michigan Math.J.46(1999),163–174.MR1682896(2000a:47054).

O177.1

A

1673-260X（2015）12-0003-04

内蒙古自治区高等学校科学研究项目（NJZY13298）