调和h-凸函数和调和平方s-凸函数的 Fejér和Hermite-Hadamard型不等式

时统业，周国辉（海军指挥学院 信息系，南京 211800）

调和h-凸函数和调和平方s-凸函数的 Fejér和Hermite-Hadamard型不等式

时统业，周国辉
（海军指挥学院 信息系，南京 211800）

利用调和h-凸函数和调和平方s-凸函数的定义以及s-凸函数、调和s-凸函数、调和平方s-凸函数三者之间的相互关系，建立了调和h-凸函数和调和平方s-凸函数的Fejér 型和 Hermite-Hadamard 型不等式.

调和h-凸函数； 调和平方s-凸函数； s-凸函数； 调和s-凸函数； Fejér和Hermite-Hadamard型不等式

1 预备知识

文[1[引入了调和h-凸函数的概念．

定义1[1］集合Ω⊆（0，+∞）称为调和凸集，若对任意x，y∈Ω和任意t∈[0，1[，有

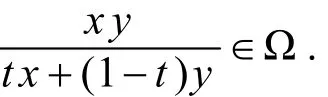
定义2[1］设h：[0，1[→ℝ是非负函数，Ω⊆（0，+∞），函数f：Ω→ℝ称为调和h-凸函数，若对任意x，y∈Ω和任意t∈[0，1[，有

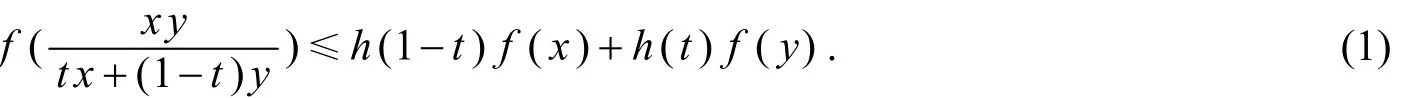
若式（1）的不等式反向，则f称为调和h-凹函数．

调和h-凸函数是调和凸函数[2］（h（t）=t），第二类调和s-凸函数[1］（h（t）=ts），调和P-凸函数[1］（h（t）=1），调和Godunova-Levin函数[1］（h（t）=），第二类调和s-Godunova-Levin函数[1］（h（t）=）的推广．

文[1[和[2[分别建立了调和凸函数和调和h-凸函数的Hermite-Hadamard型不等式．

定理1[2］设Ω⊆（0，+∞），f：Ω→ℝ是调和凸函数，a，b∈Ω，a＜b．若f在[a，b[上勒贝格可积，则有

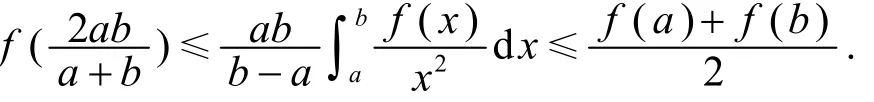
定理2[1］设I⊆（0，+∞），h：[0，1[→ℝ是非负函数，且h2）≠0，f：I→ℝ是调和h-凸函数，a，b∈I，a＜b．若f在[a，b[上勒贝格可积，则有

定义3[3］设[a，b］｛0｝，称函数g：[a，b[→ℝ是关于直线x=调和对称的，若对任意x∈[a，b[，有

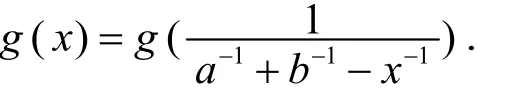
定义4 设[a，b[⊆ℝ｛0｝，称函数g：[a，b[→ℝ是关于直线x=调和平方对称的，若对任意x∈[a，b[，有

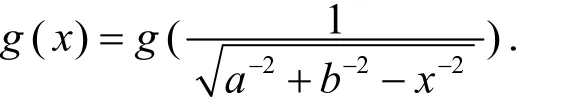
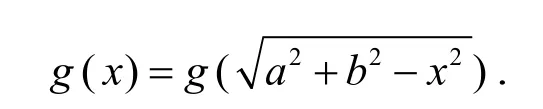
文[4[给出了调和凸函数的Fejér和Hermite-Hadamard型不等式．

定理3[4］设f：I→ℝ是调和凸函数，a，b∈I，a＜b，p：[a，b[→ℝ是非负可积函数，且关于直线x=调和对称．若f在[a，b[上勒贝格可积，则有

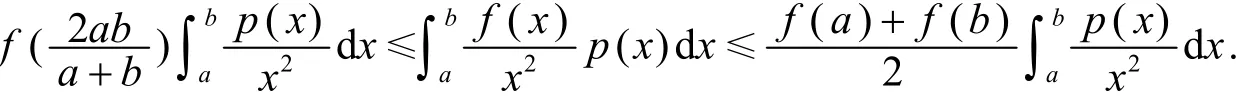
注： 若f是调和凹函数，则定理1～定理3的不等式反向．

文[5[引入了第二类调和平方凸（凹）函数的概念，文[6[中引入了第二类调和平方s-凸（凹）函数的概念． 定义6[6］设I⊆（0，+∞），s∈（0，1[，f：I→（0，+∞），若对任意x1，x2∈I和任意t∈[0，1[，有

则称f（x）为I上的调和平方s-凸函数．若不等式（2）反向，则称f（x）为I上的调和平方s-凹函数．

本文的目的之一就是建立调和h-凸函数的Fejér和Hermite-Hadamard型不等式．另一个目的是建立调和平方s-凸函数的Hermite-Hadamard型不等式．

引理1[6］设I⊆（0，+∞），τ：x→x2是单调递减函数，τ（I）=I-2，s∈（0，1[， f：I→（0，+∞），则f为I上的调和平方s-凸函数的充要条件是函数（f））-2为I-2上的s-凹函数．

引理2 设I⊆（0，+∞），s∈（0，1[，ψ：I →（0，+∞），φ（x）=xsψ （x），则ψ是I上的第二类调和s-凸函数的充要条件为φ是I上的第二类s-凸函数．

证明 与文[7[引理5的证明过程类似，这里略去．

2 主要结果

定理4 设h：[0，1[→ℝ是非负可积函数，Ω⊆（0，+∞），f ：Ω→ℝ是调和h-凸函数，a，b∈Ω，a＜b，p：[a，b[→ℝ是非负可积函数，且关于直线x=2ab调和对称．若f在[a，b[上勒贝格可积，则有 a+b

故式（3）的左边部分得证．

故式（4）的右边部分得证．

推论5.1 设I⊆（0，+∞），s∈（0，1[，f：I→（0，+∞）是I上的调和平方s-凸函数，a，b∈I，a＜b，若f在[a，b[上勒贝格可积，则有

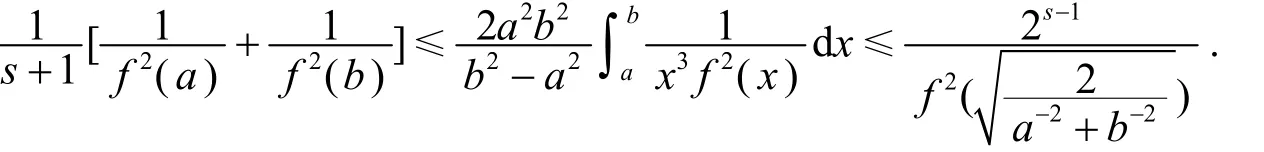
证明 在定理5中取p（x）=1即可得证．

推论5.2 设I⊆（0，+∞），f：I→（0，+∞）是I上的调和平方凸函数，a，b∈I，a＜b，p：[a，b[→ℝ是非负可积函数且关于直线x=调和平方对称．若f在[a，b[上勒贝格可积，则有

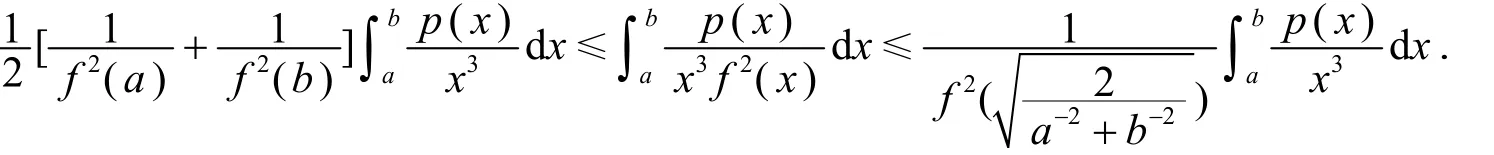
证明 在定理5中取s=1即可得证．

定理6 设I⊆（0，+∞），s∈（0，1[，a，b∈I，a＜b，q：[a，b[→ℝ是非负可积函数且关于直线x=算术平方对称．若f：I→（0，+∞）是I上的调和平方s-凸函数，且f在[a，b[上勒贝格可积，则有

再将θ（x）和p（x）代入上式并利用积分变量代换，则式（5）得证．

定理7 设s∈（0，1[，f：[a，b[⊆（0，+∞）→ℝ是[a，b[上的第二类调和s-凸函数，p：[a，b[→ℝ是非负可积函数，且关于直线x=a+b 对称．若f在[a，b[上勒贝格可积，则有 2

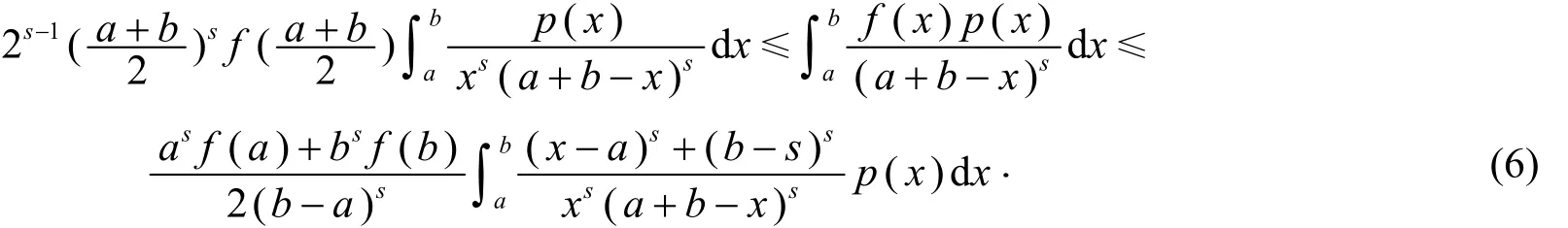
证明 由引理2知xsf（x）是第二类s-凸函数，于是对任意x，y∈[a，b[，t∈[0，1[，有

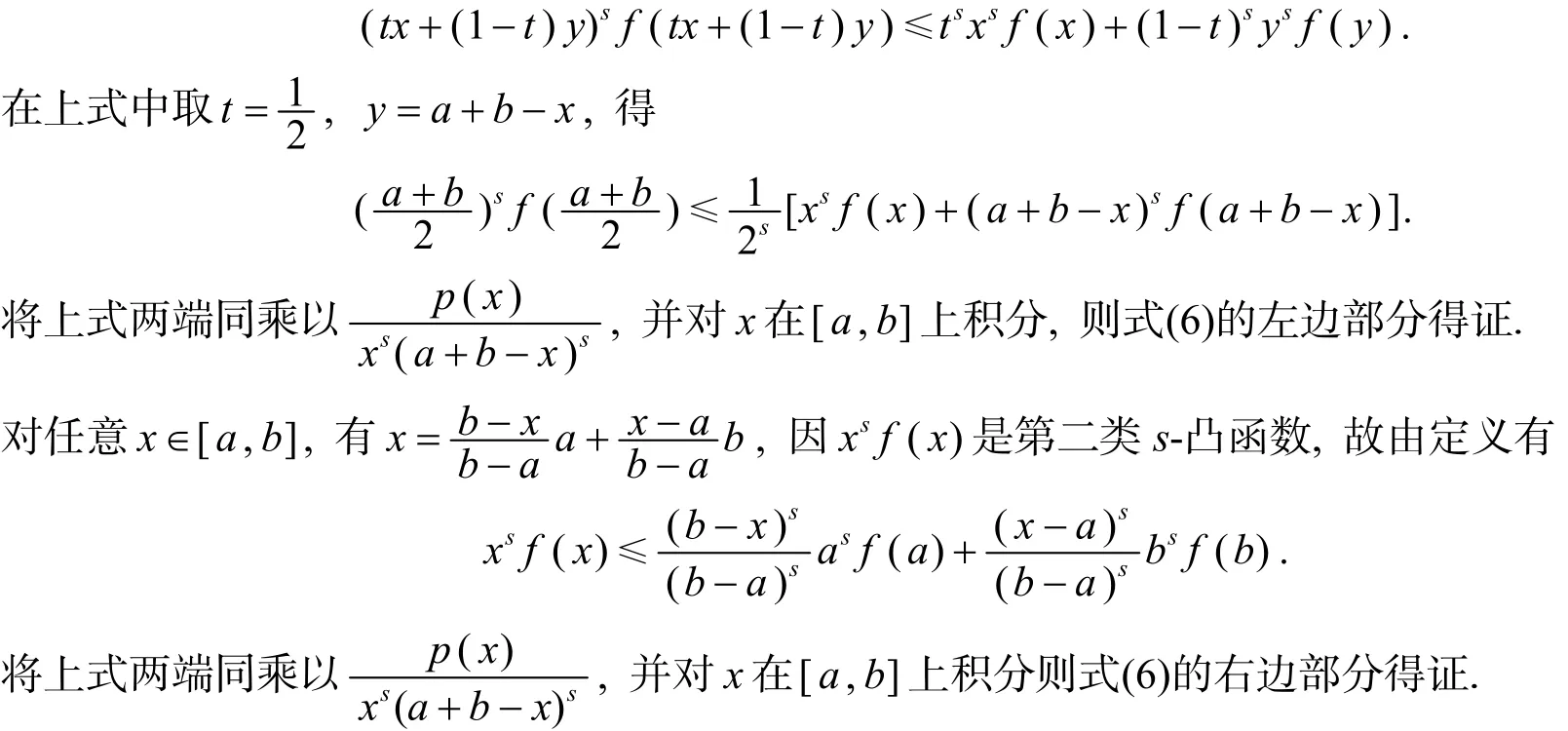
定理8 设I⊆（0，+∞），s∈（0，1[，a，b∈I，a＜b．若f：I→（0，+∞）是I上的调和平方s-凸函数，且f在[a，b[上勒贝格可积，则有

[1]Noor M A，Noor K I，Awan M U，et al. Some integral inequalities for harmonically h-convex functions[J[. University Politehnica of Bucharest Scientific Bulletin-Series A-Applied Mathematics and Physics，2015，77（1）： 5～16

[2]İşcan İ. Hermite-Hadamard type inequalities for harmonically convex functions[J[.Hacettepe Journal of Mathematics and Statistics，2014，43（6）： 935～942

[3]Turhan S，İşcan İ. Some new Hermite-Hadamard-Fejér type inequalities for harmonically convex functions[EB/OL[. https：//www.researchgate.net/ publication/287814838

[4]Chen Feixiang，Wu Shanhe. Fejér and Hermite-Hadamard type inequalities for harmonically convex functions[J[. Journal of Applied Mathematics，Volume 2014，Article ID 386806

[5]宋振云，陈少元. 调和平方凸函数及其Jensen型不等式[J[. 首都师范大学学报（自然科学版），2015，36（3）： 7～14

[6]宋振云. 调和平方s-凸函数及其Jensen型不等式[J[.数学的实践与认识，2016，46（3）： 279～284

[7]时统业，王 斌. 与HA-凸函数有关的若干不等式[J[．湖南理工学院学报（自然科学版），2015，28（4）： 1～5，36

SHI Tong-ye，ZHOU Guo-hui
（Department of Information，PLA Naval Command College，Nanjing 211800，China）

With the aid of the definition of harmonically h-convex functions and harmonic square s-convex functions and the relationship among s-convex functions，harmonically s-convex functions and harmonic square s-convex functions，Fejér and Hermite-Hadamard type inequalities for harmonically h-convex functions and harmonic square s-convex functions were obtained．

harmonically h-convex functions，harmonic square s-convex functions，s-convex functions，harmonically s-convex functions，Fejér and Hermite-Hadamard type inequalities

O178

A

1672-5298（2016）02-0001-05

2016-03-25

时统业（1963-），男，河北张家口人，硕士，海军指挥学院信息系副教授. 主要研究方向： 基础数学