空气中PM2.5反应扩散方程的模拟

郭慧敏，黄冠佳，房少梅*

（华南农业大学数学与信息学院，广东广州510642）

空气中PM2.5反应扩散方程的模拟

郭慧敏，黄冠佳，房少梅*

（华南农业大学数学与信息学院，广东广州510642）

根据实际情况，研究空气中细颗粒物（PM2.5）的污染问题。首先，建立多维情况下具有初值条件的PM2.5反应扩散方程；其次，利用偏微分方程中常用的方法——Fourier变换，求出具有初值条件的反应扩散方程的解；最后，使用MATLAB软件对已经求出的解进行模拟，分别拟合出水平面与垂直面上PM2.5浓度值的扩散情况，以及PM2.5浓度值与时间的变化情况。

PM2.5；反应扩散方程；Fourier变换；数值模拟

随着社会的快速发展和生活质量的提高，人们越来越重视空气污染问题。近年来，大气污染问题，尤其是细颗粒物（PM2.5）污染问题日益严峻。PM2.5是指直径小于等于2.5μm的污染物颗粒，其粒径小，表面积大，容易富集空气中的有机污染物、酸性氧化物和有毒重金属等等，从而导致人体各系统疾病的发生。此外，PM2.5还会降低大气能见度，吸收和反射太阳辐射，影响城市大气的光学性质与热平衡，导致农作物产量降低。因此，如何控制和治理PM2.5已成为刻不容缓的民生问题，这也是当前社会的热点问题和难点问题。

在过去20多年里，国内外学者对PM2.5问题展开了大规模的研究，主要涉及PM2.5对人体健康的影响、源解析、污染特征、监测技术、脱除技术等方面［1］。早在1989年，美国研究人员Dockery等［2］就已经针对空气中可吸入颗粒物对健康儿童呼吸道的影响进行了研究，结果显示：儿童的慢性咳嗽、支气管炎等疾病与PM15、PM2.5等有关。部分文献［3-5］进一步从医学角度研究了空气中颗粒物，特别是PM2.5的浓度与人体健康的关系，结果表明：PM2.5与心肌梗塞、中风、心力衰竭等疾病有着密切的关系。2001年9月至2002年1月，Sawant等［6］在加利福尼亚Mira Loma地区对PM2.5的化学组分进行研究，发现Mira Loma地区的有机碳浓度高于美国其他城市。2012年，Velasco等［7］对新加坡地区的空气质量进行了研究，数据表明：唯有PM2.5不满足美国环境保护署（EPA）制定的国家环境空气质量标准和世界卫生组织（WHO）制定的空气质量指南，进一步指出PM2.5是当地空气污染的主要问题和影响健康的主要原因。

在我国，针对PM2.5问题研究起步较晚，相对较早的是吴国平等［8］，他们主要针对重庆、兰州、广州和武汉，分别研究这四大城市空气中PM2.5和PM10的污染水平。2005年，王平利等［9］陈述了大气尘的研究现状，重点围绕TSP、PM10、PM2.5的物理特征、化学组成，包括其有机组成、重金属元素含量、各化学形态分布进行描述。2006年，杨书申等［10］进一步对PM2.5的物理化学特征与分析方法、健康效应、来源解析、

及其对能见度的影响等方面进行了论述，并对其研究动向进行了展望。2013年，王敏等［11］利用人工神经网络，对PM2.5的浓度进行空间预测，通过插值方法对比验证BP人工神经网络预测模型的精度。

总体而言，国内外对PM2.5的研究主要停留在对其理化性质的研究，而使用数学建模的方法，尤其是使用反应扩散方程，对PM2.5的扩散机理以及PM2.5的浓度进行预测与控制，目前还没有形成较为完整的体系。因此，本文首先根据实际情况，建立多维情况下的具有初值条件的PM2.5反应扩散方程；其次，使用泛函分析中的傅立叶（Fourier）变换，进而求出PM2.5的浓度函数；最后，针对已求出的浓度函数进行数值拟合，分别模拟PM2.5在空间与时间中的扩散情况。

1 建立空气中PM2.5的数学模型

为了解空气中PM2.5的扩散机理，需要建立多维情况下的具有初值条件的反应扩散方程。但为简化运算，需假定PM2.5在空气中各方向上的扩散系数均为D。因此，可以得出多维情况下具有初值条件的PM2.5反应扩散方程为

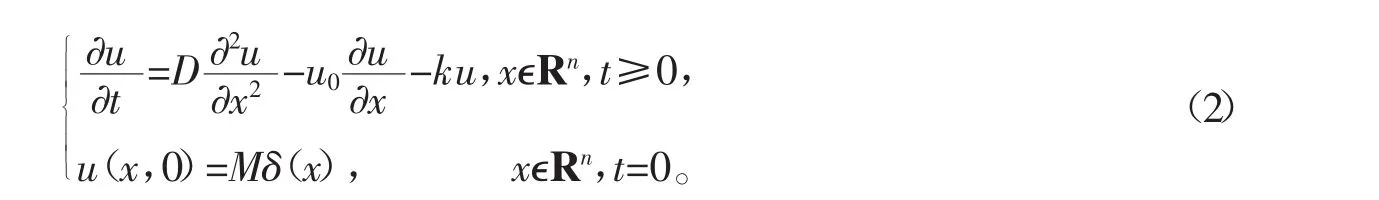
由文献［12-13］可知，反应扩散方程的基本形式为

其中，u（x，t）表示空气中PM2.5的浓度，t表示PM2.5在空气中的扩散时间，D表示PM2.5在空气中的扩散系数，x∈Rn表示PM2.5的坐标位置，u0表示风速大小，k表示PM2.5在空气中的衰减系数，M表示PM2.5最初浓度值，δ（x）在物理学中表示为δ函数，且Rn∫δ（x）d x=1。

2 基本引理

引理1［14］定义函数

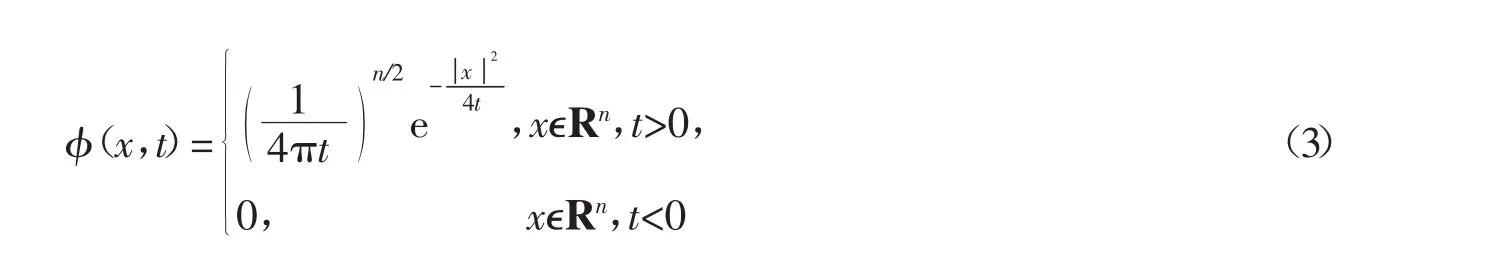
为热传导方程的基本解，其中，Rn∫φ（x，t）d x=1。

引理2［14］假设u，v∈L2（Rn），那么有：1）Rn∫uv d x=Rn∫uˆvˆd y；2）Dαu=（iy）αuˆ，对于任意的α均有Dαu∈L2（Rn）；3）（u*v）＾=（2π）n/2uˆvˆ；4）u=（uˆ）ˇ。

3 空气中PM2.5的数学模型求解

由文献［14］可知，当扩散系数D=1、风速与衰减系数均为0时，即：u0=0，k=0时，方程（2）可变为如下热传导方程

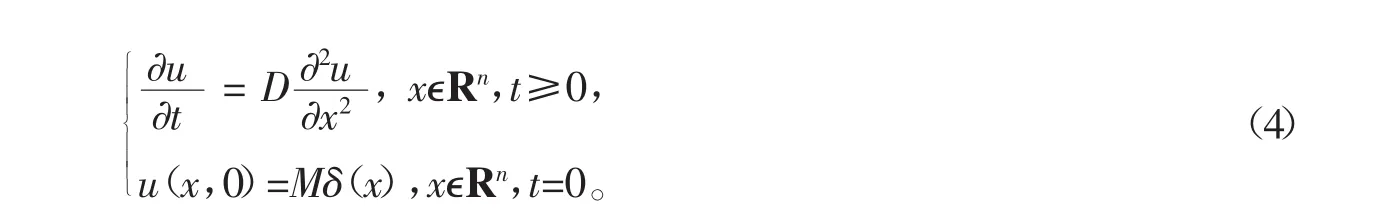
由引理1可得，方程（4）的基本解为

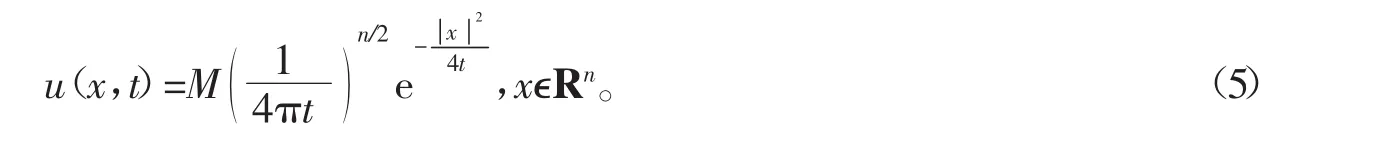
当扩散系数D≠1、风速与衰减系数均为0时，对方程（5）两端关于x分别进行Fourier变换，可得

其中，uˆ与δˆ分别表示u与δ的Fourier变换。通过常微分运算，可得

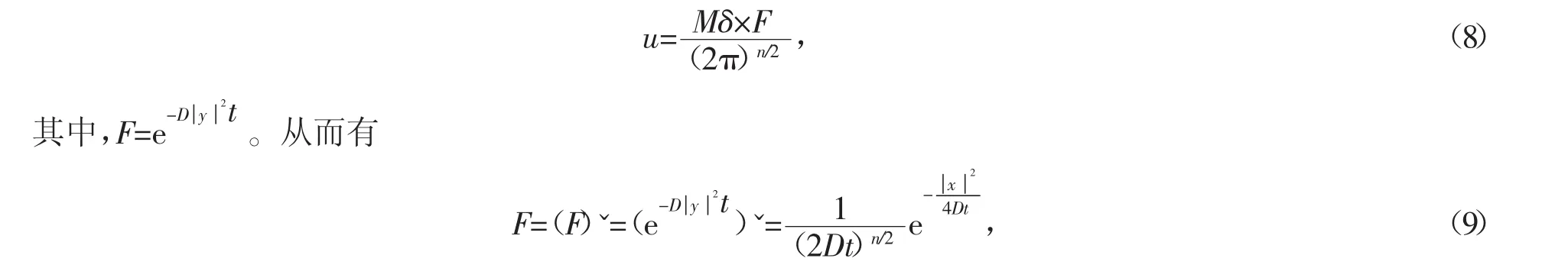
将式（9）代入式（8），以及Rn∫δ（x）d x=1，可以得到D≠1时，方程（4）的基本解为

其次，讨论扩散系数D≠1与风速u0≠0的情况。可得如下方程

其中，Rn∫δ（x）d x=1。令zi=xi-u0t，i=1，2，…，n且s=t，设N（z，s）=u（x，t），则

其中，Rn∫δ（z）d z=1。由方程（4）的基本解可知

将zi=xi-u0t，i=1，2，…，n与s=t代入方程（13），可得

最后，讨论扩散系数D≠1，风速u0≠0与衰减系数k≠0的情况。假设

将式（15）代入方程（2），可得等式两端相等，因此方程（2）的基本解为

4 数值拟合

一般而言，需要考虑空气中的PM2.5污染的实际情况，即：考虑多维情况下PM2.5的扩散机理。因此，本文考虑n=3时PM2.5的扩散情况。

需要选定PM2.5在空气中的扩散系数、衰减系数与风速。首先，由于PM2.5在空气中的扩散系数较难查找，因此需要从另一角度考虑其扩散系数。由于PM2.5主要由SO2转化而成的，因此可以使用SO2在空气中的扩散系数近似地作为PM2.5的扩散系数。根据文献［15-16］可知，SO2与空气在常压（1.013×105 Pa）与常温（293 K）下的扩散系数等于1.22×10-5m2/s。其次，PM2.5在不治理的情况下是难以消失的，因此衰减系数k可以近似地当作0，即：k= 0。最后，假设是静风或风速u0非常接近0m/s的情况。假设PM2.5的浓度初值M为1μg/cm3，扩散系数D为1.22×10-1cm2/s，衰减系数k为0，风速u0为0.1 cm/s，时间t=1 s。

首先，讨论t=1 s时，PM2.5浓度函数在水平面上的扩散图形，如图1所示。由于式（16）中的x1、x2、x3是对称的，因此图1也可以表示浓度函数在t=1 s时垂直面上的扩散图形。由图1可知，当t=1 s时，原点处浓度最高，约为0.35μg/cm3。随着水平距离的不断增加，浓度值在不断下降。同时，由于x1、x2、x3在式（16）中是对称的，因此PM2.5的浓度值在垂直面上的扩散情况与水平面上的情况是一致的。

其次，讨论在同一点处PM2.5浓度值随着时间t变化的情况，如图2所示。现假设该点为原点，即x1=x2=x3=0，从图2的图形变化形式可知，随着时间t的不断增加，PM2.5浓度值按指数形式进行递减，且递减的速度越来越快；当时间无限增大时，PM2.5浓度值将无限接近于0μg/cm3，但是无法达到0 μg/cm3。

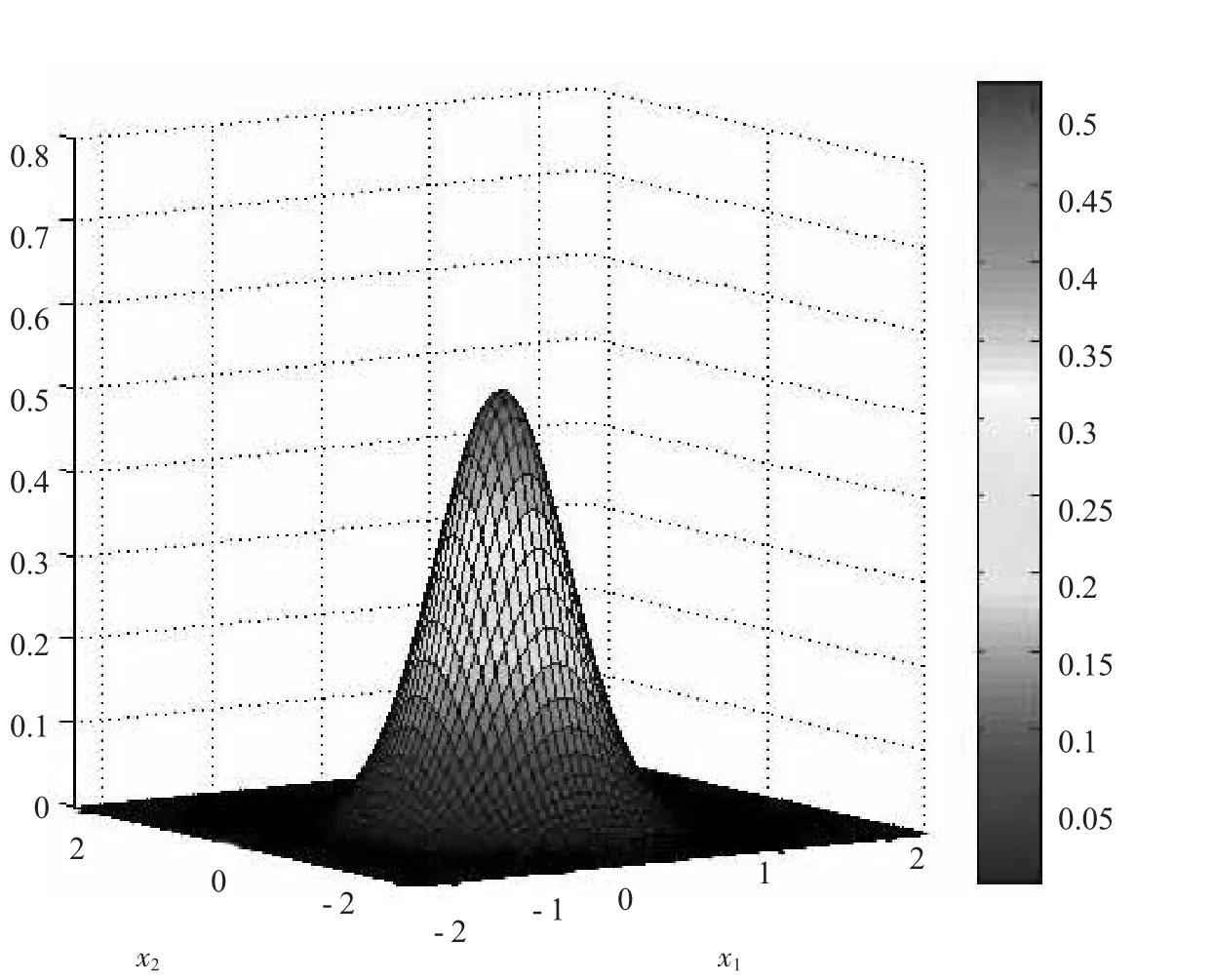
图1 PM2.5在t=1 s时水平（垂直）面上的浓度扩散图

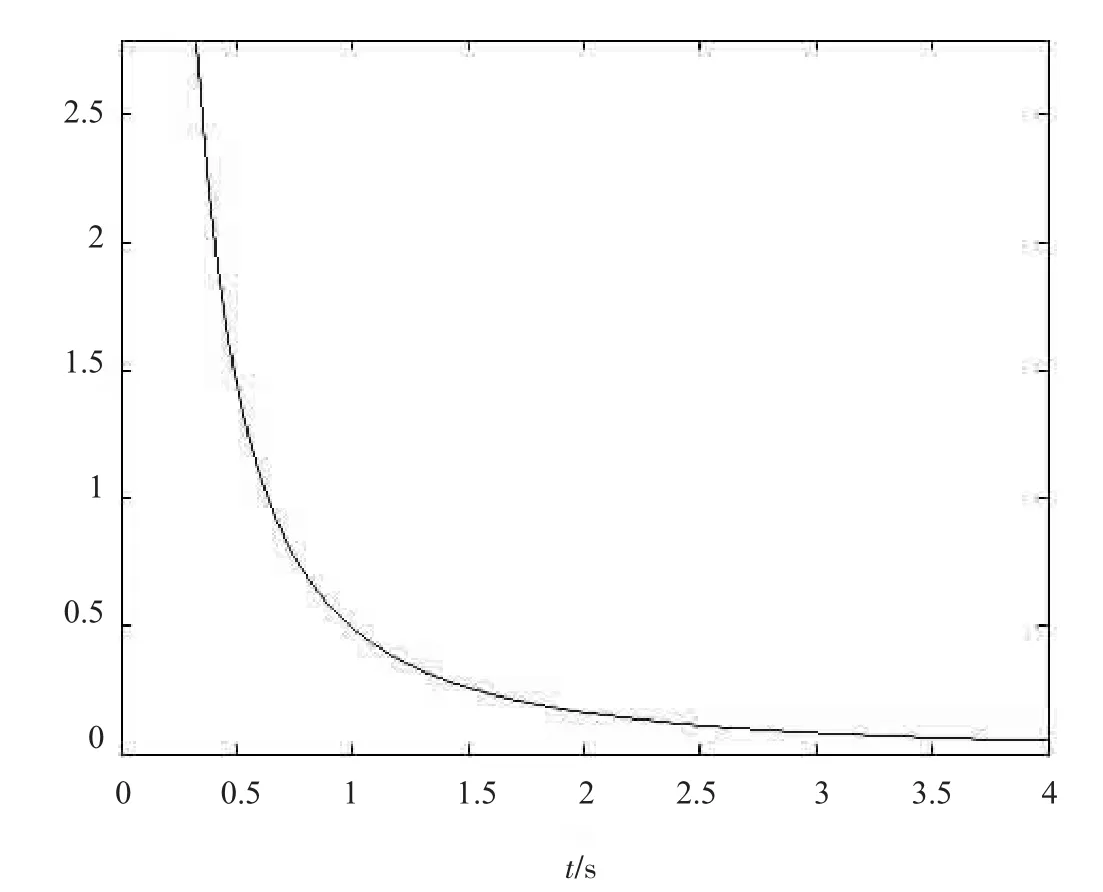
图2 PM2.5浓度值随时间t变化的扩散图

综合图1与图2，可以知道PM2.5在中心区域的浓度是最高的，影响程度也是最大的，但是随着水平距离与垂直距离的不断增长，PM2.5浓度不断下降，且下降的速度按指数形式不断增加，即：PM2.5的影响范围虽然在不断地扩大，但对于远离PM2.5中心点的地方，PM2.5影响的程度相当少；同时，PM2.5浓度随着时间的增加而不断按指数形式下降，最后能接近0μg/cm3。

［1］吴兑.华南气溶胶研究的回顾与展望［J］.热带气象学报,2003,19（S1）:145-151.

［2］DOCKERY D W,SPEIZER F E,STRAM D O.Effects of inhalable particles on respiratory health of children［J］.The American review of respiratory disease,1989,139（3）:587-594.

［3］SIOUTAS C,DELFINO R J,SINGH M.Exposure assessment for atmospheric ultrafine particles（UFPs）and implications in epidemiologic research［J］.ENVIR ONMENTAL HEALTH PERSPECTIVES,2005,113（8）:947-955.

［4］LIPPMANN M,SCHLESINGER R B.Toxicological bases for the setting of health-related air pollution standards［J］.Annual review of public health,2000,21:309-333.

［5］MUSTAFIC H,JABRE P,CAUSSIN C,et al.Main Air Pollutants and Myocardial Infarction A Systematic Review and Meta-analysis［J］.JAMA-JOURNAL OF THE AMERICAN MEDICAL ASSOCIATION,2012,307（7）:713-721.

［6］SAWANT A,NA K,ZHU X K,et al.Chemical characterization of outdoor PM2.5and gas-phase compounds in Mira Loma, California［J］.ATMOSPHERIC ENVIRONMENT,2004,38（33）:5517-5528.

［7］VELASCO E,ROTH M.Review of Singapore's air quality and greenhouse gas emissions:Current situation and opportunities［J］.JOURNAL OF THE AIR＆amp;WASTE MANAGEMENT ASSOCIATION,2012,62（6）:625-641.

［8］吴国平,胡伟,滕恩江,等.我国四城市空气中PM2.5和PM10的污染水平［J］.中国环境科学,1999,19（2）:133-137.

［9］王平利,戴春雷,张成江.城市大气中颗粒物的研究现状及健康效应［J］.中国环境监测,2005,21（1）:83-87.

［10］杨书申,孙珍全,邵龙义.城市大气细颗粒物PM2.5的研究进展［J］.中原工学院学报,2006,17（1）:1-5,25.

［11］王敏,邹滨,郭宇,等.基于BP人工神经网络的城市PM2.5浓度空间预测［J］.环境污染与防治,2013,35（9）:63-66, 70.

［12］李婷,孙丽男.基于反应扩散方程的水污染模型解析解的模拟［J］.吉林化工学院学报,2012,29（7）:88-91.

［13］李婷,孙丽男.一类基于反应扩散方程的连续源水污染模型［J］.吉林化工学院学报,2012,29（9）:90-93.

［14］EVANS L C.Partial differential equations,graduate studies in mathematics［M］.Providence,Rhode Island:American mathematical society,1988:184.

［14］何潮洪,窦梅,钱栋英.化工原理操作型问题的分析［M］.北京:化学工业出版社,1998.

［15］王志魁.化工原理［M］.北京:化学工业出版社,1987.

【责任编辑：王桂珍foshanwgzh@163.com】

The simulation of reaction diffusion equation about PM2.5in the air

GUO Hui-min,HUANG Guan-jia,FANG Shao-mei

（College of Mathematics and Informatics,South China Agricultural University,Guangzhou 510642,China）

According to the actual situation,this paper studies air pollution problem about PM2.5in the air.First of all,establishing a multi-dimensional reaction diffusion equations of PM2.5with initial conditions;Secondly,the use of Fourier transform can obtain the solutions of reaction diffusion equation with initial conditions,which is the common method in partial differential equation;Finally,the PM2.5diffusion on the horizontal and vertical surface can be obtained by the MATLAB programming.And the PM2.5density with the changes of time can be learned at the same time.

PM2.5;reaction diffusion equation;Fourier transform;numerical simulation

X513；O242.1

A

1008-0171（2015）05-0024-05

2014-12-31

国家自然科学基金资助项目（11271141）

郭慧敏（1989-），女，广东广州人，华南农业大学硕士研究生。*

房少梅（1964-），女，安徽淮北人，华南农业大学教授，博士。