加权欧氏距离的聚类分析在葡萄酒质量分级中的应用

房少梅，张颖姝，马雅从，黄冠佳

（华南农业大学数学与信息学院，广东广州510642）

加权欧氏距离的聚类分析在葡萄酒质量分级中的应用

房少梅，张颖姝，马雅从，黄冠佳

（华南农业大学数学与信息学院，广东广州510642）

提出了一种新的葡萄酒质量分级方法。从葡萄和葡萄酒的理化指标、芳香物质出发，首先用逐步回归分析筛选出主要指标；然后用主成分回归分析得到各指标的权重系数；最后引入加权欧氏距离来改进聚类分析，并对葡萄酒质量进行分级。结果表明：该方法将红白葡萄酒均分为三类，分级结果合理，方法具有普适性。

葡萄酒质量分级；逐步回归；主成分回归；聚类分析；权重

以往葡萄酒质量的评价方式是以评酒员的感官评价为主，主观性较强。为了使评价结果更为客观，已有许多学者提出了基于葡萄酒理化指标的葡萄酒质量评价方式，例如，李运等［1］运用相关分析、通径分析和主成分分析等方法，得到了葡萄酒感官得分与8个葡萄酒理化指标主成分之间的回归方程；翟明娟［2］运用聚类分析方法对葡萄酒的质量进行分级；Cortez等［3］用支持向量机方法建立了葡萄酒的质量分级模型；王经民等［4］用红白葡萄酒的理化指标和葡萄酒得分进行多元回归分析，结果表明白葡萄酒用此方法得到的回归方程显著性稍差。上述研究均以独立的葡萄酒样本作为研究对象，并没有考虑酿酒葡萄或者芳香物质对葡萄酒质量的影响，而且在聚类分析中认为每种评价指标对葡萄酒质量的影响程度是相同的。针对这些问题，本文以多种葡萄酒质量之间的差异作为研究对象，综合考虑葡萄酒和酿酒葡萄的理化指标、芳香物质共202个指标，运用逐步回归分析、主成分回归分析以及加权欧氏距离的聚类分析方法，对葡萄酒的质量进行分级，得到的分级结果区分度明显，为葡萄酒质量分级提供了新的方法。本文数据来自2012年全国大学生数学建模竞赛A题［5］。

1 问题分析

葡萄酒质量的分级问题，实际上是如何根据现有的202个影响葡萄酒质量的指标对葡萄酒样本进行合理分类的问题，参考的评价指标是各酒样的平均得分。由于202个指标过多，指标之间可能具有多重共线性，并且得到各指标对葡萄酒质量的作用机理过于繁琐。若直接以酒样得分为因变量与各指标进行多元线性回归，难以保证参数估计具有实际意义，因此，将分析的主体设置为质量的差异性。根据文献［6］的结论，认为第二组评酒员的评分更可靠，并处理缺失和异常数据。然后建立逐步回归模型对202个指标进行筛选，建立主成分回归模型消除多重共线性，分析每个指标的差异性对整体质量差异性

的影响情况，为分类做好准备。

2 逐步回归模型

2.1 单指标距离的计算

定义样本i与样本j第t个指标的单指标距离为

以此来衡量样本间第t个指标的差异性。运用Matlab编程，对葡萄酒的平均得分也做相同计算，共得到203列数据。

2.2 模型的计算与结果

为了筛选出对质量差异性影响较大的指标，本文以单指标距离作为自变量，葡萄酒得分的距离作为因变量，运用SPSS16.0软件进行逐步回归分析［7］。结果表明，影响红葡萄酒质量差异性的23个主要指标为：C（D65），C11H22O2，C6H12O2，C4H7NO，C10H20O，C8H18O2，PH值，蛋白质，色泽b，葡萄总黄酮，顺式白藜芦醇，单宁，苏氨酸，蛋氨酸，C4H8O2，C3H6O，C10H20O，C7H16O，色泽c，C9H10O2，C13H12，异鼠李素，C8H18O；影响白葡萄酒质量差异性的20个主要指标为：C8H18O，C11H24，b*（+黄;-蓝），C4H8O2，C3H8O，C12H24O，C11H22O2，C10H16O，C8H14O4，C10H16O，C6H10O，C6H14O3，C9H14O，丙氨酸，葡萄总黄酮，总酚，异亮氨酸，C4H10O，C6H12O，苏氨酸。

变量参数估计t检验P值均小于0.05，拒绝原假设，假设检验通过，参数估计显著有效。两个模型F检验P值亦均小于0.05，模型显著有效，调整后的拟合优度分别达到0.633和0.671，说明红白葡萄酒整体质量差异的变化程度可分别由回归方程解释63.3％和67.1％。

3 主成分回归模型

由于红白葡萄酒的主要指标均可能具有多重共线性，因此，使用主成分分析［8］得到互不相关的各个主成分，以消除多重共线性。筛选出的主成分尽可能多地反映了原来变量的信息，并对因变量变化情况的解释程度较好。

运用SAS软件分别对红白葡萄酒进行主成分分析，初步得到红葡萄酒23个、白葡萄酒20个主成分，它们分别可以用逐步回归筛选出的23个、20个变量线性表出。然后，以葡萄酒得分间的距离作为因变量，各主成分作为自变量，运用SAS编程进行主成分回归，结果表明，所选主成分的参数估计P值均小于0.05，显著有效，并且红白葡萄酒主成分累计贡献率分别为82.6％和72.5％，说明主成分在很大程度上保留了原来自变量的信息。两个模型F检验P值均小于0.05，模型显著有效。红白葡萄酒主成分回归分析后的拟合优度分别为74.65％和76.04％，均比直接使用逐步回归分析提高10％左右。相应的回归方程可以表示为

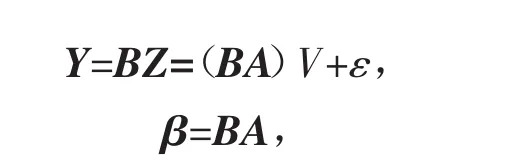
其中，V为逐步回归筛选出的主要指标；B为主成分变量的参数估计值，以行向量表示；A为主成分的载荷矩阵；β为各指标差异性权重。各指标差异性权重，表示每个指标的差异对葡萄酒整体质量差异的影响程度，权重绝对值较大的指标意味着该指标较小的差异将会引起葡萄酒整体质量较大的变动。

4 聚类分析

欧氏距离是聚类分析中使用最广泛的距离。假设有n个样本，m个指标，两个样本间的欧氏距离定义如下［9］

考虑各指标差异对葡萄酒质量差异的影响程度，本文重新定义了加权欧式距离，即

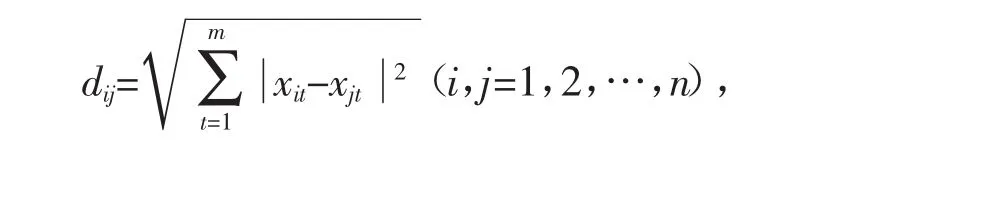
其中，βt为回归方程中各指标差异性权重，α为较大的正常数且

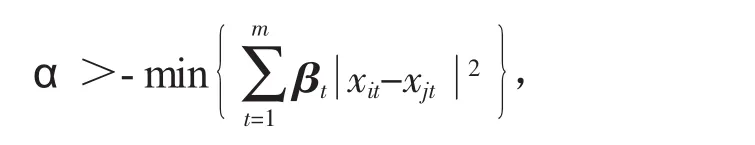
引入α既可保证距离的非负性又不影响聚类的结果。

本文采用Matlab编程实现聚类分析，将红白葡萄酒样本分为三类，结果如表1、2所示。由表1、2可知，两种葡萄酒样本的聚类效果很好，几乎所有得分相近的样本都分在同一类当中。再结合得分可知，第1类为高品质级，第2类为良好级，第3类为中等及以下级。

表1 红葡萄酒聚类分析结果

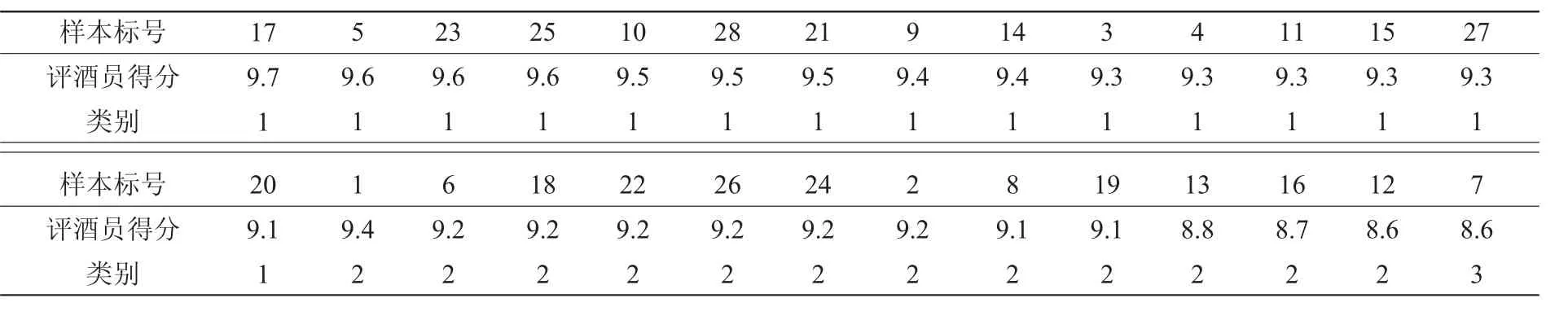
表2 白葡萄酒聚类分析结果

5 模型对比

为了更加明显地看出改进后的聚类分析算法的分级效果，本文对202个指标做标准化处理后进行无加权聚类分析，计算出每一类的得分均值，并与加权聚类分析的结果对比，如表3、4所示。

表3 红葡萄酒两种分级模型对比

表4 白葡萄酒两种分级模型对比

由表3、4可知，无加权聚类分析的三类均分极差仅为0.38和0.24，均分离差平方和仅为0.240 8和0.113 8，而加权聚类分析的三类均分极差为1和0.83，均分离差平方和为1.507 2和1.040 6，远大于改进前的聚类分析方法。与文献［4］对比，其方法更适用于红葡萄酒，但本文对红白葡萄酒质量的分级效果都很好。并且由表1、2可知，高等级的样本得分普遍高于低等级，也表明加权聚类算法使分级效果更加明显。

6 结语

本文提出了一种新的葡萄酒质量分级方法，这种方法在对葡萄酒的质量分级时优于传统的聚类分析方法。考虑了葡萄酒和酿酒葡萄的理化指标、芳香物质等202个指标对葡萄酒质量的影响，采用逐步回归的方法初步筛选出主要指标，然后用主成分回归的方法提取出主成分，并通过回归方程的系数得到各指标的差异性权重系数。加入权重系数后的聚类距离，直接将红白葡萄酒各分为三类，从而可以更好地对葡萄酒质量进行评价。新方法的优异表现是因为聚类距离体现了每个评价指标对葡萄酒质量差异的影响程度。这种加权欧式距离的聚类分析方法也适用于其他的分级问题。

当然，本文提出的葡萄酒质量的分级方法只是多种评价方法之一，影响葡萄酒质量的指标很多，其筛选尤为重要。因此，如何选取恰当的评价指标是需要进一步研究的问题。

［1］李运,李记明,姜忠军.统计分析在葡萄酒质量评价中的应用［J］.酿酒科技,2009,30（4）:79-82.

［2］翟明娟.基于聚类分析法的葡萄酒评价［J］.太原师范学院学报:自然科学版,2014,13（2）:35-40.

［3］CORTEZ P,CERDEIRA A,ALMEIDA F,et al.Modeling wine preferences by data mining from physicochemical properties［J］. Decision Support Systems,2009,47（4）:547-553.

［4］王经民,王灿,张京芳.葡萄酒质量的评价模型［J］.数学建模及其应用,2013,2（2）:72-78.

［5］全国大学生数学建模竞赛组委会.2012年全国大学生数学建模竞赛A题［EB/OL］.［2015-01-26］.http://www.mcm. edu.cn/problem/2012/2012.htm l.

［6］周义仓.2012年CUMCM A题解答评析［J］.数学建模及其应用,2013,2（1）:60-66.

［7］房少梅.数学建模理论、方法及应用［M］.北京:科学出版社,2014.

［8］任雪松,于秀林.多元统计分析［M］.2版.北京:中国统计出版社,2011.

［9］高惠璇.应用多元统计分析［M］.北京:北京大学出版社,2013.

【责任编辑：王桂珍foshanwgzh@163.com】

Application of cluster analysis with weighted euclidean distance to classification ofw inequality

FANG Shao-mei,ZHANG Ying-shu,MA Ya-cong,HUANG Guan-jia
（College of Mathematics and Informatics,South China Agricultural University,Guangzhou 510642,China）

A new method of classification of wine quality was proposed.Based on aromatic matter,physical and chemical criterion of wine and grapes,firstly,the study used the stepwise regression to select main indexes.Then obtained the weight of each index by the principal component regression.Finally,improved the cluster analysis by using weighted Euclidean distance and classed the wine quality.The results show that red wine and white wine are classified into three groups respectively by the above method.The results are reasonable and this method is universalistic.

classification of wine quality;stepwise regression;principal component regression;cluster analysis; weight

TS262.61

A

1008-0171（2015）05-0017-04

2015-03-02

国家自然科学基金资助项目（11271141）；广东省高等教育教学改革项目（GDJG20141038）

房少梅（1964-），女，安徽淮北人，华南农业大学教授，博士。