矩阵秩方法在广义逆中的应用

黄旭

（吉林大学珠海学院公共基础课教学与研究中心，广东珠海519041）

矩阵秩方法在广义逆中的应用

黄旭

（吉林大学珠海学院公共基础课教学与研究中心，广东珠海519041）

矩阵秩方法是矩阵理论中一种独特的方法，它往往能独辟蹊径，化繁为简，在矩阵理论有着重要的地位。讨论了矩阵秩方法在广义逆中的一些简单应用。

广义逆；矩阵秩；Schur补

1 预备知识

定义1一个矩阵A∈Cn×n称为Hermitian矩阵，若它的共轭转置等于它自身，即A*=A。

定义2对于一个m×n的矩阵A，若存在一个n×m的矩阵G，使得：1）AGA=A；2）GAG=G；3）（AG）T=AG；4）（GA）T=GA。则称G为A的Moore-Penrose逆，简称M-P逆，记作A+。

定义3设A∈Cn×n，矩阵X称为A的群逆，如果A满足r（A）=r（A2）且满足如下矩阵方程：1）AXA= A；2）XAX=X；3）AX=XA。我们记A的群逆为A#。其中r（）表示矩阵的秩。

下面给出一些关于矩阵秩常用的一些结论。

引理1［1-2］设A∈Cm×n，B∈Cm×k，C∈Cl×n，D∈Cl×k，则

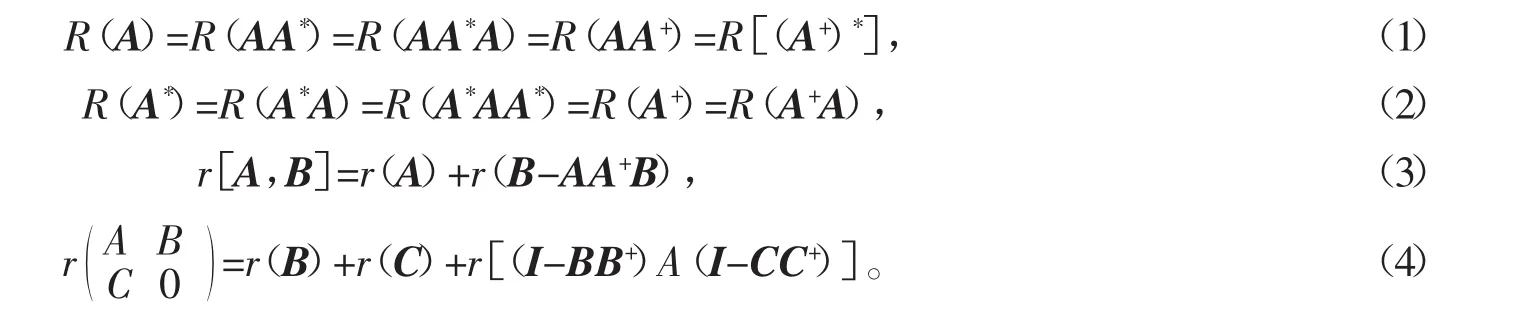
引理2［3］设A∈Cn×n，则r（A）+r（A-A3）=r（A+A2）+r（A-A2），从而A=A3当且仅当

证明由矩阵块高斯消元法有

2 主要结论

定理1设A∈Cn×n，则A+=A的充要条件是r（A）=r（A+A2）+r（A-A2）且A2是Hermitian矩阵。

证明⇒当A+=A时，A2=AA+=（AA+）*=（A2）*，从而A2是Hermitian矩阵。由引理3知A=A3⇔r（A）= r（A+A2）+r（A-A2），所以A3=AAA=AA+A=A。

⇐因为A=A3⇔r（A）=r（A+A2）+r（A-A2），所以A3=A，所以定义2中1）、2）成立。因为A2=（A2）*，所以定义2中3）、4）成立，故命题得证。

定理2设A∈Cn×n，A#存在，则A=A#的充要条件是r（A）=r（A+A2）+r（A-A2）。

证明⇒A3=AAA=AA#A=A，而A=A3⇔r（A）=r（A+A2）+r（A-A2），得证。

⇐由r（A）=r（A+A2）+r（A-A2）得到A3=A，从而定义3中1）、2）、3）成立，因为r（A2）≤r（A）=r（A3）≤r（A2），所以r（A）=r（A2），得证。

Campbell等［5］利用投影算子的理论得到了（AB）+=B+A+的一些充要条件，下面利用矩阵秩的方法给出证明。

定理3［5-6］设A∈Cm×n，B∈Cn×p，则下面几个条件是等价的：

（1）BB*A+A=A+ABB*，A*ABB+=BB+A*A；

（2）R（A*）是BB*的不变子空间且R（B）是AA*的不变子空间；

（3）A+ABB*A*=BB*A*且BB+A*AB=A*AB；

（4）A+AB=B（AB）+AB，ABB+=AB（AB）+A。

证明文献［6］已经给出（1）⇔（2）⇔（3）的证明，下面给出（2）⇔（4）的证明。

由引理3式（7）得

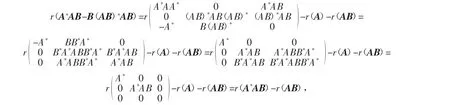
A+AB=B（AB）+AB⇔r（A+AB-B（AB）+AB）=0⇔r（A*AB）=r（AB）⇔R（A*AB）=R（AB）⊆R（B），所以A+AB= B（AB）+AB⇔R（B）是AA*的不变子空间。

同理可证ABB+=AB（AB）+A⇔R（A*）是BB*的不变子空间，故（2）⇔（4）。

推论（1）设A∈Cm×n，B∈Cn×p，则AB=0的充要条件是B+A+=0；

（2）设A∈Cn×m，B∈Cn×p，则A+B=0的充要条件是A*B=0。

证明（1）由文献［5］有（AB）+=（A+AB）+（AAB+）+，从而AB=0⇔B+A+=0。

（2）因为A+=（A*A）+A*，所以A+B=（A*A）+A*B，从而A+B=0⇔A*B=0。

定理4设A∈Cn×n，则下列命题等价：

（1）AA*=A*A；

（2）AA*A+=A+AA*；

（3）A（AA*A+）+=（AA*A+）+A。

证明先证（1）⇔（2）。由引理3式（7）得

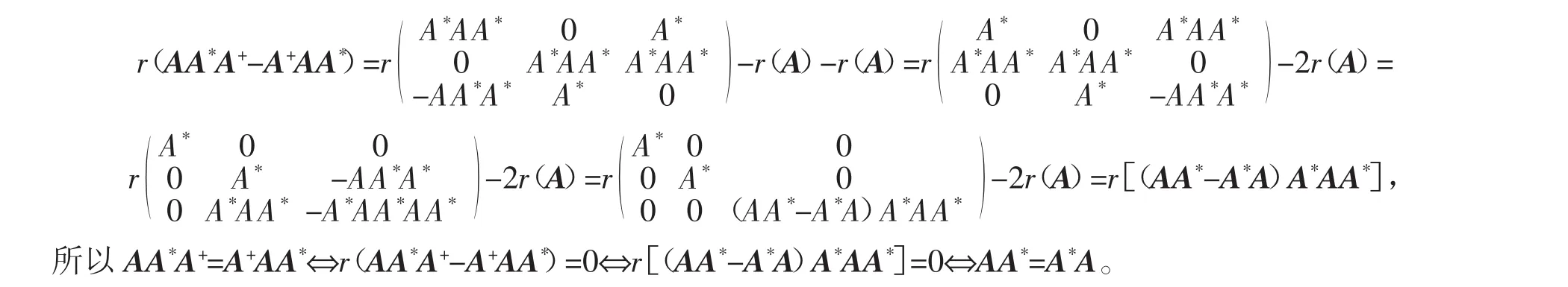
再证（1）⇔（3）。设M=AA*A，由引理3式（7）得

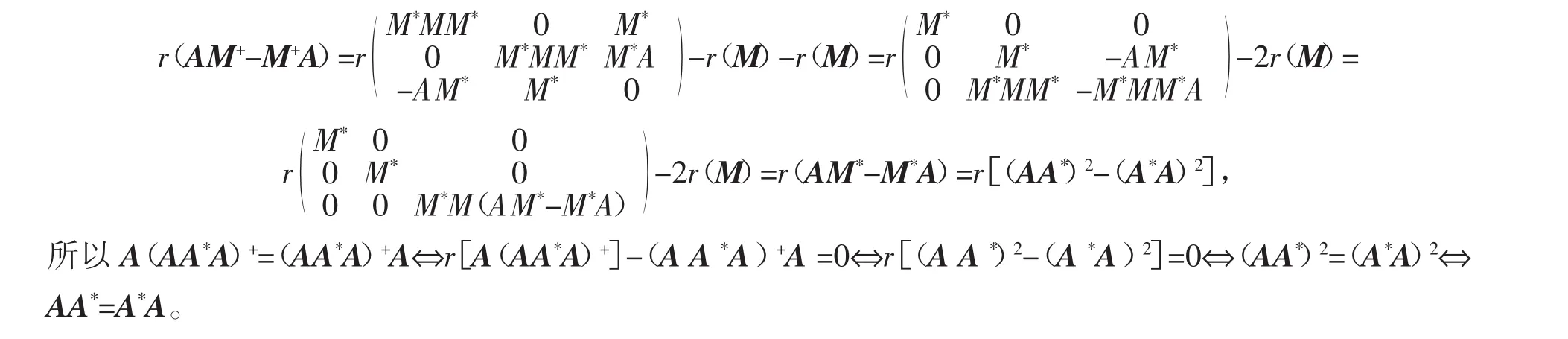
［1］TIAN Yongge.Mixed-type reverse order law for products of three operators［J］.Linear Algebra and its Applications,2011,435: 2658-2673.

［2］CHEN Shizheng,TIAN Yongge.Two sets of new characterizations for normal and EP matrices［J］.Linear Algebra and its Applications,2003,375:181-195.

［3］MARSAGLIA G,STYAN G P H.Equalities and inequalities for ranks of matrices［J］.Linear and Multilinear Algebra,1974,2: 269-292.

［4］TIAN Yongge.Using rank formulas to characterize equalities for Moore- Penrose inverses of matrix products［J］.Applied Mathematics and Computation,2004,147:581-600.

［5］CAMPBELL S L,MEYER C D.Generalized Inverses of Linear Transformations［M］.New York:Dover Publ.Inc.,1991.

［6］黄旭,刘丁酉.Moore-penrose逆交换性的秩方法［J］.湖北民族学院学报:自然科学版,2010（2）:124-126.

【责任编辑：王桂珍foshanwgzh@163.com】

M atrix rank method in the application of generalized inverse

HUANG Xu

（The Public and Basic Teaching and Research Center,Zhuhai College of Jilin University,Zhuhai519041,China）

While the matrix rank method,as a specific approach,can find the unique route in most cases, simplifying the complex,this method plays an important role in matrix theory.This paper introduces the matrix rank method in the application of generalized inverse.

generalized inverse matrix;the matrix rank method;Schur complement

O151.21

A

1008-0171（2015）05-0021-03

2014-12-15

黄旭（1985-），男，湖北天门人，吉林大学珠海学院助教。