基于EEMD方法的爆破振动信号去噪研究

张树标，王　柳，饶运章，饶　睿

（1.赣州有色冶金研究所，江西 赣州 341000；2.江西理工大学 资源与环境工程学院，江西 赣州 341000）

基于EEMD方法的爆破振动信号去噪研究

张树标1，王柳1，饶运章2，饶睿1

（1.赣州有色冶金研究所，江西 赣州 341000；2.江西理工大学 资源与环境工程学院，江西 赣州 341000）

鉴于小波类去噪法存在小波基和分解层数的选择问题、EMD类去噪法受限于端点震荡和模态混叠效应，将EEMD方法引入，对爆破振动原始信号进行去噪研究。在EEMD分解的基础上，通过波形和频谱分析，得到IMF4~ IMF8属于爆破振动真实信号分量，将其重构，获取了爆破振动真实波形。与EMD去噪法相比，EEMD去噪法避免了端点震荡和模态混叠效应的影响，不仅有效去除了噪声，还保留了爆破真实波形的真实性和完整性。

爆破振动信号；EMD；EEMD；去噪

0　引言

爆破振动信号依靠测振仪实现数字化转变和记录[1]。然而，受监测环境和仪器本身制造误差影响，爆破振动原始信号不可避免地携带噪声，精度受限[2-4]。因此，如何在多频率叠加的原始信号中提取真实爆破振动信号是后续分析的前提和基础。

在爆破振动信号去噪领域，先后出现了小波（包）类[5]和EMD（EmpiricalMode Decomposition）类[6]去噪方法。众所周知，小波（包）方法存在小波基和分解尺度的选择问题[7]；EMD是一种自适应分解方法，但分解过程易受异常事件干扰，产生端点震荡和模态混叠效应，去噪效果受限[8]。针对EMD的弊端，Wu Z.等人[9]提出利用白噪声均匀分布的特性，将其混入原始信号中，平滑异常事件，使信号具备均匀分解尺度的信号新分解方法—集成经验模式分解（Ensemble Empirical Mode Decomposition，EEMD）方法。为此，将EEMD方法引入，对爆破振动原始信号进行去噪研究。

本文在EEMD分解的基础上，采用EEMD方法进行去噪研究，选取某钨矿山的井下采场崩矿爆破实测信号，进行MATLAB实例仿真，保留了爆破振动波的真实性和完整性，为后续分析提供了基础，为同类矿山爆破去噪研究提供借鉴参考价值。

1　EEMD原理

EEMD方法是在EMD方法的基础上发展的，基本原理相似，与EMD方法相比，EEMD方法只是在分解前借助白噪声对原始信号中的异常事件进行了平滑，其基本步骤有[10-11]：

步骤一：原始信号为S（t）（t=1，2，…，n，为时间采样点数），将白噪声加入S（t）中，平滑异常事件，得到信号Si（t）（i表示加入噪声的次数），并设定IMF分量的判断条件：（1）极点数和零点数差值不超过1；（2）上、下包络线以时间轴为准，局部对称，也即均值为0。

步骤二：确定Si（t）所有极值点，通过三次样条插值获取Si（t）的上包络线Smax（t）和下包络线Smin（t），并求取上、下包络线的均值曲线m（t）：

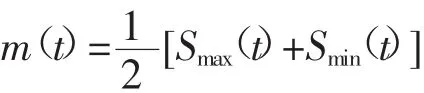
将m（t）从Si（t）中输出，则剩余值h1（t）为：

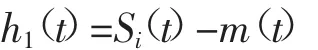
步骤三：如果h1（t）符合IMF分量判断条件，将其作为第一个IMF分量输出，否则代替Si（t）重复筛选过程，直至k（k=1，2…n）次迭代后，剩余值hk（t）成为一个IMF，即IMFi，1（t）=hk（t）。

将IMFi，1（t）输出后，第一阶段的剩余信号Ri，1（t）为：

步骤四：对Ri，1（t）继续重复步骤二、步骤三的筛选工作，从高频到低频依次输出IMFi，2（t）、IMFi，3（t）…、IMFi，j（t），直至最后的残差：

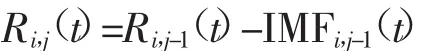
当Ri，j（t）再也无法分解出新的IMF分量时，终止筛选工作。那么信号Si（t）为IMFi，1（t）、IMFi，2（t）、IMFi，3（t）、…、IMFi，j（t）及余量Ri，j（t）之和：

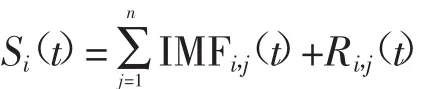
由于加入的i次噪声是不相关随机序列，其统计均值为零，将各IMFi，j（t）分量进行整体平均后，加入的i次噪声将相互抵消。那么，各分量IMFj（t）可转变为：

则原始信号S（t）表示为：

S（t）=IMF1（t）+IMF2（t）+…+IMFj（t）+Rj（t）

2　EEMD方法去噪

EEMD方法是基于幅值的自适应性分解过程，分解结果是依据频率高低依次排列的多个IMF分量和一个余量R，类似滤波器原理，可知[12]：

EEMD高通法去噪：

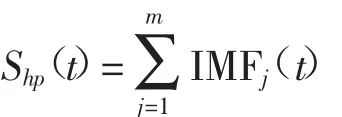
EEMD带通法去噪：

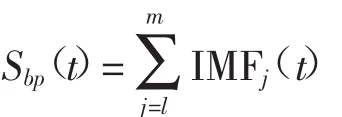
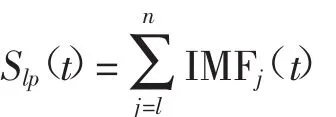
式中：l、m、n为IMF分量的筛选顺序。

研究表明，爆破振动信号频率通常集中在200Hz以下的相对低频区域，由于炸药爆炸产生巨大能量的突然加载，速度幅值大，波形有明显突变现象，能量是瞬时的，波形又迅速衰减；噪声则呈相对高频特性，分散于整个信号，速度幅值小，波形均匀连续、无突变现象。而爆破测振仪的最小记录频率为2 Hz，也即，真实爆破振动波的频率集中在2~200Hz，那么，爆破振动原始信号经EEMD分解后，选择带通法去噪，便可提取真实爆破振动波信号。

EEMD低通法去噪：

3　MATLAB实例仿真

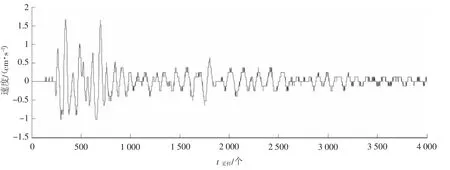
图1　爆破振动实测波形Fig.1　Blasting vibrationm easured waveform

选取某钨矿山井下采场崩矿爆破实测信号（见图1）进行EEMD去噪研究，。由于该矿地下水丰富，节理裂隙发育，且爆源至监测点中间存在断层F3，爆破振动原始信号携带了大量噪声，部分波形呈类方波，而非类正弦波，尖点也模糊不清，为提取真实爆破振动信号，需进行去噪处理。

3.1信号分解和分析

为分离和识别噪声与真实爆破振动信号，对原始信号进行EMD与EEMD分解，提取IMF分量信息，见图2和图3，并对各分量作Fourier变换，求取频谱，见图4和图5。经EMD和EEMD分解，原始信号均获取了10个IMF分量和一个余量R，且各分量按照频率高低依次排列。其中，IMF1~IMF3波形均匀分布、频率大，是噪声分量[13]，但受异常事件干扰，EMD分解存在端点震荡（图2实线箭头所指）和模态混叠（图2虚线箭头所指）现象，必然影响后续分析，而EEMD分解借助噪声对异常事件进行平滑，不存在端点震荡和模态混叠现象；IMF4~IMF8波形明显，其对应的频率幅值大，是爆破振动真实信号分量[14]；IMF9、IMF10和余量R频率均小于2Hz，可视作是干扰信息[15]。

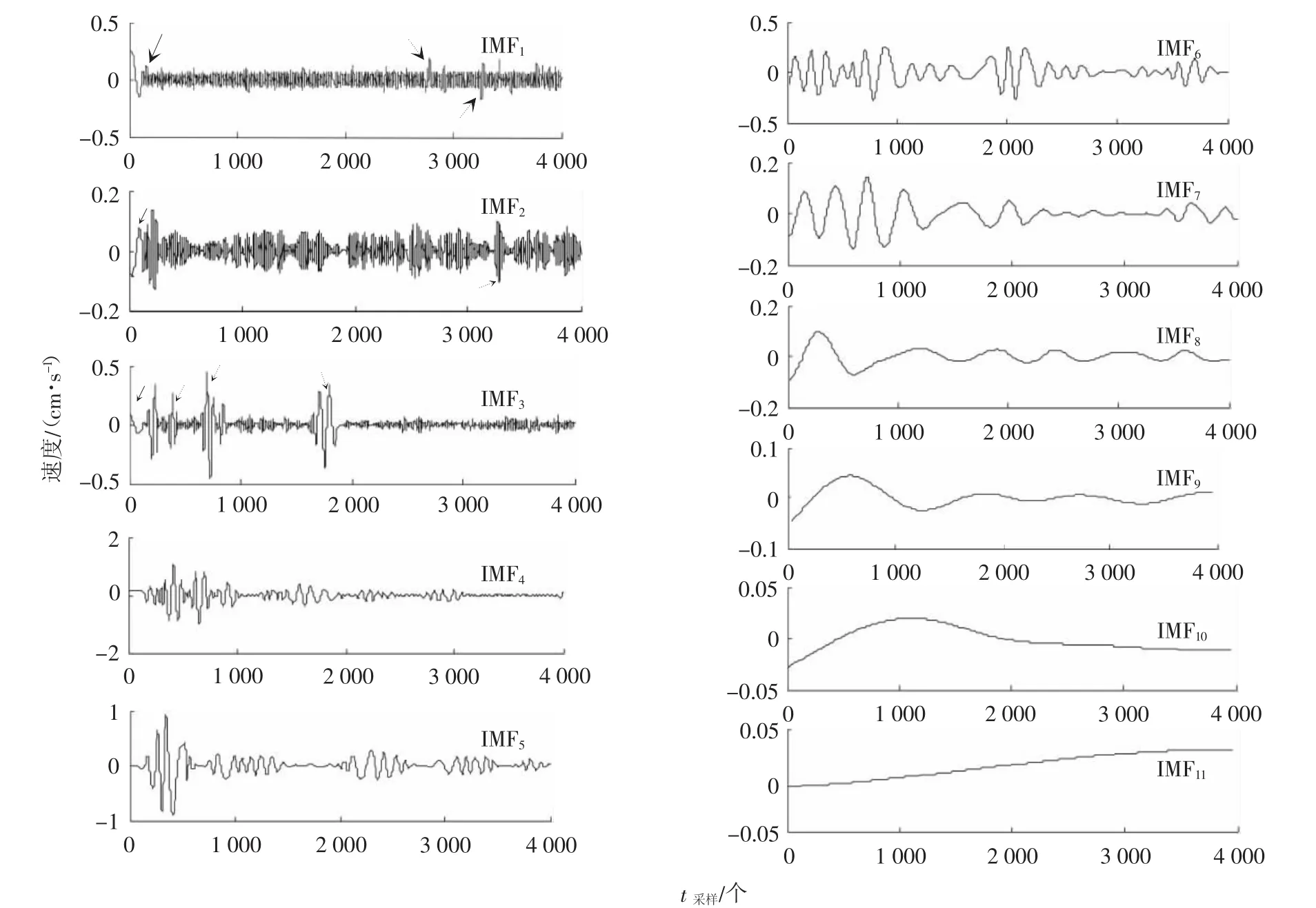
图2　EMD分解Fig.2　EMD decom position

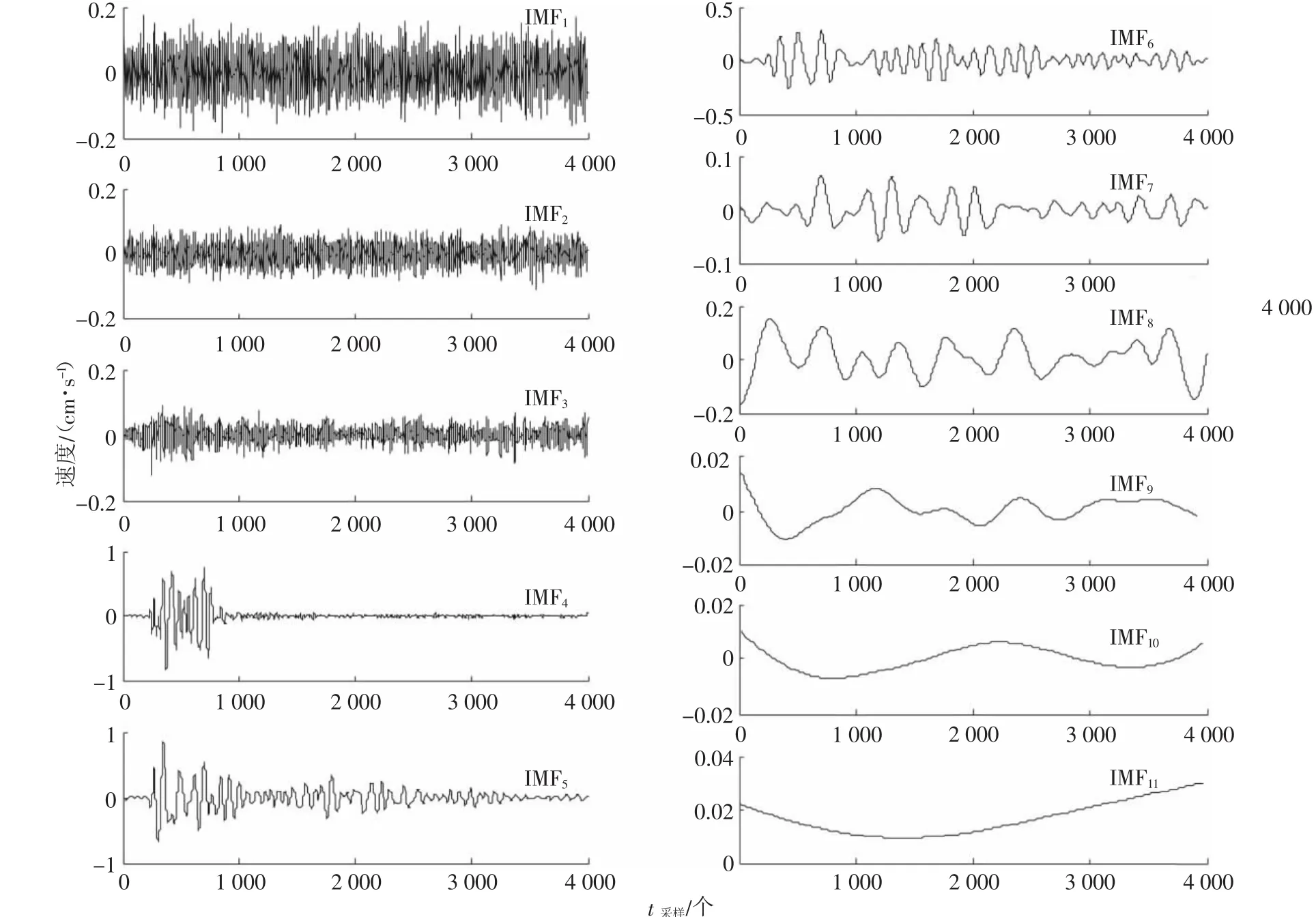
图3　EEMD分解Fig.3　EEMD decom position

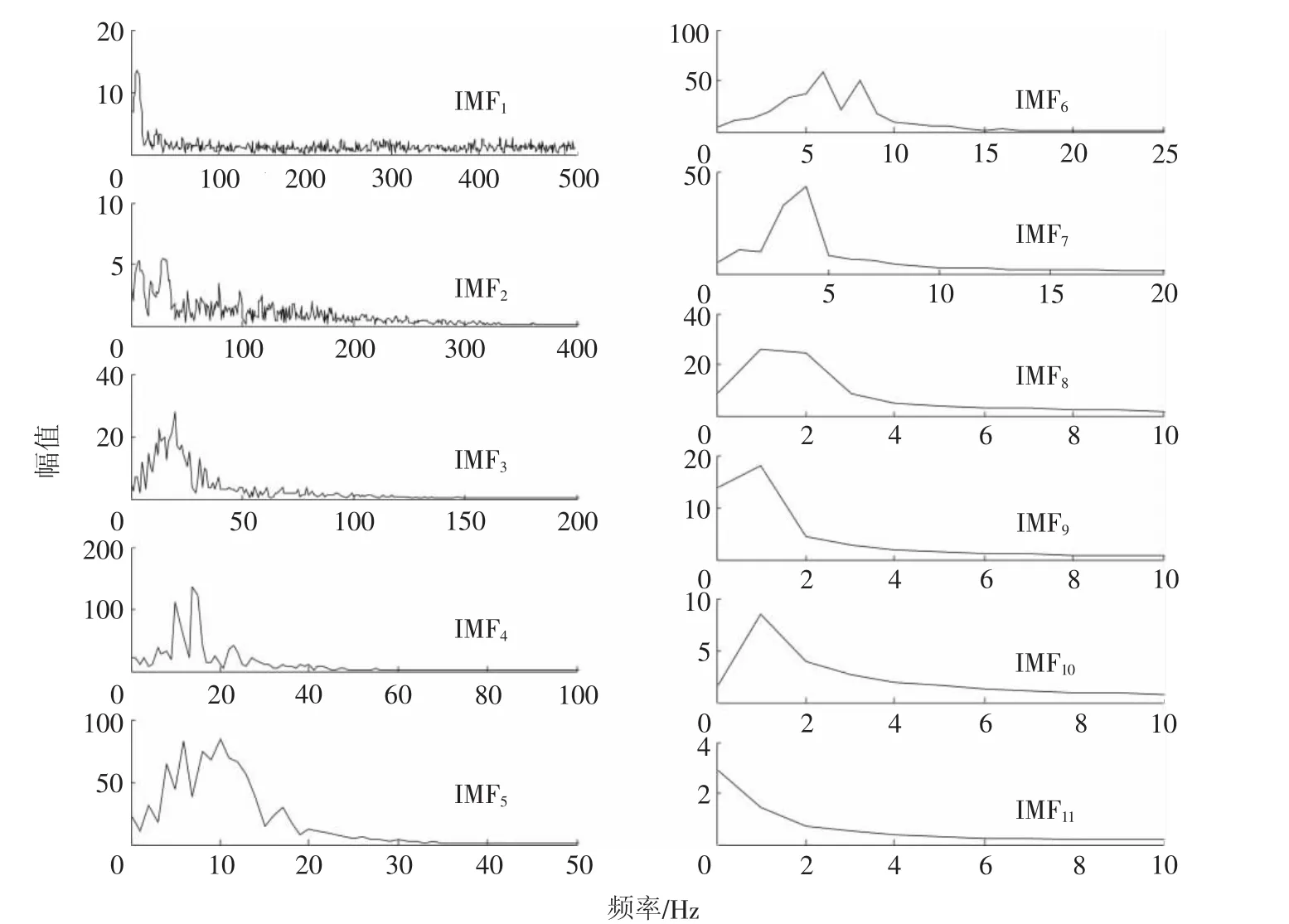
图4　IMF（EMD分解）分量频谱Fig.4　IMF（EMD decom position）com ponentsspectrum

图5　IMF（EEMD分解）分量频谱Fig.5　IMF（EEMD decom position）com ponentsspectrum

3.2信号去噪

上述分析可知，IMF4~IMF8是属于爆破振动真实信号的分量，那么，选择带通法对原始信号进行去噪，也即，重构IMF4~IMF8分量，舍弃其余分量，便可提取爆破振动真实信号，见图6。可知，经EMD和EEMD带通去噪后，爆破振动波清晰可见，噪声被有效去除。但受EMD分解产生的端点震荡和模态混叠现象影响，在EMD带通法去噪过程中，部分混叠在噪声中的真实波形被舍弃，爆破振动波存在端点震荡（图6实线箭头所指）和（图6虚线箭头所指）失真；EEMD分解则借助噪声平滑了爆破振动原始信号中的异常事件，避免了端点震荡和模态混叠现象的发生，如此，EEMD带通法去噪后，不仅噪声被有效去除，而且保留了爆破振动波的真实性和完整性。

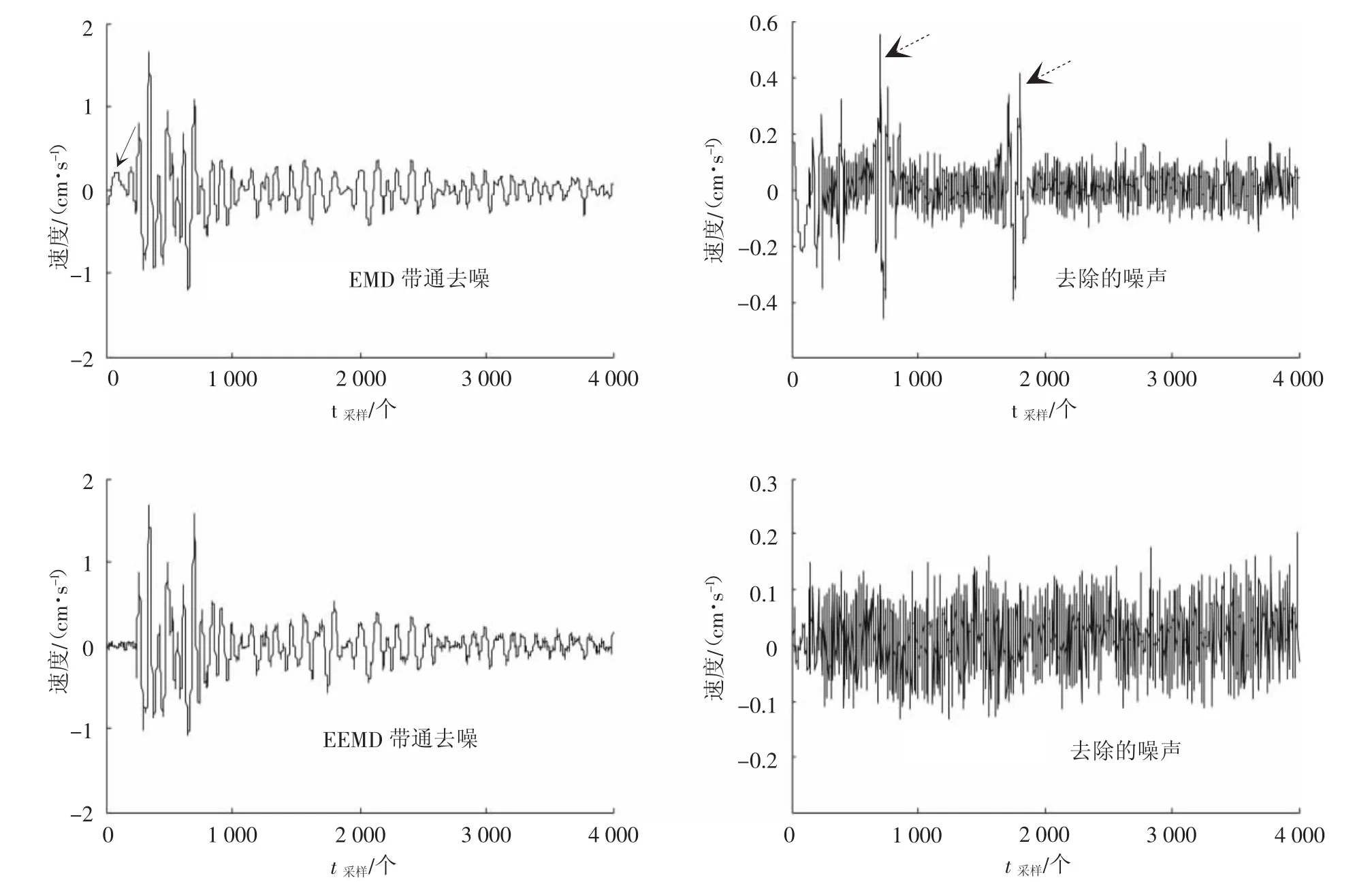
图6　真实信号与噪声Fig.6　True signaland noise

4　结论

基于爆破振动实测信号，借助EMD和EEMD方法，进行了爆破振动波去噪研究，得出以下结论：

（1）EMD和EEMD分解具有自适应性，将爆破振动原始信号分解成若干个按照频率高低的IMF分量，实现了噪声与真实信号的分离，为去噪提供了基础。

（2）经波形识别和频率分析，IMF4~IMF8分量是属于爆破振动真实信号分量，舍弃剩余分量，将IMF4~IMF8分量重构，提取了爆破振动真实波形。

（3）受EMD分解产生的端点震荡和模态混叠现象影响，EMD带通法去噪后，爆破振动波存在端点震荡和失真；EEMD分解则借助噪声平滑了爆破振动原始信号中的异常事件，避免了端点震荡和模态混叠现象的发生，EEMD带通法去噪后，不仅有效去除了噪声，还保留了爆破振动波的真实性和完整性，为后续分析提供了基础，同时也为声发射、微震、边坡在线检测等信号的提取提供了借鉴。

[1]曾志林.爆破振动对高陡边坡稳定性影响及控制技术研究[D].长沙：中南大学，2010.

[2]中国生.基于小波变换爆破震动分析的应用基础研究[D].长沙：中南大学，2006．

[3] 中国生，徐国元，赵建平.基于小波变换爆破震动阈值去噪的应用研究[J].岩土工程学报，2005，27（9）：1055-1059. ZHONG Guo-sheng，XU Guo-yuan，ZHAO Jian-ping.Study and application of threshold de-noising in seismic signals of blasting based on wavelet transform[J].Chinese Journal of Geotechnical Engineering，2005，27（9）：1055-1059.

[4]饶运章，王柳，饶睿，等.基于EMD与小波阈值的爆破震动信号去噪方法 [J].福州大学学报：自然科学版，2015，43（2）：271-276. RAO Yun-zhang，WANG Liu，RAO Rui，et al.A method for blasting vibration signal denoising based on empircal mode decomposition and wavelet threshold[J].Journal of Fuzhou University：NaturalScience Edition，2015，43（2）：271-276.

[5]夏晨曦，杨军，李顺波，等.最优小波包基算法在爆破振动信号去噪中的应用[J].爆破，2011，28（3）：4-7. XIA Chen-xi，YANG Jun，LIShun-bo，et al.Application of Best Wavelet Packet Basis Algorithmin De-noising of Blasting Vibration Signal[J].Blasting，2011，28（3）：4-7.

[6]饶运章，王柳，邵亚建.基于EEMD的爆破震动能量安全分析[J].科技导报，2015，33（4）：61-65. RAO Yun-zhang，WANG Liu，SHAO Ya-jian.Safety analysis of EEMD-based blasting vibration energy[J].Scienceand Technology Review，2015，33（4）：61-65.

[7]孙新建，李成业.岩石爆破震动信号分析的EEMD滤波方法研究[J].水利水电技术，2013，44（1）：101-104.SUN Xin-jian，LICheng-ye.Study on EEMD filteringmethod for analysison rock blasting vibration signal[J].Water Resourcesand Hydropower Engineering，2013，44（1）：101-104.

[8]赵明生，梁开水，罗元方，等.EEMD在爆破振动信号去噪中的应用[J].爆破，2011，38（2）：17-20. ZHAO Ming-sheng，LIANG Kai-shui，LUO Yuan-fang，et al. Application of EEMD in Blasting Vibration Signal De-noising[J]. Blasting，2011，38（2）：17-20.

[9]WU ZH，HUANGN E.Ensembleempiricalmode decomposition：a noise assisted data analysismethod[J].Advances in Adaptive Data Analysis，2009，1（1）：1-41.

[10]HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decompositionandthehilbert spectrumfor nonlinear and nonstationary time series analysis[J].Proceedings of the Royal Societyof London A，1998，454：903-995.

[11]张义平.爆破震动信号的HHT分析与应用研究[D].长沙：中南大学，2006.

[12]王婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨：哈尔滨工程大学，2010.

[13]唐进元，陈维涛，陈思雨，等.一种新的小波阈值函数及其在振动信号去噪分析中的应用[J].振动与冲击，2009，28（7）：118-121. TANG Jin-yuan，CHENWei-tao，CHEN Si-yu，et al.Waveletbased vibration signal denoising with a new adaptive threshold function[J].JournalofVibrationand Shock，2009，28（7）：118-121.

[14]李夕兵，张义平，左宇军，等.岩石爆破振动信号的EMD滤波与消噪[J].中南大学学报：自然科学版，2006，37（1）：150-154. LIXi-bing，ZHANG Yi-ping，ZUOYu-jun，etal.Filtering and denoisingof rock blasting vibration signalwith EMD[J].Journalof Central South University of Technology：Science and Technology，2006，37（1）：150-154.

[15]李宝山，张义平，王税睿.基于HHT方法在英坪矿II号坑的爆破振动分析[J].工程爆破，2010，16（2）：6-9. LI Bao-shan，ZHANG Yi-ping，WANG Shui-rui.Blasting vibration analysis based on HHT method of the No.2 pit in Yingpingcoalminearea[J].EngineeringBlasting，2010，16（2）：6-9.

De-noising Technology for Blasting Vibration Signal Based on EEMD M ethod

ZHANGShu-biao1,WANG Liu1,RAOYun-zhang2,RAORui1

(1.Ganzhou NonferrousMetallurgy Research Institute,Ganzhou 341000,Jiangxi,China;2.SchoolofResourceand EnvironmentalEngineering，Jiangxi universityofScienceand Technology,Ganzhou 341000,Jiangxi,China)

EEMDmethod was introduced for the de-noising ofblasting vibration signal,for the disadvantagesof the two traditional de-noisingmethods,namely,choice ofwavelet basis and decomposition level for thewaveletbased de-noisingmethod,endpoint shock and modal aliasing effects for EMD class de-noising.On the basis of EEMD decomposition,waveform and spectrum analysis determined that IMF4~IMF8 were components of real blasting vibration signal.Real blasting vibration wavewere obtained by reconstructing IMF4~IMF8 components.Compared with EMD de-noisingmethod,EEMD De-noisingmethod avoid the effects of the endpoint shock andmodemixing by effectively removing thenoiseand retaining theblastwaveof realauthenticity and integrity.

blasting vibration signal;EMD;EEMD;de-noising

10.3969/j.issn.1009－0622.2015.04.003

TD235.3

A

2015-05-29

国家自然科学基金项目（51364010）

张树标（1964-），男，江西进贤人，高级工程师，主要从事采矿工艺和地压控制研究工作。

饶运章（1963－），男，江西会昌人，博士，教授，博导，本刊编委，主要从事采矿工程、爆破工程和环境岩土工程方面的教学科研工作。