基于局部和非局部空间信息的图像分割算法

沈 灏

(中北大学 电子测试技术国家重点实验室，山西 太原 030051)

图像分割是将图像中有意义的特征或区域提取出来的过程，是图像理解和计算机视觉中的关键技术［1-2］。现阶段已提出许多图像分割的方法，其中以聚类为基础的图像分割算法得到广泛应用。最常用的聚类方法是FCM。传统的硬聚类HCM 或K－均值聚类算法［4］可以准确表示图像的每个区域或像素属于的类。但这种算法不能有效地对图像的重叠区域进行分割。Lingras［4］最早将粗糙集理论引入到聚类算法中，提出了粗糙C 均值聚类算法RCM。该算法将确定属于某类的对象放到该类的下近似中，而将可能属于某类的对象放到该类的上近似中。但是这些算法在划分聚类的时候需要人为选取阈值。阴影集概念的提出，得到了处理含有不确定区域和模糊区域图像的新方法，并将其应用于RCM算法中。将阴影集概念与模糊聚类算法相结合，提出了SCM算法［5］。

为了提高SCM 算法对噪声的处理，考虑局部信息，提出了结合局部空间信息的SCM 图像分割算法克服了现有图像分割方法对噪声的灵敏度问题。然而当图像中的噪声较高时，一个像素的邻域像素中可能还会包含异常的特征。对于这样的图像，结合局部空间信息可能仍无法产生令人满意的分割结果。最后提出了结合局部和非局部空间信息的阴影集均值聚类图像分割算法，得到了较好的分割结果。实验结果显示，该算法明显优于传统算法。

1 传统的FCM 算法

FCM 算法最早由Dunn 提出［2］。传统的模糊C 均值聚类(FCM)目标函数:

Jm为各样本与其聚类原型的加权误差平方和，C 为聚类数，n 为像素个数，μik为隶属度，m 为加权指数，dik表示第i类中的样本与第i 类的聚类原型vi之间的失真度，欧几里得距离:

目标函数满足如下限制条件:

聚类准则是取目标函数的极小值，根据拉格朗日数乘法，得到使Jm(U，V)为最小值的μik和vi如下:

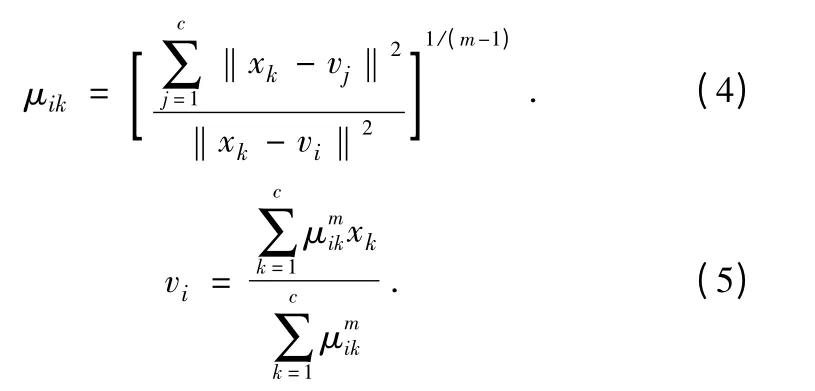
2 SCM 算法

SCM 是由阴影集的概念产生，定义在模糊集的基础上。阴影集中，相应的模糊集被划分为3 个层次，分别为隶属度为0 的对象集合，隶属度为1 的对象集合和隶属度为0 到1之间的对象集合。阴影集定义为:

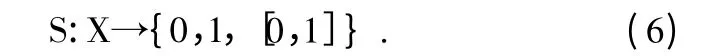
这里的S 是论域，包括区域中的所有像素，阴影集由S(x)=［0，1］的所有像素组成，图1 说明了一个模糊集(顶部)和它相应的阴影集。在阴影集处理中，隶属度为1 的对象集合称为核(core)，隶属度为0 的对象称为负域(exclusion)，隶属度位于0 和1 之间的对象集称为阴影集(shadow)，阴影集中的对象隶属度都定义在(0，1)区间，而不再用单个确定的隶属度值来刻画，相比于模糊集，阴影集的处理更为简单。模糊集的阴影化处理中，通过一个阈值λ 将模糊集隶属度分成三部分，隶属度小于λ 的对象，将其隶属度设定为0;而对于隶属度大于1－λ 的对象，将其隶属度设定为1 或模糊集的最大隶属度值。在这样的处理中，参数λ 的选取最重要，其选取应该维持原模糊集整体的不确定性。

图1 阴影集的划分

优化目标函数定义如下:

相应地，定义核、阴影和负域如下:

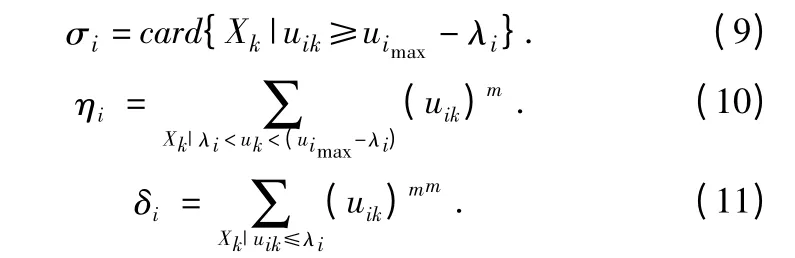
离散的情况下，若表示对象属于某个集合的隶属度值，优化目标(8)能够转化为:

uimin和uimax分别表示模糊集隶属度最小和最大值。设第i 个类的聚类中心为Vi，对象xi属于第i 个类的隶属度为uij，则聚类中心定义如下:

其中，m ＞1 是模糊系数，λI是相应的阈值。

P 和q 是控制隶属度值的重要关系参数。总的来说，SCM 算法的执行过程类似于模糊C－均值聚类算法，算法描述:

1)初始化聚类中心

Vi，i=1;…;C。模糊化系数m，最大迭代次数tmax，t=1。

2)重复步骤3 至步骤5，增加t 的值，直到t ＞tmax。

3)根据(3)式计算隶属度uik。

4)根据(7)式计算阈值λi。

5)根据(13)式更新聚类中心Vi。

3 基于局部和非局部空间信息的阴影集模糊聚类分割算法

传统的SCM 图像分割算法存在明显缺点。问题在于没有充分利用图像的空间信息，而是直接将图像中像素点集作为数据点进行聚类，通常导致图像中含有噪声的像素错误的分类。然而，当图像中的噪声水平高时，所分析的一个像素周围邻域的其他像素也可能含有不正常的点。提出将非局部空间信息加入SCM 聚类算法中。非局部空间均值算法由Buades et al.首次提出［3］。找到相似邻域像素集合，通过对这些像素加权平均进行降噪处理，基于同样的原理得到非局部空间信息的SCM 算法(NLSCM)。与基于局部空间信息的SCM 算法比较，像素之间的聚类中心距离的测量受到非局部信息的影响dnl通过图像中所有像素的中心距离的平均加权计算，定义

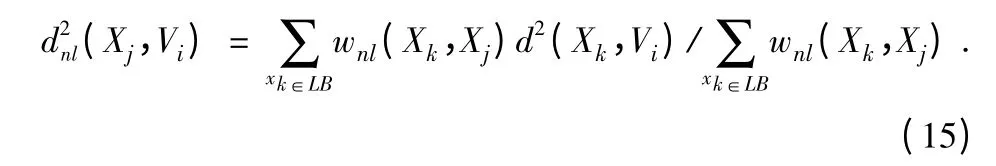
此处wnl是像素xk和xj的相似度。Nk和Nj是固定大小的方形窗口，Nk和Nj的差别通过欧式加权距离‖v(Nk)－v(Nj)‖ρ作为测量标准，其中ρ ＞0 是高斯核的标准偏差。使用高斯加权欧氏距离函数得出更多中心像素周围像素的权重。两个类的像素权重如下:

参数h 是选择程度，它控制指数函数的衰减。

基于图像像素点之间的距离和聚类中心由(15)式子得到，像LSSCM 算法中一样计算、更新聚类中心和隶属度函数。除了LSSCM 算法中的步骤3，其他步骤都是一致的。新算法集成了SCM 算法，局部和非局部空间信息的所有优点。实验结果表明该算法分割效果更好。

4 实验结果

将上述图像分割算法应用于合成图像，分别加入0.15的高斯噪声和0.3 的Rician 噪声。分别用FCM 算法、SCM算法、SFCM 算法、LSSCM 算法、NLSSCM 算法和LNLSSCM算法对含噪图像进行分割，结果如图2，图3 所示。

定义分割精确度指标如下:

对应于上图的分割精确度指标如下，表1 和表2 分别是加入0.15 高斯噪声和接入0.3 的Rician 噪声的合成图像的精确度指标。

表1 加入不同高斯噪声后的分割精度指标

图2 加入0.15 的高斯噪声后经不同算法的分割结果

图3 加入0.3 的高斯噪声后经不同算法的分割结果

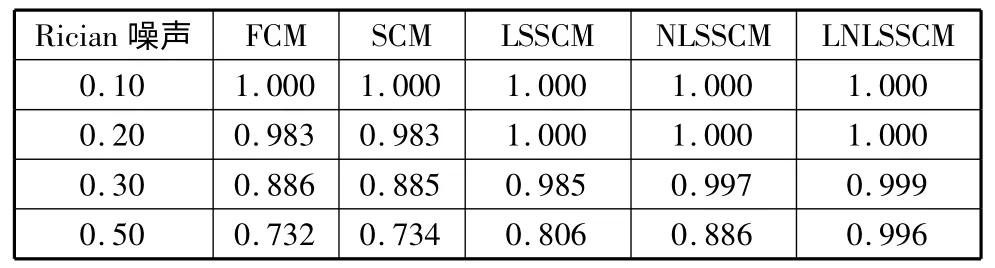
表2 加入不同Rician 噪声后的分割精度指标

5 结论

该算法在SCM 算法的基础上进行改进，结合局部和非局部空间信息，通过比较调试分析，结果，明显看出该算法在抑制噪声方面取得了良好的分割效果。实验证明，本文所提出算法的设计思想切实可行且分割效果明显。

［1］Buades A，Coll B，Morel J－M.A non－local algorithm for image denoising［G］.In CVPR，2005.

［2］Balafar M A.Fuzzy c－mean based brain MRI segmentation algorithms［J］.Springer Science+Business Media B.V，2014(41):40－349.

［3］Buades A，Coll B，Morel J－M.On image denoising methods［G］.Technical Report 2004－15，CMLA，2004.

［4］Pedrycz W，Fernando G.An introduction to fuzzy sets:analysis and design［M］.Cambridge，MA:MIT Press，1998.

［5］Wang X，Wang Y，Wang L.Improving fuzzy c－ means clustering based on feature－ weight learning.Pattern Recogn Lett，25:90－130.