基于径向基网络动态称量数据修正

仝 宇

(太原理工大学信息工程学院，山西 太原 030024)

基于车辆经过高速公路称重区时有不稳定因素，双台面动态汽车辆称重衡［1］逐步取代单台面称重。本文应用建立在非参数回归基础上的广义神经网络GRNN 对原始称重信号做预处理，在大样本条件下拟合称重过程信号，拟合时间极短。其结果传入RBF 网络作为输入神经元之一。为此，文章根据实际情况对货车车型做出具体定义，与其他影响因子并入RBF 神经网络输入。在多元网络输入影响下，进一步修正动态称重运算值。在处理器中利用径向基GRNN－RBF 结合进行信号拟合逼近，有效地提高称量精度和速度。

1 双台面动态称量信号分析

汽车动态称重衡双秤台面由两个秤台、四路传感器组成。如图1，1、2 只传感器为一组，接收到的信号称为一路信号;3、4 只传感器为第二组，接收到的信号称为二路信号;以此类推。

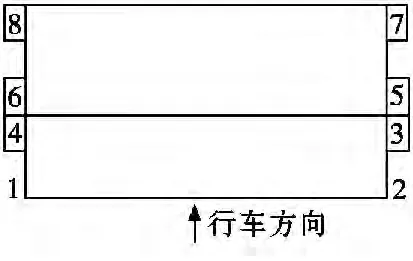
图1 车辆动态称重衡双秤台面

车辆上秤后，前、后秤台传感器开始采集重量信号，形成离散曲线，针对于单路传感器而言，车辆有几个轴采样曲线就会形成几个波峰。

本文将在不同车型、不同速度下进行动态称重信号的曲线逼近以及数据处理。速度在30 km/h 以内，研究的车型主要有2、3、4、5、6 轴车中包含的不同轴型车。

图2 为车辆轴型示意图，本文分析的不同车型，是基于车辆不同的轴型。在实验数据中要以车型为一个输入神经元，因而在此做简单介绍。

两轴型车:12 轴型车:车辆前轴+后轴为轴组代码图中1 +2。三轴型车:车辆前轴+中轴+后轴为轴组代码图中1 +2 +2，称之为15 轴型车。以此类推。

实验依据山西某地区测试车型，共包含:两轴型车代码:12 型;三轴型车:13、14、15 型;五轴型车:1125 型、155 型、119 型、129 型。

图2 车辆轴组代码图

2 基于GRNN 网络称重信号预处理

2.1 GRNN 算法依据

广义神经网络建立在非参数估计回归的基础上，以样本数据为后验条件，执行Parzen 非参估计，依据最大概率原则计算网络输出。

假设x、y 是两个随机变量，其联合概率密度为f(x，y)，若已知x 的观测值为x0，y 相对x 的回归为:

y(x0)即在输入为x0的条件下，y 的预测输出。应用Parzen 非参数估计，可由样本数据集{xi，yi}ni=1，按下式估算密度函数f(x0，y):

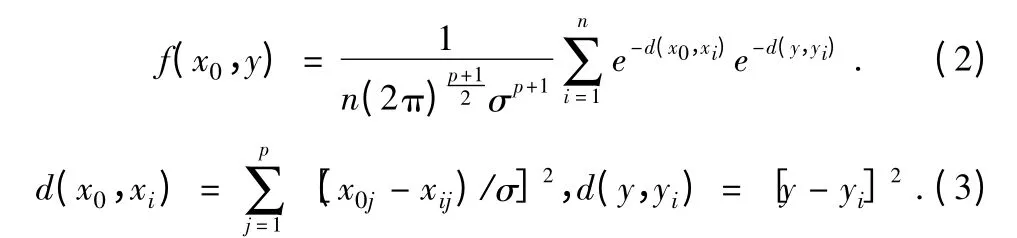
式中，n 为样本容量，p 为随机变量x 的维数。σ 称为光滑因子，实际上就是高斯函数的标准差。将上式代入，并交换积分与求和的顺序，有:

上式中，分子为所有训练样本算得的yi值的加权和，权值为e－d(x0，xi)。GRNN 对所有隐含层神经元的基函数采用相同的光滑因子。

2.2 GRNN 称重系统建模及仿真

网络模型由输入层、隐含层、加和层和输出层构成。

1)输入层接收样本的输入，即双台面上各时刻采样点重量采样值，写成S* R 矩阵，形式为［x1，x2，…，xn］，对于过衡货车，每轴重量采样点n 多达千个以上。隐含节点中心直接选择所有的网络输入转置形式的R* Q 矩阵，即［x1，x2，…，xn］'。

2)计算每一个输入到每一个中心的欧几里德距离，作为隐含层的输入。

在Matlab 中，使用dist(pos)函数，pos 是一个S* Q 矩阵，函数计算向量之间的距离，返回一个对称矩阵，其主对角线元素为0，表示向量与其本身的欧式距离为零。

3)隐含层径向基函数选择高斯函数。算法是:

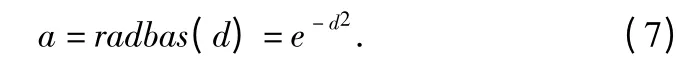
函数包含对S* Q 矩阵计算径向基的结果。

4)光滑因子的设定σ 采用缺一交叉验证方法。

其中m∧(－i)σ(xi)是略去第i 个数据点后得到的函数估计。

5)加和层的神经元分为两种，第一种神经元计算隐含层各神经元的代数和，称为分母单元;第二种神经元计算隐含层神经元的加权和，称为分子单元，输出层将加和层的分子单元、分母单元的输出相除，即得y 的估算值。

图3 为单路传感器双轴12 轴型车辆称重拟合前后对比图，通过交叉验证的处理方法取光滑因子σ=5。仿真收敛时间为0.121 049 seconds.

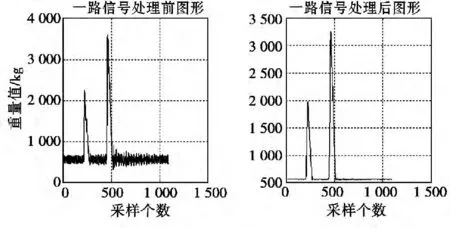
图3 车辆单路传感器拟合前后称重信号波形图

广义神经网络建立在非参数回归的基础上，经向基层采取dist 计算加权输入，用netprod 计算网络输入，传输函数为radbas.第二层为现行层，用normprod 计算加权输入，用netsum 计算网络输入。拟合之后的重量值进行均值求和算法得到称重计算值，作为RBF 神经网络的输入神经元之一。

3 基于RBF 网络称量数据修正

3.1 改进的RBF 网络建模

径向基函数指某种沿径向对称的标量函数，通常定义为空间中任一点X 到某一中心Xi之间欧氏距离的单调函数。

RBF 网络是一种三层前馈神经网络，输入层由感知单元组成，将网络与外界环境连接起来;隐层是非线性的，在输入空间到隐层空间之间进行非线性变换;输出层是线性的，对输入层的训练数据做出响应。设输入层、隐层、输出层的节点数分别为N，M，S，输入输出样本(X，Y)，其中分别为N 维和S 维向量。

隐层节点的激活函数φ(X)=φ(‖X－Xi‖)，i=1，2…M;Xi是基函数的中心，‖●‖是距离测度，该网络也取欧几里德函数。RBF 网络技术就是要寻求一个插值曲面(即函数F)通过所有的有效数据点。

用矩阵形式表示为:F(X)=φ(r)* W，W 为隐含层输出权值。

RBF 网络就是利用径向基函数生成的函数空间来逼近某个非线性函数。径向基函数同样取Gussion 分布函数:

3.1.1 确定网络输入输出

实验中将单轴过衡速度、GRNN 拟合后称重均值、称重波形峰值、上秤斜率、下秤斜率、车型代码等信号特征值作为网络输入。表达为1* N 的矩阵形式:

网络的输出是货车匀速过衡称重测量值，作为网络约定真实值。

3.1.2 确定径向基函数中心

为减少隐含层神经元数量，降低结果不稳定、减少总迭代次数，采用改进的K－means 聚类算法设定样本中心。

1)从N 个数据对象中采用最大距离法选取k 个初始簇中心k0i;

2)首次迭代中，对每个簇样本求其到k 个各中心的距离，将该样本归到距离最短的中心所在的簇。一般采用簇内误差平方和作为标准测度函数。

定义簇内标准测度函数为:

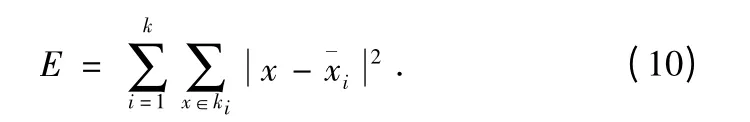
式中，ki表是第i 个数据对象簇，xi为该簇数据平均值，也为簇集的中心。

3)计算新的簇集中心与初始簇中心x0i的差值。设置聚类阈值ε，当该差值大于ε 时，将此刻聚类中心赋值于x0i。重复步骤2)，重新给新的簇集中心分配样本数据，并计算新的簇集中心xi。重复步骤3)，直到差值小于ε 时结束迭代。

聚类阈值公式为:

若满足上式则结束迭代步骤，表示簇内误差平方和已收敛，此时簇内成员不再发生变化，聚类结束。

3.1.3 基于OLS 算法确定隐含层权值

1)设定隐含层节点数I，通过K－means 算法确定各节点中心;

2)根据输入样本，得出由高斯函数计算得到的回归矩阵P;

3)将P 进行正交三角分解:P=UA .

4)根据矩阵U、向量d 计算g，根据Aw=g，求出权值。

3.2 仿真结果

实验中选取岢岚高速190 组称重测量数据，均分为五组进行仿真。每次实验选取前38 组输入数据及静态称重数据作为训练样本设计径向基输入网络，用第一组建立好的网络去测试之后38 组数据，预测效果急剧变差。如图4。

图4 time=0.281 672 seconds

加入第二组完成训练的数据。以此类推，直到将五组实验数据都曾被设置为测试样本为止。

图5 time=0.259 052 seconds

图6 time=0.161 854 seconds

图7 time=0.133 785 seconds

图中十字代表网络估计值，虚线代表约定真实值。从中得出结论:随着测试样本数据的增加，称量重量误差逐渐减小。双台面地磅距离LED 显示屏一般10 m 左右，假设货车达到过衡最大时速30 km/h，则称重显示时间约为1.2 s。加入其它时间差后，实验训练时间完全满足高速入口称重时间，有效解决称重堵塞问题。误差小于2%，达到国家标准。如表1 为第五组修正后的称重误差。

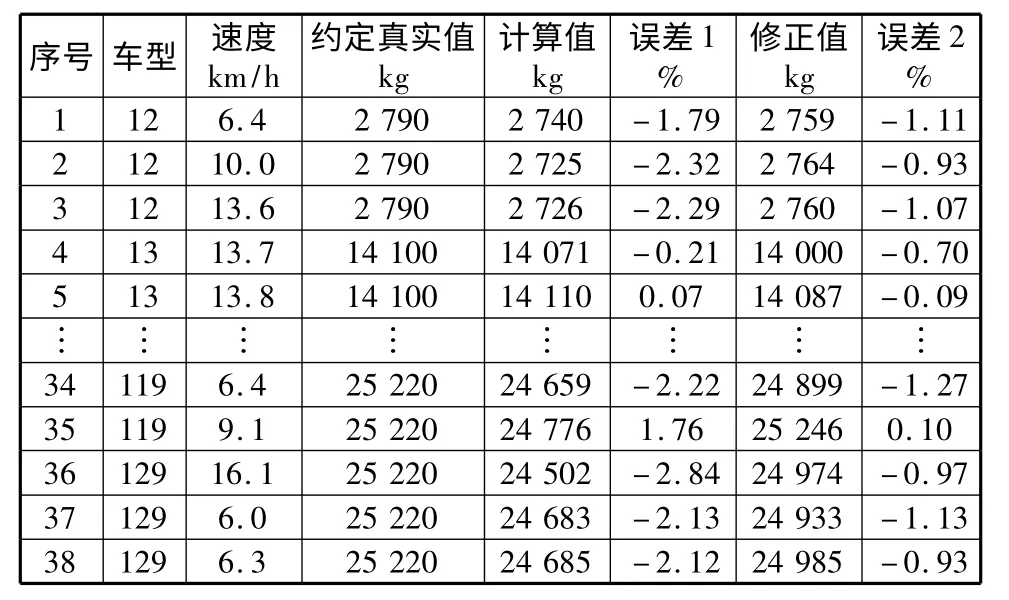
表1 第五组修正后的称重误差

4 结论

实验中首次将GRNN 与RBF 算法结合应用于双台面动态衡，对高速路口动态车辆重量采集信号进行拟合回归。运算得到的重量值将成为RBF 网络的输入参数之一。应用径向基函数对称重信号进行非线性函数逼近，样本逐渐增大，非线性逼近效果渐好，训练时间极短。继续增大，GRNN 与RFB 结合处理在非线性拟合回归、逼近性能上的优势会更佳明显，称重时间上更优于其他神经网络，适用于高速公路计重称量。

［1］Moses F.Weigh-in-motion System Using Instrumented Bridges［J］.Transportation Engineering Journal，1979，105(3):233－249.

［2］中国国家标准化管理委员会.GB/T 21296－2007.动态公路车辆自动衡器［S］.北京:中国标准出版社，2008－09－01.

［3］吴有庆.双秤台超限检测控制系统及其应用［J］.衡器，2006(1):6.

［4］胡春海，陈静.用于动态称重的模型参数估计方法［J］.自动化与仪表，2005，20(4):23－25.

［5］郑惠群，陈偕雄.动态称重技术问题的分析与研究［J］.科技通报，2006，22(4):567－570.

［6］张瑞，吕文红，张瑞玺.基于神经网络自适应滤波的车辆动态称重系统研究［J］.公路交通科技，2010，27(7):138－141.