悬浮条件下声阵列定位技术研究
2015-11-28庞龙飞徐建军李世中
庞龙飞,徐建军,李世中
(中北大学机电工程学院,山西 太原 030051)
随着现代战争的发展,武装探测系统不但在微波、红外和激光探测三个传统领域得到很大发展,也在寻求新的途径和新技术。声阵列探测定位技术是以独特的优势而得到国内外的重视,在雷达、军用、航天等方面有着广泛的应用[1]。自上世纪80 年代以来,声阵列定位技术得到迅速发展。美国BBN 系统和技术公司开发的“枪弹定位器”声测系统,通过测量弹丸飞行中的声激波特性来探测弹丸并进行分类,可探测到90%的射击,定位精度为方位小于2°,水平3°。进入90 年代以来,我国也开始着手研制声阵列等探测武器系统,由中国电子科技集团制造的新型反狙击手声探测仪,也逐渐配备到实战中[2]。
本文主要对平面四元十字阵的定位精度和性能进行研究,根据该阵型的定位算法,统一采用误差合成理论,对由时延引起的平面四元十字阵的方位角、距离精度进行具有一般意义的推导,在此基础上,利用Matlab 软件对该阵型的定位性能进行仿真。
1 被动声定位技术的原理
被动声定位是利用声敏感元件将接收到的声信号转换成电信号,经过放大电路处理后,将信号以电流或电压形式输出,然后经过处理得到目标的位置信息,其中声传感器的质量和性能将直接影响到系统的精度[3]。其机理是将声传感器在空中布置成一定的几何形状的阵列,用以接受声源目标的信息,通过检测声到达各个传感器的不同延时来计算出目标的方位距离。
在被动声定位的算法中常用到阵列,阵列的作用是提供一个延时信号,用来提取目标的位置信息。定位阵列主要有线阵、平面四元阵以及立体阵列。假设一个阵列由N 个声传感器阵元组成,可以得到N-1 个相互独立的时延,而空中的目标可以简化成点目标,所以有三个自由度,因此四个阵元组成的声传感阵列可以满足要求。由于定位系统悬浮于空中,目标为低空或超低空飞行直升机,并且考虑到十字阵的分维特性和冗余较小,所以选取平面四元阵来进行研究[4]。
2 声阵列方程推导及精度分析
平面四元十字阵结构原理如图1 所示,四个传感器坐标为S1(l/2,0,0),S2(0,l/2,0),S3(-l/2,0,0),S4(0,-l/2,0),其中l 为十字阵对角线的距离。设目标声源的直角坐标为Q(a,b,c),球面坐标(r,φ,θ)。
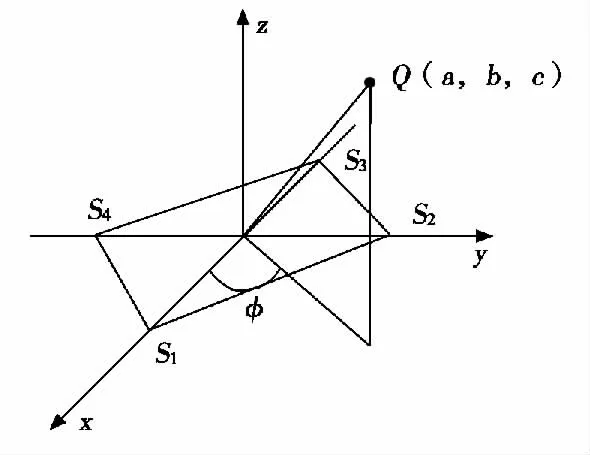
图1 空间定位原理图
假设目标为点声源Q,目标产生的声源以球面波形势传播,声源到达阵元S1的传播时间为t1,相对于S1声源到达S2、S3、S4的时延为τ1、τ2、τ3。目标到达原点距离r,方位角φ(0≤φ≤90),俯仰角θ(0≤θ≤90),与时延τ1、τ2、τ3以及阵元间距的关系可得出:

式中,d21为声信号到S2与S1的声程差;d31为声信号到S3与S1的声程差;d41为声信号到S4与S1的声程差。
通过求解以上方程可得:
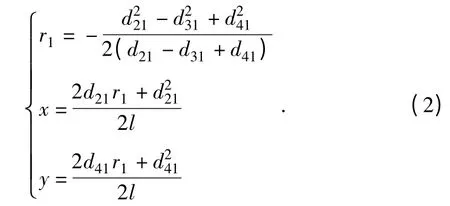
由于r》l,r1≈r,所以可近似得:
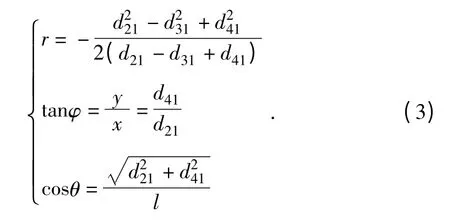
由以上式子可以看出,只要测得平面十字阵所得到的三个相对延时值,就可以得到目标的位置距离信息。
3 声阵列定位精度仿真
3.1 距离估计精度仿真
图2 是定距精度与方位角关系图,其中方位角取60°,距离300 m,阵元间距取0.35 m,声速取340 m/s。图中四条从上到下曲线分别代表时延为10,15,35,50 时的结果,下同。
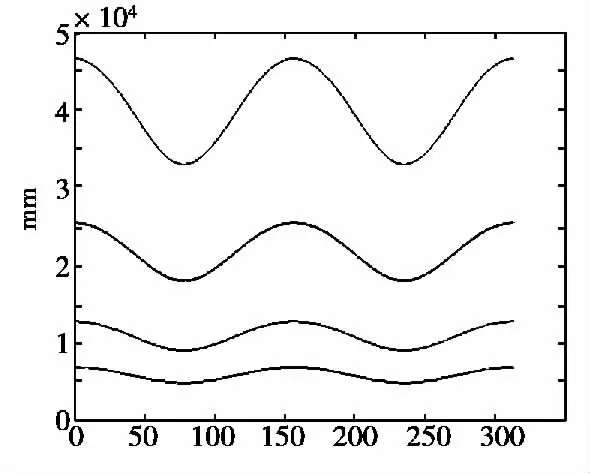
图2 定距精度与方位角的关系
由图2 可以看出,方位角距离误差的影响就较小,在方位角为n×180°时,定距误差达到最大值,但定距误差随方位角变化的变化还是很小,仍可以认为定距精度受方位角影响较小。
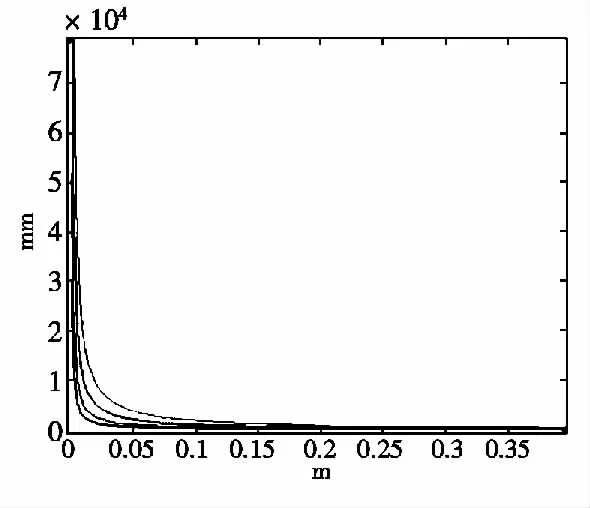
图3 定距精度与阵元间距的关系
由图3 可以看出,阵元间距对定距精度的影响较大,定距精度随着阵元间距的增大而越精确,当阵元间距增大到一定程度后,定距精度将没有明显的变化。考虑到声阵列的小阵元间距趋势,以及设备的灵活性和便携性,应该选取合适的阵元间距,并不是越大越好。
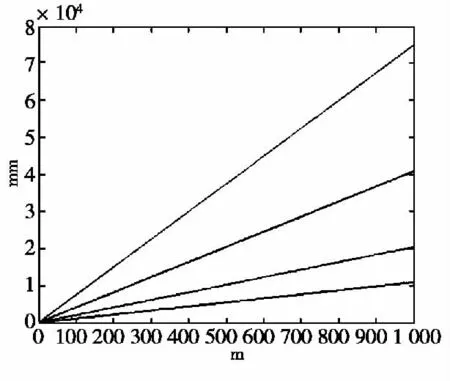
图4 定距精度与目标距离的关系图
由图4 可以看出,定距精度与目标距离呈线性正比关系,因为探测目标主要是低于200 m 的低空目标,可以看到,此时定距误差10 m 以内,定距精度基本可以满足要求。
3.2 方位角估计精度仿真
图5 方位角误差随方位角改变而变化的曲线图,由图可以看出,方位角基本对方位角误差没有影响,但根据公式推导和原理,当方位角为nπ 时,方位角误差处于最大状态,但方位角误差是随方位角的改变而改变幅度很小,所以认为方位角的变化对方位角误差没有影响。
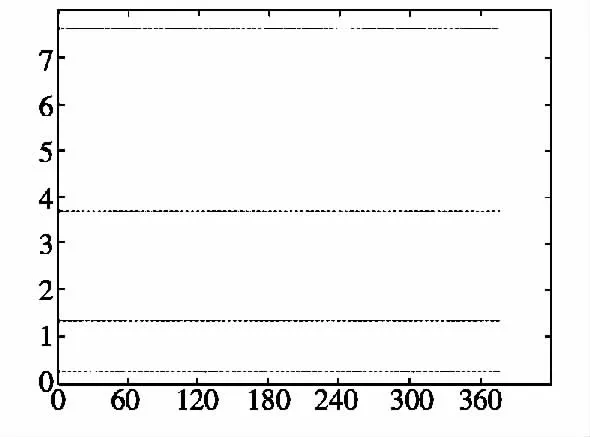
图5 方位角误差与方位角关系
图6 是方位角误差与阵元间距关系图,方位角误差随阵元间距的增大而减小,当阵元间距超过0.25 m 时,方位角误差没有明显的变化。

图6 方位角误差与阵元间距关系
4 结论
本文主要介绍了平面四元十字形声阵列定位原理,并对拟采用的四元阵列的定位算法进行了推导,为了能够在理论上论证其定位性能,结合误差分析公式对该阵型的定位精度做了理论分析,并对分析结果进行了Matlab 仿真,分别从定距误差与方位角的影响、定距误差与阵元间距的影响、定距误差与目标距离的影响、方位角误差与方位角的影响、方位角误差与阵元间距的影响共五个方面进行分析,仿真结果在理论上证明了采用该阵列在悬浮条件下进行定位的可行性。
[1]陈华伟.低空目标声测被动定向技术研究[D].西安:西北工业大学,2002:18-21.
[2]王燕妮.被动声探测定位技术研究[D].太原:中北大学,2006:38-41.
[3]向瑾.基于四元十字阵的被动声定位技术研究[D].太原:中北大学,2008.
[4]殷恒刚.基于小波变换二次相关时延估计算法的声定位技术及试验研究[D].南京:南京理工大学,2009:20-21.
