Nudging同化方案改进及其在西北太平洋海域M2分潮模拟中的应用＊

魏泽勋，王永刚，高秀敏，方国洪

（1.国家海洋局 第一海洋研究所，山东 青岛266061；2.青岛海洋科学与技术国家实验室 区域海洋动力学与数值模拟功能实验室，山东 青岛266071）

潮汐是海洋最基本的运动形式之一。它与人类活动关系密切，准确掌握潮汐的运动规律对渔业生产和生态环境都具有重要意义。此外，航运交通、海港工程、海岸防护、能源利用、环境保护以及军事活动等，都受潮汐现象的影响。潮汐学的研究还对其他方面如海洋污染物扩散、泥沙运动、水体交换、风暴潮等问题的研究有重要作用。因此，针对潮汐进行研究具有重要的理论意义和实际应用价值。

对于中国近海，早期的潮汐研究主要是基于观测资料［1－2］，这些观测资料大多集中于沿岸和岛屿附近。随着计算技术的发展，数值模拟方法逐渐被普遍应用于潮汐研究［3－16］，这些研究大多集中于中国近海的某一海区，或者将渤、黄、东海作为一个整体。

近年来，观测资料尤其是卫星高度计资料的大量涌现，使潮汐学研究有了更多、更全面的资料［17－22］。如何更有效率地利用这些资料，是摆在人们面前的重要问题。多年来，人们尝试将观测资料与数值模型相结合，从而使数值模拟结果与观测尽可能接近，这种将观测资料与数值模型相结合的方法称为资料同化方法。早在上世纪70年代，方国洪［23］就成功建立了潮波变分同化模式，并用于模拟黄海M2分潮。随后将同化方法用于潮波模拟的研究多集中在2000年以后。韩桂军等［24－25］采用基于最优控制理论的伴随法建立伴随模型，利用验潮站的水位资料以及TOPEX／Poseidon（以下简称T／P）卫星测高数据在黄海、东海进行变分数据同化试验，优化了开边界条件，提高了数值模拟的精度。吕咸青和方国洪［26－27］采用伴随法，由渤海沿岸19个验潮站的潮汐调和常数来反演渤海海域的开边界条件，数值模拟结果较好地体现了渤海M1和M2潮波的基本特征。吴自库等［28］利用伴随同化方法，把T／P卫星高度计资料提取得到的沿轨分潮调和常数同化到二维非线性潮汐数值模式中去，通过优化模型中的开边界条件和底摩擦系数，较好地模拟了南海M1和M2分潮的潮汐。张继才和吕咸青［29－30］探讨了独立底摩擦系数如何选取，才能使得渤、黄、东海M2分潮伴随同化数值模拟的精度提高。丘仲锋等［31］将大约10a的T／P高度计资料，利用伴随同化方法，同化到二维非线性潮汐数值模式中，模拟了黄海、渤海区域M2，S2，O1和K1分潮。Zu等［32］通过将T／P卫星高度计资料同化到正压潮波模型中，模拟了南海8个主要分潮（M2，S2，K1，O1，N2，K2，P1和Q1）。以上都是变分同化方法在潮波模式中的应用，趋近法同化也常用于潮波数值模式中。王永刚等［33］采用趋近法，建立了渤、黄、东海潮汐同化数值模式。丘仲锋和何宜军［34］利用趋近插值法将高度计资料同化到二维非线性潮汐数值模式中，模拟了中国近海M2分潮的分布。朱学明等［35］利用FVCOM海洋数值模式，采用趋近法同化84个沿岸验潮站的观测资料，模拟了西北太平洋海域M2，S2，K1和O1四个主要分潮。

本文基于POM模式，采用Nudging同化技术，建立了西北太平洋海域潮波数值模式，并利用数值实验讨论了Nudging松弛项的差分方案及Nudging松弛系数对潮波模拟结果的影响。

1 数值模式

POM（Princeton Ocean Model）模式是美国普林斯顿大学Blumberg和Mellor自1977年建立起来的，经过多次修改，已成为最常用的海洋数值模式。该模式水平方向采用正交曲线网格，网格配置采用Arakawa C网格，垂向上采用σ坐标。

本文采用Nudging同化方法，同化方案如下：

模式原方程为

式中，ζ为水位；n为时刻；Δt为时间步长；L为连续方程中的其他项。

1）Nudging松弛项显式差分方案

在模式原方程基础上增加Nudging项，则：

式中，ζo，m为第m个观测水位；α为松弛系数，该值愈大表明趋近观测值的约束作用愈强；ωm为其权重，若dl≤DM，ωm＝exp（1－dl／D），若dl＞DM，ωm＝0（其中；D取1／6°；DM取1°；λ和φ分别为经度和纬度）。

进一步得：

2）Nudging松弛项隐式差分方案

在模式原方程基础上增加Nudging项：

最终得：

本文以西北太平洋海域为研究区域，范围为105°30′～141°E、14°～41°N。模式的水平分辨率为1／12°×1／12°（图1），垂向分10层。水深采用ETOPO2（National Geophysical Data Center，NOAA）并利用当地海图资料进行修正。开边界处采用水位开边界条件进行驱动，调和常数由TPXO 6.0［36］资料集插值得到。本研究采用正压潮模拟，温度和盐度均取常数，模式从静止状态开始计算，对M2分潮模拟40个周期，存储最后一个周期结果，并对其进行调和分析，用来研究西北太平洋海域潮汐分布及潮波传播特征。

本文用到的观测值采用218个沿岸和岛屿验潮站资料和218个卫星高度计提取得到的调和常数资料，其站位分布见图2，其中153个沿岸和岛屿验潮站资料和185个卫星高度计提取得到的调和常数资料用在模式中，剩余的用于模拟结果的检验。

图1 计算网格Fig.1 Model grid

图2 观测值站位分布图Fig.2 Locations of observation stations

2 数值实验及结果

针对Nudging松弛项显式和隐式差分方案及Nudging松弛系数对潮波模拟结果的影响，设计了一系列的数值实验（表1），实验1不加Nudging松弛项，实验2～7加Nudging松弛项且采用显式差分方案，实验8～15加Nudging松弛项且采用隐式差分方案。为了分析各试验模拟结果的优劣，本文用振幅绝均差和迟角绝均差来表示计算值和观测值之间的偏差，这种方法比较直观。其计算公式为：

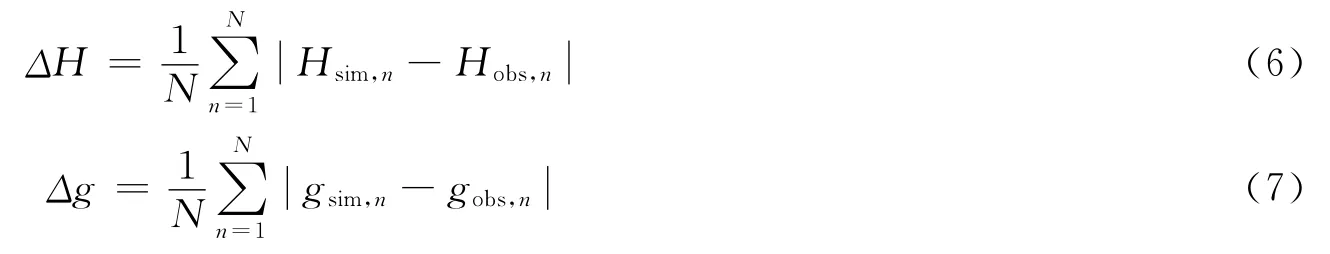
式中，H为振幅；g为迟角；下标sim和obs分别代表计算值和观测值；N为观测值个数。

表1 实验方案设置Table 1 Experiments on nudging schemes

但是我们知道，当振幅较小时，计算和观测的迟角都不太稳定，同时振幅较小时的误差对潮高计算误差影响也较小，故式（7）中不考虑振幅的差别而将所有迟角差进行平均并不十分合理。另一种方法不是很直观，但更合理一些，这种方法取均方根偏差：

式中，a＝Hcosg；b＝Hsing；σ为计算值和观测值之间的距离，它表征了计算值和观测值的偏离程度，而它与观测值变化性的相对偏离程度为相对偏差：

式中，r为线性回归中的相关系数，r2表示计算值和观测值的拟合程度。

表2给出了数值实验模拟结果与98个观测值的偏差对比，从中可以看出：

1）潮波模式中加了Nudging松弛项（实验2～15）的模拟结果要明显优于未加Nudging松弛项（实验1）的模拟结果；

2）在松弛系数取值相等情况下，Nudging松弛项采用隐式差分方案的结果均优于采用显式差分方案的结果；

3）Nudging松弛项差分方案不论为显式还是隐式，模拟结果的偏差都随着松弛系数的增加而逐渐减小，当松弛系数增加到最优值（0.002）后，模拟结果的偏差都随着松弛系数的增加而增加；

4）Nudging松弛项差分方案为显式时，当松弛系数太大时（＞0.005），会导致模式溢出；Nudging松弛项差分方案改为隐式后，能够有效提高松弛系数的阈值。

表2 各实验模拟结果与观测值的偏差对比Table 2 Comparison between numerical simulations and observations

图3给出了实验10模拟得到的M2分潮的同潮图，与Fang等［21］相比，除了在南黄海330°和60°等迟角线走向略有不同外，传播趋势基本相同，较好地体现了西北太平洋海域的潮波传播特征。M2分潮都有4个无潮点，其中2个位于渤海，分别位于黄河口附近和秦皇岛外海；另外2个位于黄海，分别位于成山头附近和海州湾外。最大振幅位于南黄海东部江华湾，接近3m。本文在渤海黄河口附近得到了一个完整的旋转潮波系统，与王永刚等［37］给出的无潮点位置基本一致，而丘仲锋和何宜军［34］以及朱学明等［35］模拟得到的黄河口附近的无潮点基本都已退化到陆地上。

图3 实验10得到的M2分潮同潮图Fig.3 Co－tidal chart of M2from Experiment 10

3 结语

本文基于POM模式，针对Nudging松弛项的差分方案及Nudging松弛系数进行了数值试验，结果表明：

1）引入Nudging松弛项的潮波模拟结果明显优于未加Nudging松弛项的模拟结果；

2）在松弛系数取值相等情况下，Nudging松弛项采用隐式差分方案的结果要优于采用显式差分方案的结果；

3）Nudging松弛项差分方案不论是显式还是隐式，模拟结果的偏差都随着松弛系数的增加而逐渐减小，当松弛系数增加到最优值后，模拟结果的偏差将随着松弛系数的增加而加大；

4）Nudging松弛项差分方案为显式时，当松弛系数太大时，将导致模式溢出；而Nudging松弛项差分方案为隐式时，能够有效增大松弛系数的阈值。

（References）：

［1］WYRTKI K.Physical oceanography of the Southeast Asian waters，Scientific Results of Marine Investigations of the South China Sea and the Gulf of Thailand 1959－1961［J］.NAGA Report，1961，2：195.

［2］FANG G H.Tide and tidal current charts for the marginal seas adjacent to China［J］.Chinese Journal of Oceanology and Limnology，1986，4（1）：1－16.

［3］SHEN Y J.Numerical computation of tides in the East China Sea［J］.Journal of Shandong College of Oceanology，1980，10（3）：26－35.沈育疆.东中国海潮汐数值计算［J］.山东海洋学院学报，1980，10（3）：26－35.

［4］YE A L，ROBINSON I S.Tidal dynamics in the South China Sea［J］.Geophysical Journal of the Royal Astronomical Society，1983，72：691－707.

［5］SHEN Y J，HU D M，MEI L M，et al.Numerical computation of the tides in the South China Sea［J］.Transactions of Oceanology and Limnology，1985，1：1－11.沈育疆，胡定明，梅丽明，等.南海潮汐数值计算［J］.海洋湖沼通报，1985，1：1－11.

［6］FANG G H，YANG J F.A two－dimensional numerical model of the tidal motions in the Bohai Sea［J］.Chinese Journal of Oceanology and Limnology，1985，3（2）：135－152.

［7］DING W L.Distribution of tides and tidal currents in the South China Sea［J］.Oceanologia et Limnologia Sinica，1986，17（6）：468－480.丁文兰.南海潮汐和潮流的分布特征［J］.海洋与湖沼，1986，17（6）：468－480.

［8］DOU Z X，YANG L W，OZER J.Three－dimensional simulation of tidal currents in the Bohai Sea［J］.Acta Oceanologica Sinica，1993，15（5）：1－15.窦振兴，杨连武，OZER J.渤海三维潮流数值模拟［J］.海洋学报，1993，15（5）：1－15.

［9］FANG G H，CAO D M，HUANG Q Z.Numerical simulation on tides and tidal currents in the South China Sea［J］.Acta Oceanologica Sinica，1994，16（4）：1－12.方国洪，曹德明，黄企洲.南海潮汐潮流的数值模拟［J］.海洋学报，1994，16（4）：1－12.

［10］ZHAO B R，FANG G H，CAO D M.Numerical simulation on tides and tidal currents in the Bohai，Yellow and East China Seas［J］.Acta Oceanologica Sinica，1994，16（5）：1－10.赵保仁，方国洪，曹德明.渤、黄、东海潮汐潮流的数值模拟［J］.海洋学报，1994，16（5）：1－10.

［11］ZHANG Z H，WU H D.Numerical computation of tides and tidal currents in the Bohai Sea［J］.Marine Forecasts，1994，11（1）：48－54.张占海，吴辉碇.渤海潮汐和潮流数值计算［J］.海洋预报，1994，11（1）：48－54.

［12］YE A L，MEI L M.Numerical modelling of tidal waves in the Bohai Sea，the Huanghai Sea and the East China Sea［J］.Oceanologia et Limnologia Sinica，1995，26（1）：63－70.叶安乐，梅丽明.渤黄东海潮波数值模拟［J］.海洋与湖沼，1995，26（1）：63－70.

［13］WAN Z W，QIAO F L，YUAN Y L.Three－dimensional numerical modeling of tidal waves in the Bohai，Yellow and East China Seas［J］.Oceanologia et Limnologia Sinica，1998，29（6）：611－616.万振文，乔方利，袁业立.渤、黄、东海三维潮波运动数值模拟［J］.海洋与湖沼，1998，29（6）：611－616.

［14］WANG K，FANG G H，FENG S Z.A 3－D numerical simulation of M2tides and tidal currents in the Bohai Sea，the Huanghai Sea and the East China Sea［J］.Acta Oceanologica Sinica，1999，21（4）：1－13.王凯，方国洪，冯士筰.渤海、黄海、东海 M2潮汐潮流的三维数值模拟［J］.海洋学报，1999，21（4）：1－13.

［15］FANG G H，KWOK Y K，YU K J，et al.Numerical simulation of principal tidal constituents in the South China Sea，Gulf of Tonkin and Gulf of Thailand［J］.Continental Shelf Research，1999，19：845－869.

［16］ZHU X M，BAO X W，SONG D H，et al.Numerical study on the tides and tidal currents in Bohai Sea，Yellow Sea and East China Sea［J］.Oceanologia et Limnologia Sinica，2012，43（6）：1103－1113.朱学明，鲍献文，宋德海，等.渤、黄、东海潮汐、潮流的数值模拟与研究［J］.海洋与湖沼，2012，43（6）：1103－1113.

［17］MAZZEGA P，BERGE M.Ocean tides in the Asian semienclosed seas from TOPEX／POSEIDON［J］.Journal of Geophysical Research，1994，99（C12）：24867－24881.

［18］YANAGI T，TAKAO T，MORIMOTO A.Co－tidal and co－range charts in the South China Sea derived from satellite altimetry data［J］.La Mer，1997，35（3）：85－93.

［19］HU J Y，KAWAMURA H，HONG H S，et al.Tidal features in the China Seas and their adjacent sea areas as derived from TOPEX／POSEIDON altimeter data［J］.Chinese Journal of Oceanology and Limnology，2001，19（4）：293－305.

［20］LIU K X，MA J R，HAN G J，et al.Tidal harmonic analysis of TOPEX／POSEIDON data in North west Pacific by introducing difference－ratio relations［J］.Acta Oceanologica Sinica，2002，24（4）：1－10.刘克修，马继瑞，韩桂军，等.引入差比关系法分析西北太平洋TOPEX／POSEIDON卫星高度计测高数据［J］.海洋学报，2002，24（4）：1－10.

［21］FANG G H，WANG Y G，WEI Z X，et al.Empirical cotidal charts of the Bohai，Yellow，and East China Seas from 10years of TOPEX／Poseidon altimetry［J］.Journal of Geophysical Research，2004，109（C11006），doi：10.1029／2004JC002484.

［22］LI P L，ZUO J C，LI L，et al.Orthogonalized convolution method for analysis of South China Sea tidal data from TOPEX／POSEIDON［J］.Oceanologia et Limnologia Sinica，2002，33（3）：287－295.李培良，左军成，李磊，等.南海 TOPEX／POSEIDON高度计资料的正交响应法潮汐分析［J］.海洋与湖沼，2002，33（3）：287－295.

［23］FANG G H.Finite difference of tidal equations——least square method and its application of simulation on M2tide in the Yellow Sea［J］.Science in China：Series B，1985，28（4）：356－364.方国洪.潮波方程的有限差分——最小二乘方法及其对模拟黄海 M2潮的应用［J］.中国科学：B辑，1985，28（4）：356－364.

［24］HAN G J，HE B R，MA J R，et al.Optimizing open boundary conditions of nonlinear tidal model using adjoint methodⅠ：The establishment of adjoint model and twin－experiment［J］.Acta Oceanologica Sinica，2000，22（6）：27－33.韩桂军，何柏荣，马继瑞，等.利用伴随法优化非线性潮汐模型的开边界条件Ⅰ：伴随方程的建立及“孪生”数值试验［J］.海洋学报，2000，22（6）：27－33.

［25］HAN G J，FANG G H，MA J R，et al.Optimizing open boundary conditions of nonlinear tidal model using adjoint methodⅡ：Assimilation experiment for tide in the Huanghai Sea and the East China Sea［J］.Acta Oceanologica Sinica，2001，23（2）：25－31.韩桂军，方国洪，马继瑞，等.利用伴随法优化非线性潮汐模型的开边界条件Ⅱ：黄海、东海潮汐资料的同化试验［J］.海洋学报，2001，23（2）：25－31.

［26］LÜ X Q，FANG G H.Numerical experiments of the adjoint model for M2tide in the Bohai Sea［J］.Acta Oceanologica Sinica，2002，24（1）：17－24.吕咸青，方国洪.渤海 M2分潮的伴随模式数值试验［J］.海洋学报，2002，24（1）：17－24.

［27］LÜX Q，FANG G H.Inversion of the tides on the open boundary of the Bohai Sea by adjoint method［J］.Oceanologia et Limnologia Sinica，2002，33（2）：113－120.吕咸青，方国洪.渤海开边界潮汐的伴随法反演［J］.海洋与湖沼，2002，33（2）：113－120.

［28］WU Z K，TIAN J W，LÜX Q，et al.A numerical model of tides in the South China Sea by adjoint method［J］.Oceanologia et Limnologia Sinica，2003，34（1）：101－108.吴自库，田纪伟，吕咸青，等.南海潮汐的伴随同化数值模拟［J］.海洋与湖沼，2003，34（1）：101－108.

［29］ZHANG J C，LÜX Q.Inversion of the spacial varying bottom friction coefficient with the adjoint method［J］.Progress in Natural Science，2005，15（9）：1086－1093.张继才，吕咸青.空间分布底摩擦系数的伴随法反演研究［J］.自然科学进展，2005，15（9）：1086－1093.

［30］ZHANG J C，LÜX Q.Inversion of the bottom friction coefficient in 2Dtidal model of the Bohai，the Yellow and East China Seas［J］.Chinese Journal of Computational Mechanics，2007，24（4）：430－435.张继才，吕咸青.渤、黄、东海二维潮汐模式底摩擦系数的反演［J］.计算力学学报，2007，24（4）：430－435.

［31］QIU Z F，HE Y J，LÜX Q.Tidal adjoint assimilation with the TOPEX／Poseidon altimeter data in the Huanghai and Bohai Seas［J］.Acta Oceanologica Sinica，2005，27（4）：10－18.丘仲锋，何宜军，吕咸青.黄海、渤海TOPEX／Poseidon高度计资料潮汐伴随同化［J］.海洋学报，2005，27（4）：10－18.

［32］ZU T T，GAN J P，EROFEEVA S Y.Numerical study of the tide and tidal dynamics in the South China Sea［J］.Deep－Sea Research I，2008，55：137－154.

［33］WANG Y G，FANG G H，CAO D M，et al.Tides of the Bohai，Yellow and East China Seas by assimilating gauging station data into a hydrodynamic model［J］.Advances in Marine Science，2004，22（3）：253－274.王永刚，方国洪，曹德明，等.渤、黄、东海潮汐的一种验潮站资料同化数值模式［J］.海洋科学进展，2004，22（3）：253－274.

［34］QIU Z F，HE Y J.Assimilation of the M2tides in China Seas with TOPEX／POSEIDON data［J］.Oceanologia et Limnologia Sinica，2005，36（4）：376－384.丘仲锋，何宜军.TOPEX／POSEIDON高度计资料用于中国近海 M2分潮的同化反演［J］.海洋与湖沼，2005，36（4）：376－384.

［35］ZHU X M，BAO X W，HUANG B G，et al.An tidal numerical assimilation modeling in northwest Pacific［J］.Acta Oceanologica Sinica，2012，34（2）：1－12.朱学明，鲍献文，黄必桂，等.西北太平洋的一种潮汐数值同化模型［J］.海洋学报，2012，34（2）：1－12.

［36］EGBERT G D，BENNETT A F，FOREMAN M G G.TOPEX／POSEIDON tides estimated using aglobal inverse model［J］.Journal of Geophysical Research，1994，99（C12）：24821－24852.

［37］WANG Y G，WEI Z X，FANG G H，et al.A numerical study on the effect of changes in water depth and coastline on M2tidal component near the Yellow River Estuary［J］.Advances in Marine Science，2014，32（2）：141－147.王永刚，魏泽勋，方国洪，等.黄河口及其邻近海域水深和岸线变化对 M2分潮影响的数值研究［J］.海洋科学进展，2014，32（2）：141－147.