复合材料层合结构层间应力分析

彭惠芬，夏 晔，王 鹏，王 程

（1.东北石油大学机械科学与工程学院，黑龙江大庆 163318；2.大庆油田有限责任公司钻探工程公司，黑龙江大庆 163453）

复合材料是用物理或化学方法将2种或2种以上单一物质复合而成的一种材料，可发挥单一材料各自特性，取长补短［1－3］。目前，复合材料层合结构在航空航天、机械工程、船舶、医学器械等现代高新技术领域中得以开发与广泛应用［4－5］。因此，提高复合材料层合结构使用寿命，提高其承载能力变得尤为重要，减小层间应力，有效防止脱层效应课题引起了许多国内外科技工作者的广泛关注［6－8］。张培新［9］等采用2种建模方法研究了不同多向铺层复合材料层合板层间应力，研究结果表明受拉层板的自由边界存在不容忽视的层间应力；胡伟平［10］等采用傅里叶和勒让德级数作为插值函数构造层间胶层位移场，结果表明该计算方法具有较好的收敛性，为提高复合材料层间应力分析精度提供新的计算方法；文献［11］将断裂理论引入复合材料损伤分析，成功地对复合材料层合板层间断裂韧性和损伤机理进行分析研究；韩振宇［12］等研究了纤维曲线铺设对刚度影响，合理设计了曲线纤维的铺放，为复合材料层合结构合理设计提供了理论指导；LOPES［13］等推导出基于经典层合板理论耦合的、椭圆的、变系数的偏微分平衡方程，对此偏微分方程进行数值求解，计算其面内弹性反应和抗压屈曲载荷。

1 层合结构层间应力理论分析

根据复合材料力学［14］，正交各向异性材料主方向应力－应变关系为

坐标变换后，用x，y，z表示的应力－应变关系为

复合材料层合结构几何方程为

设无体力，且应力不是坐标x的函数时，平衡方程可表示为

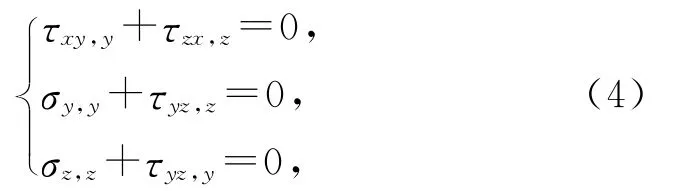
将式（3）代入式（2），最后代入式（4）得：

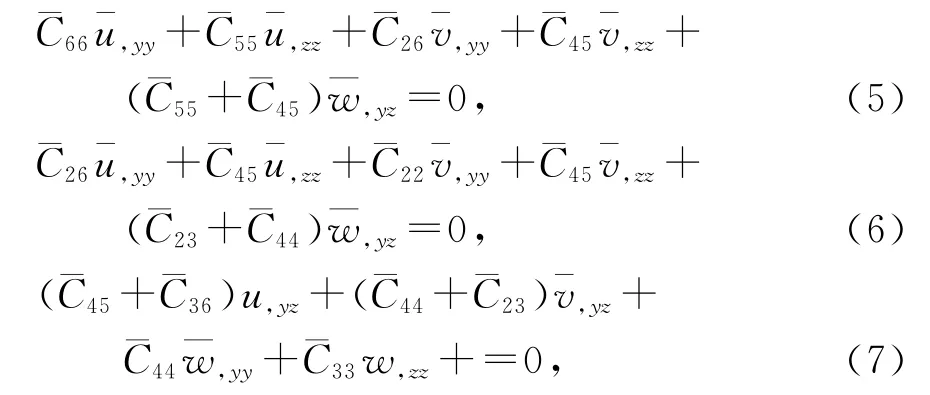
式（5）、式（6）和式（7）没有封闭解，利用力和位移边界条件通过有限差分法求解。即在xoy平面把所求区域划分为若干相同的小正方形格子，每个格子的边长都为h，假设某顶点0上的电位是U0，周围4个顶点的电位分别为u1，u2，u3和u4。将这几个点的电位用泰勒级数展开，当h很小时，忽略四阶以上的高次项，并考虑协调方程联立求解。

2 复合材料层合结构数值模拟

设复合材料层合结构由4 层厚度为t＝0.025 m、长为2m 的正方形单层板复合而成，各层铺设角分别为0°，45°，45°，0°，其几何模型如图1所示，单层板材料性能参数见表1［15］，层合结构上表面受均布载荷P0＝6kPa，分析其层间应力分布规律。

利用ANSYS软件，采用Solid Layered46层单元，根据对称性，取其建立层合板有限元模型。表2为正交铺设层合板层间极值应力理论解与数值解对比结果，从表2中可以看出理论解与数值解吻合较好，最大相对误差不超过8.64%，这说明本文建立数值模型的正确性。

图2、图3分别为0°纤维铺设角复合材料层合板层间x－z方向和y－z方向的应力云图，从图中可以看出层间应力分布情况，其中固定端处层间应力数值最大，x－z方向和y－z方向层间极值应力分别为2.37 MPa和1.82 MPa。

表3列举了不同铺设角下层间极值应力，从表中可以看出对称铺设层合板x－z方向层间应力随着中间层纤维铺设角的增大而减小，y－z方向层间应力随着纤维铺设角的增大而增大，纤维铺设角为（0°／0°／0°／0°）时层间剪应力τxz最大，数值为2.37×106Pa，纤维铺设角为（0°／90°／90°／0°）时 层间剪应力τyz最大，数值为2.01×106Pa。

图1 复合材料层合板结构图Fig.1 Structure diagram of composite laminated structure

表1 复合材料性能参数Tab.1 Material performance parameter of composite laminated structure

表2 不同计算方法结果对比Tab.2 Results comparison with different calculation methods

图2 x－z 方向层间应力Fig.2 Interlaminar stress along x－z direction

图4、图5分别为x－z方向和y－z方向，纤维铺设角为0°／90°／90°／0°时，层合板对角线上各点层间应力随距离变化关系，从图中可以看出：在距o点距离为0～1.348m，层间应力随距离增大变化不大，在距离为1.348～1.418 m，层间应力急剧增大，这表明复合材料层合板边缘为层间应力极值点，易于发生脱层效应。

图3 y－z 方向层间应力Fig.3 Interlaminar stress along y－z direction

表3 不同铺设角下极值剪应力Tab.3 Maximum shear stresses of different ply angles

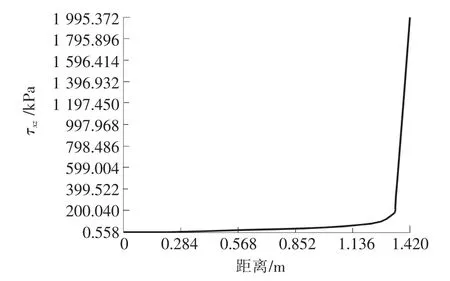
图4 x－z 方向层间应力随距离变化关系Fig.4 Change relation between interlaminar stresses along x－z and distance

图5 y－z 方向层间应力随距离变化关系Fig.5 Change relation between interlaminar stresses along stresses along y－z and distance

3 结 论

1）利用ANSYS软件，建立了复合材料层合板有限元模型，从数值解与理论解比较可以看出：2种方法数据吻合很好，这表明所建数值模型的正确性。

2）分析了不同纤维铺设角下对称层合板层间应力变化规律，分析结果表明：层合板正交铺设时τxz和τyz层间应力数值接近，层间应力相对较小。因此，对称铺设层合结构设计相邻层板采用正交铺设，可有效避免脱层。

3）研究了层合板对角线上各点层间应力随距离变化关系，分析结果表明：层合板内部层间应力数值较小，边缘层间应力数值较大，易于发生脱层效应，因此，结构设计时可在层合板边缘采用加厚黏胶层或边缘带帽等方法抑制脱层。

／References：

［1］ 于艳华，杨国腾.复合材料层间剪切强度测试的研究［J］.测控技术，2012，31（sup）：322－324.YU Yanhua，YANG Guoteng.Research on the test of interlaminator shear properties of composite materials［J］.Measurement ＆Control Technology，2012，31（sup）：322－324.

［2］ 孙志刚，宋迎东，高德平.考虑界面时细观几何结构对复合材料力学性能的影响［J］.材料科学与工程学报，2004，22（4）：488－494.SUN Zhigang，SONG Yingdong，GAO Deping.Influence of micro－structural geometry and interface on composite’s mechanical behavior［J］.Journal of Materials Science and Engineering，2004，22（4）：488－494.

［3］ TANG C A.Numerical simulation of rock failure and associated seismicity［J］.Int J Rock Mech Min Sci，1997，3（4）：249－262.

［4］ MARTIN E，PETERS P W M，LEGUILLON D，et al.Condit ions for matrix crack deflection at an interface in ceramic matrix composites［J］.Materials Science and Engineering，1998，A250：291－302.

［5］ 沈真，杨胜春.碳纤维增强树脂基复合材料力学性能预测［J］.甘肃科技，2012，28（9）：67－69.SHEN Zhen，YANG Shengchun.Forecast of mechanical properties on carbon fiber reinforced resin matrix composite［J］.Gansu Science and Technology，2012，28（9）：67－69.

［6］ 李顺林，肖军.碳纤维增强塑料层合板斜交层间的剪切强度［J］.固体力学学报，1988，9（3）：265－268.LI Shulin，XIAO Jun.The shear strength of angle－interlamination of carbon fiber－reinforced plastic laminates［J］.Chinese Journal of Solid Mechanics，1988，9（3）：265－268.

［7］ 陆金甫，关治.偏微分方程数值解法［M］.北京：清华大学出版社，2004.LU Jinpu，GUAN Zhi.Numerical Solution of Partial Differential Equations［M］.Beijing：Tsinghua University Press，2004.

［8］ ZHAO X L，ZHANG L.State－of－the－art review on FRP strengthened steel structures［J］.Engineering Structures，2007，29（8）：1808－1823.

［9］ 张培新，李亚智.受面内载荷的层压复合材料的层间应力分析［J］.机械强度，2006，28（2）：224－228.ZHANG Peixin，LI Yazhi.Interlaminar stress analysis of composite laminates subjected to pn－plane loading［J］.Journal of Mechanical Strength，2006，28（2）：224－228.

［10］ 胡伟平，孟庆春，张行.受分布载荷复合材料层合板应力分析的一般理论［J］.复合材料学报，2003，20（4）：58－62.HU Weiping，MENG Qingchun，ZHANG Xing.General theory on stress analysis of laminated composite plate pressed by distributed loading［J］.Acta Materiae Composite Sinica，2003，20（4）：58－62.

［11］ ALMUHAMMADI K，ALFANO M.Analysis of interlaminar fracture toughness and damage mechanisms in composite laminates reinforced with sprayed multi－walled carbonnanotubes［J］.Materials and Design，2014，53：921－927.

［12］ 韩振宇，孟庆鑫，路华，等.新型纤维铺放头的方案设计与实验研究［J］.玻璃钢／复合材料，2007（3）：45－47.HAN Zhenyu，MENG Qingxin，LU Hua，et al.Schematic design and expermentalresearch of a new fiber placement head［J］.Fiber Reinforced Plastics／Composites，2007（3）：45－47.

［13］ LOPES C S，CAMANHO P P，GÜRDAL Z，et al.Progressive failure analysis of tow－placed，variable－stiffness composite panels［J］.International Journal of Solids and Structures，2007，44（25）：8493－8516.

［14］ 沈观林，胡更开，刘彬.复合材料力学［M］.北京：清华大学出版社，2013.SHEN Guanlin， HU Gengkai，LIU Bin. Mechanics of Composite Materials［M］.Beijing： Tsinghua University Press，2013.

［15］ 张朝晖.ANSYS11.0结构分析工程应用实例解析［M］.北京：机械工业出版社，2008.ZHANG Zhaohui.Example Analysis of Structural Analysis and Engineering Application of ANSYS11.0［M］.Beijing：Machinery Industry Press，2008.