粘结层厚度对叠层压电振子的影响分析*

王 锐，王玉山，龚立娇34

（1 石河子大学理学院，新疆石河子 832003；2 石河子大学水利建筑工程学院， 新疆石河子 832003；3 石河子大学机械电气工程学院，新疆石河子 832003）

随着低功耗电子产品的出现，供能问题成为急需解决的热门研究问题，研究发现从环境中直接获取能量、供能是一种很好的解决方法；而通常情况下,环境中的能量很有限且常见振源的频率较低，因此对利用环境振动能进行发电并对外供能的研究较多[1-5]；压电陶瓷具有独特的机一电耦合特性，利用压电陶瓷的正压电效应将环境周围的振动能转化为电能的压电式振动发电技术为此提供了一种有效的解决途径，但如何有效地提高压电振动发电装置的安全性和发电能力是需要解决的关键问题。研究发现在外载荷一定，结构尺寸限定的情况下，悬臂支撑方式产生的挠度最大，谐振频率最低[6]。故当前压电式振动发电技术广泛采用悬臂梁压电振子，由于压电陶瓷塑性较差，通常将其粘结在金属基底上构成叠层压电振子，但悬臂梁叠层压电振子在弯曲变形时应变分布不均匀[7]，使压电材料没有得到充分利用，转化效率低；此外，压电振子在制造过程中，压电陶瓷与金属之间粘结层的缺陷也是导致制造失败的一个主要原因[8-9]，可见，粘结层在叠层压电振子中起着至关重要的作用。故为了提高有限体积压电振子的机电能量转换效率及发电能力，本文研究了悬臂梁叠层压电振子在考虑粘结层后的发电能力、频响特性以及粘结层的抗剪性能。

1 叠层压电悬臂梁结构发电原理

由于压电陶瓷硬而脆，通常将其粘结在金属基底上构成压电振子，根据粘结方式的不同，压电振子结构可分为单晶和双晶压电梁，在提高压电振子发电量方面，实验表明，双晶压电悬臂梁结构的发电能力都大于单晶压电悬臂梁结构[6]，故本文考虑粘结层厚度对叠层压电悬臂梁结构的发电性能以及粘结层的抗剪性能进行分析，模型如图1 所示，其x、y 及z 轴的几何尺寸分别为L、w 及h（h=2hp+hm+2ht），hp 为压电层的厚度，hm 为基底层的厚度，ht 为粘结剂的厚度。应用中为了获取较大的电压，压电陶瓷采用串联方式，极化方向相反且沿着z 轴方向，电极面为垂直于z 轴的上下两面。当悬臂梁压电结构在自由端受到外荷载F（或竖向位移）作用时，压电结构产生弯曲变形，假设压电陶瓷与金属基底之间的力与位移是连续的。根据弯曲变形的特点，上、下层压电陶瓷表现为一层伸长另一层缩短。此时，压电陶瓷内将产生垂直于极化方向的线应变，通过压电材料的本构方程[10]可知，由于正压电效应的存在，压电陶瓷上下表面就形成了一定的束缚电荷，从而形成电势差。

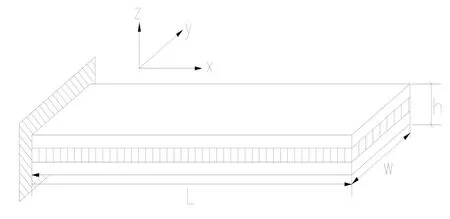
图1 悬臂压电梁几何示意图 Fig.1 Schematic diagram of the piezoelectric cantilever beam geometry

研究表明[11-12]，悬臂梁结构的压电振子可产生最大的挠曲变形，同时具有较低的谐振频率，对于悬臂梁矩形压电振子，当不考虑粘结剂影响时，其输出电压U 与自由端施加外荷载的关系为：

输出电压与端部挠度的关系为：

可见，在一定外力作用下，随着梁的弯曲变形就可以产生一定的电压，而对于叠层压电振子而言，若粘结剂的抗剪强度不足时，压电振子的基底层、压电层还会出现分离，这将大大降低压电振子的抗弯刚度，从而导致结构抗弯强度不足的破坏；但若粘结层过厚时，将增大压电振子的刚度，从而提高了压电振子的振动频率，这对利用环境振动能进行发电的压电振子而言将是非常不利的，因此，本文对叠层压电阵子结构进行仿真分析、参数优化，分析粘结层对压电振子发电性能及抗剪性能的影响。

2 叠层压电振子有限元建模

本文应用ANSYS 软件对图1 所示考虑粘结层厚度的悬臂梁叠层压电振子进行仿真分析，其中压电陶瓷采用Solid5 单元进行模拟，金属基底采用Solid45 单元，粘结剂采用Solid45 单元进行模拟。通过几何模型的建立、参数及单元类型设置后采用映射的方式进行网格划分，并对压电陶瓷片进行电压耦合，使压电陶瓷表面形成等势面，最后通过施加悬臂梁边界约束条件和电压边界条件，得到悬臂梁压电振子的有限元分析模型，该模型的材料参数及模型尺寸由表1 列出。

表1 复合结构中初始尺寸及材料性能参数表 Table 1 Initial geometric and material parameters used in the composite structure

（续表）

3 粘结层厚度对压电振子电压、基频的影响分析

压电振子基频与产生电压的研究是压电振子结构优化设计的理论基础，由于环境中的振动频率较低，设计压电振子时，在条件相同情况下，使基振频率低，同时能产生相对较大的电压，成为最终确定压电振子设计尺寸的依据。本文研究了改变悬臂梁叠层压电阵子粘结层厚度对压电阵子的开路电压及一阶固有频率的影响关系，在自由端施加1 N 的集中外荷载，仿真分析得到悬臂梁叠层压电振子输出电压与粘结层厚度的响应关系以及一阶固有频率与粘结层厚度的响应关系，如图2 和图3 所示。

图2 粘结层厚度与电压的关系 Fig.2 The relationship between the thickness of the adhesive layer and the voltage

由图2、图3 可见，随着压电振子粘结层厚度逐渐地增加(由0.01 mm 增大到0.08 mm)，叠层压电振子的一阶频率基本成线性增加，而开路电压却有不同程度的减小，当粘结层厚度为0.08 mm 时，压电振子开路电压约为不考虑粘结层厚度时的73%，但频率却增加不到15%，可见，考虑粘结层后，对压电振子的基频的增幅并不是很大；为可获得较大电压、谐振频率较低的压电振子，起到高效采集环境中低频振动能量的目的，本文进一步研究了粘结层厚度不同时，压电振子产生的电压与频率的比值之间的关系，图4 给出粘结层厚度不同时压电振子产生的电压与频率之间的比值关系。

图3 粘结层厚度与一阶频率的关系 Fig.3 The relationship between the thickness of the adhesive layer and the first order frequency

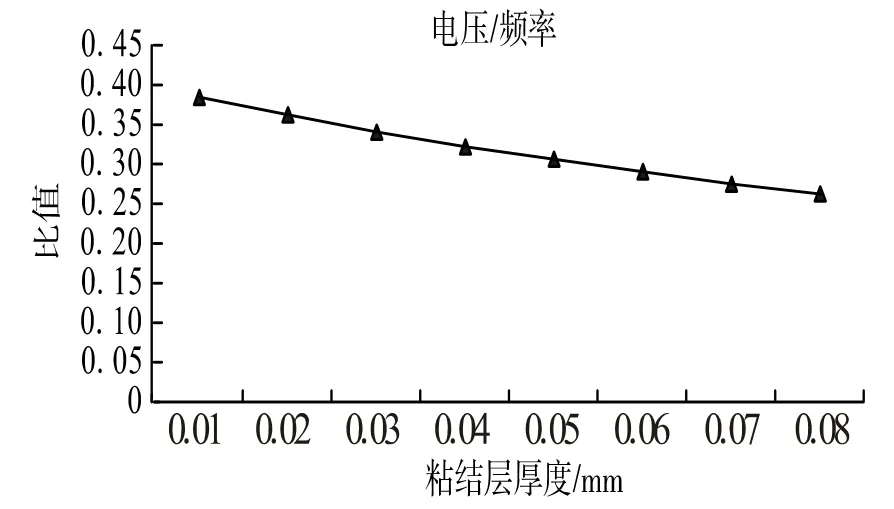
图4 电压与频率的比值随粘结层厚度的关系 Fig.4 The ratio of the voltage and frequency of the relationship with the thickness of the adhesive layer

由图4 可以看出，当粘结层厚度为0.01mm 时，电压与频率的比值最大，即该尺寸叠层压电振子对低频振动的环境能量转换的效率最高，因此，在保证叠层压电振子抗剪强度的前提下，叠层压电振子中的粘结层厚度不应过厚。

4 静力作用下压电振子粘结层切应力随粘结层厚度的关系

当悬臂梁叠层压电阵子发生振动时，压电振子发生弯曲变形，此时，压电振子结合面上将产生一定的切应力，当粘结剂抗剪强度不足时，叠层压电振子将会在结合面上发生剪切破坏，由受弯构件切应力分析知，切应力越靠近截面中心轴越大，对于双晶压电梁，结合面处将产生较大的切应力，因此，图5 给出悬臂梁叠层压电振子自由端截面上粘结层与基底结合面上的切应力随粘结层厚度时的变化关系。

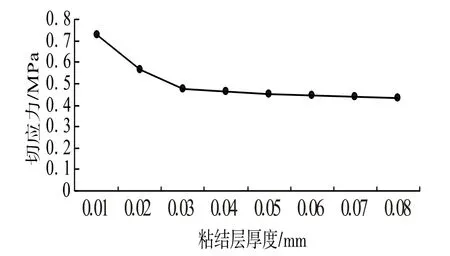
图5 粘结层厚度与切应力的关系 Fig.5 The relationship between the thickness of the adhesive layer and the shear stress

由图5 可以看出，在相同条件下，当粘结层厚度增加时，自由端粘结层所在结合面上的切应力有一定程度的减小，但是当粘结层厚度大于0.04mm时，其对粘结层抗剪性能的提升作用已不再显著；此外，当粘结层厚度为0.08 mm 时，产生的切应力约为粘结层厚度为0.01mm 的0.6 倍，由此可见，在相同外力作用下，增加粘结层厚度可有效减小叠层压电振子结合面处的切应力。因此，在制作矩形悬臂梁叠层压电振子时，为防止叠层结构在结合面上发生剪切破坏，可以考虑粘结层厚度对压电振子的抗剪强度的影响。

5 结语

文中利用ansys 软件，对不同厚度粘结层悬臂梁叠层压电振子进行有限元仿真分析，结果表明，在相同外力作用下，随着叠层压电振子粘结层厚度的增加，虽然压电振子的开路电压有所减小、结构的基频线性增加，但是随着粘结层厚度的增加，会使压电振子自由端结合面上切应力有较大程度的减小，这对制作矩形悬臂梁叠层压电振子时，为防止叠层结构在结合面上发生剪切破坏具有重要指导意义。

[1]LEFEUVRE E, BADEL A, RICHARD C, et a1. A comparison between several vibration-powered piezoelectric generators for standalone systems[J]. Sensors and Actuators A, 2006, 126: 405-416.

[2]龚立娇. 收集弯曲振动能量的压电式发电机： 中国，CN101262189[P], 2008-09-10.

[3]Gong L, Shen X, Li J. Experimental investigation of energy harvesting from triple-layer piezoelectric bender[C]//Applications of Ferroelectrics, 2009. ISAF 2009. 18th IEEE International Symposium on the IEEE, 2009: 1-6.

[4]ROUNDY S, WRIGHT P K. A piezoelectric vibration based generator for wireless electronics [J]. Smart Mater Struct, 2004, 13: 1131-1142.

[5]邓冠前，陈仲生，陶利民，等. 基于压电振子的振动能量捕获行为研究[J].压电与声光，2009,31(6):938-942.

[6]霍晓青. 悬臂型压电能量采集器固有频率和能量输出特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[7]王玉山，龚立娇，王锐. 铜-压电陶瓷复合型不同形状悬臂压电振子发电性能分析[J]. 压电与声光，2013,35(3): 395-397.

[8]石斌，胡敏强，朱壮瑞.粘结层对超声马达定子振动特性的影响[J].中国电机工程学报,2001，21(7):72-77.

[9]王玉山, 龚立娇, 王锐. 粘结层对不同形状叠层压电振子发电性能的影响[J]. 压电与声光，2014,36(2): 234-236.

[10]张福学. 现代压电学[M]. 北京: 科学出版社，2001.

[11]Kim S, Thomas J. Johnson. Harvesting energy from a cantilever piezoelectric beam[C]// Bellingham:Proceedings of SPIE–The International Society for Optical Engineering，2004, 5386: 259-268.

[12]WANG Qingming, CROSS L E. Theoretical analysis of the sensor effect of cantilever piezoelectric benders [J]. J Applied Physics, 1999, 85(3):1702-1712.