动力总成悬置支架多目标拓扑优化和强度分析

全伟，孙涛，林全斌，上官文斌

（1.华南理工大学机械与汽车工程学院，广东广州510640；2.宁波拓普集团股份有限公司，浙江宁波315800）

汽车悬置支架是汽车动力系统的重要组成部件，起着支撑发动机，阻隔发动机向车架传递振动的作用[1-2]。悬置支架强度不足，在部分工况下会造成悬置支架断裂，严重影响安全[2]。同时，在悬置系统中，悬置支架质量大，成本高。因此，对悬置支架进行设计时，既需要满足各种工况下的强度要求，又要做到节省材料，降低成本[3]。

本文中以汽车悬置支架静态多工况下的柔度和动态振动固有频率为目标函数，对汽车悬置支架进行多目标拓扑优化设计。基于变密度的拓扑优化方法[4-5]，采用多刚度和平均频率拓扑优化的目标函数，通过优化得到同时满足静态柔度最小和低阶频率最大要求的拓扑结构，避免了单目标拓扑优化无法获得全局最优解的缺点。

以某轿车的悬置支架为分析对象，利用Nastran软件计算得到悬置支架的应力大小、分布云图以及模态分布云图[4]，在此基础上对不满足强度要求的悬置支架采用密度法材料插值模型，进行拓扑优化，并根据优化结果设计出符合强度要求和减少材料的结构。

1 悬置支架强度分析

采用Hypermesh软件对整个悬置支架进行网格划分，网格类型为二阶四面体单元。悬置支架为铸铝件，材料为AlSi9Cu3；螺栓为铸铁件，材料为ZG340-640；两材料属性见表1。通过对悬置系统载荷工况的分析[6]，得出悬置支架强度的载荷工况（表2）。在悬置支架上施加集中载荷，对螺栓连接处进行全约束，施加的载荷和约束见图1。

表1 支架材料参数

计算过程中，为提高计算精度，将实体单元和蒙皮单元转为二阶，计算得到悬置支架强度。悬置支架在工况1 下的最大应力为180 MPa，超出了材料的屈服强度160 MP，会发生断裂现象，需对支架进行改进。支架在不同工况下的强度，悬置支架的应力分布云图见图2。

表2 悬置支架强度的载荷工况

图1 支架有限元约束

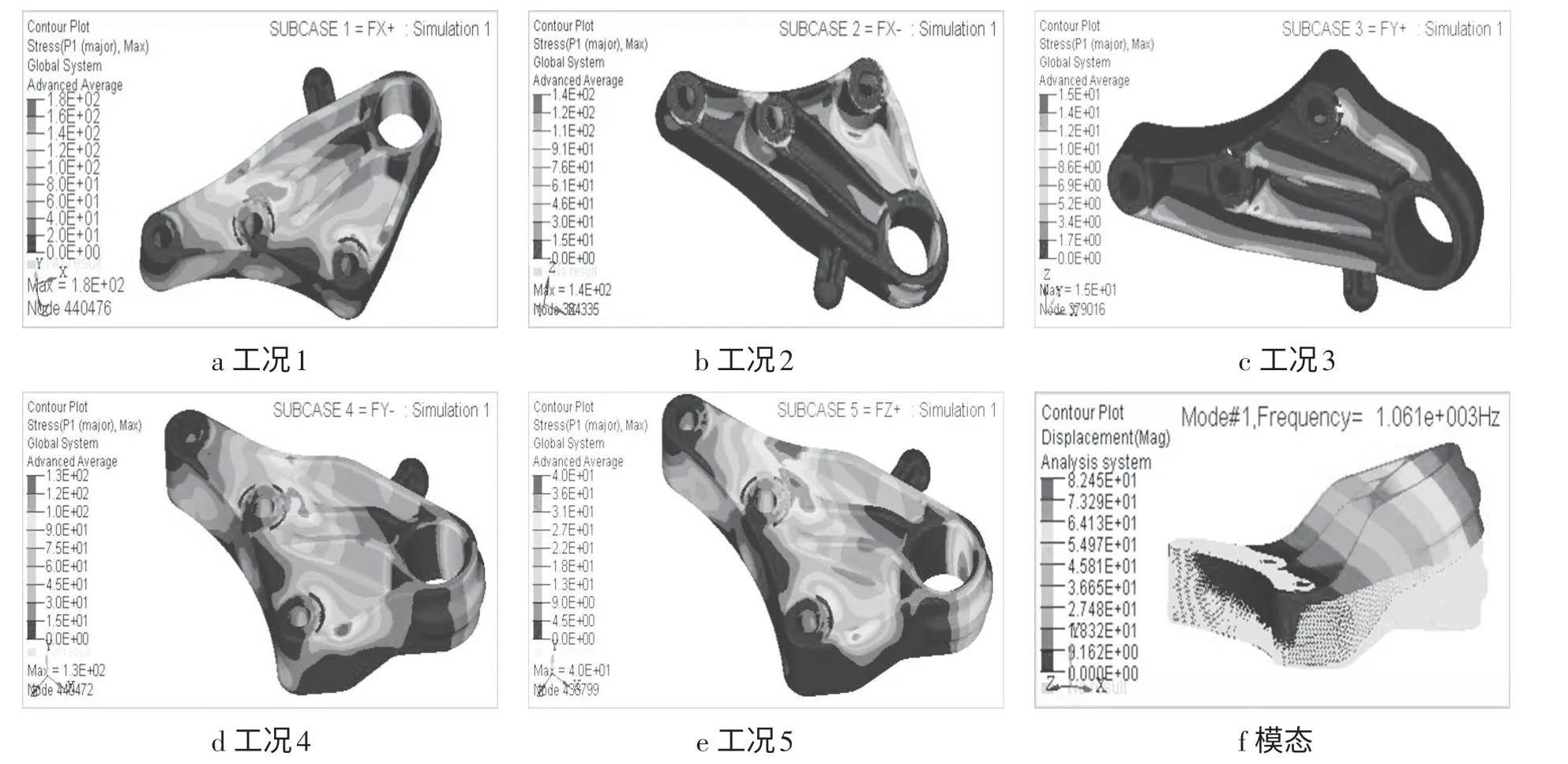
图2 悬置支架的应力分布云图

2 悬置支架拓扑优化

进行支架分析所用的前处理器软件为Hypermesh，Optistruct和Nastran作为求解器，利用Hyperview 进行后处理。首先对不满足强度要求的悬置支架进行改进，满足强度和模态要求，在此基础上合理优化结构，使支架应力分布更加均匀，降低支架的最大应力，达到减少材料的目标。

2.1 拓扑优化区域

拓扑优化时，先确定支架的优化区域和非优化区域。优化区域作为拓扑优化的基础，要考虑零件的安装边界。由于该支架通过3个螺栓固定在变速箱上，所以螺栓连接处为非优化区域，其余部分为优化区域，如图3所示。

图3 优化区域示意图

2.2 目标函数和约束条件

多工况下的刚度拓扑优化问题通常称作为多刚度拓扑优化问题。每一个工况对应一个刚度的最优结构拓扑，一般来说，不同的载荷工况将得到不同的结构拓扑。采用折衷规划法研究多工况拓扑优化问题。通常把刚度最大问题等效为柔度最小问题来研究，柔度则用应变能来定义。由折衷规划法结合功效函数法可得到多刚度拓扑优化的目标函数：

式中：m为载荷工况数；n为单元总数；wk为第k个工况的权值；q为惩罚因子，q≥2；Ck(ρ)为第k个工况的柔度目标函数和分别为第k个工况柔度目标函数的最大值和最小值。

动态固有频率拓扑优化将低阶的几阶重要频率的最大化作为目标函数，并将结构体积作为约束函数。采用平均频率公式来定义固有频率拓扑优化的目标函数：

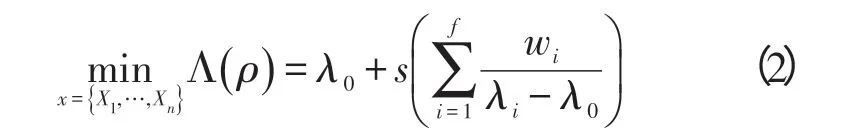
式中：Λ(ρ)为平均频率；λi为第i阶特征频率；λ0和s为给定的参数，用来调整目标函数；wi为第i阶频率的权重系数；f为需优化的低阶频率阶次。

结构多目标拓扑优化是以体积作为约束，同时考虑静态多刚度目标和动态振动频率目标的拓扑优化。由折衷规划法结合平均频率法可得到多目标拓扑优化的综合目标函数：

式中：F(ρ)为综合目标函数；w为柔度目标函数的权重；Λmin和Λmax分别为频率函数的最小值和最大值，用来消除量刚。

本文中的拓扑优化方法采用的是变密度法，优化区域确定后，需确定目标函数和约束函数，即响应函数。本次优化中，需要考虑质量、柔度和应力等响应。加权柔度中，选择用来优化的载荷步；体积分数设定的对象为设计空间集合，所以本次优化的函数如下：

优化目标：加权柔度最小，频率≥600Hz

优化约束：优化区域的体积分数＜45%

最大应力＜160MPa

2.3 优化结果

优化过程中，由于原模型部分强度超过材料的屈服强度，强度不满足要求。针对初步处理的模型，进行材料填充，重新建模。

进行拓扑优化时，设定设计变量、优化响应和优化目标等参数后，通过迭代计算，可得到拓扑优化结果。经过27步迭代后，得到模型，见图4。

根据优化结果，对悬置支架模型进行细化设计，对重新设计的悬置支架方案进行网格划分，得到优化后模型，见图5。

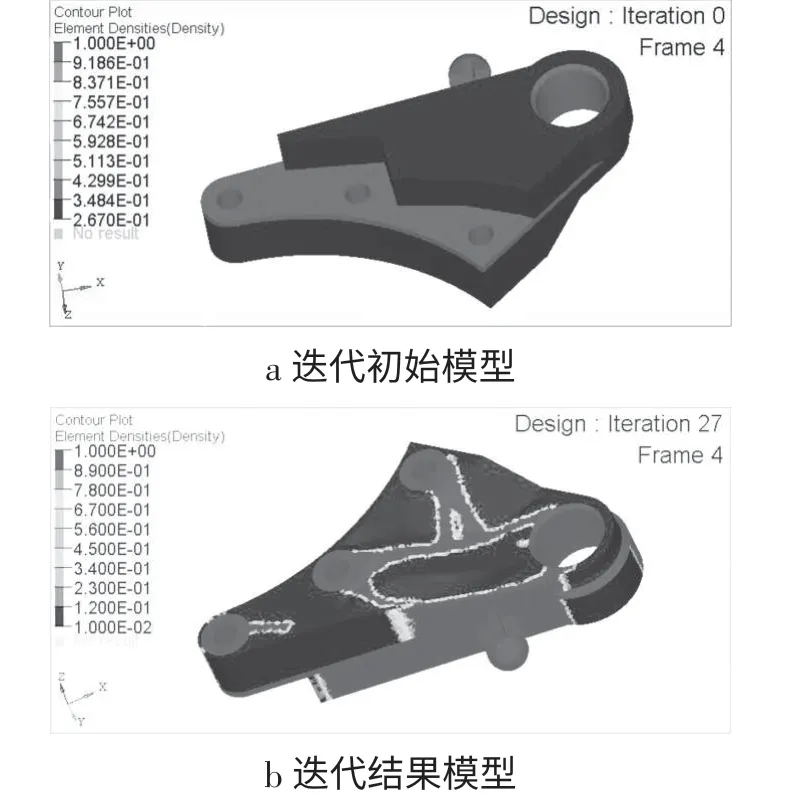
图4 拓扑优化结果

图5 优化后支架设计方案

3 优化前后支架强度和质量对比

为了对优化设计方案与原方案进行全面比较，对优化后的支架进行同工况的强度分析，应力模态云图见图6。优化前后支架分析结果见表3。由表3可知，各工况下，优化后的支架能满足强度和模态频率（不小于600Hz）要求，同时优化后材料比原材料减少12%，可见拓扑优化设计对结构性能改进效果比较明显。

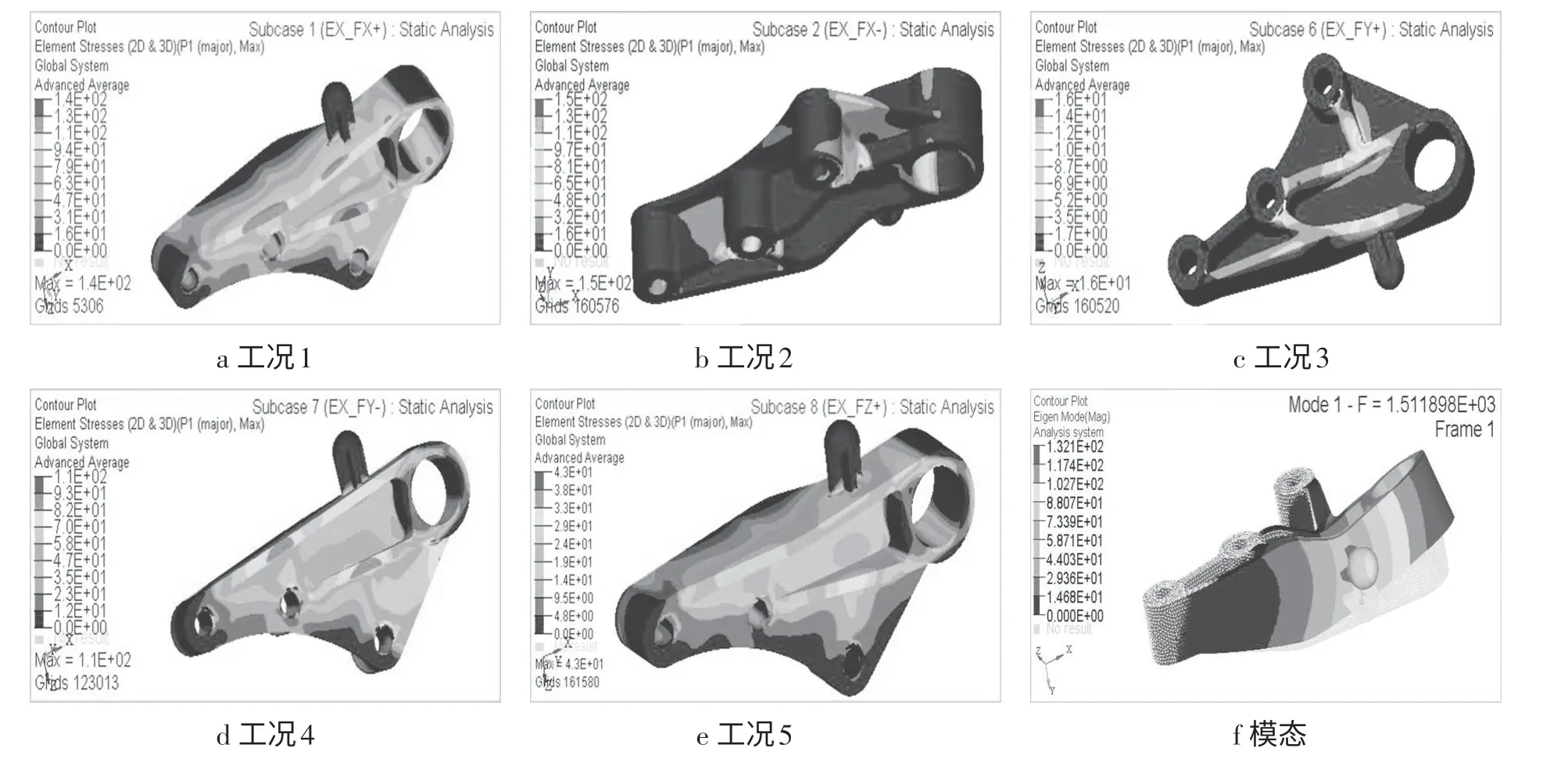
图6 拓扑优化结果

表3 优化前后分析结果比较

4 小结

基于变密度的拓扑优化方法，采用多刚度和平均频率拓扑优化的目标函数，通过对悬置支架进行优化设计，经过计算和实验验证，可在允许的设计空间里合理布置材料，以最少材料获得较优结构强度、刚度和稳定性。本文中支架的优化方法和支架强度的分析方法对动力总成悬置支架设计提供了前期的计算分析，减少了悬置支架的开发周期。

[1]赵艳青，刘本元，上官文斌.汽车动力总成悬置支架的优化设计[J].汽车科技，2007（3）：53-55.

[2]潘孝勇，柴国钟，刘飞，徐驰.悬置支架的优化设计与疲劳寿命分析[J].汽车工程，2007，29（4）：341-345.

[3]戴永谦.应力和位移约束下连续体结构拓扑优化设计及其在汽车设计中的应用[D].淄博：山东理工大学，2002.

[4]隋允康，杜家政，彭细荣.MSC.Nastran有限元动力分析与优化设计实用教程[M].北京：科学出版社，2004.

[5]SIGMUND O.A 99 Line Topology Optimization Code Written in Matlab[J].Structural and Multidiscipline Optimization，2001（21）：120-127.

[6]上官文斌，徐弛，黄振磊，李歧，李涛.汽车动力总成悬置系统位移控制设计计算方法[J].汽车工程，2006，28（8）：738-742.

[7]李楚琳，徐伟伟.动力总成悬置系统的优化设计[J].湖北汽车工业学院学报，2009（1）：1-3+14.