基于虚拟样机技术的三轴车辆模型验证研究

石坤，刘西侠，袁磊

（装甲兵工程学院机械工程系，北京100072）

多轴车辆与一般的两轴车辆相比，存在单轴载荷较重、轴距较短和重心偏高等特点。国内某型前两轴转向的三轴车辆（6×6）簧载质量为15.8 t，最大行驶速度88 km·h-1，最小转弯半径约9.02 m。该车前、中桥采用机械拉杆式转向机构，这种转向机构在一定程度上减少了轮胎磨损，但也导致了其低速行驶时转向半径相对偏大，高速时车辆的操纵稳定性欠佳，限制了该车转向性能的有效发挥。因此，对该车转向性能进行深入分析，具有重要意义。

全轮转向技术能够在低速时减小车辆转向半径、高速时改善车辆的操纵稳定性，并在国外已经应用于实车。日本丰田的“悍马”Mega Cruiser 军用越野车辆，采用一套全轮转向系统，能够让车体长5.09 m的巨大车身拥有5.6 m的最小转向半径，而同级别采用前轮转向车辆的转向半径则是9 m；可见，全轮转向技术能有效改善车辆的转向性能。国内在这方面的研究逐渐深入，思路基本上是一致的，都是通过建立相关的数学模型，按照一定的控制策略，实现车辆的全轮转向，然后通过相关动力学软件建立模型并仿真分析车辆的响应，最终在车上实现全轮转向技术[1]。

为设计三轴车辆的全轮转向系统，本文中建立了车辆的二自由度数学模型以及虚拟样机模型。通过实车转向性能试验来验证所建立模型的正确性，并对虚拟样机模型进行修正，使之能够很好地模拟实车转向行驶性能，为全轮转向系统设计提供理论和试验依据。

1 三轴车辆数学模型建立

1.1 车辆运动坐标系

车辆的运动是借助固结在车辆上的车辆坐标系（动坐标系）来描述的，如图1所示，固结在车辆上的oxyz 直角坐标系为车辆坐标系[2]。oxy平面为车辆的左右对称平面，当车辆在水平路面静止时，坐标系的x轴平行于路面并指向前方，y轴平行于路面指向驾驶员左侧，z轴垂直于路面并指向上方，坐标系的原点o 常与车辆质心重合。坐标系中分别定义了车辆的3个平动和3个转动自由度，其中和车辆操纵稳定性的主要参量为：y轴方向的侧向加速度v、侧向加速度ay和z轴上的横摆角速度ωr。

图1 车辆坐标系

1.2 轮胎模型

图2为车轮俯视图。图2a表示车轮在自身的旋转平面内运动；图2b表示车轮运动方向偏离其自身的旋转平面，也就是车轮有侧向滑动。车轮中心平面与其行驶方向的夹角为侧偏角当车轮发生侧滑时，将产生一个抵抗侧滑的反作用力——侧偏力[3]，其垂直于车轮旋转平面。

车辆转向时，其轮胎受力[4-5]如图3所示。图中Fx为地面切向反作用力；Fy为轮胎侧偏力；δ为车轮转角；o点为车辆质心；a，b和c分别为前桥、中桥和后桥到质心的距离；B为轮距。

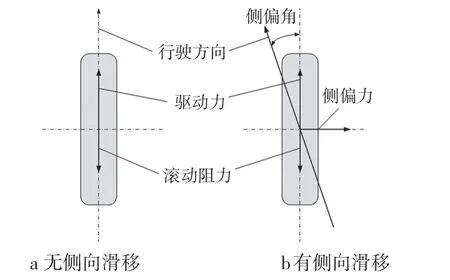
图2 车轮侧偏力

图3 车辆转向行驶时的受力

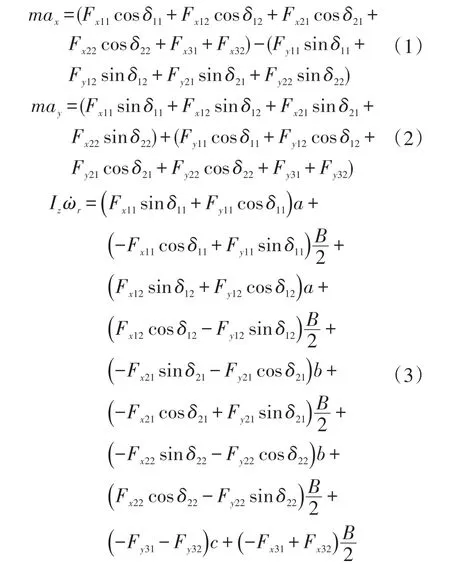
式中：m为整车质量；ax为车辆的纵向加速度，Iz为车辆绕z轴转动惯量；r为横摆角加速度。

1.3 线性二自由度单轨模型建立

描述车辆运动的线性二自由度模型[6-7]基于以下假设：1）忽略转向系统，将转向轮转角作为输入；2）不考虑车辆绕x轴的侧倾角、绕y轴的俯仰角和沿z轴的位移；3）规定车辆沿x轴的速度u 不变，因此车辆只有2个自由度；4）车辆的侧向加速度在0.4 g以下；5）忽略地面切向力对轮胎侧偏特性的影响及轮胎回正力矩的作用；6）忽略空气动力的作用；7）不考虑左右轮胎载荷变化对其特性的影响。

建立的线性二自由度车辆模型只有沿y轴的侧向运动和绕z轴的横摆运动2个自由度，令车辆的质心与车辆坐标系的原点重合，可得到如图4所示的车辆二自由度单轨模型。

根据二自由度模型所受到的外力、外力矩与车辆运动参数之间的关系，可得到二自由度车辆的运动微分方程[8-9]：

图4 三轴车辆线性二自由度单轨模型

式中：u，v分别为车辆质心在x轴和y轴的速度；δ1，δ2分别为前、中桥车轮转向角；Cα1，Cα2，Cα3分别为前、中、后桥轮胎侧偏刚度；β为车辆质心侧偏角；ωr为车辆横摆角速度；m为车辆质量；Iz为车辆绕z轴的转动惯量；a，b，c分别为前桥、中桥、后桥到车辆质心的距离。

由δ1和δ2近似线性关系[10]，令δ2=k′δ1，所以式（4）又可以写为

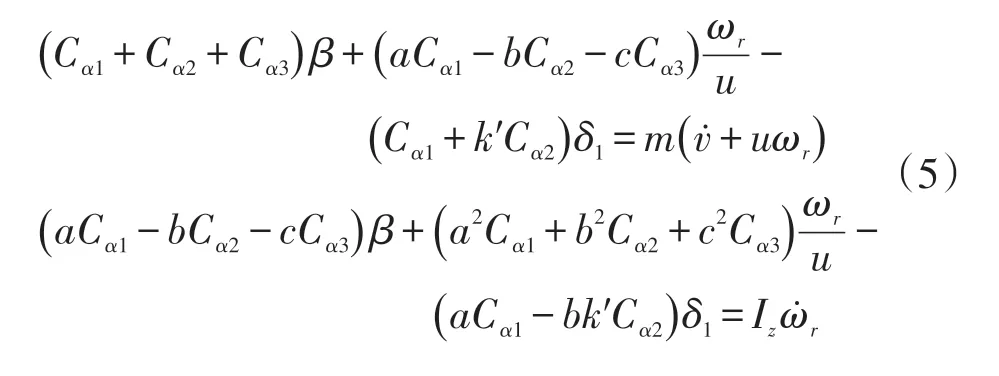
1.4 车辆稳态响应分析

车辆稳态响应分为不足转向、中性转向和过多转向，车辆应具有适度的不足转向特性[11]。通常用稳态的横摆角速度和前轮转角之比来评价稳态响应，这个比值叫稳态横摆角速度增益[12]。

稳态响应时，车辆的横摆角速度ωr为定值，此时r=0=0，代入式（5）得：

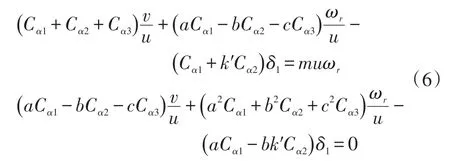
将式（6）消去v，得到稳态横摆角速度增益为

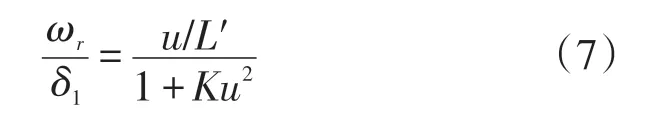
式中：

此时可将三轴车辆等效为两轴车辆，L′为等效后的两轴车辆轴距，K为等效后的车辆稳定性因数。通过分析等效后的两轴车辆稳态横摆角速度增益，得出三轴车辆的稳态响应特性。

已知三轴车的基本参数如表1所示。

表1 该三轴车辆结构参数

将表1数据代入式（9）可得K=0.0003，L′=2.65，则

因为K大于0，所以该车具有不足转向特性[13]。其特征车速为

当u为209 km·h-1时，车辆的稳态横摆角速度增益值取得极大值。由于该车的最大速度为88 km·h-1，即24.4 m·s-1，所以最大稳态横摆角速度增益为

1.5 车辆转向半径理论计算

线性二自由度单轨模型车轮转角为车辆左右车轮转角之和的平均值，例如：当车辆方向盘转动981°时，车辆左前轮的转角为31°，右前轮的转角为24°，则单轨模型车辆前轮转角为27.5°。同理，当车辆方向盘转动720°时，单轨模型前轮转角为20.2°；当车辆方向盘转动360°，单轨模型前轮转角为10.1°。

不考虑轮胎侧偏角对车辆转向半径的影响时，单轨模型后轮的转向半径R1为

且

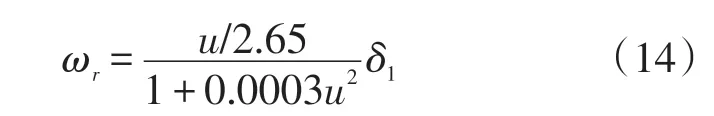
则车辆的转向半径R为

当单轨模型前轮转角 δ1分别取10.1°，20.2°和27.5°，车辆速度u分别为6.9 km·h-1，11 km·h-1和15.4 km·h-1时，可算得车辆的转向半径（表2）。

表2 单轨模型车辆转向半径mm

2 虚拟样机模型转向性能分析

2.1 虚拟样机模型建立

将三维软件SolidWorks中建立的车辆底盘模型导入动力学软件ADAMS/View中，构建该车的虚拟样机模型。对该车模型的所有构件添加质量、按实车约束情况在ADAMS中添加约束、添加路面、对分动器的输入齿轮添加驱动。为了能够实现仿真，需要建立轮胎模型、路面模型、悬架模型以及转向机构球铰接模型等，进而完善该虚拟样机模型。以轮胎模型及球铰接模型为例进行说明。

ADAMS软件提供了5种轮胎模型[14]，在此根据实际选择UA轮胎模型。UA轮胎和其他轮胎一样，也采用原地位于轮胎接地中心的TYDEX-W坐标系，如图5所示[15]。

图5 轮胎运动坐标系

UA轮胎模型中，轮胎垂直力为

滚动阻力矩为

式中：CZ为轮胎的径向刚度；δ为轮胎的径向变形；f为滚动阻力系数；γ为车轮的外倾角。

轮胎受到的纵向力FX、侧向力FY及回正力矩MZ，可分别根据轮胎的侧偏角、外倾角和轮胎所处状态来计算。

采用14.00R20型子午线无内胎轮胎，根据表3所示的轮胎特性参数定义轮胎特性文件。

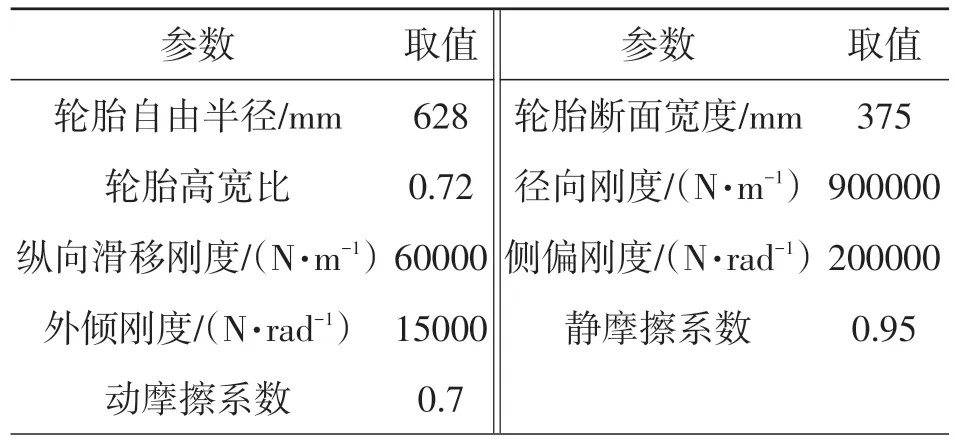
表3 14.00R20轮胎特性参数表

在双前桥转向系统中，转向拉杆之间、拉杆与转向节臂之间、悬架上下摆臂与转向节之间都采用球铰连接。行驶中的车辆能够抵抗外界微小干扰，保持行驶稳定性的关键原因就在于转向系统中的球铰存在摩擦。因此在添加转向系统球铰约束时，要添加适当的摩擦系数。设置转向系统中球铰副的静摩擦系数为0.5，动摩擦系数为0.3，摩擦力矩为0.5 N·m[16]，得到三轴车辆的虚拟样机模型。

2.2 模型转向性能分析

虚拟样机模型转向系统的输入为转向垂臂，方向盘转动360°相当转向垂臂转动16.53°；方向盘转动720°相当转向垂臂转动33.06°；方向盘转动981°（方向盘打到底），相当转向垂臂转动45°。图6为车辆速度为6.9 km·h-1，转向垂臂分别转动45°、33.06°、16.53°时车辆质心的运动轨迹图。

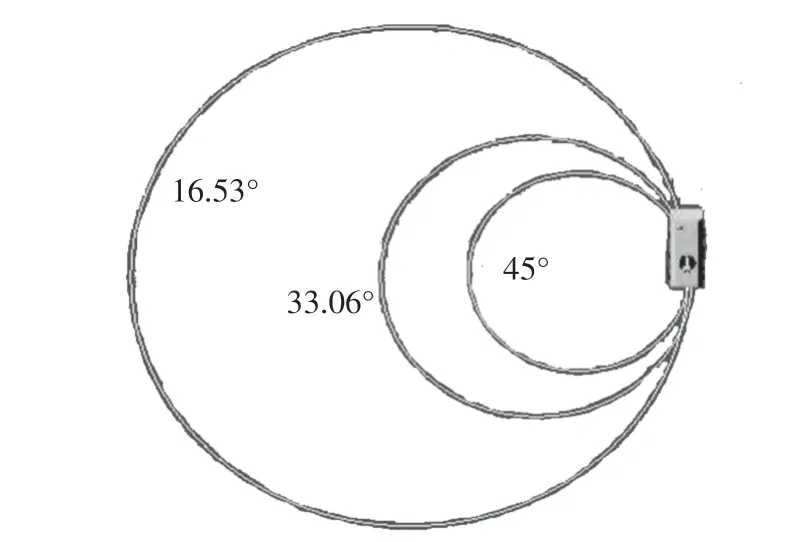
图6 稳态转向行驶车辆质心轨迹

根据车辆的运动轨迹图，可得各种工况下虚拟样机模型稳态转向时的转向半径，如表4所示。

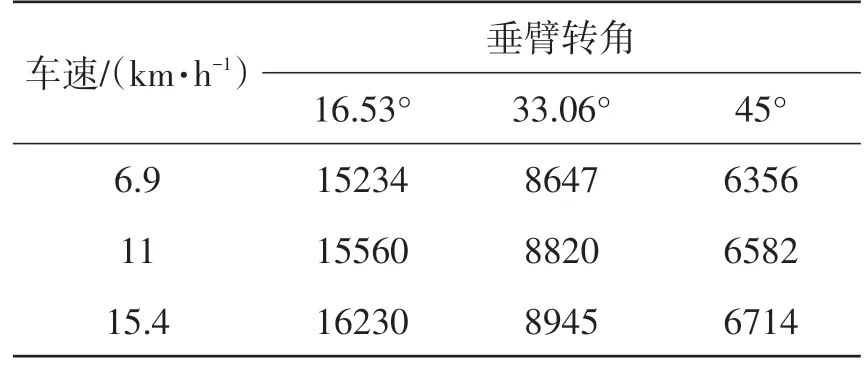
表4 虚拟样机模型车辆转向半径mm

由表2跟表4对比得知，由二自由度模型计算得到的转向半径与虚拟样机模型仿真所得转向半径差异较大，例如在6.9 km·h-1、前轮转角为10.1°（垂臂转角为16.53°）时，两者相差367 mm。另外，2次计算所得结果均不能反映车辆真实情况，因此需要通过实车试验所得数据来验证模型的正确性。

3 模型试验验证

实车试验目的是验证所建车辆虚拟样机模型的准确性，为虚拟样机模型的修正提供系列参数。

3.1 实验方案设计

车辆静止时，驾驶员启动发动机并将方向盘从平衡位置打到另外一个位置，然后固定方向盘，使车辆转向轮的转角保持不变。接着驾驶员挂挡并将油门踩到底，使轮式装甲车辆匀速行驶一周。在车辆转弯行驶的同时，车上的实验操纵人员打开安装在车体上水箱的开关，使管子漏水，进而在地面上得到车体前后4个点的运动轨迹。测量地面上的4个水迹圆的直径，即装甲车体上4个位置的转向直径，然后通过几何计算，得到车辆的转向半径。

3.2 实验内容

驾驶员在车辆静止时，分别转动方向盘360°、720°和981°，挡位分别挂爬行挡、1挡和2挡，将油门踩到底（控制车速与模型仿真车速相同），使车辆逆时针等速圆周行驶一圈，分别测量地面上4个水迹圆的直径，即可得到点A～D的转向直径，进而可以利用几何关系算出车辆的转向半径，如图7所示，图中标出了车体相关位置的尺寸，单位为mm。

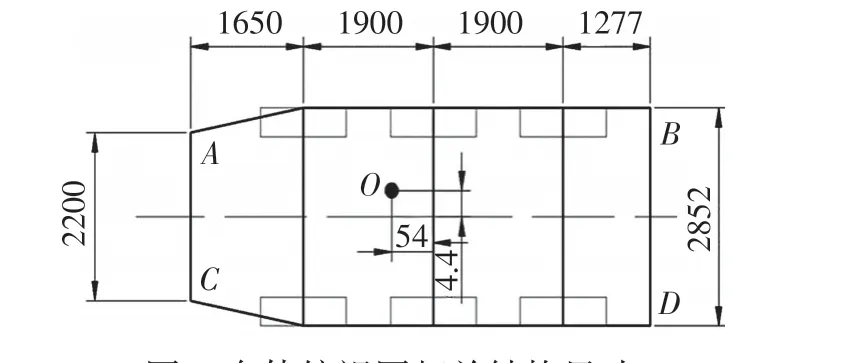
图7 车体俯视图相关结构尺寸

3.3 试验数据处理

通过测量地面上水迹圆的直径就可以得到相应车体上各点的转向直径，分别在3个不同的位置测得3 组直径值，然后取平均值。由所测得的车辆在3种工况下车体上4个点的转向直径值，根据几何作图法，便得到车辆行驶的转向半径。首先以车体上的点A～D为圆心，以这4个点各自的转向半径值做圆，如图8a所示，图中为方向盘逆时针转动720°，车辆挡位挂爬行挡，油门踩到底时的数值，图中单位为mm。

车辆做逆时针等速圆周行驶，车辆的转向瞬心肯定在图上点K附近。图8b为图8a在点K附近的局部放大图，车辆在此工况的瞬时转向中心O′肯定在点1～4所围成的封闭区域内。分别量得点1～4到质心点O的距离，然后求平均值，可近似得到车辆的转向半径。

图8 作图法求车辆转向半径示意图

根据上述车辆转向半径的求法，分别求得各工况车辆的转向半径，如表5所示。

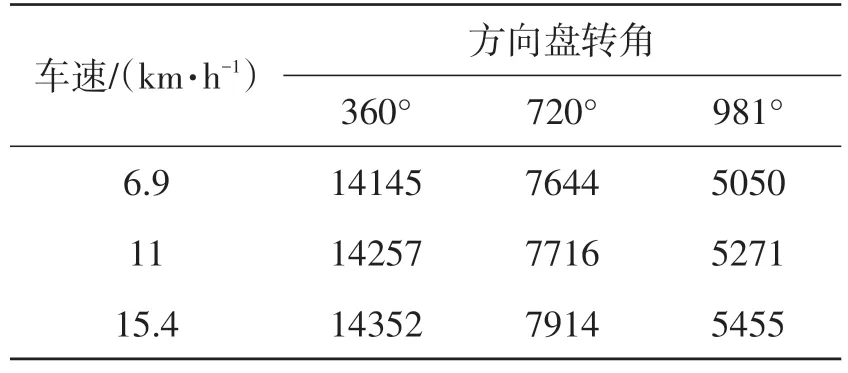
表5 各工况下车辆转向半径mm

表5与表2和表4对比可知，车辆在同一行驶工况下，利用二自由度模型计算所得的车辆转向半径较之虚拟样机模型仿真所得结果更加接近实车试验结果，这说明所建立的虚拟样机模型精确度不高，还需要进行修正。

4 虚拟样机模型修正

将轮胎的侧偏刚度调整为210000 N·rad-1、轮胎与路面的动摩擦系数调整为0.75、转向系统球铰接的摩擦力矩调整为2 N·m。虚拟样机模型在同样的工况下进行稳态转向仿真，得到车辆的转向半径，如表6所示。

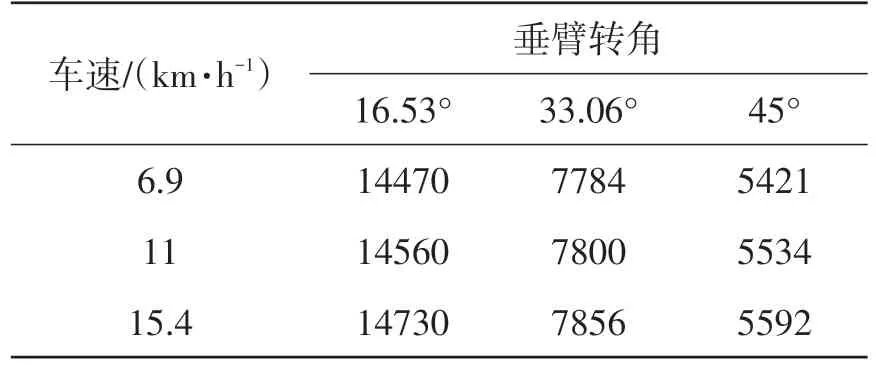
表6 虚拟样机模型车辆转向半径mm

对比表6和表5可知，在同一工况下，虚拟样机模型仿真分析结果与实车实验结果非常接近，这说明了经过修正的虚拟样机模型可靠性很高，能够很好地代表实车转向性能。

5 结论

建立了三轴车辆二自由度数学模型，并进行了车辆转向性能计算；搭建了该车虚拟样机模型，并进行了初步仿真分析。通过实车试验对模型进行验证与修正，结果表明：1）所建立的二自由度数学模型与实车试验所得结果较为吻合，证明了该数学模型的正确性；2）初步搭建的虚拟样机模型与实车行驶情况有较大偏差，可通过实车试验手段对模型进行修正；3）修正后的虚拟样机模型仿真结果能与实车试验数据较好吻合，说明修正后的模型具有较高可靠性，能很好地模拟实车转向行驶性能。

[1]洪升耀，徐国英，刘西侠，陈靖然.三轴车辆全轮转向系统设计及转向性能分析[J].机械研究与应用，2013，26（3）：20-22.

[2]余志生.汽车理论[M].北京：机械工业出版社，2012.

[3]D.Li,X.Shen,F.Yu.Integrated Vehicle Chassis Control with a Main/Servo-Loop Structure[J].International Journal of Automotive Technology,2006,7（7）∶803-812.

[4]S.Caglar Baslamisli,I.Emre Kose,G.Anlas.Gain Scheduled Integrated Active Steering and Differential Control for Vehicle Handling Improvement[J].Vehicle System Dynamics,2008∶1-20.

[5]J.Y.Zhang,J.W.Kim,K.B.Lee,et al.Development of an Active Front Steering（AFS）System with QFT Control[J].International Journal of Automotive Technology.2008,9（6）∶695-702.

[6]巩建坡，王树凤，贺翠华.极低车速下三轴转向车辆机动性的分析与验证[J].山东理工大学学报：自然科学版,2012，26（2）：1-5.

[7]郭孔辉.汽车操纵动力学原理[M].南京：江苏科学技术出版社，2011.

[8]H.Nozaki.Driver Steering Model and Improvement Technique of Vehicle Movement Performance During Drift Running[J].International Journal of Automotive Technology,2006,7（4）∶449-457.

[9]陈永生.轿车稳定性控制系统的状态参数估算及控制算法研究[D].长春：吉林大学，2010.

[10]宋海军，张继平，刘西侠，等.三轴车辆全轮转向控制系统研究[J].车辆与动力技术，2011（1）：1-5.

[11]Gerardo Gomez,John M.Starkey.Indirect Measurement of Tire Slip and Understeer/Oversteer[C].Motorsports Engineering Conference and Exhibition,2006∶1844-1852.

[12]陈雯.四轮转向汽车的运动特性及操纵稳定性分析[J].山东交通科技，2005（3）：87-89.

[13]喻凡，林逸.汽车系统动力学[M].北京：机械工业出版社，2008.

[14]吕佳.基于虚拟仿真的高速公路车—路条件下动态限速值研究[D].重庆：重庆交通大学，2009.

[15]王东杰.半挂汽车列车弯道行驶横向稳定性分析[D].山东：青岛理工大学，2008.

[16]姬鹏.面向主观评价的汽车转向系统建模与仿真研究[D].长春：吉林大学，2010.