概率型Cauchy-Schwarz不等式的一个推广

雷国梁，岳田

（湖北汽车工业学院理学院，湖北十堰442002）

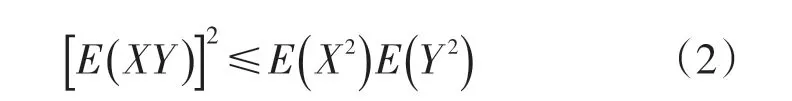
上述不等式在近现代数学的各个分支中都扮演着重要的角色，比如Hilbert 空间理论、古典实分析、复分析、数值分析、概率统计、微分方程定性理论中都有其广泛的应用。近年来，对于离散型Cauchy-Schwarz不等式的推广与改进相关方面的研究成为一个热点问题，并取得了丰富的成果[2-5]。本文中给出不等式（2）的一个概率型推广，并对其一种特殊情形进行研究，这样将一些离散型Cauchy-Schwarz不等式的经典结论推广到了概率空间。

1 Cauchy-Schwarz不等式(2)基于4个自由参数的推广

定理1对于2个随机变量X、Y，若存在，且有4个参数p,q,r,s ∈R，则有以下不等式成立：

其中系数由矩阵方程给出：

不等式（3）等价于

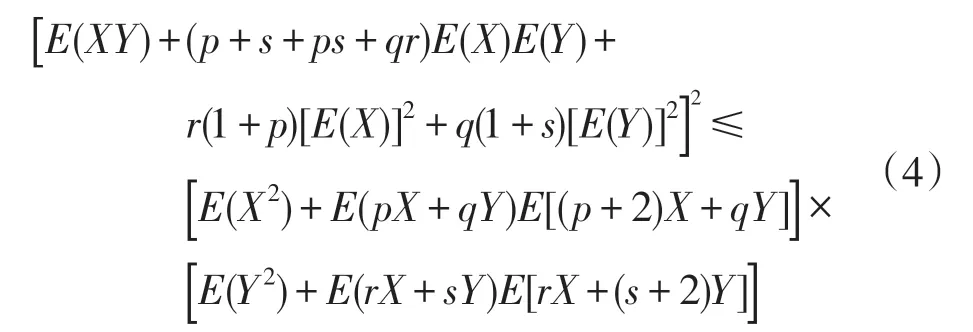
由此可见，当不等式（3）在Aj=Bj=Cj=0的特殊情况下，则Cauchy不等式（2）即为不等式（3）的一个推论。在式（3）中等号成立条件为

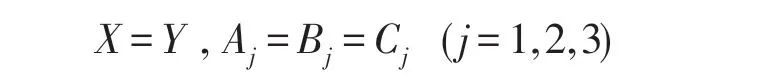
证明设非负二次多项式Q(x;p,q,r,s)（满足映射Q∶R→R）如下：

其中p,q,r,s ∈R。由此经过计算得出

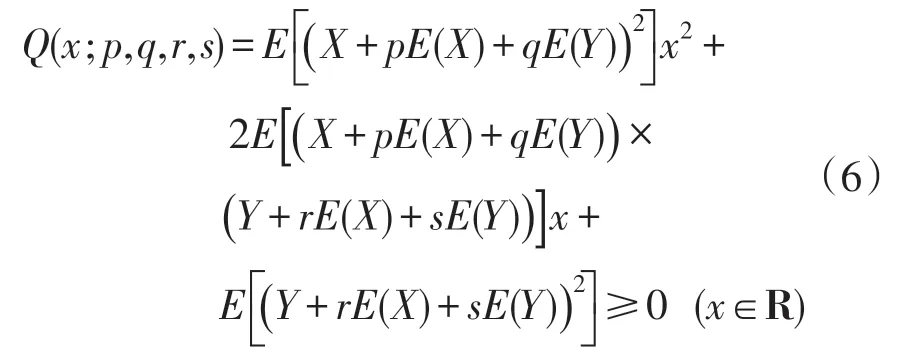
则多项式Q的判别式Δ 一定非正，即

所以用式（8）～（10）中各式对式（7）进行替换，则定理1的第1部分结论成立。

下面证明第2 部分（换言之，等号成立条件），假定Y=νX，且将其在式（3）中进行替换，则得到：

经过一些计算，以上等式导出下面的非线性系统：

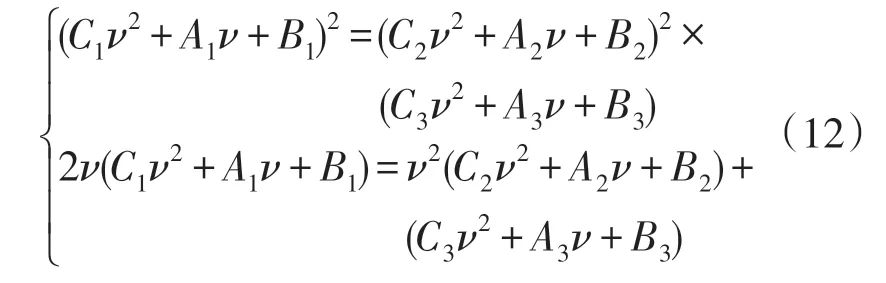
显然Aj=Bj=Cj(j=1,2,3)和ν=1为方程组（12）的一组解。

注定理1存在各种不同的子情形。然而，由于页面的局限性，这里只考虑不等式（3）的一种特殊情形并探究其子情形。自然地对于其他特殊情形可以类似进行研究。

2 当B1=C1=0时的特殊情形

对于不等式(3)当B1=C1=0时，一共有4种情形发生：1）

2.1 在式(3)中当q=r=0,且p,s ∈R的情形

在这种情况下，有B1=C1=A2=C2=A3=B3=0且不等式（3）被简化成如下形式：

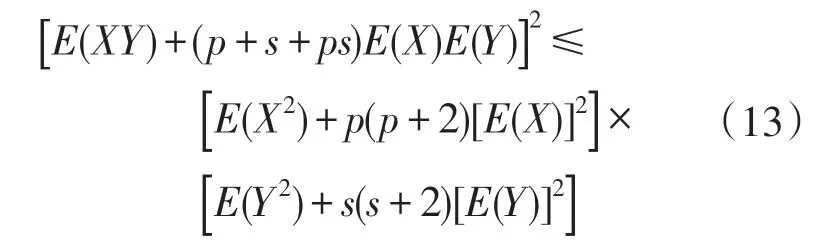
不等式（13）的一些较有意义的子情形如下所述。

2.1.1 情形1∶p=s ∈R(-2,0)（Wagner不等式的推广）

下面的不等式即著名的Wagner不等式的概率形式：设随机变量X和Y，若E(X2)和E(Y2)存在，且w≥0，则有

由结论推出式（14），足以假定在式（13）中有

对p=s ∈R(-2,0) 而言这显然成立，且当w=p×(p+2)≥0时，很容易得出Wagner不等式(14)。

若在式(13)中设p(p+2)≤0 且s(s+2)≤0，则有

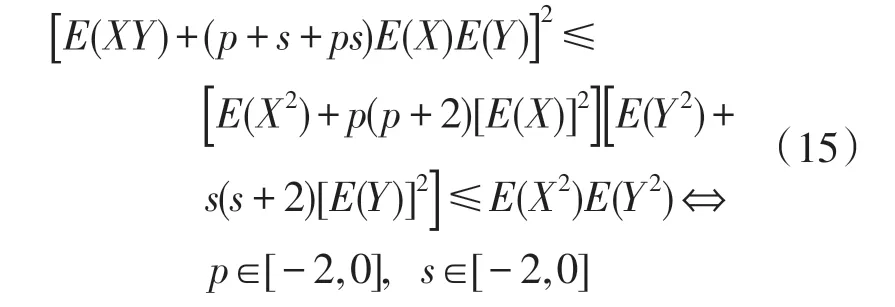
2.1.2 情形2∶p=s ∈[-2,0]（Cauchy不等式的改进）

假设在不等式(13)中p=s ∈[-2,0]且 令p(p+2)=u，因此u ∈[-1,0]。由此假设可得Cauchy不等式的一个改进。首先考虑下面的不等式，它可直接通过代数计算来进行证明：

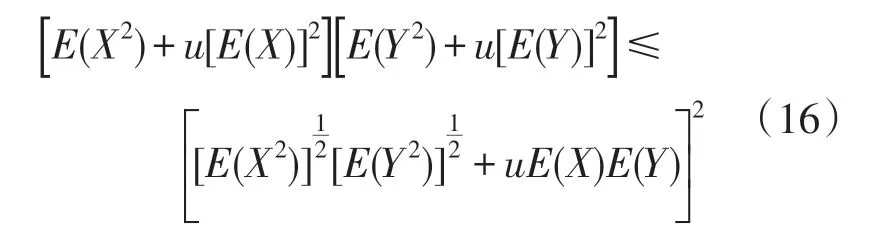
而且有

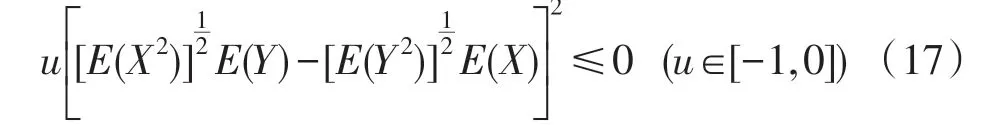
因此，参照不等式（13）和式（16），可得推论1。

推论1对于2个随机变量X和Y，若E(X2)和E(Y2)存在，且有α ∈[0,1]，则有

此不等式等价于：

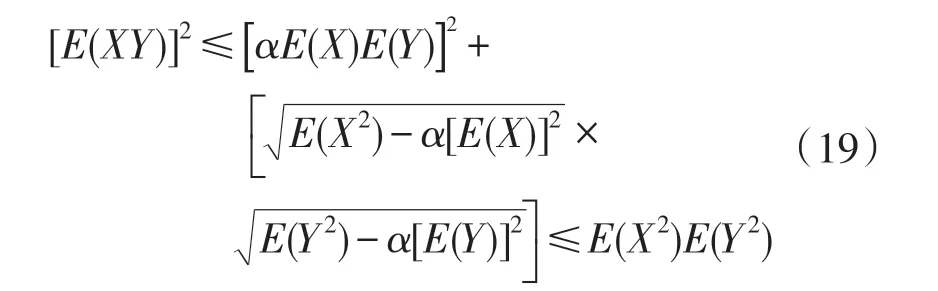
2.1.3 情形3

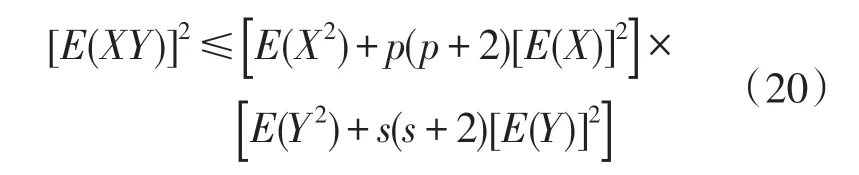
式中令p=s=-2，即为Cauchy不等式（2）。

2.2 在式(3)中当r=0,s=-1且p,q ∈R的情形

在这种情况下，有B1=C1=A3=B3=0，则不等式（3）可简化为如下形式：

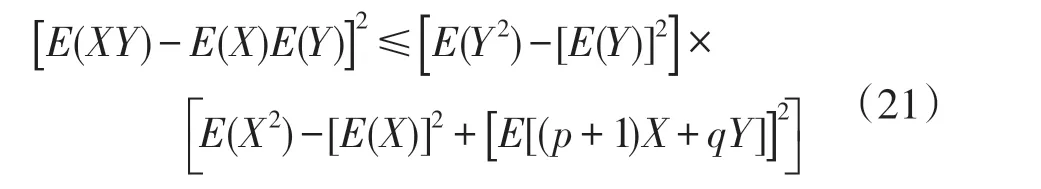
然而，由于

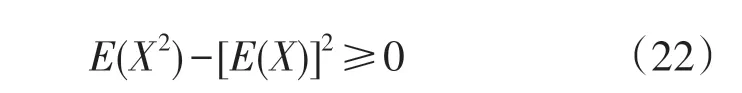
故在式（21）中当p=-1，q=0时即为最佳选择。此外注意到第3）种情况即p=-1，q=0 且r,s ∈R，将给出与式（21）同样的结果。

2.3 在式（3）中当p=s=-1且r,q ∈R的情形

这种情况下，则有B1=C1=A2=A3=0，且不等式（3）可简化为如下形式：

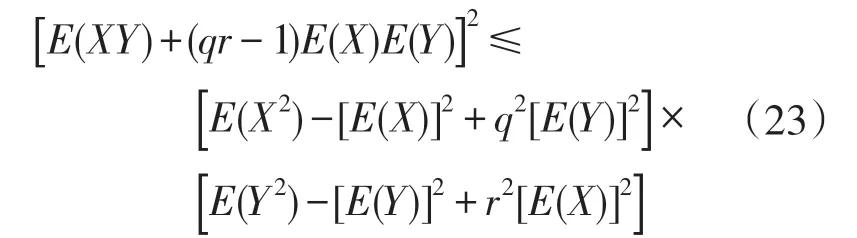
在式（23）中当q=r=1时，将出现一个有意义的情形。即导出如下不等式：

[1]Cauchy A L.Cours D′analyse de L′ Ecole Royale Polytechnique Part1∶Analyse Algbrique[M].Paris：Guthier-Villars,1821.

[2]Masjed-Jamei M.A Functional Generalization of the Cauchy-Schwarz Inequality and Some Subclasses[J].Appl.Math.Lett.,2009,22∶1335-1339.

[3]Masjed-Jamei M,Dragomir S S,Srivastava H M.Some Generalizations of the Cauchy- Schwarz and the Cauchy-Bunyakovsky Inequalities Involving Four Free Parameters and Their Applications[J].Math.Comput.Model.,2009,49∶1960-1968.

[4]Masjed- Jamei M.A Generalization of the Cauchy-Schwarz Inequality with Eight Free Parameters[J].J.Inequal.Appl.,2010∶Article 705168.

[5]Masjed-Jamei M,Hussain N.More results on a functional generalization of the Cauchy-Schwarz inequality[J].J.Inequal.Appl.,2012∶Article 239.