非线性压电振动能量采集器的振动特性与实验研究*

王光庆，张 伟，刘 创，杨斌强，廖维新

（1.浙江工商大学信息与电子工程学院，杭州310018；2.香港中文大学机械与自动化工程学系，香港999077）

非线性压电振动能量采集器的振动特性与实验研究*

王光庆1*，张 伟1，刘 创1，杨斌强1，廖维新2

（1.浙江工商大学信息与电子工程学院，杭州310018；2.香港中文大学机械与自动化工程学系，香港999077）

为了提高线性压电振动能量采集器的输出特性，在线性压电振动能量采集器悬臂梁末端引入Duffing非线性磁力，构造了一种双稳态非线性压电振动能量采集器；综合考虑能量采集器的动态振型与轴向应变分布情况，建立了系统非线性机电耦合集总参数运动控制模型，并利用4阶、5阶Runge-Kutta算法对能量采集器的非线性振动特性进行了数值模拟；利用谐波平衡法计算获得了能量采集器的幅频响应方程，数值分析了激励频率、激励幅值以及磁铁间距等对系统非线性振动特性的影响，发现双稳态运动可以极大地提高能量采集器的频率响应范围和能量采集效率，并且能量采集器在低频、低幅值激励情况下可以产生大幅值周期运动；最后，通过实验对数值计算结果进行了验证。

压电能量采集器；非线性振动特性；双稳态行为；Duffing非线性磁力

压电振动能量采集器是一种利用压电陶瓷的正压电效应将环境中的振动能量采集并转换成电能的微机电器件，在微电子设备和微功耗器件中具有广泛的应用前景［1］。典型压电振动能量采集器的结构是由压电陶瓷和金属弹性体粘结而成的悬臂梁结构，该结构简单、制造方便、与MEMS集成性好。但由于这种结构是一种线性系统，工作频带相对比较窄，难以与环境振动的宽频和随机特点相匹配；当压电能量采集器的谐振频率与环境振动源频率不一致时，能量采集器不能产生谐振，其能量采集和转换效率会大大降低［2］。最近研究表明，在线性压电振动能量器中引入非线性磁力，使之构成双稳态压电振动能量采集器，可以实现在微弱激励下的大幅值、宽频带的周期或非周期的高能轨道运动，从而实现能量采集器在非谐振状态下的结构大变形，提高能量采集和转换效率［2-3］。

Erturk［4］等将Duffing式双稳态模型用于压电振动能量采集器的分析与设计，通过理论与实验研究了双稳态压电悬臂梁的响应和输出性能，并提出了实现能量采集器作大幅值高能轨道振动的方法。Santon等［5］对双稳态压电悬臂梁进行了建模、数值计算和实验研究，得到了多吸引子共存、混沌和大幅周期运动等现象，并指出在磁场的作用下，压电能量采集器的振动势能函数是一个与振动幅值有关的多项式。Mann等［6］利用磁铁间的吸引力构造了一种非线性双稳态能量采集器，并建立了能量采集器的数学模型，理论计算与实验研究证明势能阱逃脱现象可以大大拓宽能量采集器的响应频带。Gammaitoni［7］等研究了双稳态非线性能量采集器的随机共振机理，并指出合理选择势能阱函数的参数，可以大大提高能量采集器在弱环境随机振动的能量采集与转换输出功率。Ferrari等［8］建立了双稳态压电悬臂梁的非线性方程，数值分析了悬臂梁在白噪声激励下的随机共振幅值响应。孙舒等［9］研究了双稳态压电悬臂梁发电系统的动力学模型，并计算分析系统的响应特性，发现双稳态运动可以提高系统的频率响应范围。崔岩等［10］建立了双稳态压电悬臂梁的数学模型，理论与实验研究证实了双稳态压电振子能够拓展能量采集器的谐振频率范围，并能提高能量采集器的低频振动能量采集效率，但对能量采集器系统的动力学行为未做深入研究。由于非线性压电振子的动力学行为比较复杂，且非线性模型的求解比较困难，如何从理论和实验角度深入揭示非线性特性对压电振动能量采集器性能的影响机理还缺乏统一的方法。此外，上述研究中未考虑能量采集器的动态振型和轴向应变分布对模型输出性能的影响。

本文引入Duffing非线性磁力模型，构造了一种双稳态非线性压电振动能量采集器；综合考虑能量采集器的动态振型与轴向应变分布情况，建立了系统非线性机电耦合集总参数运动控制模型，并利用4、5阶Runge-Kutta算法对模型非线性振动特性进行了数值模拟分析；利用谐波平衡法计算获得了能量采集器的幅频响应方程，数值分析了激励频率、激励幅值以及磁铁间距等对系统非线性振动特性的影响，最后，通过实验对数值计算结果进行了验证。

1 双稳态压电能量采集器模型

本文研究的双稳态压电振动能量采集器是在线性悬臂梁压电振动能量采集器的末端引入一对相互排斥的磁铁对，如图1（a）所示，永磁铁A固定在悬臂梁的末端，永磁铁B固定在距离悬臂梁自由端dr处，通过调节永磁铁A、B之间的间距dr可以改变磁铁排斥力FM的大小。当磁铁间距dr无穷远时，两磁铁之间的排斥力FM为零，压电振动能量采集器系统变成线性系统；当磁铁间距dr减小到某个值时，悬臂梁将出现三个静平衡点，其中包括两个稳定的静平衡点和一个不稳定的静平衡点，此时，系统表现出双稳态现象。

图1 双稳态压电能量采集器结构模型

图1 中FN和FR分别为磁铁排斥力FM在垂直和水平方向的分力。当在线性压电振动能量采集器中引入两永磁铁后，根据磁场力的计算方法，两磁铁在垂直方向上产生的排斥力FN与磁铁间距dr和悬臂梁末端振动位移x(t)有关，具体为［9］：

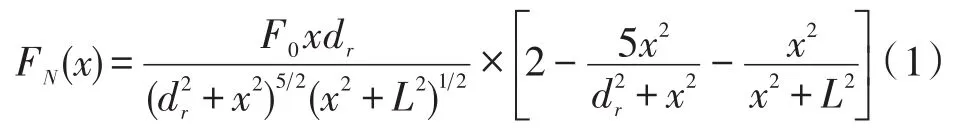
将式（2）所示的非线性磁力引入到图1（a）所示的结构模型中，得到系统的集总参数模型，如图1（b）所示。图中M、C和K分别表示线性悬臂梁压电振动能量采集器的集总等效质量、等效阻尼和等效刚度；α和Cp分别表示压电陶瓷的机电耦合系数和等效夹持电容，u（t）和y（t）分别表示基础和悬臂梁末端的振动位移，且x(t)=y(t)-u(t)，V（t）为负载电阻R两端的电压降。

图2中等效参数为［11-12］：

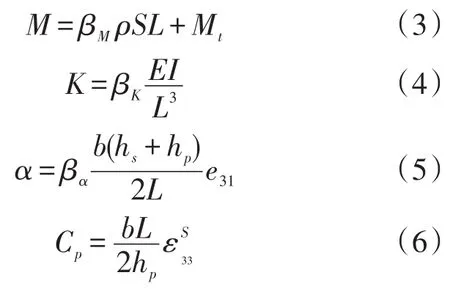
式中，ρ、S、I和E分别为线性悬臂梁压电振动能量采集器的平均密度、截面面积、截面惯性矩和平均弹性模量。e31和分别为压电陶瓷的压电常数和夹持介电常数，hs和hp分别为悬臂梁基板和压电陶瓷的厚度。 βM，βK和 βα为与悬臂梁振型信息ϕ(x)和轴向应变分布有关的待定系数，其中［11-12］：

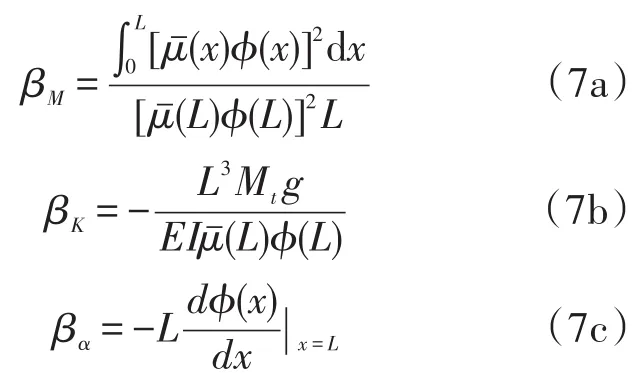
根据图1（b）所示的集总参数模型，建立系统的非线性运动控制方程，如下：

图2 系统非线性势能曲线

2 模型解分析

2.1 系统时域解分析

式（12）表示的非线性压电振动能量采集器机电耦合方程可以利用微分方程求解器得到其时域解，本文采用4-5阶龙格库塔算法（Ode45）在MATLAB仿真软件中求解获得。

2.2 系统频域解分析

采用谐波平衡方法对系统的频域解进行分析，由式（10）可得：

式（20）是一个关于振动幅值A的6阶非线性多项式表达式，该式存在1个或3个实数解。当存在3个实数解时，唯独最大和最小的两个实数解表示非线性系统是稳定可实现的，这意味着对于给定的外部激励频率和幅值，双稳态压电振动能量采集器具有两个稳态的谐波振动。

同理，将式（16）和式（17）代入式（11）可得双稳态压电振动能量采集器输出电压的幅值为：

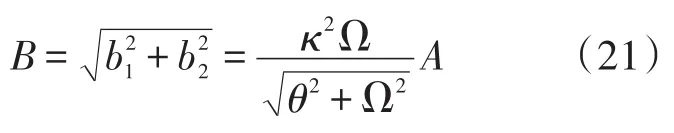
则双稳态压电振动能量采集器在一个振动周期内的平均输出功率为：

3 系统非线性特性仿真分析

本文仿真参数取：

①压电悬臂梁结构参数：平均密度ρ=7.844 1×103kg·m-3，截面面积 S=8.172×10-6m2，截面惯性矩 I=1.403 6×10-13m4，弹性模量E=7.001 8×1010Pa，α=7.143 7×10-4，Cp=70nF，悬臂梁长度L=60mm，

②磁铁参数：mA=mB=0.93×106A/m，VA= VB=0.6×10-6mm3。

将上述参数代入系统模型计算得到：μ=0.04，r=1.174，θ=1.030 1×10-5，κ2=0.058 9。

3.1 时域响应特性分析

图3是外部激励加速度的频率Ω=0.8，初始平衡位置X0=0.417 3时，非线性压电振动能量采集器的末端振动位移X、输出电压v以及相图等特性在负载电阻R开路条件下随外部激励加速度幅值（F=[0.02，0.08，0.20]）的变化情况。从图3可以看出，随着激励加速度幅值的增大，非线性压电悬臂梁能量采集器的末端振动位移、振动速度和输出电压都随之增大。当激励加速度幅值很小（F=0.02）时，由图3（a）可知，由于能量采集器输入的能量很小，不足以克服势能阱的阻碍作用，能量采集器被限制在初始平衡位置（X0=0.417 3）附近作小幅值的单稳态周期振动（或低能轨道振动），导致能量采集器的末端振动位移、振动速度、输出电压等较小。此时，相图是一个以圆心（0.417 3，0）的圆。当激励加速度逐渐增大，能量采集器开始由单稳态的周期振动变成为多周期振动，进而出现混沌-小幅值周期的拟周期振动；当激励加速度幅值增加到F= 0.08时，由图3（b）可知，能量采集器在两个势能阱之间作大幅混沌振动，并产生奇异吸引子；如果继续增大激励加速度幅值到F=0.2时，能量采集器则由大幅不规则的混沌振动变为在两个势能阱间作大幅周期振动（或高能轨道振动），如图3（c）所示。此时，能量采集器的末端位移、振动速度和输出电压等会大大提高，表现出大幅周期吸引子。

图4是外部激励加速度的幅值F=0.2，磁铁间距dr=12mm，初始平衡位置X0=0.417 3时，非线性压电振动能量采集器的末端振动位移、输出电压以及相图等特性负载电阻开路条件下随外部激励加速度频率（Ω=[0.4,0.8,1.6]）的变化情况。由图4可以看出，当激励频率很小时，由于激励远离系统非线性谐振频率，即使外部激励幅值很大，也很难激励能量采集器出现大幅值的振动，能量采集器只能在平衡位置附近作小幅值的周期振动。随着激励频率的增大，能量采集器逐渐进入混沌振动（图4（a））和大幅值周期振动（图4（b））；当激励频率增大远远超过其固有频率（Ω0=1.0）时，能量采集器又回到平衡点附近作小幅周期振动，如图4（c）所示。由此可见，要使能量采集器的输出特性增加，激励频率范围并非越大越好，而是低频范围下出现大幅振动。

图3 能量采集器末端振动位移X、输出电压V以及相图随激励加速度幅值F的变化

图4 能量采集器相图随激励加速度频率的变化

图5和图6是外部激励加速度的幅值F=0.2，激励频率Ω=0.8时，非线性压电振动能量采集器的相图在负载电阻开路条件下随磁铁间距dr的变化情况。由图5、图6可知，当磁铁间距dr在某个范围内，系统才会发生大幅值的高能轨道振动；当磁铁间距很小时，由磁力模型可知，系统中的非线性力很大，能量采集器很难有足够的能量越过势垒的阻碍作用作大幅振动，只能在平衡位置作小幅的周期振动，如图5所示。当磁铁间距趋于无穷远时，磁力作用变为0，此时，双稳态系统变为线性系统，能量采集器在中心平稳位置附近作小幅的周期振动，如图6所示。

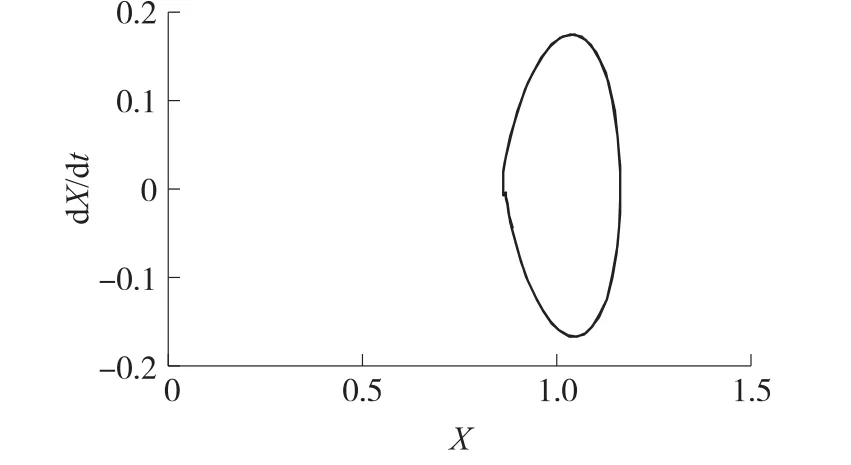
图5 dr=10.5 mm时系统相图

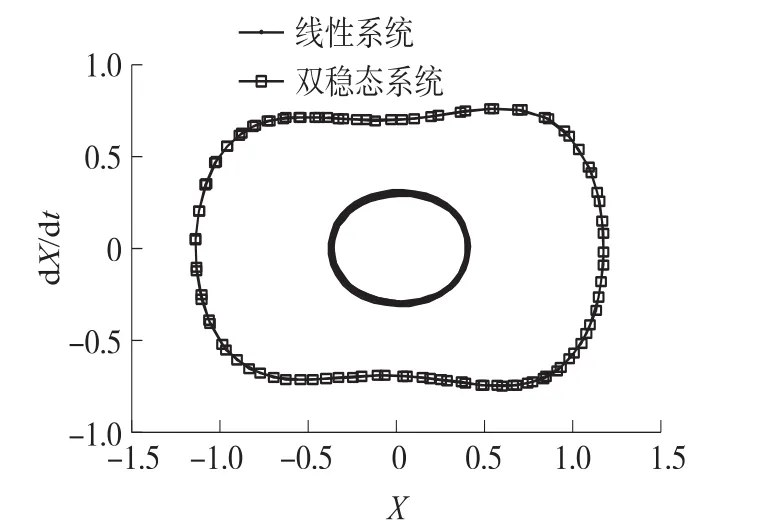
图6 双稳态系统与线性系统相图对比

3.2 磁铁间距的影响

图7是外部激励加速度的频率Ω=0.8，负载电阻R=136K时，非线性压电振动能量采集器的末端振动幅值在不同磁铁间距条件下随激励幅值的变化情况。

图7 不同磁铁间距下采集器末端位移幅值随激励加速度幅值的变化情况

由图7可知，系统末端位移幅值随着激励加速度的增加逐渐增加，但增加幅度逐渐减小。当磁铁间距dr=14mm时，系统在外部激励加速度幅值F=0.06发生跳变；当dr=12mm时，系统在F= 0.35发生跳变；当dr=11mm时，系统在F=0.66发生跳变。这是由于随着磁铁间距的增大，系统非线性磁力和势垒均减小，系统克服势垒的阻碍作用所需要的外部激励能量减小。反之，当磁铁间距减小时，由于系统需要克服较大的势垒才能跳跃到高能轨道振动，因此，需要较大的外部激励加速度；一旦系统跳跃进入高能轨道，则会产生较大的输出性能。

4 对比仿真分析

本文将非线性双稳态压电能量采集器的输出特性与线性压电能量采集器的输出特性进行对比分析。线性压电能量采集器的无量纲化运动控制微分方程如下［14］：

式中变量定义与式（12）是相同的。并可得到线性系统末端位移幅值表达式：

式中C=Ω3-(κ2+θμ)，D=-(μ+θ)Ω2+θ

非线性双稳态压电能量采集器末端振动相图与线性系统相图的对比结果如图6所示，可以看出，双稳态压电能量采集器较线性系统具有更高的位移、速度和电压输出特性。

5 实验与验证

非线性双稳态压电振动能量采集器实验系统如图8所示。双稳态压电振动能量采集器由线性双压电晶片能量采集器（尺寸：60×18×0.454mm，其中每片压电晶片厚度为0.127 mm，谐振频率为21.6 Hz）和一对永磁铁（磁铁体积600 mm3，磁矩0.93×106A/m）构成。双稳态压电能量采集器通过螺钉固定在激振器台面上，信号发生产生固定频率和幅值的正弦加速度信号，通过功率放大器后激励激振器作正弦运动，台面振动加速度通过加速度计进行监控，能量采集器的末端振动位移和速度则通过激光测振仪采集后，通过控制器送入计算机进行计算处理和分析；能量采集器的输出电压则通过示波器采集获取。实验过程中，磁铁间距可以通过螺旋测微机构进行调节，系统初始平稳位置为8 mm。

图8 双稳态压电振动能量采集器实验系统

实验中磁铁间距dr=14mm，此时双稳态能量采集器系统谐振频率为16.2 Hz，实验时选取激励频率 f=17Hz，逐渐增大激励幅值，测量双稳态压电振动能量采集器不同激励幅值下的影响特性。图9为激励幅值A=13m/s2时的实验现象，此时系统在初始平衡位置作小幅周期振动。当激励幅值增大到A=19m/s2时，系统发生幅值混沌运动，如图10所示；若继续增大激励幅值A=24.6 m/s2，则系统由混沌运动变为大幅值的周期运动，系统振动幅值达到15 mm，振动速度达到1 500 mm/s，如图11所示。此时，当若增大激励频率 f=23Hz时，由于激励频率远离系统谐振频率，系统恢复在初始平衡位置附近做小幅值的周期振动，如图12所示。图9～图12的实验结果与4.1节的理论仿真结果是一致的。

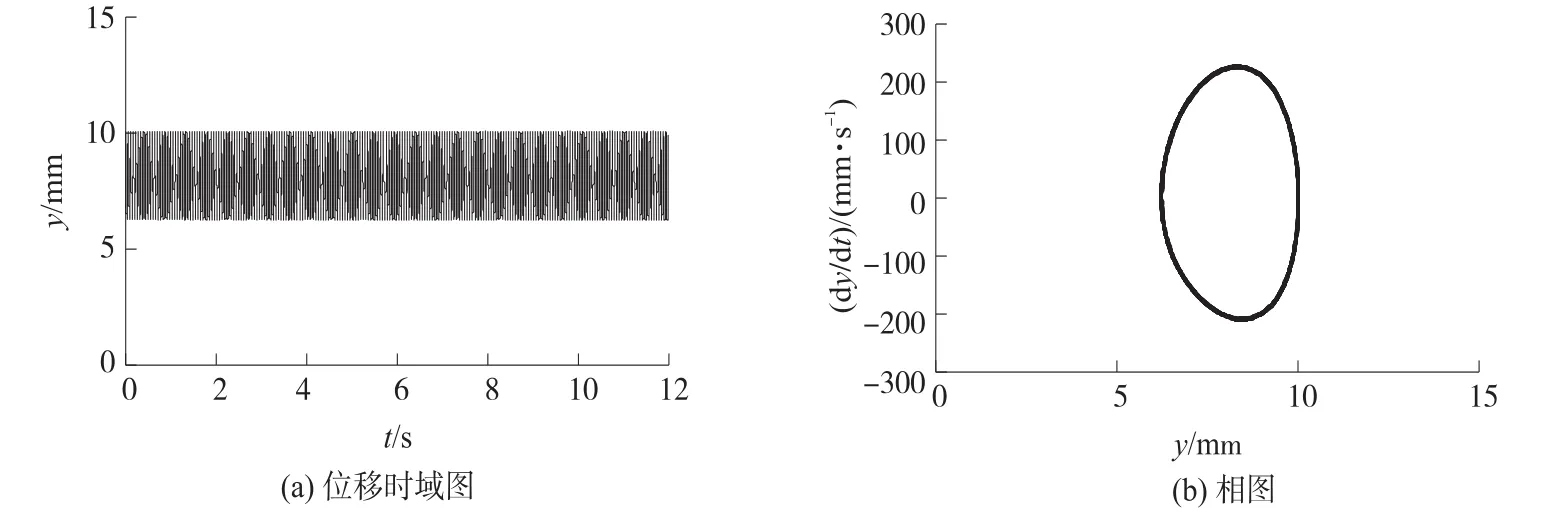
图9 末端位移时域图、相图实验结果（A=13m/s2，f=17 Hz，dr=14 mm）

图10 末端位移时域图、相图实验结果（A=19 m/s2，f=17 Hz，dr=14 mm）

图11 末端位移时域图、相图实验结果（A=24.6 m/s2，f=17 Hz，dr=14 mm）

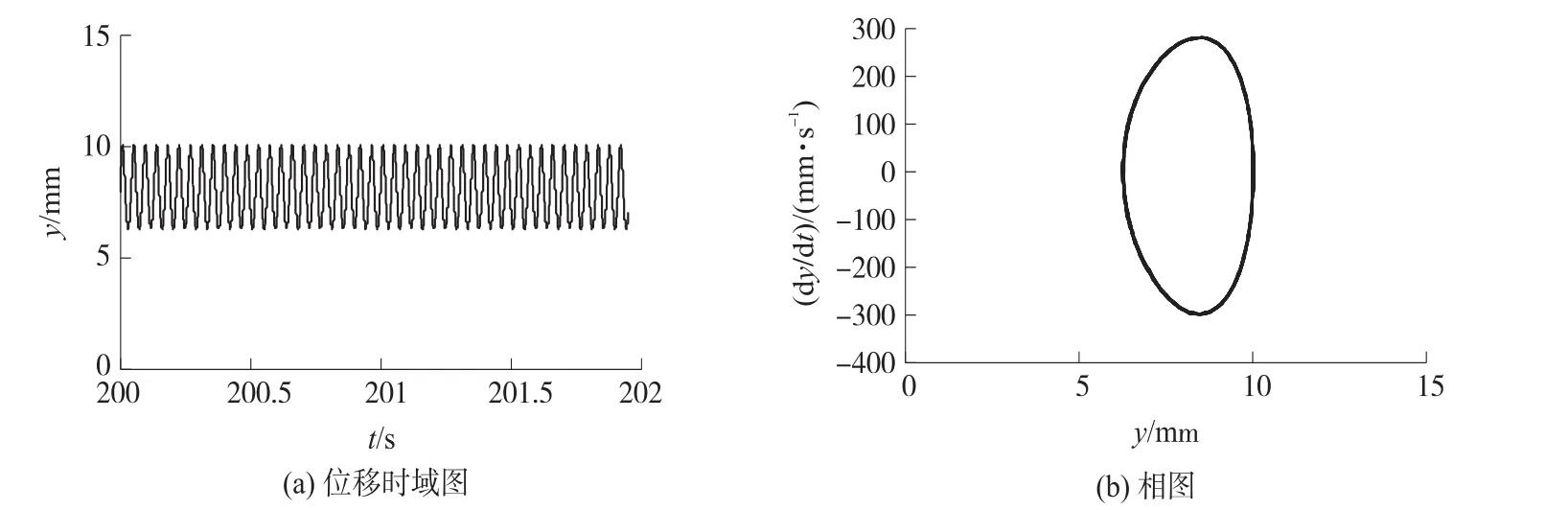
图12 末端位移时域图、相图（A=24.6 m/s2，f=23 Hz，dr=14 mm）

图13是激励频率 f=17Hz、激励幅值F=8m/s时磁铁间距dr对双稳态压电振动能量采集器输出性能的影响实验结果，从图中可以看出，当磁铁间距很小（dr＜11mm）时，由于此时磁铁之间的磁力很大，能量采集器没有足够的能量越过势垒做大幅振动，只能在一个平衡点附件做小幅周期振动，此时，系统末端输出位移幅值比较小；当且仅当磁铁间距在区间内dr∈[12,16]时，系统做大幅值的周期振动，并且表现为双稳态特征；随着磁铁间距dr的持续增大，磁铁间的磁力也持续减小直到为零，此时系统变为线性系统，其幅值输出将比双稳态周期振动时要小很多，这与4.1节的理论仿真分析是相符合的。

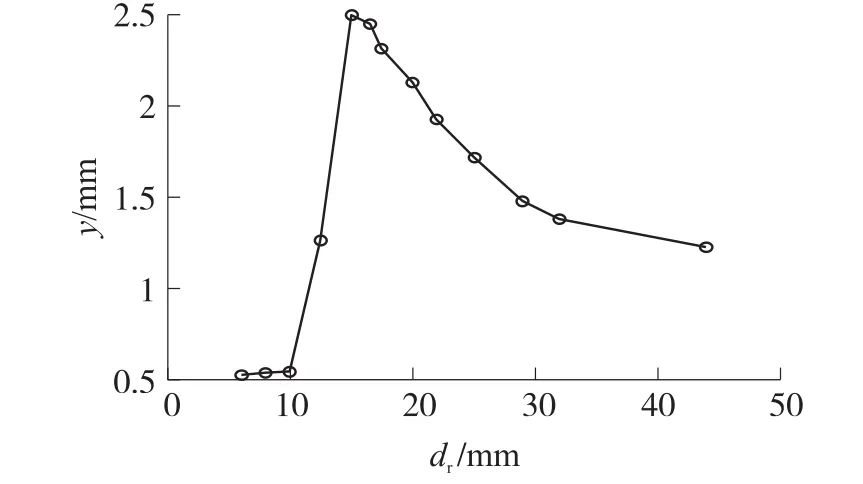
图13 磁铁间距对能量采集器末端位移的影响

图14是非线性双稳态压电振动能量采集器分别在无量纲激励幅值作用下的升频、降频响应实验结果。可以看出，随着激励幅值的增大，系统的频率响应幅值和作大幅值周期振动的频带宽均增大。由于非线性振动的影响，双稳态能量采集器的频率响应特性在升频激励过程中具有跳跃现象，这种现象容易使能量采集器由低能小幅值振动轨道瞬间进入高能大幅值振动轨道，从而极大地提高能量采集器的输出性能。此外，从图14中还可以看出，随着激励幅值的增加，不仅系统的振动幅值有所增大，而且系统出现跳跃现象的频率点逐渐提前，这有利于扩宽系统的频率响应带宽。在降频激励过程中，能量采集器的频率响应特性与升频过程中的频率响应特性存在滞后现象，这种现象主要是由于压电陶瓷材料的迟滞效应引起的。

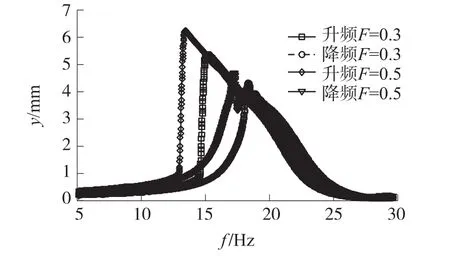
图14 不同激励幅值下的频率响应曲线

6 结论

本文建立非线性双稳态压电振动能量采集器的非线性机电耦合运动方程，并能量采集器非线性振动特性进行了研究分析，仿真和实验验证了本文方法的正确可行性，得到如下结论：①引入非线性磁力模型，线性压电振动能量采集器变成非线性双稳态能量采集器，可以提高能量采集器输出特性；②双稳态压电能量采集器存在三个初始平衡位置；增大激励幅值，可以使非线性双稳态能量采集器经历：小幅值周期振动-多周期振动-拟周期振动-混沌振动-大幅值周期振动；③双稳态压电能量采集器存在跳跃、多解现象；在低频范围内会出现大幅值周期振动，且响应频带很宽；④磁铁间距对系统输出性能影响比较大，当磁铁间距落在［12，16］之间时，系统做大幅值周期振动，出现双稳态振动行为，有利于提高能量采集器的输出性能。

致谢

本文在理论与实验方面受到香港中文大学智能材料与结构实验室的大力支持和指导，在此表示感谢!

［1］Priya S S，Daniel D J.Energy Harvesting Technologies［M］.Springer Sciece+Bussiness Media，LLc，2009.

［2］Harne R L，Wang K W.A Review of the Recent Research on Vi⁃bration Energy Harvesting Via Bistable［J］.Smart Materials and Structures，2013，22：023001.

［3］Sergio P P，Nima T，Mark S，et al.Bistable Vibration Energy Har⁃vester：A Review［J］.Journal of Intelligent Material Systems and Structures，2012，24（11）：1303-1312.

［4］Erturk A，Inman D J.Broadband Piezoelectric Power Generation on High-Energy Orbits of the Bistable Duffing Oscillator with Electromechanical Coupling［J］.Journal of Sound and Vibration，2011，330（10）：2339-2353.

［5］Santon S C，McGehee C C，Mann B P.Nonlinear Dynamics for Broadband Energy Harvesting：Investigation of a Bistable Piezo⁃electric Inertial Generator［J］.Physical D，2010，239（10）：640-653.

［6］Mann B P，Owens B A.Investigations of a Nonlinear Energy Har⁃vester with A Bistable Potential Well［J］.Journal of Sound and Vi⁃bration，2010，329：1215-1226.

［7］Gammaitoni L，Neri I，Vocca H.Nonlinear Oscillators for Vibra⁃tion Energy Harvesting［J］.Applied Physics Letters，2009，94（16）：164102.

［8］Ferrari M，Ferrari V，Guizzetti M，et al.Improved Energy Harvest⁃ing from Wideband Vibrations by Nonlinear Piezoelectric Convert⁃ers［J］.Procedia Chemistry，2009（1）：1203-1206.

［9］孙舒，曹树谦.双稳态压电悬臂梁发电系统的动力学建模及分析［J］.物理学报，2012，61（21）：210505-1.

［10］崔岩，王飞，董维杰，等.非线性压电式能量采集器［J］.光学精密工程，2012，20（12）：2737-2743.

［11］王光庆金文平展永政，等.压电振动能量采集器的力电耦合模型及其功率优化［J］.传感技术学报，2014，26（8）：1092-1100.

［12］展永政，王光庆.双自由度压电振动能量采集器的力-电输出特性分析［J］.振动工程学报，2014，27（6）：871-877.

［13］贾尚帅，孙舒，李明高.基于谐波平衡法的双稳态压电发电系统非线性振动特性研究［J］.振动与冲击，2014，33（6）：170-173.

［14］佘引，温志渝，赵兴强，等.MEMS压电阵列振动能量采集器［J］.传感技术学报，2014，27（8）：1033-1037.

王光庆（1975-），男，博士，教授，主要从事传感检测与信号处理、压电超声驱动器、压电振动能量采集器的理论与应用研究，kele76@163.com；

张 伟（1990-），男，硕士研究生，主要从事压电振动能量采集和压电超声波电机方面的研究工作，510293991@qq.com。

Vibration Performances and Experiments of Nonlinear Piezoelectric Vibration Energy Harvester*

Wang Guangqing1*，Zhang Wei1，Liu Chuang1，Yang Binqiang1，Liao Weihsin2
（1.School of Information and Electronic Engineering，Zhajing Gongshang University，Hangzhou 310018，China；2.Department of Mechanical and Automation，The Chinese University of Hong Kong，Hongkong 999077，China）

In order to improve the output performances of the linear piezoelectric vibration energy harvester（PVEH），a bistable nonlinear PVEH was developed by adding a Duffing nonlinear magnetic force to a tip end of the linear PVEH.The governing motion of the nonlinear electromechanical lumped parameter of the bistable PVEH was derived with considering the dynamic shape and the axial strain of the cantilevered beam of the linear PVEH，a four or five order Runge-Kutta algorithm was used to analyze the dynamic behaviors.The frequency responding function was derived with the resonant balance method；the effects of the exciting frequency，the exciting amplitude and the distance between the two magnets were numerically studied.The research results have shown that the bistable mo⁃tion can not only improve the operating frequency wideband and the energy harvesting efficiency，but also easily make it move in a periodic large-amplitude orbit under a low exciting frequency and amplitude.At last，some experi⁃ments are carried out to testify the validity of the numerical results.

Piezoelectric energy harvester；nonlinear vibration characteristics；bistable behavior；Duffing nonlinear magnetic force

TH825

A

1004-1699(2015)10-1494-09

��2860A

10.3969/j.issn.1004-1699.2015.10.014

项目来源：国家自然科学基金项目（51277165）；浙江省自然科学基金项目（LY15F010001，Y1080037）；浙江省教育厅项目（Y201223050）；浙江工商大学青年人才计划项目（QY11-23）

2015-05-20 修改日期：2015-07-20