评价设计：从结果走向过程

费岭峰+沈强

费岭峰 中学高级教师，浙江省嘉兴市南湖区教育研究培训中心教研员。浙江省优秀教师、浙江省教科研先进个人、嘉兴市名教师、嘉兴市首届“十佳”青年社科人才，浙江省名师培养对象、嘉兴市新世纪专业技术带头人培养人选。曾获全国小学数学教学专业委员会录像课评比一等奖、浙江省“教改之星”金奖，在省级以上专业刊物发表论文或案例145篇。至今主持过省级课题2项，市级课题6项，参与省级课题5项，研究成果和论文曾获市级一等奖以上奖项40次。在市级以上做公开展示交流70余次。经过多年的课堂教学实践与探索，形成了以活动为主线、“活而有效”的小学数学课堂教学特色。

名师慧语：儿童是在成长中的个体，因此都有发展的可能，而教学就是帮助其更主动、更生动发展的重要途径。

我们知道，评价内容的设计往往是引导课堂教学改革的重要因素。对于新课程理念下的小学数学课堂教学而言，其“强调学生对知识发生发展的过程经历，突出数学基本活动经验的形成和数学思维的发展”的目标定位，要在课堂教学中加以落实，产生实效，我们的评价设计就必定也要从“注重结果”的考评走向对“学习过程”的检测，从注重知识记忆式提取与技能的简单重复走向能力的考查与思维水平的评价。唯有如此，才能让小学数学教学走出传统的模式，找到适合新课程理念的方法策略。自2014年起，我们在区域改革项目“促进学生学习力发展的‘绿色评价实践与研究”的带动下，尝试在小学数学学科中实施“能力立意”的测评，取得了一定的经验。现从小学数学“能力立意”测评的设计理念与实践要点方面，谈一些做法与思考。

一、小学数学“能力立意”测评的设计理念

“能力立意”测评，顾名思义是一种着眼于学生能力状况的检测与评价的测评方法。与传统的学科检测相比，“能力立意”的测评体现了三个方面新的设计理念。

1.“能力立意”测评的目标定位，从关注“结果”转向关注“过程”

这是“能力立意”测评与传统检测最基本的区别。《义务教育数学课程标准》（2011年版）在内容目标中提出了“结果目标”与“过程目标”的要求。其意图是在强调，学生通过数学课程的学习，在掌握基础知识、基本技能的同时，更需要在数学的基本思想方法和基本活动经验的形成上有所获得与发展。正因为如此，我们的检测除了要了解学生对基础知识、基本技能的掌握状况之外，更要对学生在基本思想方法和基本活动经验的形成方面作相关的监测与评价。如此，课程目标的实现才能成为现实，对教师教学行为的改进和学生学习行为的改进的指导才能更具有针对性。

2.“能力立意”测评的分析方法，从“量化”分析转向“质性”分析

传统的检测一般以分数的形式来呈现检测结果，很少有对学生在解答习题或解决问题过程中的思维水平或过程优劣作出评定，有时甚至仅仅用一个分数来评定学生的学习能力和学习水平。显然，这样的评定是有失偏颇的，经常会出现“分数较高，能力却并不高”的现象。“能力立意”的测评意在改变这种状况，它在突破传统单一的“量化”设计的基础上，增加了更多“质性”评价的内容。不但重视学生解题结果的呈现，更加重视对学生在解题过程中思维含量的考量与思维水平的评析，由评价者分析被评价者思考过程的“质量”，从而体现新课程理念下更为科学的质量观，为对学生作出更全面的评价创造条件。

3.“能力立意”测评的关注对象，从学生“个体”转向师生“群体”

区域性改革项目“促进学生学习力发展的‘绿色评价实践与研究”的主旨，在于探索“轻负高质”（减轻负担、提高质量）的教育教学实践方式。因此，我们在探索与之相适合的“能力立意”的学科测评方式时，不但关注学生个体的学业成绩与学科素养的提升，同时对教师的教学过程给予关注，拟从测评结果中发现课堂教学存在的问题，从而对教师的课堂教学提出改进建议，或给予直接指导。

二、小学数学“能力立意”测评的实践要点

通过一年多的“能力立意”测评实践，我们在测评材料的选择与编制、测评结果的分析与使用等方面积累了一定的操作经验，现从以下三个方面加以说明。

1.测评材料：以综合性问题为主，突出考查学生的思维过程

传统的检测卷，经常以封闭的习题为主进行设计，目的在于考查学生对基础知识和基本技能的掌握水平，涉及了应用问题，也多以模仿为主，新意不够。我们在“能力立意”测评实践中，除了同样采用少量比较明确的测评点，考查学生对基础知识和基本技能的掌握水平的习题之外，更多地采用了综合性较强，并具有一定开放性的问题，以便检测出学生数学学习的综合水平。具体分为以下几类：

（1）分层递进式问题。所谓分层递进式问题，是指一道习题中包含连续的几个问题，且这几个问题的考查目标是多元的、有层次的，表达形式也是多样的、丰富的。具体又可以细分为两种：

一种是“基础+提升”式问题。此类问题一般由两个问题或三个问题组成，其中有一个问题是基础性的，还有一到两个问题是思维要求比较高的。例如，我们在四年级下学期的“能力立意”测评中，设计了如下一道考查学生对平均数的认识水平的习题。

[例1]小冬和小红参加射击比赛，分别打了5枪，每枪都有得分。

以上问题虽然都是考查学生对平均数的认识与理解，但思维要求是不一样的。第一问是顺向思考，属于基础性的问题。第二问则是逆向思考，学生需要在对平均数是一个虚拟数有了认识和理解的基础之上才能很好地完成，与前一问相比，提高了思维要求。

一种是“结果+说理”式问题。此类问题一般由两部分组成，前一部分是“结果”要求，后一部分则是“思路呈现”要求，所以经常会有诸如“为什么”“你是怎样想的”等追问，以便了解学生解答此题时的思考过程。这样的问题，我们在四年级上学期和下学期的“能力立意”测评中都有涉及。

如四年级上学期考查学生对“公顷”的认识水平的一个问题：

[例2]以下哪个地方的占地面积大约是1公顷？（ ）

A.1个篮球场的面积；B.1间教室的占地面积；C.南湖区的占地面积；D.1个操场的占地面积。

我是这样想的： 。

再如，四年级下学期考查学生对三角形分类知识的理解与掌握水平的一道习题：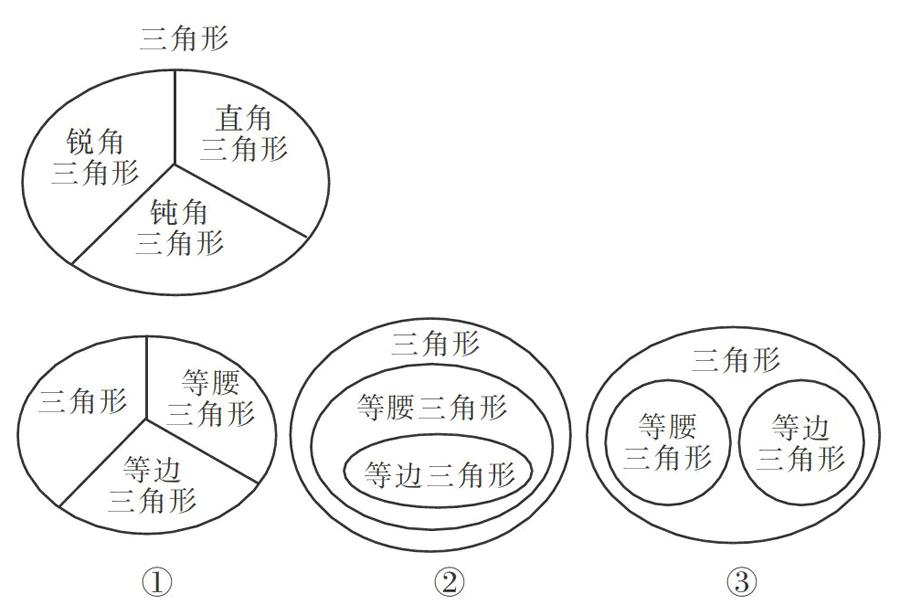

[例3]我们已经知道，三角形按角的特点研究，可以用左图表示。如果我们按边的特点研究，下面第（ ）幅图的表示比较合理。

我的理由是：

以上两个问题便是典型的“结果+说理”式问题。学生在解答此类问题时，答出结果只是完成了问题的一部分，展示思考过程同样重要。

（2）模拟现实的问题。所谓模拟现实的问题，是指问题素材源于生活（有些仅作了少许调整），或者取材于生活情境，或者应用了生活中的真实数据的问题。这些问题一般关注数学与生活的联结，是生活素材稍作加工后的测评材料。如我们在四年级上学期“能力立意”测评时设计的这个问题：

[例4]下图是一张从上海到北京的火车票。这趟火车的平均速度是145千米/小时。李叔叔乘这趟火车于当天16：15到达北京。你能算出上海到北京的距离大约是多少千米吗？

这是学生在学习了“三位数乘两位数”之后设计的一道习题。由于这个问题用了一种很生活化的材料——火车票，与解决问题相关的重要信息隐含在票面上丰富的材料中，需要学生从中读取，既考查了学生从日常生活材料中提取有用信息的能力，又考查了学生结合乘法运算解决实际问题的能力和数学活动经验的形成水平。

（3）突显学法的问题。何谓突显学法的问题？是指考查的目的指向于学生对学习方法的获取水平的问题。这类问题一般是一个新问题，需要学生借助于前期学习中经历过、体验过的学习方法进行解答，从而检测学生对学习方法的掌握水平。

此问题的考查目标，当然是学生在学习了“简便运算”，经历了加法交换律、结合律，乘法交换律、结合律、分配律，以及减法连减、除法连除等运算定律或性质的学习之后，对举例子、不完全归纳法等规律探究方法的经验形成水平。

2.测评分析：分数与分类相结合，注重考量学生的思维水平

“能力立意”测评的设计理念与传统检测很不相同，且在测评材料的选择与设计上更加注重综合性，侧重于“过程目标”与基本思想、基本活动经验。因此，测评分析自然也需要着眼于这些方面。对此，我们重点在两个方面进行了实践与探索。

（1）根据任务完成的程度设定分值。与传统检测的评价相比，“能力立意”测评在给定分值的过程中，不再以唯一结果来给分，而是以任务完成的程度来评定分数。比如，四年级上学期一道检测学生在“大数的认识”中对数概念的认识状况的测试题，我们是这样设计的：

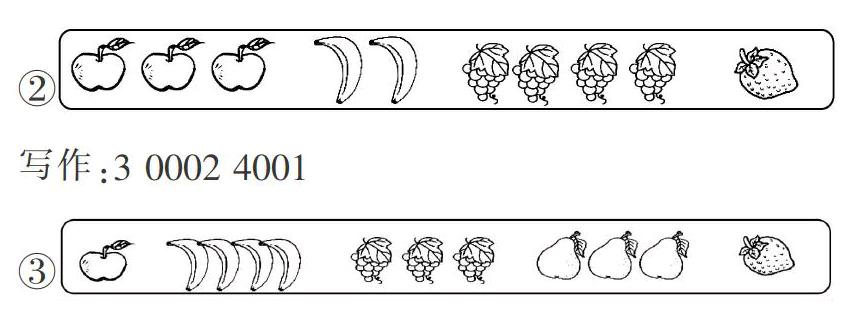
本题考查的内容是“数与代数”领域中“数的认识”的知识。考查目标有两个：一是对数位与计数单位的理解水平，体会两者间的关系；二是经历数位与计数单位的形成过程，积累数的认识经验。正确答案是：1 0004 3301。

在本题的评分过程中，并不是仅仅以“1 0004 3301”这个结果为标准，完全正确才给分，有错就不得分，而是分了四个水平层次设定分值。水平一，对题意不理解，结果完全不正确；水平二：能理解每种水果代表一个数字，并能写出每种水果所表示的数字，写在正确数位上的数字少于一半；水平三，能写出每种水果所表示的数字，写在正确数位上的数字超过一半；水平四，题意理解到位，对每种水果所表示的数字能正确地写在相应的数位上。显然，这样的评分已经不是简单的“要么正确、要么错误”的两分法思路，而是比较清楚地区分了学生在解答此题过程中不同的思维水平。

（2）对结果进行分类处理与解读。“能力立意”的测评不是一个简单的数据收集的过程，它是一个需要对数据进行分析与解读的过程。这也是后续利用测评结果所需要的。

如前文提到的，考查学生对“公顷”认识的问题。测评后，我们进行了两次分类统计，并对学生的说理情况进行了相应的解读。

从统计结果可以看出，选择正确的学生占总人数的66.7%，说明有2/3的学生已经初步建立了“1公顷”的量感。选择“A篮球场”和选择“C南湖区面积”的学生差不多，均超过了一成，显然这些学生对“1公顷”的直接经验的积累还是不够的，所以容易受到相近大小的物体所干扰。

为了对学生的说理情况进行深入了解，我们又对学生进行了第二次分类，完成了以下统计（如下图，人数同上。编码意义：1表示选择错误；2表示选择正确，没有说理或基本说不出来；3表示选择正确，说理不完整或逻辑不清楚；4表示选择正确，说理清楚，符合思维逻辑）。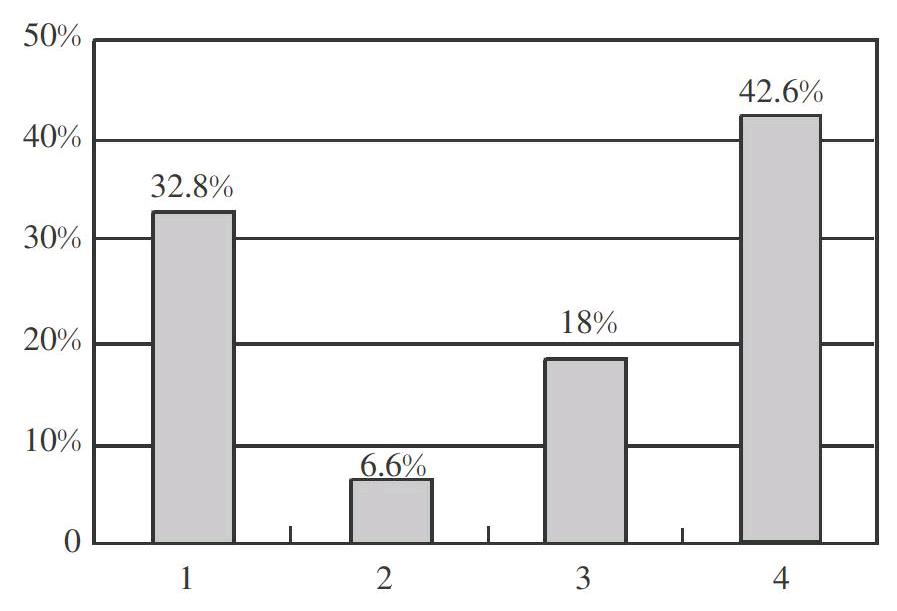

从这个统计结果可以看出，学生呈现思考过程的能力不容乐观。既能正确选择结果，又能完整清楚地表达思考过程的学生不足半数。

最后，对学生的典型答案进行深入分析，完成了第三次分类。从测评结果来看，用“排除法”解答这个问题的学生居多，从意义出发分析思考的较少。这也与学生的思维能力有一定的关系。

3.测评结果：指导教师“教”，帮助学生“学”

“能力立意”的测评，旨在通过了解学生的学习状况，指导教师改进教学，提高教学质量。因此，我们将测评结果，以诊断书的方式反馈至所测班级，在给出每位学生的能力水平等级的基础上，对教学状况作出分析，并提出相应的建议。如四年级上学期测评后，关于“公顷”的教学，我们对几个班教学这节课时的状况进行了调查。从教师的备课资料和访谈中了解到，正确率达到79%的那个班级的任教老师在教学这节内容时，是带着学生到操作场上去观察操作，充分感知1公顷的大小的；其他几个正确率在50%左右的班级则是在教室内完成学习的。由此我们提出建议：如同这样的内容，教学中只需要“走出教室，实地感受，帮助学生建立直接经验，形成表象”即可。

总之，小学数学“能力立意”的测评虽然实践时间不长，但在教师的评价观念和实践操作层面上已经有了很多改进。相信假以时日，将会更加成熟，更加有操作性。?