群与图的对称性

王佳利，王改霞，郑祥

（安徽工业大学数理科学与工程学院，安徽 马鞍山243002）

群与图的对称性

王佳利，王改霞，郑祥

（安徽工业大学数理科学与工程学院，安徽 马鞍山243002）

首先对平面图形的对称进行分析和利用其对称群进行量化，进而将此推广到考察一般图的广义“对称性”与图自同构群的关系，最后刻画了无平方因子阶局部本原弧传递图的自同构群结构.

Cayley图；置换群；局部本原群

1 引言

对称性是自然界很普遍也很重要的特性，自然界中几乎所有重要的规律均与某种对称性有关.要给对称这一概念精确的和一般的描述，特别是对称性在量上的计算，需要利用群论这个工具.群是数学中基本概念之一，群论自19世纪Galois创立以来，不仅成为了近世代数的重要分支，而且其应用范围已深入到科学技术的众多领域，甚至是自然科学的物理、化学、生物的研究中，群论也成为强有力地必不可少的工具.众所周知，关于平面图形的对称性，圆比正方形更对称些；正六边形比正三角形更对称些；正三角形比等腰三角形更对称些等.这些都是直观感性认识.如何去刻画对称性的强弱呢？也就是如何给对称性加以量化？

用运动的观点去看对称，可以把平面图形的对称中用到的运动分为三类：反射（轴对称）、旋转（n次中心对称）和平移（平移对称）.这些运动共同的特点是，都保持平面上任意两点间的距离不变.从而把反射、旋转、平移，或者它们的相继实施，统称为“保距变换”.由上述观点自然的延伸，就可以想到描述平面图形对称性强弱的一种量化的方法.这就是把所有使某平面图形K不变的“运动”放在一起，构成一个集合，记为S（K）并称其为K的对称集.这样就很容易根据S（K）中所含元素个数来进行量化对称性.把保持不变的运动放到一起，构成一个集合，称之为“对称集”，用它来描述的对称性.这个“对称集”不仅仅是一个集合，在这个集合上我们还定义了“保距变换”，并且这种变化还满足一定的运算律，进而构成了一个群.

本文把图形的“对称性”概念加以推广，即一般图形的“点传递性”、“边传递性”和“弧传递”等广义的对称概念，讨论它们的“对称性强弱”，也就是讨论图的自同构群在图上的作用是否“对称”.

2 群与图的对称性的联系

群与图是人们一直关注的两个基本数学对象，各自都有一个庞大的理论体系，但二者结合起来成为一个新的数学领域则是从上个世纪三四十年代开始的.从已知的研究结果可以看出，群论方法在具有较高对称性图的研究中的重要意义确实是其他方法所不能比拟的.图的对称性研究或者说研究某种具有对称性质的图具有重要的理论意义［1-3］.一方面，许多有趣的著名的图都具有某种对称性质，另一方面，对称图与数学的很多方向都有密切的内在联系.

下面用两个例子阐述下群与图对称性之间的联系，即利用图的对称来构造其自同构群以及利用特定群来构造具有某种性质的图类.

2.1利用图的对称性构造群

例2.1设X=（V，E）为一个4个顶点4条边的图，其中

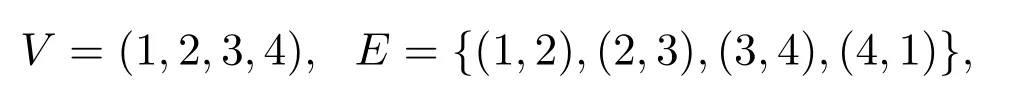
其图示如图1.

图1 四个点四条边的图

根据平面图形的对称性，很容易知道图X有且只有4个轴对称和4个中心对称，它们构成了图自同构群的所有元素，即

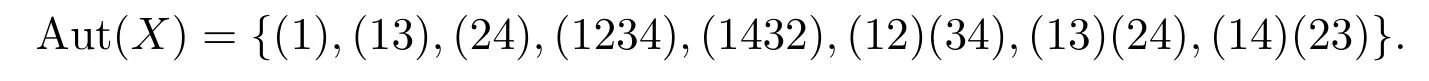
2.2利用群论来构造具有某种对称性的图

Cayley图是由A.Cayley在1878年提出的，当时是为了解释群的生成元和定义关系.但由于它构造的简单性、高度的对称性和品种的多样性，越来越受到图论学者的重视，成为群与图的一个重要的研究领域.近年来，由于计算机的发展，人们发现Cayley图还是构造与设计互连网络的很好地数学模型，因而又获得了实际的应用，它的重要性日益增加.

例2.2令Z3为剩余类加群，S=｛1，2｝为其子集.其所对应的Cayley图图示如下（与图1同构）：

图2 群的Cayley图表示

3 无平方因子阶局部本原图的对称性

给定一个图Γ，用V，E和Arc（Γ）分别表示图Γ的点集、边集和弧集，其中点集的势称作图Γ的阶.设G≤Aut（Γ），若G传递地作用在点集V、边集E或者弧集Arc（Γ）上，则称图Γ分别是G-点传递的、G-边传递的或者G-弧传递的.称图Γ为局部本原图，如果AutΓ的点稳定子在任何一个点邻域上是本原的.本文所指的图均为有限简单连通无向图，未加说明的概念和术语参见文献［4-5］.

从已有文献来看，在图的对称性研究中，无平方因子阶的对称图的刻画和分类已经引起了广泛关注.对于素因子较少的特殊情况已经得到了很好的刻画和分类［6-11］.关于一般情况下无平方因子阶图的对称性方面也有一些有意义的结果［12-16］.特别值得指出的是，文献［1，5］中给出了无平方因子次数的本原置换群的分类结果，这个结果给研究无平方因子阶的图提供了一个很有力的工具.本文下面的定理给出了一个无平方因子阶局部弧传递图及其自同构群的简单刻画.

定理3.1设Γ是无平方因子阶连通k（k/=3）正则G局部本原图，设M是作用在V上至少有三个轨道的最大正规子群且ΓM不是星图，则

（2）Γ是一个奇素数度的二部图，且G同构于D2n：Zk，Zn：Zk，或者（其中k是nk的最小素因子）；

（3）G=M：X，其中soc（X）=T、MT=M×T，且T在V上至多有两个轨道，Γ是T-边传递图.

证明 由于ΓM不是星图，Γ是ΓM的正规覆盖，从而正规子群M在顶点集合V上作用正则.根据M的选择可知，商群G/M在ΓM上作用忠实或者在V ΓM的一个轨道上作用正则，从而存在一个G的一个子群X使得G=M：X.又因为ΓM是G/M局部本原图，所以二元序对（G/M，ΓM）满足G/M的任何一个非平凡的正规子群在ΓM的顶点集至多有两个轨道，从而令Y=soc（X）是X的一个极小正规子群.如果Y=T是不可交换单群，且G/CG（M）是可解的，所以Y≤CG（M），从而MY=M×Y，定理中（3）成立.

下面分下述两种情况来证明定理的前两部分.

情形1Γ≌Kk，k且Y≌T2（T是单群）.

在这种情况下，Y在ΓM的边集上作用传递，从而Y在ΓM上恰好有两个长度为k的轨道，即MY在V上恰好有两个长度为k|M|的轨道.如果Y在ΓM上的每个部分中作用忠实，则T≌A7，k=105，且Tδ≌A6×PSL（3，2），此时很显然ΓM不是X局部传递的.

假设Y在其中一个轨道上作用不忠实，不妨设为UM，令K为Y在ΓM上的核.如果X在VM上作用不传递，则MK/M包含在G/M的一个正规子群中，该正规子群在VM至少有三个轨道.从而G有一个真包含M正规子群且在V上至少有三个轨道，与M的选择矛盾.从而X在VM上作用传递，且Γ是G-弧传递的.很容易证明K≌T在ΓM的另一个分支上传递，令U是UM的MY-轨道.

如果T是非交换单群，因为MK/CMK（M）同构于Aut（M）的一个子群，且是可解的，从

而

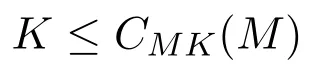
且

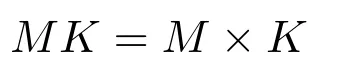
.令∆是包含U的M轨道，根据MK在∆上的作用，可知K在∆上作用是平凡的.故K在VM上作用传递，从而ΓKk，k，M=1，Γ是G弧传递的且G只有一个极小正规子群.定理3.1中（1）成立.

假设T≌Zp（p为奇素数），则k=p与|M|互素，且Aut（ΓM）=（Sp×Sp）：Z2.从而G的Sylow p子群的阶为p2.因为|M|为无平方因子数，所以Out（M）可解.因为Y≌Z2p是X≌G/M的一个极小正规子群，所以G/M是不可交换的.故MMCG（M）.

根据M的选择性，可得MCG（M）在V上至多有两个轨道.即p是|MCG（M）|的一个因子，也是|CG（M）|的一个因子.从而

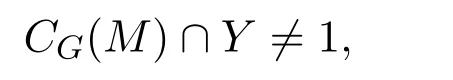
即

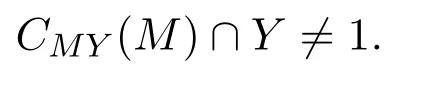
又因为MY和M是G的正规子群，从而CMY（M）是G的正规子群.令P是CMY（M）的Sylow p子群，则CMY（M）=M×P是G的正规子群，从而P是G的正规子群.又由P≤Y，故P=Y.定理3.1中（1）成立.

情形2soc（G/M）≌soc（X）=Y≌Zp，则|VM|=p或者|VM|=2p.

假设CX（Y）=Y，则G=L：Zl，其中l|p-1.所以Gα≌X∆≌Zl或者α∈V，∆是M轨道，则X∆在∆的邻域上作用正则.由于ΓM是X局部本原的，从而|Gα|=k是个奇素数.若G在V上作用不传递，则Gα≌Zk且G≌L：Zk.令q是|L|的素因子满足L的Sylow q子群非正规或者q是|L|的最小素因子，则L有唯一的q′Hall子群N.则N是G的正规子群且N不传递.从而|ΓN|=2q，Γ是ΓN的一个正规覆盖，所以q≥k.如果q＞k，令Q为L的Sylow q子群，有Q≤NCG（N）且NCG（N）=N×Q=L与Q是L的正规子群矛盾.所以q=k.又由于k是|G|的最小素因子，故L≌Zn或者：Zk，即G≌Zn：Zk或假设G在V上作用传递，则G含有一个正规正则子群R=L或者R=L：Z2且Γ≌Cay（R，S），其中S=｛si|0≤i≤k-1｝，s为R中的一个对合.由于|R|是无平方因子数，从而R是一个二面体群，不妨假设R=D2n，则此时D2n：Zk，定理3.1中（2）成立.

假设CX（Y）/=Y，由于X≤（Sp×Sp）：Z2，所以CX（Y）≤Z2p：Z2.又因为X/CX（Y）是Aut（Y）的子群，故X≤（Z2p：Z2）.Zp-1.假设p2不是|CX（Y）|的因子，则|CX（Y）|=Y×K，其中K/=1且K是CX（Y）的p′Hall子群，从而K是X的正规子群且K在VM上作用平凡，从而MK是G的正规子群且与M的轨道相同，从而与M的选择矛盾.从而p2是|CX（Y）|的因子，

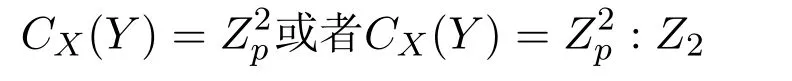
.特别地，ΓM=Kp，p且k=p，此时X在VM上作用传递，Γ是G弧传递图.令Q为CX（Y）的Sylow p子群，则Q是X的正规子群且MQ是G的正规子群.

类似前面的讨论，

如果Q∩CMQ（M）=Q，则M=1且Γ≌Kk，k.如果

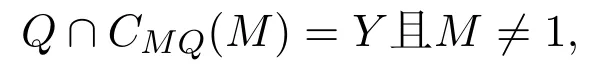
令N是M中指数为素数的正规子群，则NY是G的正规子群.显然，NY在M的两部分都是不传递的，故Γ是ΓNY的一个覆盖.从而soc（G/NY）为素数阶群，Γ是无平方因子阶的二面体群所对应的一个正则Cayley图，定理3.1中（2）成立.

［1］顾沛.对称与群［M］.北京：高等教育出版社，2011.

［2］陈进之.群与图及相关课题的研究［J］.数学理论及应用，2001，21（1）：120-125.

［3］Hahn G，Sabidussi G.Graph Symmetry［M］.The Netherlands：Kluwer Academic Publishers，1996.

［4］徐明曜.有限群导引：上册［M］.北京：科学出版社，1999.

［5］徐明曜，黄建华，李慧陵等.有限群导引：下册［M］.北京：科学出版社，1999.

［6］Chao C Y.The classification of symmetric graphs with a prime number of vertices［J］.Transactions of the American Mathematical Society，1971，158：247-256.

［7］Cheng Y，Oxley J.On weekly symmetric graphs of order twice a prime［J］.Journal of Combinatorial Theory Series B，1987，42：196-211.

［8］Liebeck M W，Saxl J.Primitive permutation groups containing an element of large prime order［J］.Journal of London Mathematical Society，1985，2：237-249.

［9］Marusic D，Scapellato R.Characterizing vertex-transitive pq-graphs with an imprimitive automorphism subgroup［J］.Journal of Graph Theory，1992，16：375-387.

［10］Praeger C E，Xu M Y.Vertex-primitive graphs of order a product of two distinct primes［J］.Journal of Combinatorial Theory Series B，1993，59：245-266.

［11］Praeger C E，Wang R J，Xu M Y.Symmetric graphs of order a product of two distinct primes［J］.Journal of Combinatorial Theory Series B，1993，58：299-318.

［12］Li C H，Maruvsivc D，Morris J.Classifying arc-transitive circulants of square-free order［J］.Journal of Algebraic Combinatorics，2001，14：145-151.

［13］Li C H，Seress A.On Vertex-transitive non-Cayley graphs of square-free order［J］.Designs，Codes and Cryptography，2005，34：265-281.

［14］Li C H，Liu Z，Lu Z P.Tetravalent edge-transitive Cayley graphs of square-free order［J］.Discrete Mathematics，2012，312：1952-1967.

［15］Li C H，Seress A.The primitive permutation groups of square-free degree［J］.Bulletin of the London Mathematical Society，2003，35：635-644.

［16］Li C H，Lu Z P，Wang G X.Vertex-transitive cubic graphs of square-free order［J］.Journal of Graph Theory，2014，75：1-19.

On the group and graph symmetries

Wang Jiali，Wang Gaixia，Zheng xiang

（School of Mathematics and Physics，Anhui University of Technology，Maanshan 243002，China）

In this paper，the symmetries of plane figure is analyzed and quantified at first，then the relation between the general symmetry of a graph and its automorphism group is studied，and the automorphism groups of the locally primitive arc transitive graphs of square-free order is presented.

Cayley graph，Permutation group，Locally primitive

O157.6

A

1008-5513（2015）04-0367-06

10.3969/j.issn.1008-5513.2015.04.005

2015-07-14.

国家自然科学基金（11226276）；安徽省自然科学基金（1408085MA04）；安徽工业大学研究生创新研究基金（2014130）；安徽省大学生创新创业训练项目（AH201310360231，AH201310360341）.

王佳利（1990-），硕士生，研究方向：代数组合，群与图.

王改霞（1982-），博士，讲师，研究方向：代数组合，群与图.

2010 MSC:05C25