二阶离散隐马尔科夫模型的严格定义及等价性质

孙颖华，杨卫国

（江苏大学理学院，江苏 镇江212013）

二阶离散隐马尔科夫模型的严格定义及等价性质

孙颖华，杨卫国

（江苏大学理学院，江苏 镇江212013）

隐马氏模型作为一种具有双重随机过程的统计模型，具有可靠的概率统计理论基础和强有力的数学结构，已被广泛应用于语音识别、生物序列分析、金融数据分析等领域.由于传统的一阶隐马氏模型无法表示更远状态距离间的依赖关系，就可能会忽略很多有用的统计特征，故有人提出二阶隐马氏模型的概念，但此概念并不严格.本文给出二阶离散隐马尔科夫模型的严格定义，并研究了二阶离散隐马尔科夫模型的两个等价性质.

二阶隐马尔科夫模型；观测链；隐藏链

1 引言

在传统的一阶隐马氏模型中存在两个过程，分别是观测过程和状态过程.关于观测过程，假设在给定当前状态的前提下，将来符号的发出概率独立于以前所有的状态和发出的符号；关于状态过程，假设在给定当前状态的前提下，下一步状态的转移概率独立于以前所有的状态和发出的符号.起初一阶隐马氏模型被用于语音识别、模式识别和随机信号方面［1-2］.近年来，研究者们又尝试将其用于生物信息学研究中，如DNA建模、基因检测［3］.2002年，文献［4］对一阶隐马氏模型给出了系统总结.但此类模型无法表示更远状态距离间的依赖关系，就可能会忽略很多有用的统计特征.例如：在文本信息抽取中，简单的一阶隐马氏模型没有考虑上下文特征等信息对抽取性能的作用，也未考虑状态转移概率和观察值输出概率与模型历史状态的关联性；在研究语音信号时，假设各个分段内的各帧语言信号是相互独立的，就会忽略帧与帧之间的相关性；在对生物序列的研究中，待研究的生物序列的残基之间也有很高的相关性，但在此类模型中未涉及.

为了克服一阶隐马氏模型的不足和缺陷，研究者们从不同角度做了改进，提出一些改进措施.其中之一就是考虑状态转移概率和符号发出概率与之前两个状态的依赖关系，提出了二阶隐马尔科夫模型.

文献［5］基于一阶隐马氏模型的状态序列获得了一类二阶隐马氏模型解码问题的Viterbi算法.文献［6］研究了二阶隐马氏模型在语音识别中的应用，为语音识别中的状态延续现象提供一个合理解释，提高了识别效果.文献［7］系统研究了二阶隐马氏模型三个基本问题算法，并研究了与一阶隐马氏模型之间的关系，并给出等价性定理.文献［8］在传统的隐马氏模型的基础上，研究改进了Baum-Welch算法，并导出了改进模型的参数估计公式.文献［9］利用二阶隐马氏模型研究时空数据挖掘问题，表明二阶隐马氏模型对平稳段定位具有非常好的性能.文献［10］提出了基于二阶隐马氏模型的文本信息抽取算法，分析了其在文本信息抽取中的有效性，最终证得新算法提高了抽取精度.文献［11］提出了基于二阶隐马尔可夫模型，表明新模型较传统的模型有更高的词性标注正确率和消歧率.文献［12］研究了二阶隐马氏模型的基本算法，将二阶隐马氏模型（second-order hidden markov model，简记为HMM2）应用到microRNA（miRNA）靶基因预测的后期过滤处理中，也取得较好效果.文献［13］就高阶隐马尔可夫模型算法基础中的EM算法（expectation-maximization algorithm）和动态规划进行了一定梳理分析，从而促进高阶隐马氏模型在实际中的应用.

目前，二阶隐马尔科夫模型已被广泛的应用，但还未发现其严格定义.在本文中，仿照文献［4］中的一阶隐马氏模型的严格定义，给出二阶离散隐马氏模型的严格定义并研究了二阶离散隐马氏模型的两个等价性质.

2 定义

定义2.1设S=｛1，2，···，N｝，L=｛1，2，···，M｝为两有限状态空间，X=｛Xn，n≥0｝，Y=｛Yn，n≥0｝是分别在S与L上取值的随机变量序列.如果X=｛Xn，n≥0｝为二阶隐马氏链，其二维初始分布与二阶转移矩阵分别为：

则称｛X，Y｝=｛Xn，Yn，n≥0｝是二阶隐马尔科夫模型.X=｛Xn，n≥0｝被称为二阶隐马氏模型的隐藏链，Y=｛Yn，n≥0｝被称为二阶隐马氏模型的观测链.

3 主要结果

在给出二阶离散隐马尔科夫模型的严格定义后，本节研究二阶离散隐马氏模型的两个等价性质.

引理3.1设X=｛Xn，n≥0｝与Y=｛Yn，n≥0｝是分别在S与L上取值的随机变量序列，则（3）式成立的充要条件是：对任意n≥1，有

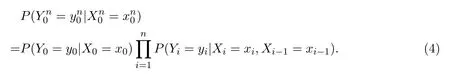
定理3.1设X=｛Xn，n≥0｝，Y=｛Yn，n≥0｝如前定义，则｛X，Y｝=｛Xn，Yn，n≥0｝为由定义1.1定义的二阶隐马尔科夫模型的充要条件是：∀n≥1，

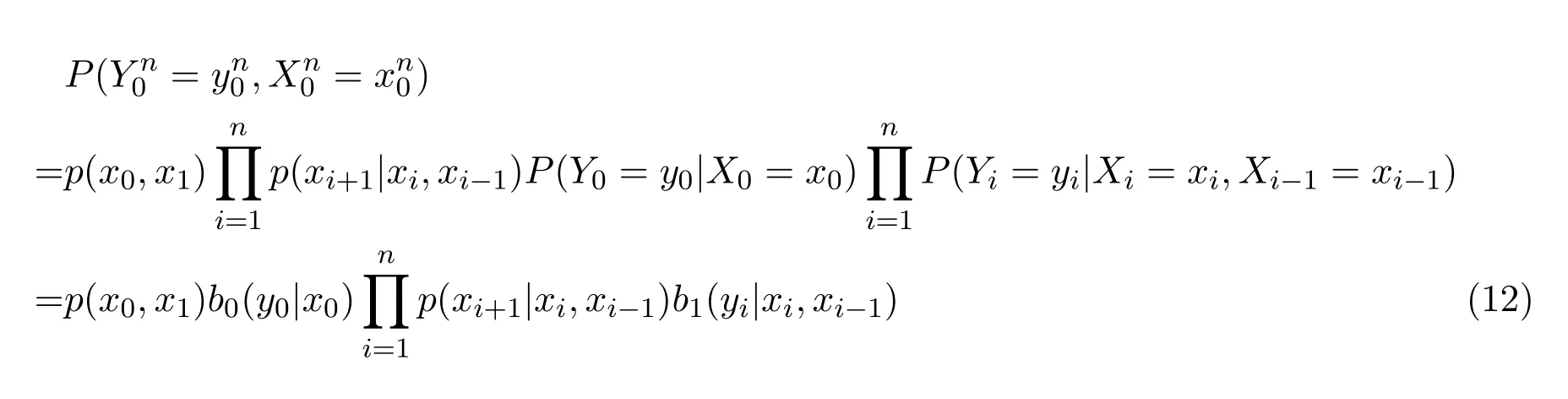
证明 由引理及二阶马氏链的等价性，可得本定理成立.

注3.1由公式（12）可得到文献［15］中公式（6）.

定理3.2设X=｛Xn，n≥0｝，Y=｛Yn，n≥0｝如前定义，则｛X，Y｝=｛Xn，Yn，n≥0｝为由定义1.1定义的二阶隐马尔科夫模型的充要条件是：∀n≥2，

注3.2公式（13）与公式（14）即为文献［15］中公式（5）与公式（4）在m=2，n=2时的情形.

［1］Levinson S E.Structual methods in automatic speech recognition［J］.Proceeding of the IEEE，1985，73：1625-1650.

［2］Rabiner L R.A tutorial on hidden markov models and selected applications in speech recognition［J］. Proceeding of the IEEE，1989，77（2）：257-286.

［3］王翼飞，史定华.生物信息学-智能化算法及其应用［M］.北京：化学工业出版社，2006.

［4］Ephraim Y，Merhav N.Hidden Markov process［J］.IEEE Transactions on Information Theory，2002，48（6）：1518-1569.

［5］He Y.Extended Viterbi algorithm for second order hidden Markov process［J］.IEEE 9th International Conference on Pattern Recognition，1988，2：718-720.

［6］Mari J F，Haton J P，Kriouile A.Automatic word recognition based on second-order hidden Markov models［J］.IEEE Trans.Speech Audio Processing，1997，5（1）：22-25.

［7］史笑兴，王太君，何振亚.二阶隐马尔科夫模型的学习算法及其与一阶隐马尔科夫模型的关系［J］.应用科学学报，2001，19（1）：29-32.

［8］杜世平，李海.二阶隐马尔可夫模型及其在计算语言学中的应用［J］.四川大学学报，2004，41（2）：284-289.

［9］Mari J F，Le Ber F.Temporal and spatial data mining with second-order hidden Markov models［J］.Soft Computing，2006，10（5）：406-414.

［10］周顺先，林亚平，王耀南，等.基于二阶隐马尔可夫模型的文本信息抽取［J］.电子学报，2007，35（11）：2226-2231.

［11］刘洁彬，宋茂强，赵方，等.基于上下文的二阶隐马尔可夫模型［J］.计算机工程，2010，36（10）：231-235.

［12］高松，秦殿刚，冯铁男，等.二阶HMM算法改进及在miRNA靶基因预测中的应用［J］.应用科学学报，2010，28（3）：307-312.

［13］叶飞.隐马尔可夫模型算法基础探析［J］.铜陵学院学报，2014，3：108-112.

［14］Chung K L.A Course in Probability Theory［M］.London：Academic Press，2010.

［15］叶飞，王翼飞.高阶隐马氏模型研究进展［J］.数学进展，2014，43（2）：219-231.

The strict definition of second-order discrete hidden Markov model and its equivalent nature

Sun Yinghua，Yang Weiguo

（Faculty of Science，Jiangsu University，Zhenjiang212013，China）

Hidden Markov model，as a statistical model of doubly stochastic process，has a reliable theoretical foundation in probability and statistics and strong mathematical structure.It has been widely used in speech recognition，biological sequence analysis，financial data analysis，etc.As the conventional first-order hidden Markov model can not express the dependency relationship between the further distance，many useful statistical characteristic were ignored in many works.Therefore，the concept of second-order hidden Markov model was put forward，but this concept is not strict.In this paper，we give the strict definition of second-order discrete hidden Markov model and study two equivalent properties of the second-order discrete hidden Markov model.

second-order hidden Markov model，observation chain，hidden chain

O211.62

A

1008-5513（2015）04-0380-07

10.3969/j.issn.1008-5513.2015.04.007

2015-04-07.

国家自然科学基金（11071104）.

孙颖华（1991-），硕士生，研究方向：隐马尔科夫模型.

2010 MSC:60J05