MHD flow of a visco-elastic fluid through a porous medium between infinite parallel plates with time dependent suction*

BAAG S.， ACHARYA M. R.， DASH G. C.， MISHRA S. R.

1. Department of Physics， College of Basic Science and Humanities， OUAT， Bhubaneswar-751003， India，E-mail: sbaag22@gmail.com

2. Department of Mathematics， ITER， SOA University， Bhubaneswar-751030， India

MHD flow of a visco-elastic fluid through a porous medium between infinite parallel plates with time dependent suction*

BAAG S.1*， ACHARYA M. R.1， DASH G. C.2， MISHRA S. R.2

1. Department of Physics， College of Basic Science and Humanities， OUAT， Bhubaneswar-751003， India，E-mail: sbaag22@gmail.com

2. Department of Mathematics， ITER， SOA University， Bhubaneswar-751030， India

2015，27（5）:738-747

This work provides a comprehensive theoretical analysis of MHD unsteady free convection viscoelastic fluid flow through a porous medium. The medium is treated as incompressible and optically transparent. The flow of the fluid is initiated by shearing action of the moving wall with time dependent suction. Radiative heat flow is considered in temperature equation. The coupled nonlinear problem has been solved asymptotically. Approximate solutions have been obtained for the mean velocity， mean temperature using multi parameter perturbation technique. The originality of the present study is to investigate the effect of viscoelastic property of the fluid （WaltersB′model） on the flow and heat transfer phenomena when the flow is permeated through a porous medium with uniform porous matrix subject to transverse magnetic field and time dependent fluctuative suction at the boundary surface. The case of viscous flow has been discussed as a particular case on comparison with the result reported earlier and it is in good agreement. Flow reversal is indicated incase of viscoelastic fluid with high heat capacity in the presence of magnetic field. The higher cooling of the plate in case of viscoelastic flow also causes a flow reversal.

viscoelastic liquid， porosity， radiation parameter， time dependent suction

Introduction

Numerous applications of viscoelastic fluid in several manufacturing processes have led scientist to investigate viscoelastic boundary layer flow. The boundary layer analysis of idealized viscoelastic fluid was introduced by Beard and Walters［1］. Subsequently great interest has been shown in the investigation of natural convection of heat transfer of viscoelastic fluid. An extensive range of physical models has been developed to stimulate the diverse hydrodynamic behavior of viscoelastic （non-Newtonian） fluid. Viscoelastic fluid flow through porous media has received special attention because of increasing practical application in oil reservoir technology. The oil displacement efficiency may be improved by using non-Newtonian fluids. In view of above application， it is justified to have an adequate understanding of the flow behavior of viscoelastic fluids. Literature has witnessed a number of studies in this matter. Recent studies include the work of Choudhury and Islam［2］. They studied MHD free convection flow of viscoelastic fluid past an infinite vertical porous plate.

Abel et al.［3］have reported viscoelastic fluid flow and heat transfer over stretching sheet with variable viscosity. Later on Asghar et al.［4］studied the flow of non-Newtonian fluid induced due to oscillation of a porous plate. Stretching of porous plate is also another important aspect. Viscoelastic boundary layer MHD flows over a porous quadratic stretching sheet have been reported by Khan and Sanjayanand［5］. Khan［6］considered radiation effect on heat transfer in a viscoelastic fluid flow over a stretching surface. By using Darcy’s law Yamamoto and Yoshida［7］considered suction and injection flow with convective acceleration through a plane porous wall. Chawla and Singh［8］studied oscillatory flow past a porous bed. The steady two-dimensional free convective flow of a viscous fluid through a porous medium bounded by a porous surface subjected to a constant suction velocity wasstudied by Raptis et al.［9］.

Singh et al.［10］discussed the oscillatory suction velocity in presence of time dependent viscosity along magnetic field. Ferdows et al.［11］analyzed free convection flow with variable suction in presence of thermal radiation. Mishra et al.［12］have studied MHD flow of a viscoelastic fluid through porous medium with oscillatory suction.

In many instances coal slurries exhibit non-Newtonian characteristics. This is an integral part of coal based fuel production with low pollutants. This led Massoudi and Phuoe［13］to study unsteady motion of nonlinear viscoelastic fluid. A review article on single phase flow of non Newtonian fluids in porous media was addressed by Sochi［14］. In this article the flow through porous media in general are examined. Alharbi et al.［15］considered chemical reaction in heat and mass transfer of a MHD viscoelastic fluid flow. Kumar et al.［16］discussed unsteady motion in their research. Attempt was made by Sivraj et al.［17］to solve viscoelastic fluid flow in irregular channel. Recently，a visco-elastic fluid model known as Phan-Thien-Tanner （PTT） model［18］is widely used for wire coating.

In the present work an attempt has been made to study MHD free convection flow of viscoelastic fluid（WaltersB′model） with time dependent suction in presence of radiative heat transfer through a porous medium. In the physical model the plate at y =0is at very high temperature Twand the plate at y=h is at a temperature T∞such that Tw≫T∞. The originality of the present study is to investigate the effect of viscoelastic property of the fluid （Walters B′model）on the flow and heat transfer phenomena when the flow is permeated through a porous medium with uniform porous matrix subject to transverse magnetic field and time dependent fluctuative suction at the boundary surface. The case of viscous flow has been discussed as a particular case in comparison with the result reported earlier and it is in good agreement with the present one.

The present study is of great importance in the movement of oil， gas and water through the reservoir of an oil or gas to the hydrologist in his study of the migration of underground water， and to the chemical engineer in connection with filtration processes. Beyond this， the study is widely applicable in soil mechanics， water purification， ceramic engineering and powder metallurgy. The results of the problem are also of great interest in geophysics in the study of the interaction of the geomagnetic field with the fluid in geothermal region. Water in the geothermal region is an electrical-conducting liquid because of high temperature. With the fuel crisis deepening all over the developed world， attention is turning to the utilization of the enormous power beneath the Earth’s crust in the geothermal region.

The analytical solutions for the velocity field and temperature distribution are obtained by perturbation technique. The effect of the flow parameters on the velocity field and temperature distribution are presented with the aid of graphs.

1. Mathematical formulation

Free convection flow of an electrically conducting viscoelastic fluid between infinite vertical parallel porous plates with time dependent suction has been considered. The flow of the fluid is initiated by the shearing action of the moving wall with resulting suction and small pressure gradients along the direction of motion （see Fig.1）. A magnetic field of uniform strength B0is applied normal to the plate. The induced magnetic field is neglected as the magnetic Reynolds number of the flow is taken to be very small. All the fluid properties are constant and the influence of density variation with temperature is considered only in the body force term. The flow is assumed to be in thex′direction， which is along the vertical plate in the upward direction and y′-axis is taken to be normal to the plate. The moving electric field is produced due to flow of electrically conducting viscoelastic fluid in a magnetic field which produces a current called the conduction current. We have assumed the magnetic field diffuses easily through the medium and when the condition is violated the Hall current is produced. Therefore， we have neglected Hall current. We have considered Darcian model to account for the permeability of the medium.

Following Hassanien［19］for unsteady two dimensional flow of a viscous and electrically conducting fluid through a porous medium and free convection flow Alagoa et al.［20］the governing equations for above flow are

such that εA=1

Fig.1 Flow geometry

The terms of Eq.（3） for two dimensional boundary layer equations for flow over plane wall are of orderandand henc［1e9］Eq.（3） has not［20］been considered，Hassanien and Alagoa et al.. WhereA is the small positive parameter，g is the acceleration due to gravity，ε is the small positive number，βis the volumetric expansion coefficient for thermal expansion，T′is the fluid temperature，k0is the rotational viscosity component，kpis the permeability parameter，αis the absorption coefficient. The radiative heat flux equation for an optically thin environment（α≪1） such as intergalactic layers for which plasma gas is assumed to be of low density is given by

where T∞denotes temperature at equilibrium. Substituting Eq.（5） in Eq.（4）， we have

The corresponding boundary conditions are

whereh is the characteristic width of the channel，k is the thermal conductivity，cpis the specific heat，σ is the electrical conductivity and Re=v0h/n， suction Reynolds number. Introducing new variables in the non dimensional form as

where u0and v0are the mean velocities ofu′and non-zero constant suction velocityv′.n is the kinematic viscosity （=µ/ρ），µis the dynamic viscosity，ρis the density of fluid. Substituting Eq.（1） in Eqs.（2）and （6） and introducing new variables given in Eq.（8）as well as dropping the dashes， we find

where

On introducing the non dimensional variables given in Eqs.（8）， boundary conditions given in Eqs.（7） reduce to

where χ2is the dimensionless porosity parameter，M2is the non dimensional magnetic parameter，is the Grashof number，Rcis the visco-elastic parameter，Pr is the Prandtl number，θis the dimensionless temperature，N2is the radiation parameter.

2. Method of solution

Equations （9） and （10） representing the flow variables are highly non-linear. So solutions to these non-linear equations are obtained by perturbation method. The parameters Rc，ε andA are assumedsmall such that Rc≪1andε≪1. Velocity and temperature in the neighborhood of the plate can be expressed as:

where u0and θ0are the mean velocity and mean temperature respectively. Using Eqs.（13） and （14） in third order differential Eq.（9）， equating harmonic and non-harmonic terms for mean velocity and mean temperature， after neglecting coefficient ofε2， we get

with corresponding boundary conditions

and

with corresponding boundary conditions

Equations （15） and （18） are third order differential equations due to presence of viscoelastic parameter. There are only two boundary conditions. Therefore， it needs one boundary condition more for unique solution. Thus， to avoid this difficulty， we adopt perturbation method. Here u0and u1are expanded following Beard and Walters［1］.

Substituting Eq.（21） in Eq.（15） and equating coefficients of zeroth order and first order of Rcwe get

The corresponding boundary conditions are

Substituting Eq.（21） in Eq.（15） and equating coefficients of zeroth order and first order of Rc

The corresponding boundary conditions are

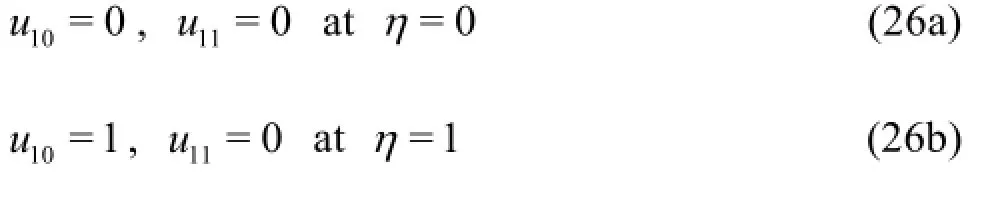
Solution of these equations for the flow variables are obtained starting with the temperature in Eq.（16）. Assuming that the temperature difference between the plate at y=0and its neighbouring point is small， the temperatureθ0can be expanded following Bestmann［21］as

whereψis the small correction factor such that O（θw）＜ψ＜O（1）.

Neglecting squares and products ofψ， Eq.（15）becomes

where

3. Results and discussion

In this paper the MHD boundary layer problem for momentum and heat transfer with thermal radiation in viscoelastic fluid flow through a channel embedded in a porous medium is investigated. In order to verify the accuracy we have compared our results with the results of previous authors. During the discussion we have considered the real part of the solution unless it is mentioned otherwise. The value of ε=0.01.

Fig.2 Effect of M ，Pr and Rcon velocity profile （Gr=5，N2=5，χ2=10，ωT=π/2）

Figure 2 displays the velocity variation for various values ofPr，M and Rcfor fixed values of Gr=5，N2=5，χ2=10，ωt=π/2. It is seen that the velocity increases almost exponentially from zero at the lower wall to unity at the upper wall. Further， it is seen that the elasticity property of the fluid（Rc= 0.2） in the presence of magnetic field causes a decrease in the velocity at all points. Moreover， higher Prandtl number fluid also decreases the velocity at all points. One remarkable finding is that when a higher Prandtl number （fluid with higher heat capacity） viscoelastic fluid is subjected to magnetic field a flow reversal is indicated.

Fig.3 Effect of χ2，M andPr on velocity profile （G=5，r N2=5，ωT=π/2）

Therefore， the present study suggests that a right choice of viscoelastic fluid with a controlled magnetic field strength prevents the flow reversal in the flow domain. On a careful analysis it is further revealedthat Prandtl number is a salient characteristic number based upon pure physical property （Pr=µcp/k） whereasis a resistive force of electromagnetic origin， acting along the main direction of the flow perpendicular to the direction of the magnetic field which decreases in the proportion to square of the suction velocity and elastic parameter Rc，（Rc=）which grows in proportion to square of the suction velocity. The same observation in respect of magnetic parameter and Prandtl number was observed by［19］in the study of MHD flow through a porous medium.

Figure 3 depicts a two layer velocity profile due to high （χ2=10）and low （χ2=5）value of suction Reynolds number. High suction Reynolds number implies larger suction velocity （Re=v0h/n）. As χ2is inversely proportional to square ofRe ， the higher value of χ2implies low suction velocity. It is clear that for low suction velocity has a thinning effect over the boundary layer thickness and it is further reduced by higher Prandtl number and magnetic parameter. The special feature of the high χ2velocity profiles is that it steadily increases whereas for low value， it increases and slightly decreases near the upper plate. Thus， it is inferred that low suction has a decelerating effect near the permeable surface. The crossing of curves IV and VI in Fig.3 may be attributed to the interplay of Prandtl number and magnetic effects.

Fig.4 Mean velocity profile with M =2，Rc=0.2

Figure 4 primarily exhibits the effect of Grashof number and radiation parameter （N2）for cooling and heating of the plate. It is evident from curves II and VI，one for heating （Gr＞0）and other for cooling （Gr＜0） that the heating of the fluid exerts greater buoyancy force which accelerates the fluid motion and cooling acts adversely resulting a flow reversal in the presence of elasticity of the fluid. The flow reversal increases with higher value of Gr＜0. The instability of the flow may be attributed to the non linearity in the constitutive equations. The flow reversal increases with higher Gr＜0. These instabilities may not depend on inertia， they are mainly driven by the fluid normal stresses （elasticity）， or by the boundary conditions［19］. Further it is seen that an increase in radiation parameter N2is to reduce the velocity throughout the flow field. This observation coincides with the work of Alagoa et al.［20］.

Fig.5 Effect of Rc，ωandt on velocity profile （Pr =0.71，N2=0.5，χ2=10，M =2，Gr=5）

Fig.6 Effect ofPrand N2on temperature profile

From Fig.5 it is seen that there is no significant variation in velocity due to variation in the values of ω， the frequency or timet as the physical property of the fluid such as elasticity associated in the flow phenomena overrides their effects.

Figure 6 displays the temperature variation in thermal boundary layer. This two layer profile is mainly due t o hig her va lues ofPr an d lower v alues of Pr . Thenonlineardistributionisattributedduetohigher value of Pralso. The contribution of the radiation parameterN2is to increase the thermal boundary layer thickness preserving the linearity of the distribution. Equation （16） represents the steady temperature distribution. In the absence of radiation parameter（N2=0）this reduces to a simple equation for temperature distribution which varies exponentially with respect to Prandtl number which is comparable to the classical property of fluid temperature distribution.

Table 1 shows the variation of skin friction coefficient， a measure of boundary phenomena coefficient，with phase angleωtand other pertinent parameters. It is observed that an increase in phase fromπ/4to π/2for a viscous fluid （Rc=0）， skin friction decreases slightly but in case of viscoelastic fluid this decrease is significant. It is further noticed that when Rc， the elastic parameter， increases from 0.2 to 0.4 the skin friction reduces to negligibly small. This result infers that an increase in phase angle as well as elastic parameter is found to be favorable in reducing the skin friction significantly which is desirable for streamline flow. The decrease in skin friction is also noted due to the presence of porous medium as well as increase in magnetic parameter and radiation parameter. All the above results hold good for a heated plate（Gr＞0）. One interesting result is that for a cooled plate（Gr＜0）， a negative value of skin friction is recorded. This observation is important in view of flow reversal. This fact is concomitant with the observation made from Fig.3 curve VI， for （Gr＜0）indicating a flow reversal.

Table 1 Skin friction coefficient

Table 2 presents the variation of Nusselt numberNu. It is seen that an increase in radiation parameter and suction parameter increasesNuslightly but the reverse effect is marked in case of Prandtl number. It is further noticed that phase change has no significant contribution in the variation of Nusselt number.

Table 2 Nusselt number

4. Conclusion

Flow reversal is indicated incase of viscoelastic fluid with high heat capacity in the presence of magnetic field. The higher cooling of the plate in case of viscoelastic flow also causes a flow reversal. The non linearity of temperature distribution is concomitant with higher heat capacity of the fluid i.e.， higherPr and the increasing radiation contributes to linearity. Increase in phase angle as well as elastic parameter isfound to be favorable in reducing the skin friction significantly in case of heated plate. For a cooled plate，negative skin friction is recorded. Suction parameter slightly increases the Nusselt number.

Acknowledgement

Authors express their deepest sense of gratitude to the authorities of SOA University for providing facilities to carry on the research work and thankful to the reviewers for the constructive comments.

References

［1］ BEARD D. W.， WALTERS K. Elastico-viscous boundary layer flow. Two dimensional flow near a stagnation point［J］. Proceedings of the Cambridge Philosophical Society， 1964， 60（3）: 667-674.

［2］ CHOWDHURY M. K.， ISLAM M. N. MHD free convection flow of viscoelastic fluid past an infinite vertival porous plate［J］. Heat and Mass Transfer， 2000，36（5）: 439-447.

［3］ ABEL M. S.， KHAN S. K. and PRASAD K. V. Study of viscoelastic fluid flow and heat transfer over a stretching sheet with variable viscosity［J］. International Journal of Non-Linear Mechanics， 2002， 37（1）: 81-88.

［4］ ASGHAR S.， MOHYUDDIN M. R. and HAYAT T. et al. The flow of non-Newtonian fluid induced due to oscillation of a porous plate［J］. Mathematical Problems in Engineering， 2004， 2: 133-143.

［5］ KHAN S. K.， SANJAYANAND E. Viscoelastic boundary layer MHD flow through a porous medium over a porous quadratic stretching sheet［J］. Archives of Mechanics， 2004， 56（3）: 191-204.

［6］ KHAN S. K. Heat transfer in viscoelastic fluid flow over a stretching surface with heat source/sink， suction/ blowing and radiation［J］. International Journal of Heat and Mass transfer， 2006， 49（3）: 628-639.

［7］ YAMAMOTO K.， YOSHIDA Z. Suction and injection flow with convective acceleration through porous wall［J］. Journal of the Physical Society of Japan，1974， 37（3）: 774-779.

［8］ CHAWLA S. S.， SINGH S. Oscillatory flow past a porous bed［J］. Acta Mechanics， 1979， 34（3-4）: 205-213.

［9］ RAPTIS A.， PEREDIKIS C. and TZIVANIDIS G. Free convection flow through a porous medium bounded by a vertical surface［J］. Journal of Physics D Applied Physics， 1981， 14（7）: L99-L102.

［10］ SINGH A. K.， SINGH A. K. and SINGH N. P. Heat and mass transfer in MHD flow of a viscous fluid past a vertical plate under oscillatory suction velocity［J］. Indian Journal of Pure and Applied Mathematics，2003， 34（3）: 429-442.

［11］ FERDOWS M.， SATTAR M. A. and SIDDIQUI M. N. A. Numerical approach on parameters of the thermal radiation interaction with convection in boundary layer flow at a vertical［J］. Thammasat International Journal of Non-Linear Mechanics， 2004， 9（3）: 19-23.

［12］ MISHRA S. R.， DASH G. C. and ACHARYA M. Mass and heat transfer effect on MHD flow of a visco-elastic fluid through porous medium with oscillatory suction and heat source［J］. International Journal of Heat and Mass Transfer， 2013， 57（2）: 433-438..

［13］ MASSOUDI M.， PHUOE T. X. Unsteady motion of a non-linear viscoelastic fluid［J］. International Journal of Non-Linear Mechanics， 2009， 44（10）: 1063-1072.

［14］ SOCHI T. Non-Newtonian flow in porous media［J］. Polymer， 2010， 51（22）: 5007-5023.

［15］ ALHARBI S.， BAZID M. and GENDY M. Heat and mass transfer in MHD visco-elastic fluid flow through a porous medium over a stretching sheet with chemical reaction［J］. Applied Mathematics， 2010， 1（6）: 446-455.

［16］ KUMAR J. G.， SATYANARAYAN P. V. Mass transfer effect on MHD unsteady free convective Walters memory flow with constant suction and heat sink［J］. International Journal of Applied Mathematics and Mechanics， 2011， 7（19）: 97-109.

［17］ SIVRAJ R.， RUSHI KUMAR B. Unsteady MHD dusty visco-elastic fluid Couette flow in an irregular channel with varying mass diffusion［J］. International Journal of Heat and Mass Transfer， 2012， 55（11-12）: 3076-3089.

［18］ Nhan-Phan-Thein. Understanding viscoelasticity. An introduction to Rheology［M］. 2nd Edition， Berlin，Germany， Springer.

［19］ HASSANIEN I. A. Unsteady hydromagnetic flow through a porous medium between two infinite parallel porous plates with time varying suction［J］. Astrophysucs and Space Science， 1991， 175（1）: 135-147.

［20］ ALAGOA K. D.， TAY G. and ABBEY T. M. Radiative and free convective effects of a MHD flow through a porous medium between infinite parallel plates with time dependent suction［J］. Astrophysics and Space Science， 1998， 260: 455-468.

［21］ BESTMANN A. R. Free convection effects on the flow past a vertical porous plate set impulsively into motion with negligible dissipation［J］. Acta Physical Academiae Scientiarum Hungaricae， 1979， 46（3）: 129-136.

Appendix

The following are the constants that appear in Eqs.（26）， （27）， （29）， （30）.

10.1016/S1001-6058（15）60536-4

（December 15， 2013， Revised May 20， 2014）

* Biography: BAAG S. （1976-）， Female， Ph. D.，Assistant Professor