项目投资选择模型的左右得分型TOPSIS法

李兰平

(湖南财政经济学院 基础课部,长沙 410205)

项目投资选择模型的左右得分型TOPSIS法

李兰平

(湖南财政经济学院 基础课部,长沙 410205)

由于决策者知识的局限性和现实决策问题的复杂性，某些多属性决策问题的属性值常需要模糊数刻画。三角模糊数是一类有效刻画模糊属性值的一类模糊数，于是针对属性值为三角模糊数的项目投资选择问题，提出了一类新的多属性决策方法。其具体步骤是：首先利用左右得分的基本思想将规范化的三角模糊数定义左右得分，进而将决策矩阵转化为基于得分的区间数决策矩阵，最后依据TOPSIS法的基本思想对备选方案进行排序和择优。文末通过实际例子说明本文所提出的方法的有效性和实用性。

多属性决策；三角模糊数；左右得分；TOPSIS法

在经济全球化的推动下,企业间的竞争也来越激烈,决策者遇到的决策问题也变得越来越复杂。然而由于决策者的知识的局限性以及人类认识世界的不完全性,很多方案的评价(属性)值是很难用精确数的形式给出的,即使勉强用精确数进行描述也会损失一些信息影响到决策结果的有效性。针对上面的问题,很多模糊多属性决策方法被提出并已经成为管理决策的热点,其应用领域已经应用到诸如投资伙伴选择、教师绩效评价、旅游出行方案选择等人类生活的各个方面。由于三角模糊数在刻画模糊性的优势,针对属性值为三角模糊数的多属性决策问题得到了很多学者的关注和研究。文献[1]针对属性值以及决策者的偏好均为三角模糊数的多属性决策问题,提出了基于相似度的多属性决策方法;文献[2]给出了考虑决策者的多维偏好的三角模糊数型多属性决策法;文献[3]针对属性值及属性权重均以模糊语言形式给出的多属性群决策问题,通过引入方案间的优势度和优势度比较矩阵,先将语言信息转化为三角模糊数,然后提出了基于理想点权值的多属性决策方法;文献[4]针对属性值及属性权重为模糊语言形式的多属性群决策问题,先将语言信息转化为三角模糊数,通过构造集结决策者权威性和意见一致性的组合一致性指数,提出了一种模糊多属性群决策算法;文献[5]针对属性值为三角模糊数的多属性决策问题,提出了一种基于模糊信息的熵权多属性方案评估方法;文献[6]针对属性权重完全未知且属性值为三角模糊数型多属性决策问题,提出一种基于线性规划和模糊向量投影的决策方法;文献[7]将三角模糊数应用到我国博士后科研成果评价研究,建立了完整的博士后科研成果评价体系;文献[8]提出了去模糊化的最大最小法,该法首先通过定义三角模糊数排序的左右得分然后提出了基于左右得分的效用函数排序法对三角模糊数进行排序.本文将基于其左右得分的思想通过将三角模糊数决策矩阵转化为区间数决策矩阵,进而针对项目投资选择问题提出一种新的三角模糊数型多属性决策法。

1 预备知识

定义1 若三角模糊数~A的隶属度函数定义为

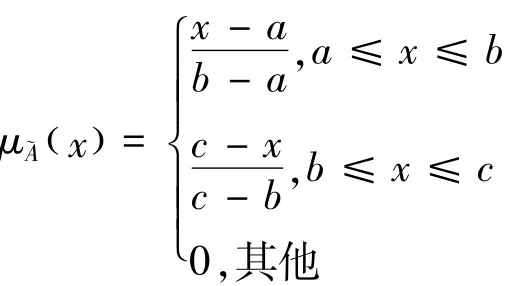
对于某一多属性决策问题,设X=｛x1,x2,…,xm｝是方案集,O=｛o1,o2,…,on｝是属性集。给出了方案xj在属性oi下的属性值为三角模糊数),并设相应的属性权重向量为w =(w1,w2,…,wn),从而构成决策矩阵,本文将据此决策矩阵对备选方案进行排序和择优。

常见的属性类型有效益型和成本型。设I1和I2分别表示效益型和成本型的下标集,且令M=｛1, 2,…,m｝,N=｛1,2,…,n｝。为消除不同的物理量纲对决策结果的影响,可采用文献[3]的规范化方法处理,得到规范化矩阵其中且

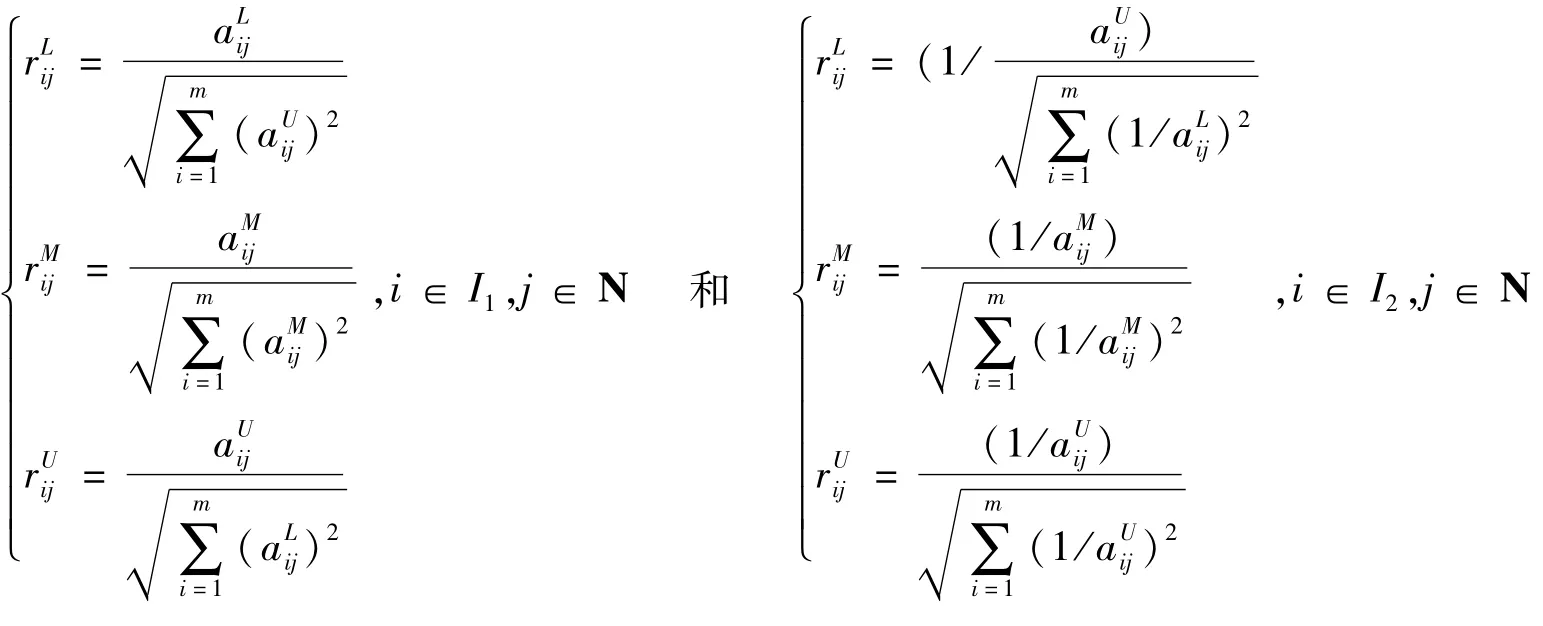
这里的属性值rij可以看成决策者在属性oi下对方案xj的客观偏好值。

在获得各方案的属性值后,由于属性值为三角模糊数无法直接排序,本文将基于文献[8]所提出的最大与最小集合法的思想,应用Fuzzy Max与Fuzzy Min与模糊数的交点定义左右得分值,进而将三角模糊数转化为区间数。左右得分值的定义如下:

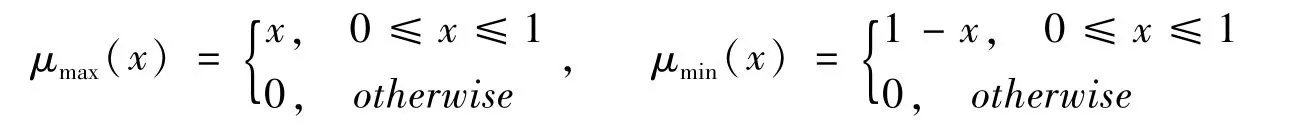
称LS和RS分别为三角模糊数=(rL,rM,rU)的左、右得分,若他们满足:

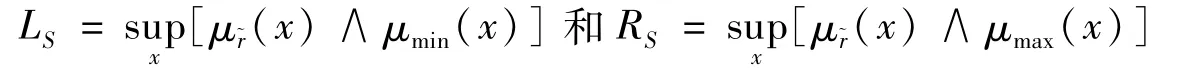
2 基于左右得分的多属性决策TOPSIS法

基于上面的讨论,我们给出基于左右得分的三角模糊数的多属性决策方法,具体步骤如下:

步骤3 定义正、负理想解:正理想解定义为:x+=([1,1],[1,1],[1,1],[1,1])负理想解定义为:x-=([0,0],[0,0],[0,0],[0,0])。

步骤4 利用均方差法[9]计算属性权重:

步骤5 计算备选方案xi与理想解x+及负理想解的距离x-:

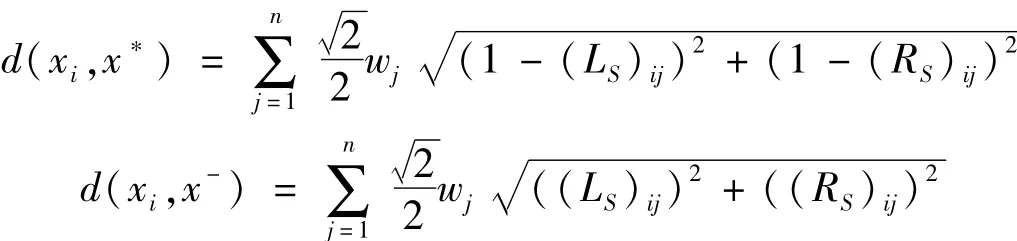
步骤6 计算各备选方案的相对贴近度:

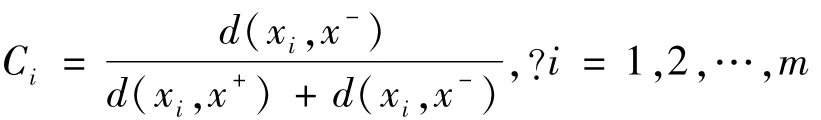
3 应用实例

下面以项目投资选择问题[11]为例说明本文所提出的方法的有效性和可行性.设经过初步筛选有5个备选企业xj(j=1,2,…,5)可作为投资企业,在评价时要考虑如下四个评价属性风险因素(o1)、成长因素(o2)、社会政治影响因素(ο3)和环境影响因素(o4),其中风险因素为成本型属性,其它均为效益型属性,各方案在各属性下的评价值均以三角模糊数的形式给出,具体属性值见表1,试对这五个备选企业进行排序以决定最佳投资企业。

表1 各备选企业在各项评价属性下的属性值

下面用本文的方法对五个备选企业进行排序,具体步骤如下:

步骤1 将表1中的模糊矩阵A=(aij)5×4转化为规范化的决策矩阵:

步骤2 计算得各方案相应的左右分值向量如下:

步骤3 确定正、负理想解:x+=([1,1],[1,1],[1,1],[1,1])和x-=([0,0],[0,0],[0,0],[0,0])。

步骤4 利用均方差法计算得属性权重为:w1=0.276 5,w2=0.288 9, w3=0.117 8,w4= 0.316 8。

步骤5 各备选方案xi与理想解x+及负理想解的距离x-分别为: d(x1,x*)=0.587 6,d(x2,x*)=0.539 1,d(x3,x*)=0.581 7,d(x4,x*)=0.536 1,d(x5,x*)=0.530 4 d(x1,x-)=0.413 4,d(x2,x-)=0.461 5,d(x3,x-)=0.418 9,d(x4,x-)=0.464 6,d(x5,x-)=0.470 1

步骤6 备选方案的相对贴近度为C1=0.413 0,C2=0.461 2,C3=0.418 7,C4=0.464 3,C5=0.469 9从而这五个备选企业的排序为x5＞x4＞x2＞x3＞x1,最佳备选企业为x5。

4 结语

本文针对项目投资选择问题提出了一种利用左右得分来表示决策者偏好的三角模糊数型多属性决策方法,避免了决策者过于乐观和过于悲观导致决策结果的主观不确定性。以左右得分区间来转化三角模糊数是一种区间折中的方法,是传统中庸思想向模糊数的拓展。本算法简单并易于用Matlab等软件进行程式化运算,为解决不确定多属性决策问题提供了新的思路。

[1] 徐泽水.对方案有偏好的三角模糊数型多属性决策方法研究[J].系统工程与电子技术,2002,24(8):9-12,20.

[2] 万树平.基于多维偏好信息的三角模糊数型多属性决策方法[J].统计与决策,2009(1):42-44.

[3] 潘丽娜.一种新的多属性决策方法[J].火力指挥与控制,2012,37(4):50-53.

[4] 陈晓红,阳熹.一种基于三角模糊数的多属性群决策方法[J].系统工程与电子技术,2008,30(2):278-282.

[5] 王美,张凤鸣,刘智.模糊信息的熵权多属性决策方案评估方法[J].系统工程与电子技术,2006,28(10):1523-1525.

[6] 林静,邱婉华.基于投影技术的三角模糊数型多属性决策方法研究[J].控制与决策,2009,24(4):637-640.

[7] 王修来,金洁,马宁玲,等.基于三角模糊数的我国博士后科研成果评价研究[J].科技进步与对策,2009,26(7):123-126.

[8] Chen SH.Ranking fuzzy numbers with maximizing set and minimizing set[J].Fuzzy Sets and Systems,1985,17:113-129.

[9] Rao R V,Patel B K.A subjective and objective integrated multiple attribute decision making method for material selection[J].Materials& Design,2010,31:4738-4747.

[10] Chen,C T.Extensions of the TOPSIS for group decision-making under fuzzy environment[J].Fuzzy Set Syst,2000,114:1-9.

[11] 卫贵武.基于模糊信息的多属性决策理论与方法[M].北京:中国经济出版社,2010.

TOPSIS of Left and Right Scores for Project Investment M ode l

LI Lan-ping
(Department of Basic Subjects,Hunan University of Finance and Economics,Changsha 410205,China)

Because of the limitation of knowledge and complexity of realistic decision,some property values of multi-attribute decision making often require fuzzy numbers.The triangular fuzzy number to describe this kind of ambiguity is very effective.As for the project investment selection problem with triangular fuzzy numbers,this paper proposes a new multi-attribute decision making method.The concrete steps are:we first define the left and right scores based on the normalized triangular fuzzy numbers,and then the decision matrix is transformed into the interval number decision-making matrix.Finally,the TOPSIS is used for sorting and merit of alternatives.At the end of the paper,the examples show that the method proposed is effective and practical.

multi-attribute decision making;triangular fuzzy number;left and right scores;TOPSIS

C943

A

1009-0312(2015)01-0077-04

2014-10-13

湖南省自然科学基金项目(2015JJ3030)。

李兰平(1981—),女,湖南永州人,副教授,硕士,主要从事模糊多属性决策研究。