电梯用永磁同步电机BP 神经网络PID 调速控制方法的研究

王同旭 马鸿雁, 聂沐晗

（北京建筑大学电气与信息工程学院 北京 100044）

1 引言

电梯是建筑中一种重要的垂直交通工具。在电梯中采用无齿轮曳引机具有节能、环保、运行平稳等优点，有着广阔的发展前景。永磁同步电机是转子励磁采用永久磁铁励磁的同步电机，有着体积小、结构简单、效率高、易于维护等优点[1]。因此它被广泛的应用于电梯无齿轮曳引机中。

PID 控制算法实现方便，应用范围广泛。PMSM是一种非线性的数学模型，应用于电梯曳引机时，其调速系统需要较好的控制精度和控制效果，PID控制难以满足其较高的控制要求[2]。为了提高电梯的控制效果，需要对传统的PID 算法进行改进。神经网络是一种智能控制方式,其特点是不依赖于定量模型，有较强的学习能力，比较适用于非线性度较高的控制对象[3]。BP 神经网络是一种发展较为成熟的神经网络，有着逼近任意非线性函数的能力，对于解决非线性的建模问题有着良好的效果[4]。

本文以电梯用 PMSM 调速控制系统为研究对象，在传统PID 算法的基础上加入BP 神经网络算法，通过建模和仿真，验证BP 神经网络PID 算法应用于电梯用PMSM 调速系统的有效性和可操作性。

2 永磁同步电机的数学模型

为了更好的对PMSM 的数学模型进行研究，需要做如下的设定[1]:

（1）三相绕组对称，产生的磁动势按正弦规律分布。

（2）不考虑磁路饱和以及铁芯损耗，忽略频率和温度变化等因素对绕组电阻造成的影响。

通过上述的设定，两相旋转d-q 轴坐标系下，永磁同步电机定子的电压方程如下:

磁链方程为:

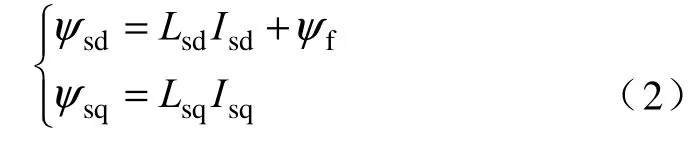
电磁转矩方程为:

式中 Usd、Usq——d、q 轴上的电压分量；

Isd、Isq——d、q 轴上的电流分量；

ωr——d，q 坐标系旋转角频率；

ψsd、ψsq——永磁体在d、q 轴上的磁链；

Lsd、Lsq——d，q 坐标系上的等效电枢电感；

ψf——永磁体产生的磁链；

Tem——电磁转矩。

3 永磁同步电机BP 神经网络调速系统

BP 神经网络学习算法属于局部逼近的方法，有着良好的逼近非线性映射的能力和较好的泛化能力[3]。将BP 神经网络算法与PID 控制相结合，采用BP 神经网络PID 参数自整定控制算法，可以改善PID 控制在非线性系统中的不足。采用BP 神经网络PID 参数自整定控制的结构图如图1 所示。

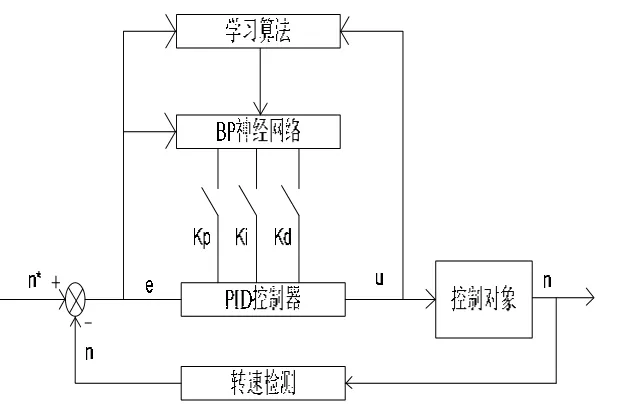
图1 BP 神经网络PID 参数自整定结构图Fig.1 The BP neural network PID parameters self-tuning structure

图1 中的神经网络控制器由传统PID 控制器和BP 神经网络两部分组成。其中PID 控制器对控制对象进行闭环控制，BP 神经网络对PID 的三个参数进行在线调节。PID 控制算法如（4）式所示。

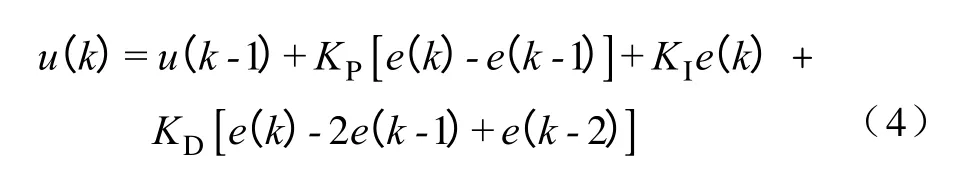
BP 神经网络算法分为正向传播和反向传播两部分。BP 神经网络的结构如图2 所示，第j 层是输入层，第i 层是隐含层，第l 层是输出层。

图2 BP 神经网络结构Fig.2 The structure of BP neural network

3.1 BP 神经网络算法

第j 层的输入量:

第i 层的输入量:

第i 层的输出量:

第l 层的输入量:

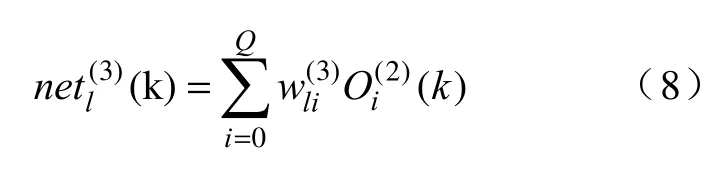
第l 层的输出量:

第l 层神经元激活函数为:

性能指标函数:

为了使收敛速度加快，附加一个惯性量。得到根据梯度下降法修正神经网络的权系数的公式如（15）所示。

通过式（4）和式（15）可以得到下式:

通过以上各式可以得到第l 层的权值学习算法和第i 层的权值学习算法，分别如式（19）和式（20）所示:

式中:η为学习率；

α为动量项因子；

3.2 BP 神经网络PID 控制算法流程

（1）建立BP 神经网络:确定网络的层数和每层的节点数，选取初始权值wij，学习率和动量项因子。

（2）计算k 时刻的误差e(k),

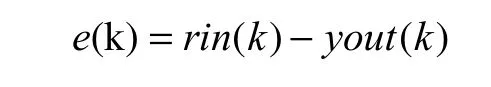
（3）计算网络各层的输入、输出。

（4）计算PID 控制器的输出。

（5）进行反向传播计算，对输出层权值、隐含层的权值进行修正。

（6）设k=k+1，返回步骤（2）。

4 永磁同步电机调速系统仿真研究

4.1 仿真模型

永磁同步电机BP 神经网络PID 参数自整定调速系统如图3 所示。系统采用双闭环控制，电流环是内环，采用PI 控制，转速环是外环，采用BP 神经网络PID 控制。逆变方式为电压空间矢量PWM。

图3 永磁同步电机BP 神经网络PID 参数自整定调速系统Fig.3 The parameters self-tuning control system of PMSM BP neural network PID control

仿真中所用的PMSM 的具体参数如下所示[5]:极对数 p=1，定子电阻 Rs=2.875 Ω，磁链ψf=0.175Wb，定子d 轴电感Ld=0.0085H，定子q 轴电感 Lq=0.0085H，转动惯量J=0.0008kg⋅m2。

4.2 仿真结果分析

设给定转速为1500r/min，仿真时间为0.2s，在0.1s 时，突加T=3N 的负载，神经网络的结构是3-6-3，学习率η=0.25，动量项因子α=0.05。将采用PI 控制和BP 神经网络PID 控制的永磁同步电机调速系统进行仿真比较。BP 神经网络PID 控制的电机转速如图4 所示，PI 控制的电机转速如图5所示。

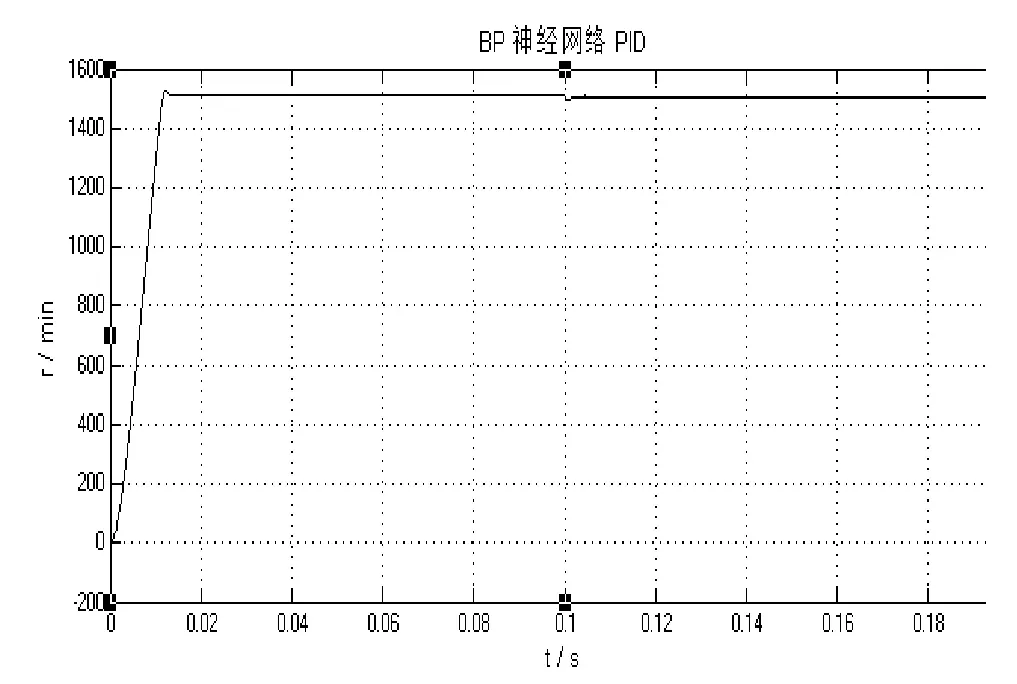
图4 BP 神经网络PID 控制的电机转速Fig.4 The motor speed BP neural network PID control

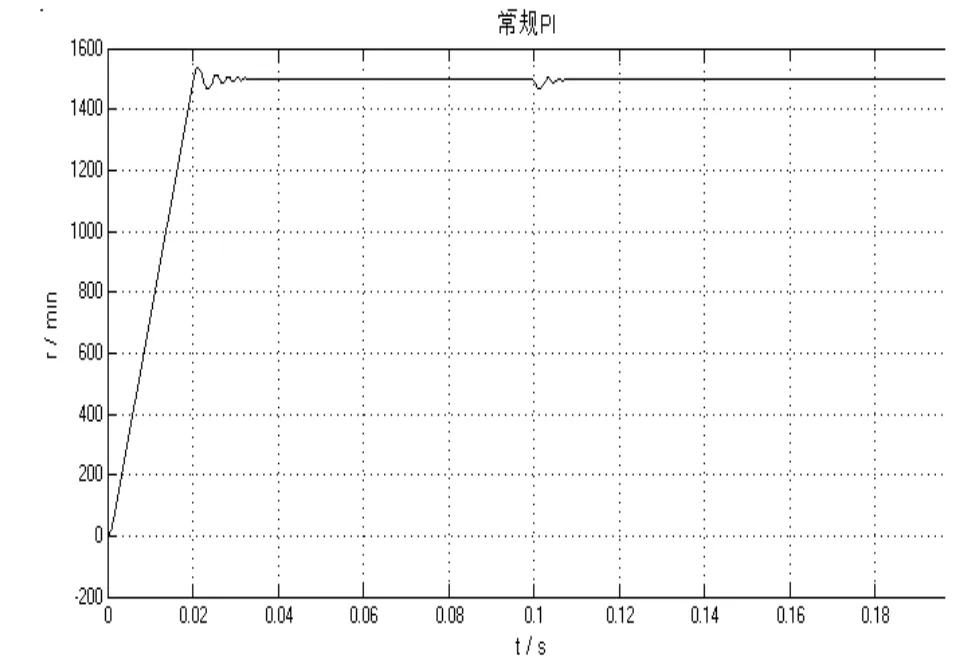
图5 PI 控制的电机转速Fig.5 The motor speed of PI control

在0.1s 突加负载时，两种控制方式下的电机转速变化情况如图6、图7 所示。

图6 PI 控制的电机转速降Fig.6 The motor speed drop of PI control

从图6～7 可以看到BP 神经网络PID 参数自整定算法有着较好的动态性能。在突加负载时，PI 控制的电机转速下降为50r/min，而BP 神经网络PID控制的电机转速下降为12r/min。两算法的电机转速动态性能比较如表1 所示。

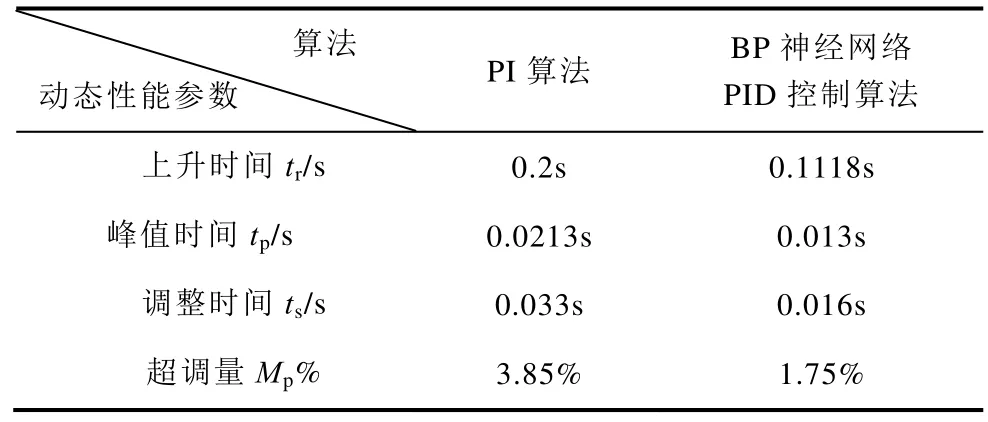
表1 电机转速动态性能比较表Tab.1 The dynamic performance comparison of motor speed

从表1 可以看出，采用BP 神经网络PID 控制算法后，电机的上升时间从0.2s 减小的0.1118s，调整时间从0.033s 减小到0.016s，超调量从3.85%降低到了1.75%。

在电机刚开始转动的过程中，PI 控制算法控制的电机振动较大且耗时较长。BP 神经网络PID 算法控制的电机在启动阶段振动比较小且耗时很短，能迅速的稳定下来。在突加负载阶段，PI 控制方式下的电机转速下降的较多，恢复稳定转速所需时间较长。而BP 神经网络PID 控制下的电机转速下降很小，且能快速的恢复稳定，具有较好的鲁棒性。

综上所述，BP 神经网络PID 控制算法的控制性能明显优于PI 控制算法，具有响应速度快、自适应能力强和较好的鲁棒性等优点。在PMSM 调速控制系统中采用BP 神经网络PID 控制算法，可以提高其控制性能。

5 系综合考虑电梯舒适性和快速性的仿真研究

快速性与舒适性是交通工具应该具备的重要特征。根据相关规范规定，要求电梯的启动和制动应平稳、迅速，加减速度最大值不大于1.5m/s²。加加速度不超过1.3m/s³。[6]

常用的电梯速度曲线一般为抛物线形。为了研究BP 神经网络PID 控制算法下电梯速度曲线的控制效果，现根据电机转速1500r/min 设计相应的电梯速度曲线如式（21）所示，其中0～3s为电梯启动阶段的速度曲线，3～6s为电梯匀速运行阶段6～9s为减速阶段的速度曲线。

从图8 中可以看出，设计的电梯速度曲线符合电梯的运行特点。

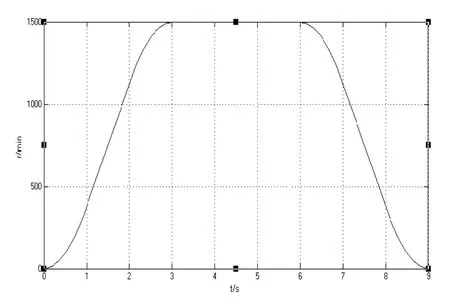
图8 电梯速度给定曲线Fig.8 The given curve of elevator speed

将上述电梯速度曲线作为电机调速系统的给定速度，进行仿真，得到BP 神经网络PID 参数自整定控制算法下的电梯速度曲线，如图9 所示。

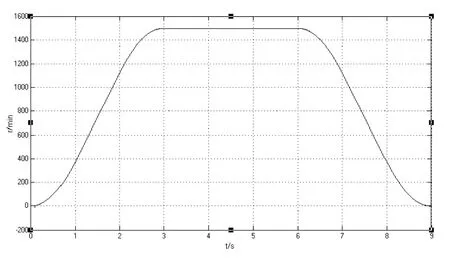
图9 电梯实际运行速度曲线Fig.9 The actual speed curve of the elevator

对比图8、图9 可以得到:BP 神经网络参数自整定控制算法下的电机速度曲线与设计的电梯速度曲线相一致。说明此算法控制下的电梯用PMSM可以较好的跟随给定速度信号运行。

6 结论

本文建立了永磁同步电机BP 神经网络PID 调速控制系统的仿真模型，并进行了仿真。通过与PI控制的PMSM 调速系统的对比表明:BP 神经网络PID 控制算法用于PMSM 调速系统时，可以明显的提高系统的响应速度，同时减小振荡幅度，具有较好的鲁棒性，在动态性能上有较为明显的提高。

通过结合电梯速度曲线的仿真研究验证了 BP神经网络PID 控制算法用于电梯曳引机控制算法的可行性。BP 神经网络 PID 控制算法用于电梯用PMSM 时，可以满足电梯高精度的控制要求。

[1]陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2009.

[2]李广军,张晶,曾安平.基于BP 神经网络的PID 控制器研究[J].计算机仿真,2009-9.Li Guang-jun,Zhang Jing,Zeng An-ping,PID Control Based on BP Neural Network[J].Computer simulation,2009-9

[3]孙增圻.智能控制理论与技术[M].北京:清华大学出版社,2011.

[4]刘星洋、王子剑、张宝利.基于BP 神经网络的永磁同步电机的转速控制[J].电工研究,2013.1(2):41-42.Liu Xing-yang,Wang Zi-jian,Zhang Bao-li,Speed control of PMSM based on BP neural network[J].Electrician research,2013.1(2):41-42.

[5]洪乃刚.电力电子、电机控制系统的建模和仿真[M].北京:机械工业出版社,2010.

[6]叶安丽.电梯控制技术（第2 版）[M].北京:机械工业出版社,2008.