基于LDA 模型的稀疏消息传递算法

屠雄刚 陈 军 杨 璐 严建峰

（1.浙江工业职业技术学院设计与艺术学院 绍兴 312000 2.苏州大学计算机科学与技术学院 苏州 215006 3.苏州大学江苏省计算机信息处理技术重点实验室 苏州 215006）

1 引言

潜在狄利克雷分配（Latent Dirichlet Allocation,LDA）[1]是识别大规模文本集或语料库中潜在主题信息的概率主题模型，它能够将单词空间中的文档变换到主题空间，得到文档在低维空间中的表达。LDA 假定每篇文档是主题的一个概率组合，而主题是单词表中单词的多项分布。文档-主题分布可以看作是文档在主题空间的表示，能够被用来分类以及检索，而主题在单词的分布能被用来表示主题的意义。然而这样的LDA 模型不能直接控制推理参数的后验稀疏度。

在文本模型中语义空间的稀疏表示具有实际的应用价值，通常每篇文档或每个单词只有几个突出的主题意义，而不是在每个主题上都有非0 的值。单词的主题分布越稀疏就能越清晰的反映出单词的主题意义，在模型参数估计和推理的过程中增加稀疏限定可以提高模型的精度。稀疏主题编码（Sparse Topical Coding，STC）[2]是发现大规模文本集隐藏表示的非概率主题模型，与概率主题模型不同，STC松弛了混合比例和最大似然函数的标准化限定，使用稀疏规则化的方法直接控制推断表示的稀疏性，无缝地结合凸误差函数到监督学习中，有效地学习半监督结构化的条件下降算法。稀疏编码的潜在狄利克雷分配（SCLDA）[3]是一个加入稀疏限定的基于连续特征的主题模型，假定连续单词的概率分布是拉普拉斯分布，该分布的参数依赖于主题，使用期望最大化（Expectation Maximization,EM）算法估计模型参数，该模型在计算机视觉问题中取得了不错的效果。稀疏隐藏语义分析（Sparse Latent Semantic Analysis,SLSA）[4]在L1范数约束的条件下产生了一个稀疏投影矩阵。与传统的LSA 相比，SLSA 紧紧选择每个主题的少数几个单词，提高了主题-单词分布的可解释性，在内存和效率上也有相应改进。变分贝叶斯（Variational Bayes，VB）[1]、塌陷吉布斯采样法（Collapsed Gibbs Sampling，GS）[5]以及消息传递算法（Belief Propagation，BP）[6]是LDA 的三种近似推理算法。BP 算法把计算全局积分的过程分散到各个节点的信息传递，而各个节点和邻近节点交互信息，它在效率和准确率上都明显优于VB 和GS 算法。本文的研究是在消息传递算法的基础上进行的。

LDA 模型的先验参数可以在一定程度上控制文档-主题分布和主题-单词分布的稀疏度，然而因概率主题模型的标准化操作而很难获得稀疏的主题表示。稀疏非负矩阵分解[7]提供了一个在原来算法基础上获得向量稀疏表示的基本框架。本文在前人研究的基础上，提出了稀疏限定的消息传递算法（sparseBP），用基于L1范数和L2范数的方法度量向量的稀疏度，在算法的迭代过程中投影单词在主题上的概率分布到稀疏空间，从而得到特定稀疏度的单词在主题上的分布。本文也探索了sparseBP 的聚类性能，并把sparseBP 看作是一种降维算法，把文档在主题上的分布作为libsvm 分类器的输入探索文本分类准确率。

2 消息传递算法

消息传递（Belief propagation,BP）最初被机器学习专家用于树状结构的统计推断，后来这种算法忽略掉它本来对树状结构的要求而应用与带环的模型。文献[1]在马尔科夫随机场的框架下证明了在主题模型意义下LDA 是一种特殊的因子图，并提出用消息传递算法近似求解LDA 模型。本文中用到的符号见表1。

表1 符号标签Tab.1 Symbol labels

图1 基于因子图的消息传递Fig.1 Message passing based on factor graph

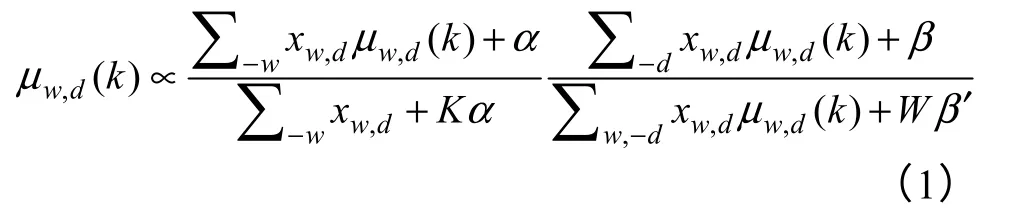
这里 -w 表示除了单词w 以外的所有单词，-d表示除了文档d 以外的所有文档。信息更新式（1）取决于除了当前信息μw,d以外的所有其他邻接信息μ-(w,d)。文档-主题分布θ 和主题-单词分布φ 的计算公式为

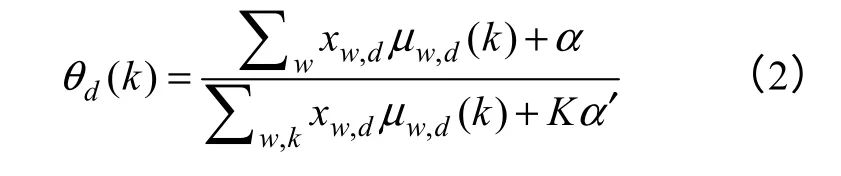
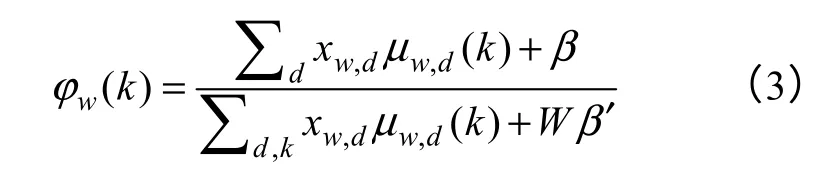
信息更新过程将通过迭代公式（1），直到信息收敛于一个固定的点。算法的执行过程如图2 所示，算法的迭代过程分为两个步骤，第一步更新每个单词的主题分布μw,d,第二步用更新的消息μw,d估计参数dθ 和wφ 。

图2 消息传递算法Fig.2 Message passing algorithm

3 稀疏消息传递算法

本节首先描述稀疏度的概念，然后介绍如何把稀疏度结合进LDA 模型的消息传递中，最后介绍算法具体执行过程。

3.1 稀疏度

向量稀疏度的度量可以用向量中0 元素的数目与向量维度的比值来计算。对于大部分元素取值接近与0 而只有几个有意义的非0 值的向量会有一个较低的稀疏度，然而在实际应用中，这样的向量被认为有一个较高的稀疏度。本文使用基于L1_norm和L2_norm的稀疏度度量方式[7]

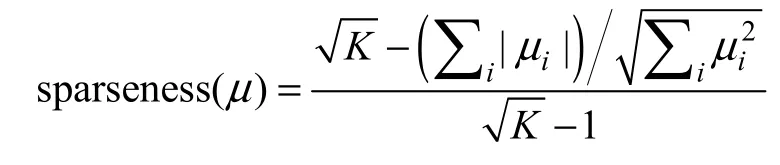
其中K 表示μ 的维度，当向量μ 只有一个非0的元素时稀疏度为1，当向量μ 的所有元素都相等时稀疏度为0。

3.2 稀疏限定的消息传递

消息传递算法可以看作是对语料库中的单词分配标签的过程，通常每个单词的主题集合只有小部分是活跃的。在消息传递算法的迭代过程中对于单词-文档矩阵中的非0 元素都需要通过公式1 来得到单词的主题分布，这个分布往往是很稀疏的。稀疏度随着迭代次数的增加而不断增加。像“learning，paper，algorithm”这样的常用词往往有一个较低的稀疏度，而像“network neural genetic”这样的关键词有较高的稀疏度。主题模型中主题数目K 通常是启发性的设置或者是通过非参数的贝叶斯模型学习得到，当K 初始设置的数目比较大时，常用词和关键词的主题分布的稀疏度可能有更大的差距。本文中我们固定主题在单词分布上的稀疏度，每次迭代得到μw,d后把它投影到与它距离最近的稀疏空间中去，而向量的稀疏度可以自由设定，通常越稀疏的向量越能清晰的反应单词的主题分布。然后整合出LDA 模型的两个输出文档-主题分布和主题-单词分布。这种增加稀疏度限定的消息传递算法称为稀疏消息传递算法（sparseBP），算法的具体执行过程如图3 所示。

图3 稀疏消息传递算法Fig.3 Sparse message transfer algorithm

投影向量到稀疏度为S 的空间的具体操作如算法3 所示，该算法首先投影给定的向量到L1的空间中，然后投影到与之最接近的由L1和L2联合限定的空间中。如果投影结果完全是非负的，就退出循环，而如果有负值，把负值设置为0，然后在额外限定的条件下去寻找一个新的点。原则上，算法的迭代次数和向量的维度是相等的，因为算法的一次迭代过程或者是收敛，或者是增加一个值为0 的元素。而事实上，算法可以收敛的更快。

3.3 复杂度分析

消息传递算法需要存储单词的主题概率分布，在存储和计算方面都要乘以主题数目K 的倍数，消息传递算法的时间复杂度 O (KDWdT)，sparseBP 在BP 算法的基础上增加了投影操作，sparseBP 的时间复杂度为 O (K2DWdT)。sparseBP 在投影的过程中增加了几个维度为K 的向量，然而它的空间复杂度与消息传递算法相同，均为 O (K * NNZ)，其中D 是输入文档-单词共现矩阵的列数，Wd是共现矩阵每一列中非零单元 xw,d≠ 0的个数，T 是算法的迭代次数，NNZ 为单词-文档共现矩阵中非0 元素的总数目。

图4 投影向量到稀疏度为s 的空间的算法Fig.4 projection vector to the sparse degree s of space algorithm

4 实验分析

本文的实验在Matlab C/C++MEX 平台上进行，这个平台在文献[8]中已经被使用。先验参数初始化设置为 α=2/K， β=0.01，这里K 是主题的数目，对于所有的算法分别做300 次迭代并运行5 次计算其均值。每篇文档中单词的概率分布μw,d的稀疏度S 在0.7～0.9 之间变化时，效果基本一致，这里固定S 为0.8。本文采用标准化互信息来评估文档聚类的准确率，并使用常用的聚类方法BP，GS，非负矩阵分解（Non-negative Matrix Factorization,NMF）[9]，谱聚类（Spectral Clustering,SC）[10]来进行对比。此外，使用消息传递算法对文档-单词共现矩阵进行降维，并借助于libsvm 测量文本的分类准确率，使用BP，GS 和NMF 来和sparseBP 进行对比。在评价sparseBP 在文档聚类和分类中相比其它算法提高的百分比时本文采用的计算公式为：

4.1 数据集选择

本文在英文语料上进行测试，采用CORA[11]和TEUTERS[12]两个通用的文本数据集进行实验。实验所用文本数据如表1 所示，这里D 是文档的总数目，W 是单词表的大小，N 是文档中单词的总数目，Ave( d) 是文档的平均长度，classes 是文档集中文档的类别数目。文档去除了停用词以及单词的后缀，采用1-Gram 的表示法，使用单词在文档中出现的次数作为文档的特征。

表2 数据集Tab.2 Data sets

4.2 文档聚类分析

稀疏消息传递算法可以用来做文本聚类，算法得到文档在主题的分布 θd(k)是文档在主题上的概率分布，在模型的训练过程中不使用数据真实的类别标签，得到 θd(k)后选出每篇文档最可能的主题，并使用标准化互信息评估算法的聚类准确率。

4.2.1 聚类评价标准

标准化互信息（Normalized Mutual Information,NMI）[13]是一种被广泛应用的外部聚类评价标准，通过比较数据集的聚类结果和该数据集的真实划分的相似程度来实现，而在聚类过程中不使用文档的类别标签。NMI 可以在预测类别和真实类别不同时利用互信息进行评测，NMI 的计算公式为：

式中，hn 是类别为h 的文档的总数目，ln 是类别为l的文档的总数目，nh,l是同时为类别h 和l 的文档的总数目，n 是数据集中文档的总数目，h 是真实的类别标签，l 是用聚类算法得到的预测类别标签。NMI 是介于0～1之间的值，当聚类标签和外部真实标签完全一致时NMI 值为1，而当随机划分时NMI值为0，NMI 值越大表示有越好的聚类准确率。

4.2.2 聚类实验结果

图5 和图6 分别表示了当主题数目K={50,75,100,125,150}时5 种算法在CORA 和TEUTERS 数据集上的NMI。从图中可以看出，在两个数据集上sparseBP 的NMI 都是最好的，胜过了其它的文本聚类方法，例如，在CORA 数据集上，当主题数目为100 时，sparseBP 胜过其它四种方法分别为3.67%，9.68%，32.21%和60.18%。结果表明稀疏消息传递算法提高了文档聚类的准确率。

图5 CORA 数据集上的NMI 比较Fig.5 NMI comparison on CORA data sets

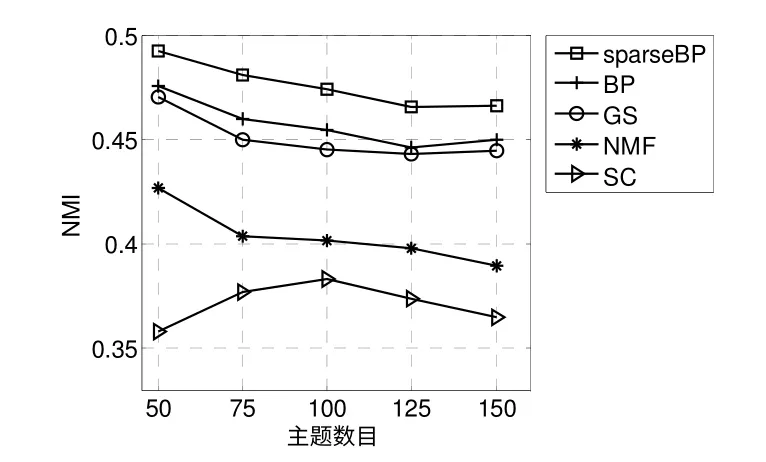
图6 TEUTERS 数据集上的NMI 比较Fig.6 NMI comparison on TEUTERS data sets

4.3 文档分类分析

首先使用sparseBP 把语料库中的文档-单词矩阵投影到隐藏主题空间当中得到文挡-主题分布，然后以4：1 的比例随机划分低维的文档特征数据为训练集和测试集，最后根据已知文档的类别标签使用libsvm 分类器去分类文档。在使用libsvm 分类时，采用网格搜索法学习参数C 和G。

4.3.1 分类评价标准

准确率（Accuracy）是评价文本分类结果优劣的一种常用评价标准，其计算公式为：

Accuracy 是介于0%～100%之间的值，越高的类别准确率暗示基于主题的低维特征具有越好的区分能力，即在降维的过程中提取到了高质量的文档特征。

4.3.2 分类实验结果

图7 和图8 分别显示了当主题数目K={50,75,100,125,150}时5 种算法在CORA 和TEUTERS 数据集上的Accuracy。从图中可以看出sparseBP 总是有最好的分类准确率，例如，在CORA 数据集上，当主题数目为100 时，sparseBP 胜过BP，GS 和NMF分别为3.81%，8.21%和14.03%。在RETURE 数据集上，当主题数目为100 时，sparseBP 胜过BP，GS 和NMF 分别为1.83%，1.73%和0.18%。谱聚类不能获得文档-主题这样的分布，于是这里没有相关对比结果。

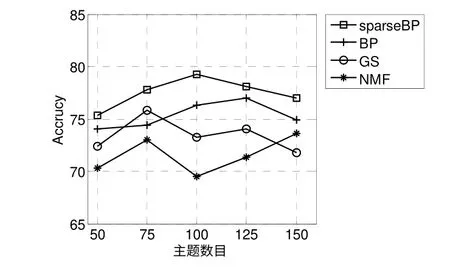
图7 CORA 数据集上的Accuracy 比较Fig.7 Accuracy comparison on CORA data sets

图8 TEUTERS 数据集上的Accuracy 比较Fig.8 Accuracy comparison on TEUTERS data sets

5 结束语

本文提出了把稀疏限定加入到消息传递算法中，在迭代的过程中将向量投影到稀疏空间中去，同时也探索该方法对文本聚类以及分类准确率的影响。丰富的实验结果表明本文提出的加入基于 L1范数和L2 范数的稀疏消息传递算法提高了文本的聚类以及分类准确率。进一步的研究工作将主要围算法在其它方面的应用以及时间效率的因素开展，以便使算法适应于更多的应用并提高算法的执行效率。

[1]David M.Blei,Andrew Ng and Michael Jordan,Latent Dirichlet Allocation[C].Neural Information Processing Systems,2001:601-608.

[2]Jun Zhu and Eric P.Xing.Sparse Topical Coding[C].Uncertainty in Artificial Intelligence,2011:267-286.

[3]Wenjun Zhu,Liqing Zhang and Qianwei Bian.A hierarchical latent topic model based on sparse coding[J].Neuro Computing,2012,76(1):28-35.

[4]Xi Chen,Yanjun Qi,Bing Bai,Qihang Lin and Jaime G.Carbonell.Sparse latent semantic analysis[C].SIAM International Conference on Data Mining,2011:474-485.

[5]Gregor Heinrich.Parameter Estimation for Text Analysis[R]. Fraunhofer IGD,2004.

[6]Jia Zeng,William K.Cheung,Jiming Liu,Learning topic models by belief Propagation[J],IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,33(5):1121-1134.

[7]Patrik O.Hoyer.Non-negative Matrix Factorization with Sparseness Constraints[J].Journal of Machine Learning Research,2004,5(1):1457-1469.

[8]Jia Zeng.A topic modeling toolbox using belief propagation[J],Journal of Machine Learning Research,2012,13(1) 2233-2236.

[9]Daniel D.Lee and H.Sebastian Seung.Algorithms for non-negative matrix factorization[C],Neural Information Processing Systems,2002:556-562.

[10]Ulrike Luxburg.A Tutorial on Spectral Clustering[J].Journal Statistics and Computing,2007,17(4):395-416.

[11]Andrew McCallum,Kamal Nigam,Jason Rennie and Kristie Seymore.Automating the construction of internet portals with machine learning[J].Information Retrieval,2000,3(2):127-163.

[12]Deng Cai,Xiaofei He,Jiawei Han.Document clustering using locality preserving indexing[J].IEEE Transactions on Knowledge and Data Engineering,2005,17(12):1624-1637

[13]Shi Zhong and Joydeep Ghosh.Generative modelbased document clustering:a comparative study[J].Knowledge and Information Systems,2005,8(3):374-384.