基于分布式天线的全双工中继系统最大化和速率波束成形设计

徐霄飞 陈 翔 赵 明 周世东 王 京



基于分布式天线的全双工中继系统最大化和速率波束成形设计

徐霄飞①②陈 翔*③赵 明②周世东①王 京②

①(清华大学电子工程系 北京 100084)②(清华大学信息科学与技术国家实验室 北京 100084)③(中山大学信息科学与技术学院 广州 510275)

基于分布式天线的全双工中继系统结合了全双工中继两跳同时同频传输的能力和分布式天线高效覆盖的特性，为提升小区边缘和严重阴影衰落区域的频谱效率提供了一种有效途径。在自干扰抵消非理想的多用户场景下，利用分布式多天线波束成形可实现对系统中自干扰和多用户干扰的联合抑制。为此，该文首先建立了在各分布式天线节点独立发射功率约束下最大化多用户端到端和速率的最优化系统模型，进而提出一种双层迭代算法，解决原问题的非凸性求解难题。仿真结果验证了算法的有效性，表明在多用户分布式天线全双工中继系统中，所提波束成形设计能够有效抑制自干扰和多用户干扰，显著提高系统频谱效率。

全双工中继；分布式天线；波束成形；干扰抑制；和速率

1 引言

蜂窝移动通信系统中，复杂的无线传播环境严重制约了系统频谱效率的提升。在小区边缘和阴影衰落严重的区域，由于基站到用户直连链路上严重的路径损耗，频谱效率十分低下，远远不能满足用户对于无缝高速接入的需求。中继[1]技术的提出为这一问题提供了一种有效的解决方案。利用基站与中继之间和中继与用户之间的较低损耗链路，中继能够利用两跳传输为远端用户提供更好的服务，在有限的发射功率下实现更高的频谱效率，从而提升通信系统的有效性。然而，已有研究中的中继大多工作在半双工模式[2,3]，两跳传输在不同的时隙或频带中进行，以避免同时同频收发带来的严重自干扰，使得频谱效率的提升相对有限。

近年来，随着自干扰抵消技术[4]的发展，全双工中继的实现成为可能。利用模拟域、数字域和空域多种自干扰抵消技术的结合，全双工中继能够在有限的残余自干扰下，实现两跳链路同时同频收发[5,6]，弥补了半双工中继在频谱效率上的不足，拓宽了中继技术的应用场景。由于这一优势，全双工中继在3GPP LTE-A, IEEE 802.16等新一代无线通信标准的研究中受到广泛关注。

在全双工中继的相关研究中，多天线全双工中继由于其在空域自干扰抑制上的潜力而被广泛研究。然而，在基站半径较大或传播环境复杂时，集中式天线中继提供的覆盖不足以满足实际需求。为解决这一问题，文献[10]提出了分布式天线全双工中继的架构，利用集中式处理和分布式天线为大面积复杂环境中的用户提供有效覆盖[11]。此外，利用收发天线分离，这一架构能够缓解自干扰，降低硬件复杂度。然而，对此架构的研究仍有不足。首先，文献[10]假设自干扰可被彻底消除，但已有原型系统表明，由于硬件非理想，残余自干扰不可忽略，并对系统性能有明显影响[12]。第二，上述研究，包括集中式天线中继的相关研究，往往局限于单用户场景，而在蜂窝移动通信系统中典型的多用户场景下，如何同时抑制自干扰和多用户干扰，从而充分发挥分布式天线全双工中继系统的性能潜力，尚无有效的方案。

为此，本文在多用户分布式天线全双工中继系统中，提出一种基于波束成形的传输方案，对信道进行自适应，实现自干扰和多用户干扰的联合抑制。结合中继资源分配问题中max-min函数的等价形式和连续凸近似(successive convex approximation)[13]，设计了一种高效的双层迭代算法，在基站和中继各节点独立发射功率约束下，最大化多用户端到端和速率，从而最大限度提升分布式天线全双工中继系统的频谱效率。

本文余下内容结构如下。在第2节对系统模型进行描述，并构造了相应的优化问题；第3节设计了一种迭代算法，对优化问题进行高效求解；在第4节利用仿真对算法的有效性进行验证，并对仿真结果进行分析；最后在第 5 节中给出本文的结论。

2 系统模型与问题构造

一个多用户分布式天线全双工中继系统的模型如图1所示。考虑下行传输，基站利用中继同时为个用户提供服务。基站天线数为,个用户均为单天线。中继的接收天线数和发射天线数分别为和，这些天线分布式部署在待覆盖区域内，通过高速本地连接(如光纤等)与集中式处理单元相连，各天线收发的基带信号可在集中式处理单元中进行联合处理。中继工作在译码转发的全双工模式下，在基站-中继链路和中继-用户链路上同时同频传输，因此中继的接收天线会受到发射天线的自干扰。由于基站与用户间直连链路上的严重损耗，系统中直连链路的影响可忽略。

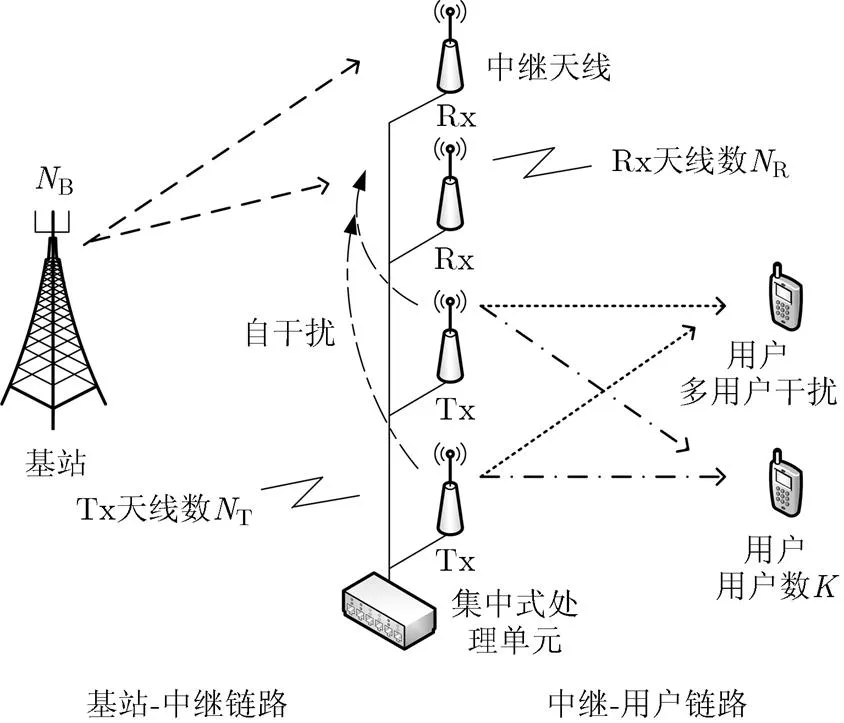
图1 多用户分布式天线全双工中继系统模型

利用周期性的信道估计及信道互易性，本文假设中继能够获得各链路上准确的信道增益，且每次端到端传输时长远小于信道衰落相干时间(即保持准静态)。当用户静止或低速移动时，这一假设是合理的。将基站-中继链路、中继-用户链路和自干扰链路上的信道增益分别用,和表示，则在中继-用户链路上，第个用户接收信号可表示为

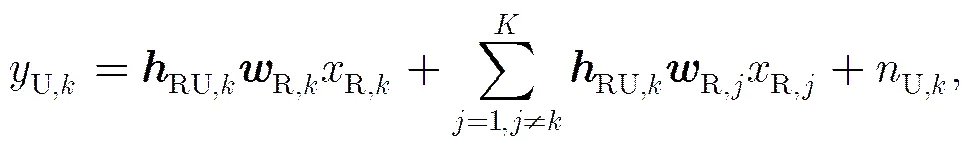
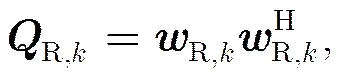
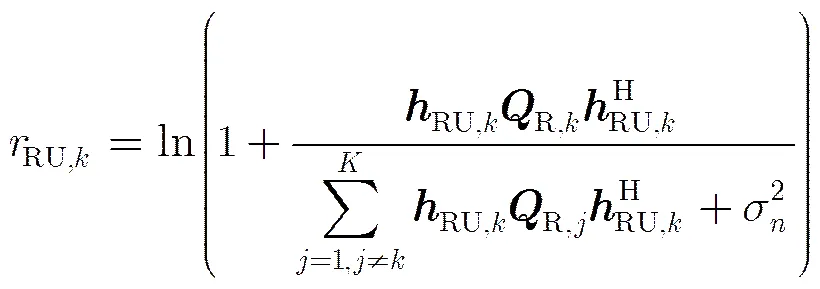
在基站-中继链路上，为充分利用中继的多接收天线，采用多流传输。用和分别表示基站的发送符号向量和波束成形矩阵，则中继接收的信号可表示为

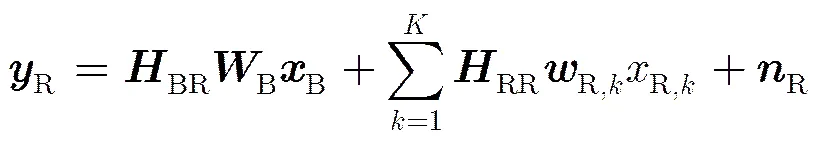
接下来集中处理单元使用最小均方误差-串行干扰抵消(Minimum Mean Square Error Successive Interference Cancellation, MMSE-SIC)接收机对接收信号进行检测，定义基站处的发送相关矩阵为

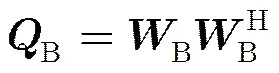
则基站-中继链路上的信息速率可表示为

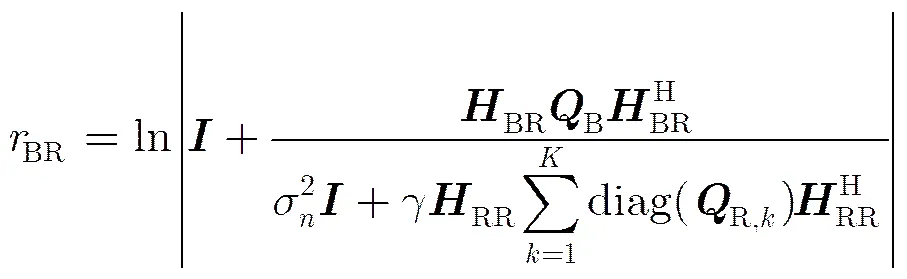
由式(3)和式(7)可知，在多用户分布式天线全双工中继系统中，自干扰和多用户干扰共同制约了系统性能的提升。通过对中继波束成形矢量和基站波束成形矩阵的优化设计，可以实现对多用户干扰和自干扰的联合抑制，从而提高端到端传输速率。

在多用户系统中，和速率是反映系统频谱效率最直观的指标，为此本文选择系统端到端和速率作为优化目标。由于全双工中继的连续传输要求两跳链路速率平衡，系统端到端和速率等于基站-中继链路速率与中继-用户链路速率两者的较小值。考虑中继处多个分布式天线具有独立功率约束，基站集中式天线具有和功率约束。利用半正定松弛[14]，忽略矩阵和的秩约束，则优化问题可表示为

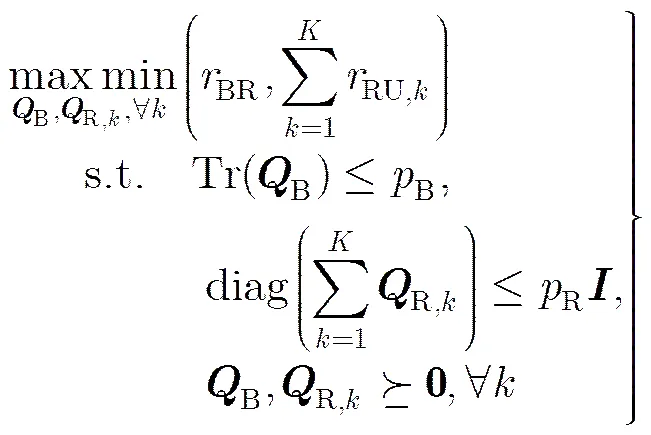
分析可知，式(8)是一个目标函数不可导且非凸的优化问题，其全局最优解的计算需要复杂的全局优化理论，相应算法复杂度是非多项式的，难以实际应用。因此有必要设计一种低复杂度的可行算法，对式(8)进行高效求解。

3 算法设计

本节给出一种迭代算法，利用中继资源分配问题中max-min函数的等价形式和连续凸近似对问题式(8)进行高效求解。

首先，将问题式(8)中max-min形式的目标函数转化为可导的加权和速率形式[15]。定义和。问题式(8)的约束定义了在全空间上的一个可行集，用表示；而问题式(8)的最优解又构成了的一个子集，用表示。利用以上定义，易知，通过对或乘以一个小于1的正系数，总可获得一个最优解，使得两跳链路速率相等，即。定义集合，包含集合中所有使得两跳链路速率相等的(不一定满足)，则问题式(8)等价于

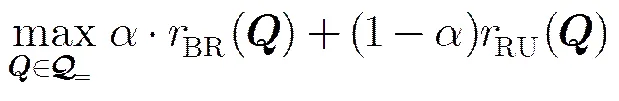
至此原问题式(8)被转化为一系列具有连续可导目标函数的优化问题式(10)，对应不同的取值。接下来，在给定取值时，本文利用连续凸近似将问题式(10)近似为一系列迭代的凸问题，以便利用通用的凸优化工具(如拉格朗日对偶法、内点法(interior point method)[16]等)高效求解。

问题式(10)的非凸性来自于式(7)和式(3)里分母中的项。利用对数行列式函数的凹性，易知对任意，有式(11)不等式：

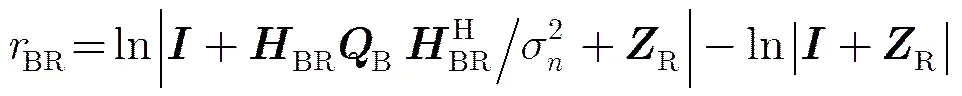
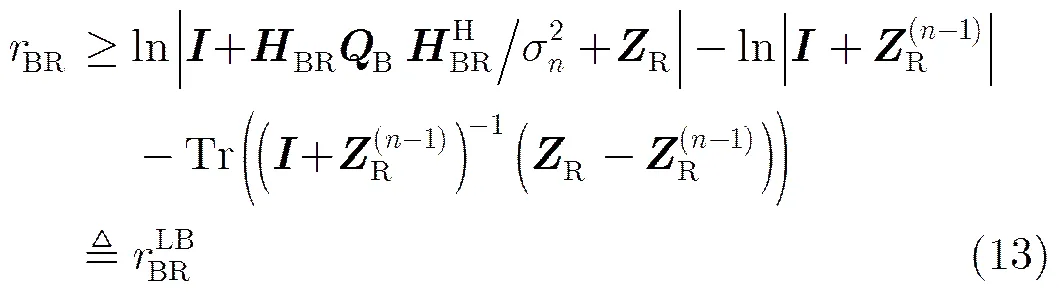
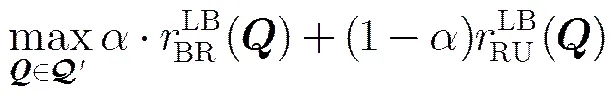
该问题的目标函数给出了问题式(10)的一个下界。求解问题式(14)，完成此次迭代。

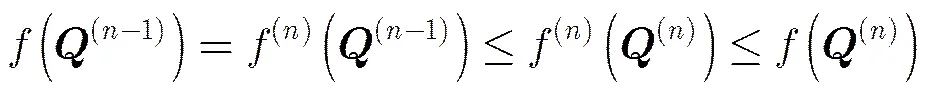
其中左侧等式和右侧不等式由式(11)可证，中间不等式由问题式(14)的凸性可证。因此问题式(10)的目标函数将随着迭代进行不断增大直至收敛。当迭代的初始值和满足特定条件时(参见文献[13])，问题式(14)的目标函数可收敛为问题式(10)的全局最优解；而对于任意选择的初始值，以上算法也可保证问题式(14)的目标函数收敛为问题式(10)的局部最优解。对于凸优化问题式(14)，可以利用通用的凸优化工具高效求解，在此不再赘述。

至此给出了一种双层迭代算法，能够对问题式(8)进行高效求解。将其总结为算法1，步骤如下：

关于算法1 的复杂度，可由外而内逐层进行分析。首先，对于外层迭代，定义，存在以下定理：

对于内层迭代所需次数，由于一般条件下连续凸近似仅可保证局部最优解，相应的收敛速率难以分析，在已有文献中也缺乏相关研究，一般借助仿真或经验给出最大迭代次数[13]。通常而言，连续凸近似的收敛速率与目标函数的形式有关，对于较为简单的函数形式(如式(10)中的目标函数，较小时)，一般在10次迭代之后，继续迭代的性能增益即可忽略。

在步骤3中，每一次内层迭代需要对问题式(14)进行求解。该问题是一个凸的非线性半定优化(Non-Linear Semi-Definite Programming, NLSDP)问题。对于一般的NLSDP问题，文献[17]给出了一种复杂度为的算法，其中和分别表示优化变量中标量元素的个数和约束集的维度。在问题式(14)中，中的标量元素数为，约束集的维度为，代入即得求解问题式(14)的复杂度。

4 仿真结果与分析

本节通过仿真对算法性能进行验证。本文设计了两种仿真场景，场景1与场景2，分别如图2和图3所示。场景1中基站，中继天线配置为，分别放置于一个边长为的正六边形区域的顶点处。基站与正六边形中心相距400 m，中继6根天线中与基站距离最近的两根天线为接收天线。用户随机分布于距正六边形中心不大于的圆形区域内。场景2中基站，中继天线配置为,网格排布，相邻两天线距离为。基站与网格中心相距400 m，中继9根天线中与基站距离最近的3根天线为接收天线。用户随机分布于距网格中心不大于的圆形区域内。在两种场景中，用户与任意天线的距离不小于10 m。简明起见，集中式处理单元与中继各天线之间的连接未画出。基站和中继的独立功率约束分别为。各链路信道增益由两部分组成，分别对应大尺度和小尺度衰落，小尺度衰落服从独立同分布，大尺度衰落参数参考文献[18]，由表1给出，其中公式中的表示收发天线距离，单位为m。需要注意的是中继-用户链路上的大尺度衰落分为视距(Line-Of-Sight, LOS)和非视距(Non-Line-Of-Sight, NLOS)两种情况给出，取决于与距离相关的LOS概率。。

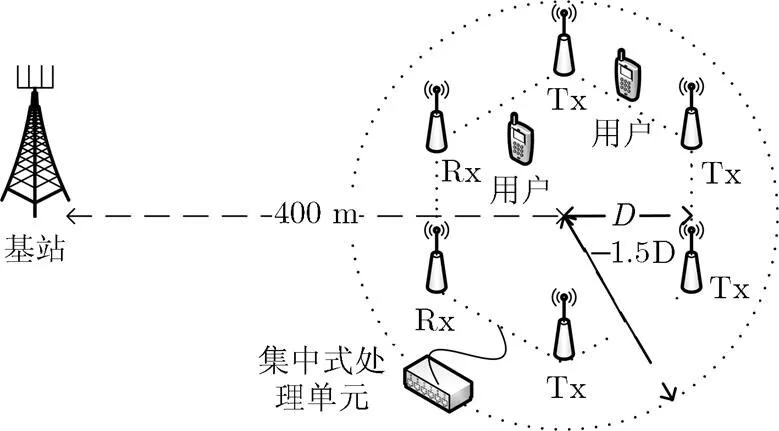
图2 场景1示意图

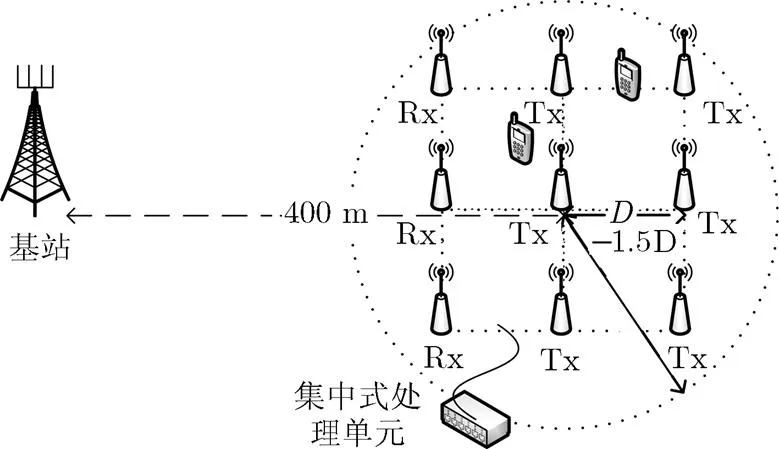
图3场景2示意图

表1大尺度衰落参数

参数公式 基站-中继/自干扰链路损耗(dB) 中继-用户链路LOS概率 中继-用户链路LOS链路损耗(dB) 中继-用户链路NLOS链路损耗(dB)

图4给出了场景1中不同方案下系统频谱效率与分布式天线距离的关系曲线。参考文献[8]，。从图中可以发现，分布式天线距离对系统频谱效率有一定影响，除文献[10]方案外，频谱效率随着的增加而下降。这表明为了获得更高的频谱效率，中继分布式天线间的距离不应过大。对于文献[10]的单用户方案，频谱效率随的变化是非单调的，这是因为文献[10]方案中的基站和中继均以最大功率传输，随着的增加，自干扰减弱，基站-中继链路上传输速率递增；与此同时中继-用户链路上接收信号强度下降，第2跳传输速率递减。由于端到端速率是两跳速率的较小者，因此在时出现一个峰值。与之相比，算法1能够在自干扰严重时，利用波束成形对其进行有效抑制，以维持两跳链路速率的平衡，从而获得更高的频谱效率。

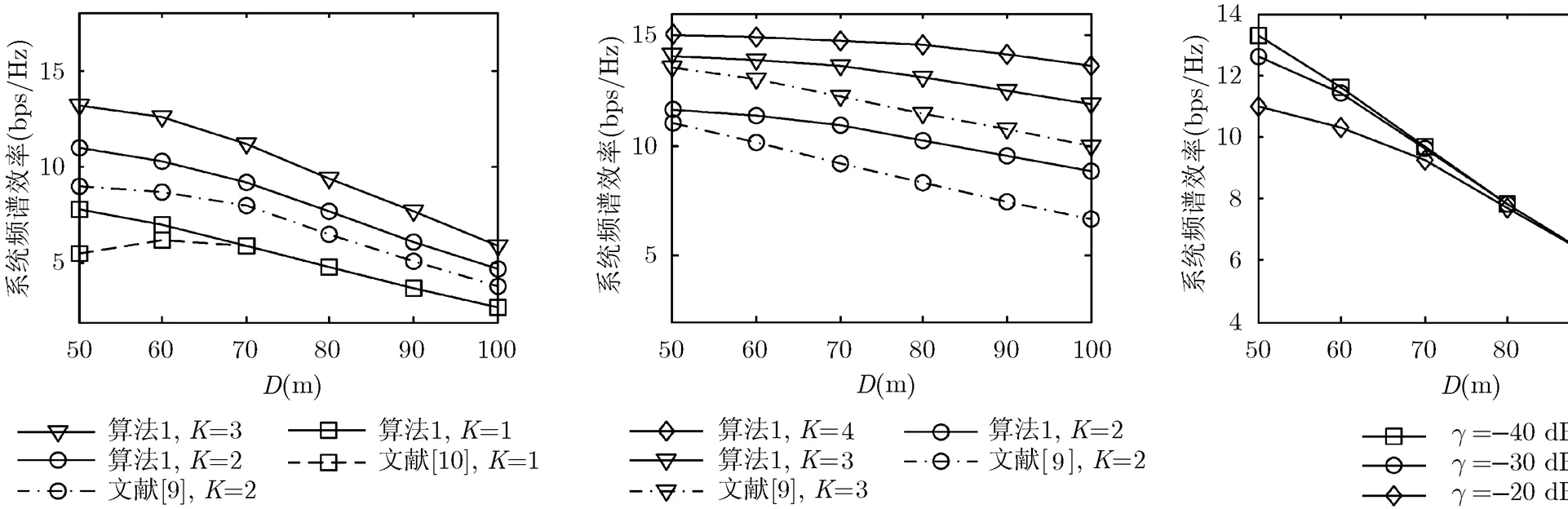
图4 场景1中不同方案下        图5 场景2中不同方案下        图6 场景1中算法1在不同取

系统频谱效率与的关系         系统频谱效率与的关系        值时系统频谱效率与的关系

5 结论

本文在基于分布式天线的全双工中继系统中，提出利用波束成形对自干扰和多用户干扰进行联合抑制，以提高系统频谱效率。提出的双层迭代算法能够在基站和中继天线独立功率约束下，对系统端到端和速率进行优化，并给出相应的波束成形矢量/矩阵。仿真结果表明所提方案能够对自干扰和多用户干扰进行有效的联合抑制，实现多用户场景下的高效传输，明显提高系统频谱效率。

[1] Laneman J N, Tse D N C, and Wornell G W. Cooperative diversity in wireless networks: efficient protocols and outage behavior[J]., 2004, 50(12): 3062-3080.

[2] Xu W, Dong X, and Lu W S. Joint precoding optimization for multiuser multi-antenna relaying downlinks using quadratic programming[J]., 2011, 59(5): 1228-1235.

[3] 李敏, 林敏. 同信道干扰条件下的多天线放大转发中继中断概率分析[J]. 电子与信息学报, 2015, 37(1): 163-168.

Li Min and Lin Min. Outage probability analysis of dual-hop MIMO amplify-and-forward relaying with multiple co-channel interferences[J].&, 2015, 37(1):163-168.

[4] Sabharwal A, Schniter P, Guo D,.. In-band full-duplex wireless: challenges and opportunities[J]., 2014, 32(9): 1637-1652.

[5] Liu G, Yu R, Ji H,.. In-band full-duplex relaying: A survey, research issues and challenges[J].&, 2015, 17(2): 500-524.

[6] 王俊, 赵宏志, 卿朝进, 等. 同时同频全双工场景中的射频域自适应干扰抵消[J]. 电子与信息学报, 2014, 36(6): 1435-1440.

Wang Jun, Zhao Hong-zhi, Qing Chao-jin,.. Adaptive self-interference cancellation at RF domain in co-frequency co-time full duplex systems[J].&, 2014, 36(6): 1435-1440.

[7] Day B P, Margetts A R, Bliss D W,.. Full-duplex MIMO relaying: Achievable rates under limited dynamic range[J]., 2012, 30(8): 1541-1553.

[8] Cirik A C, Rong Y, and Hua Y. Achievable rates of full-duplex MIMO radios in fast fading channels with imperfect channel estimation[J]., 2014, 62(15): 3874-3886.

[9] Taniguchi T and Karasawa Y. Design and analysis of MIMO multiuser system using full-duplex multiple relay nodes[C]. Proceedings of Wireless Days (WD), Dublin, 2012: 1-8.

[10] Jin H and Leung V C M. Performance analysis of full-duplex relaying employing fiber-connected distributed antennas[J]., 2014, 63(1): 146-160.

[11] Zhang X, Sun Y, Chen X,.. Distributed power allocation for coordinated multipoint transmissions in distributed antenna systems[J]., 2013, 12(5): 2281-2291.

[12] Duarte M, Sabharwal A, Aggarwal V,.. Design and characterization of a full-duplex multiantenna system for WiFi networks[J]., 2014, 63(3): 1160-1177.

[13] Wang T and Vandendorpe L. Successive convex approximation based methods for dynamic spectrum management[C]. Proceedings of IEEE International Conference on Communications (ICC), Ottawa, 2012: 4061-4065.

[14] Nguyen D, Tran L N, Pirinen P,.. Precoding for full duplex multiuser MIMO systems: Spectral and energy efficiency maximization[J]., 2013, 61(16): 4038-4050.

[15] Liang Y, Veeravalli V V, and Poor H V. Resource allocation for wireless fading relay channels: max-min solution[J]., 2007, 53(10): 3432-3453.

[16] Boyd S and Vandenberghe L. Convex Optimization [M]. New York, Cambridge University Press, 2004: 561-623.

[17] Stingl M. On the solution of nonlinear semidefinite programs by augmented Lagrangian methods[D]. [Ph.D. dissertation], Friedrich-Alexander University Erlangen-Nürnberg, 2006.

[18] Yuan Y. LTE-Advanced Relay Technology and Standardization[M]. New York, Springer Science & Business Media, 2012: 9-38.

Sum-rate Maximizing Beamforming Design for Distributed-antenna Based Full-duplex Relay Systems

Xu Xiao-fei①②Chen Xiang③Zhao Ming②Zhou Shi-dong①Wang Jing②

①(,,100084,)②(,,100084,)③(,,510275,)

Distributed antenna based full-duplex relay system is capable of simultaneous transmission and reception in the same frequency band on two hops, and it provides uniform coverage for cell edge and deep shadow fading areas with increased spectral efficiency. In multiuser scenarios with non-ideal self interference cancellation, beamforming using multiple distributed antennas is proposed to suppress self interference and multiuser interference jointly. A system model for multiuser end-to-end sum-rate maximization under individual power constraints at distributed antennas is established first. Then, a dual-layer iterative algorithm is proposed to resolve the non-convexity of the problem. Simulation results validate the effectiveness of the proposal algorithm, showing that the proposed beamforming design can be used in distributed-antenna based full-duplex relay systems, to suppress both self interference and multiuser interference efficiently, and increase system spectral efficiency significantly.

Full-duplex relay; Distributed antenna; Beamforming; Interference suppression; Sum-rate

TN929.5

A

1009-5896(2015)11-2657-07

10.11999/JEIT150450

2015-04-20；改回日期：2015-07-08；

2015-08-28

陈翔chenxiang@mail.sysu.edu.cn

国家973计划项目(2012CB316002)；国家863计划项目 (2014AA01A707)；国家重大专项(2014ZX03003003-002)；国家自然科学基金(61201192)；华为科研合作项目

The National 973 Program of China (2012CB 316002); The National 863 Program of China (2014AA01A707); The National S&T Major Project (2014ZX03003003-002); The National Natural Science Foundation of China (61201192); Huawei Technologies

徐霄飞： 男，1988年生，博士生，研究方向为全双工中继网络.

陈 翔： 男，1980年生，博士，副教授，主要研究方向为无线移动通信.

赵 明： 男，1972年生，博士，教授，主要研究方向为无线移动通信.

[1])这里利用了问题式(10)中在上的连续性[15]