基于压缩感知和三次相位变换的低复杂度空中机动目标参数估计

李 海 郑景忠 周 盟 吴仁彪



基于压缩感知和三次相位变换的低复杂度空中机动目标参数估计

李 海*①②郑景忠①周 盟①吴仁彪①

①(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)②(澳大利亚伍伦贡大学电气计算机与通信工程学院 伍伦贡 999029)

该文提出一种基于压缩感知(Compressive Sensing, CS)和三次相位变换(Cubic Phase Transform, CPT)的低复杂度空中机动目标参数估计方法。首先利用CPT将机动目标回波信号中的两个参数进行分离，然后采用压缩感知技术完成机动目标参数的估计。在机载雷达发射脉冲数有限的情况下，该方法能够获得准确的参数估计结果；仿真实验验证了该方法有效性。

机动目标；参数估计；压缩感知；三次相位变换

1 引言

现代战争环境十分复杂，要求情报系统能更好、更快地提供更丰富的情报信息，高性能机载雷达成为不可或缺的技术装备之一[1]。机载相控阵雷达以飞机作为载体，较传统地基雷达，其覆盖范围更大、探测距离更远、生存能力和抗电子干扰能力更高、更加机动灵活，因而受到了日益广泛的重视。但由于载机平台的运动，机载相控阵雷达的地杂波谱在多普勒域上表现为主杂波展宽和旁瓣杂波扩散，导致目标常常淹没在强杂波背景中，目标检测能力受到严重影响[2]。空时2维自适应处理(Space-Time Adaptive Processing, STAP)作为一种有效的机载相控阵雷达地杂波抑制手段，其应用范围越来越广泛。然而STAP是基于平稳信号模型的，即假定在相干处理时间(Coherent Processing Interval, CPI)内目标回波多普勒频率恒定[6](目标为匀速运动)。当来袭目标具有很强的机动性时，其回波多普勒频率随时间变化，使得传统的STAP方法相参积累性能降低，导致目标检测能力下降[7]。

对于加速度恒定的机动目标，其回波信号为线性调频(Linear Frequency Modulation, LFM)信号[8]。近年来，基于各种时频分析工具的LFM信号检测与参数估计的方法不断出现，包括短时傅里叶变换[9](Short Time Fourier Transform, STFT)，小波变换(Wavelet Transform, WT)[10]和分数阶傅里叶变换(FRactional Fourier Transform, FRFT)[11]等。STFT是利用滑动窗函数对Fourier变换进行的扩展，但STFT的观察窗较窄，导致时频域分辨率不高。小波变换需要选择合适的母小波，在实际中很难找到一个标准的母小波能够适应不同环境，一般都是基于经验选取，并且处理过程比较复杂。FRFT是一种广义的傅里叶变换方法，它将信号分解在分数阶傅里叶域的一组正交的chirp基上，而且可借助FFT(Fast Fourier Transform)快速实现，在地基雷达和合成孔径雷达(SAR)中应用比较广泛[12]。然而对机载雷达来说，一个CPI内脉冲数相对有限；在脉冲重复频率(Pulse Repetition Frequency, PRF)一定的条件下，信号的积累时间变短，使得上述方法的机动目标检测能力变差以及参数估计精度降低。文献[13]提出一种基于重构时间采样的机动目标检测和参数估计方法，在脉冲数有限的情况下，能够获得较高的参数估计精度。但是该方法需要对初速度和加速度空间进行2维搜索，运算量较大。上述方法都是基于奈奎斯特采样定理的要求对信号进行采样，当采样频率降低时，这些方法的参数估计性能将下降。

近年来，Candes等人[14]提出了一种新的信息获取指导理论，即压缩感知(Compressive Sensing, CS)。该理论能够保证在不损失信号信息的情况下，用低于奈奎斯特采样定理要求的频率对信号进行采样和压缩，又可以实现信号的重构[15]。文献[16]利用压缩感知方法实现了对机动目标的参数估计，但是该方法需要利用待估参数的先验信息，当先验信息未知时需扩大初速度和加速度的搜索范围，此时构造的2维冗余字典维数急剧增加，导致该算法的运算量大大提高。

本文充分利用机动目标回波信号在时频域的稀疏特性，提出一种基于压缩感知和CPT(Cubic Phase Transform)的低复杂度空中机动目标参数估计方法，该方法利用三次相位变换[17]CPT分离原回波信号中含加速度信息部分，再采用压缩感知方法完成对机动目标的参数估计。仿真实验表明，本文方法相比于重构时间采样方法和文献[16]所提方法，算法的复杂度大幅度地降低；尤其在机载雷达发射脉冲数有限的情况下，仍然能够获得较高的参数估计精度，其优越性更加明显。

2 机动目标回波信号模型

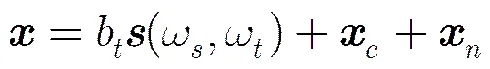
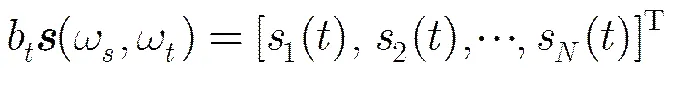
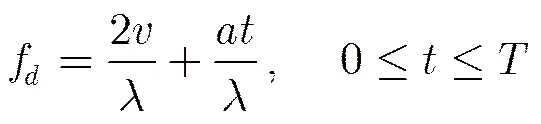
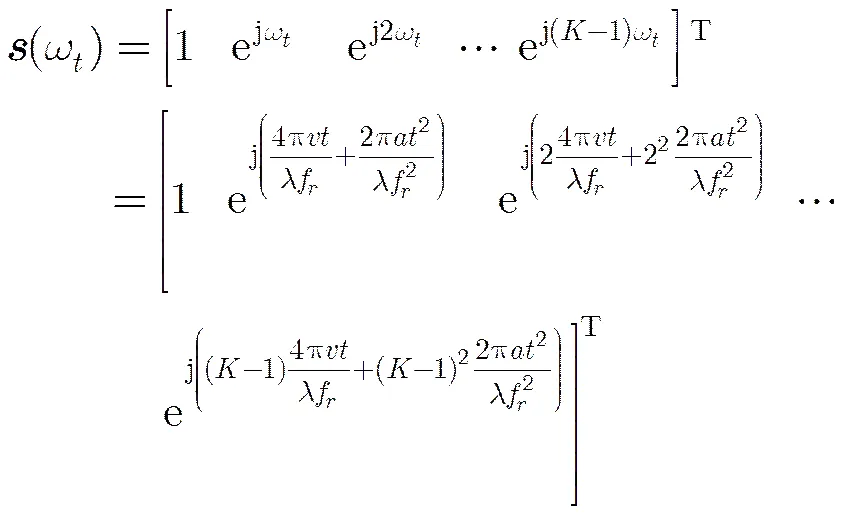
3 基于压缩感知和CPT的低复杂度空中机动目标参数估计方法

本文充分利用机动目标回波信号在时频域具有的稀疏特性，提出了一种基于压缩感知和CPT的低复杂度空中机动目标参数估计方法，首先利用CPT将原回波信号中的初速度和加速度两个参数进行分离，然后再根据机动目标回波信号特点建立过完备冗余字典，采用CS技术分别估计这个两个参数。

3.1算法原理

首先，采用CPT将机动目标加速度引起的二次多普勒信息分离出来。

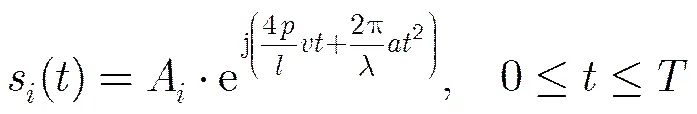
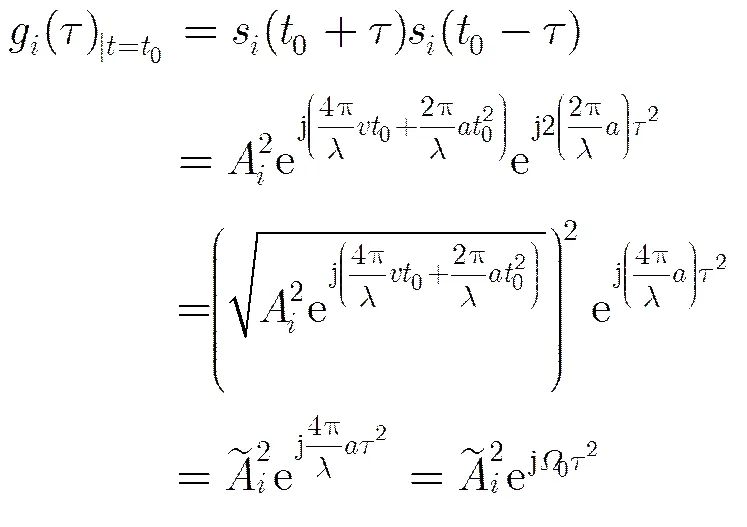
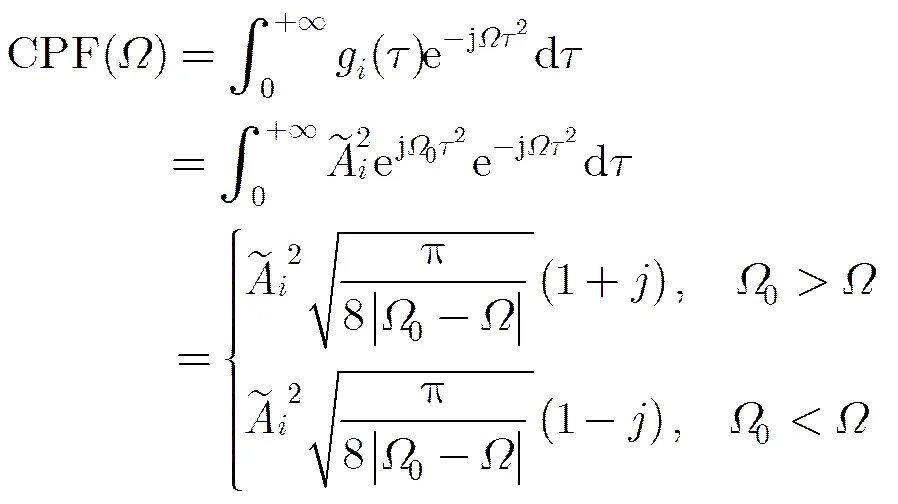
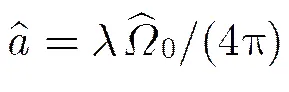
当CPI内发射脉冲数较多时，可利用上述方法估计加速度。但机载相控阵雷达在CPI内发射脉冲数有限，用上面的方法求解加速度时可用数据较少，会导致参数估计精度下降[7]。为了解决发射脉冲数较少时加速度估计精度不高的问题，我们可利用机动目标回波信号在时频域具有稀疏性的特点[8]，采用压缩感知技术对进行求解。

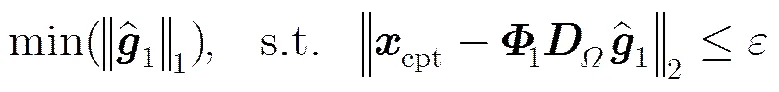
最后，利用上面得到的加速度估计值对杂波抑制后信号进行解调频处理，得到只含有初速度信息的信号，再采用压缩感知完成对初速度的估计。

由加速度的估计值，可得到对机动目标解调频处理的加速度补偿向量为

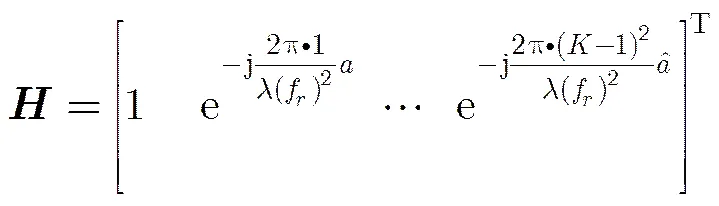
则解调频后的信号可表示为

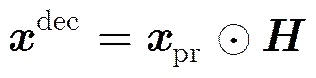
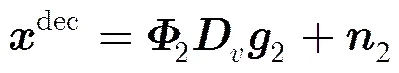
3.2 算法步骤

本文算法原理图如图1所示，具体操作步骤如下：

步骤1 对雷达接收到的待检测单元内总回波信号进行杂波抑制，得到杂波抑制后的信号[20]：

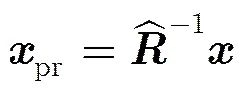
步骤2 对杂波抑制后信号利用CPT变换分离机动目标加速度，采用压缩感技术估计加速度；

步骤3 利用步骤2中估计的加速度对杂波抑制后数据进行解调频处理，再采用压缩感知技术完成初速度的估计。

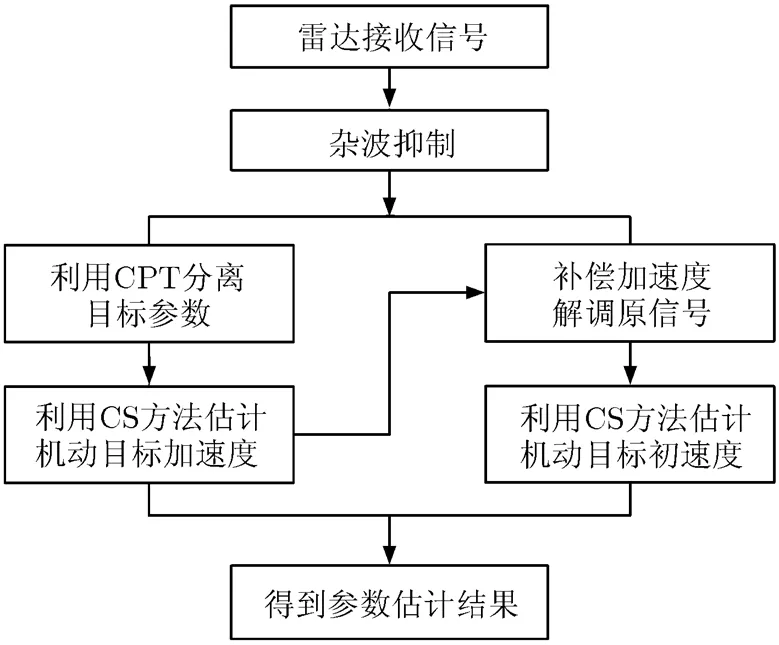
图1 算法原理图

4 仿真结果及分析

本节通过仿真实验来验证本文方法的有效性。仿真参数设置：天线阵为阵元数的均匀线阵，阵元间隔。载机速度，雷达工作波长，平台高度，雷达的距离分辨率，脉冲重复频率，输入信噪比，杂噪比。空中机动目标处于待检测单元内，位于方位角处，初速度为，加速度为，蒙特卡罗实验次数。

图2和图3分别给出了目标参数估计性能与信噪比的变化关系，并给出相应的CRB(Cramer-Rao Bound)理论曲线。

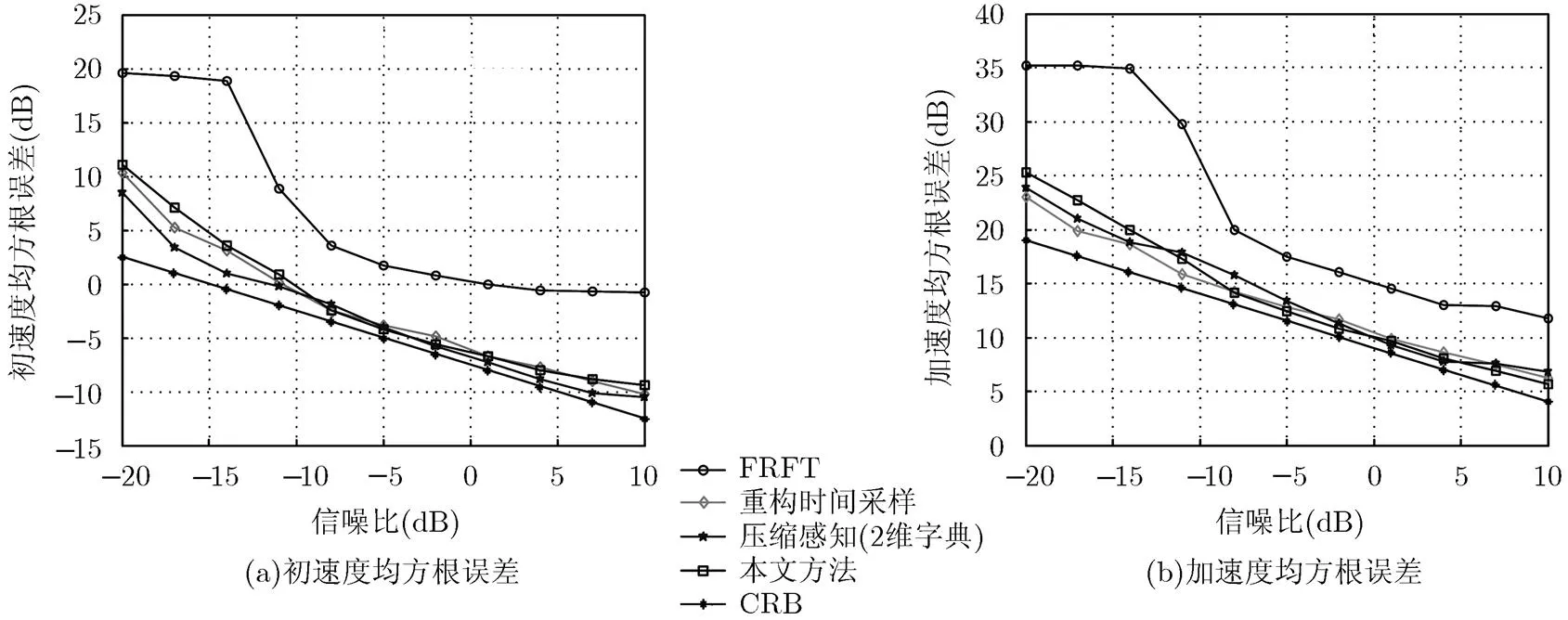
图2 目标参数均方根误差随信噪比变化图(K=64)

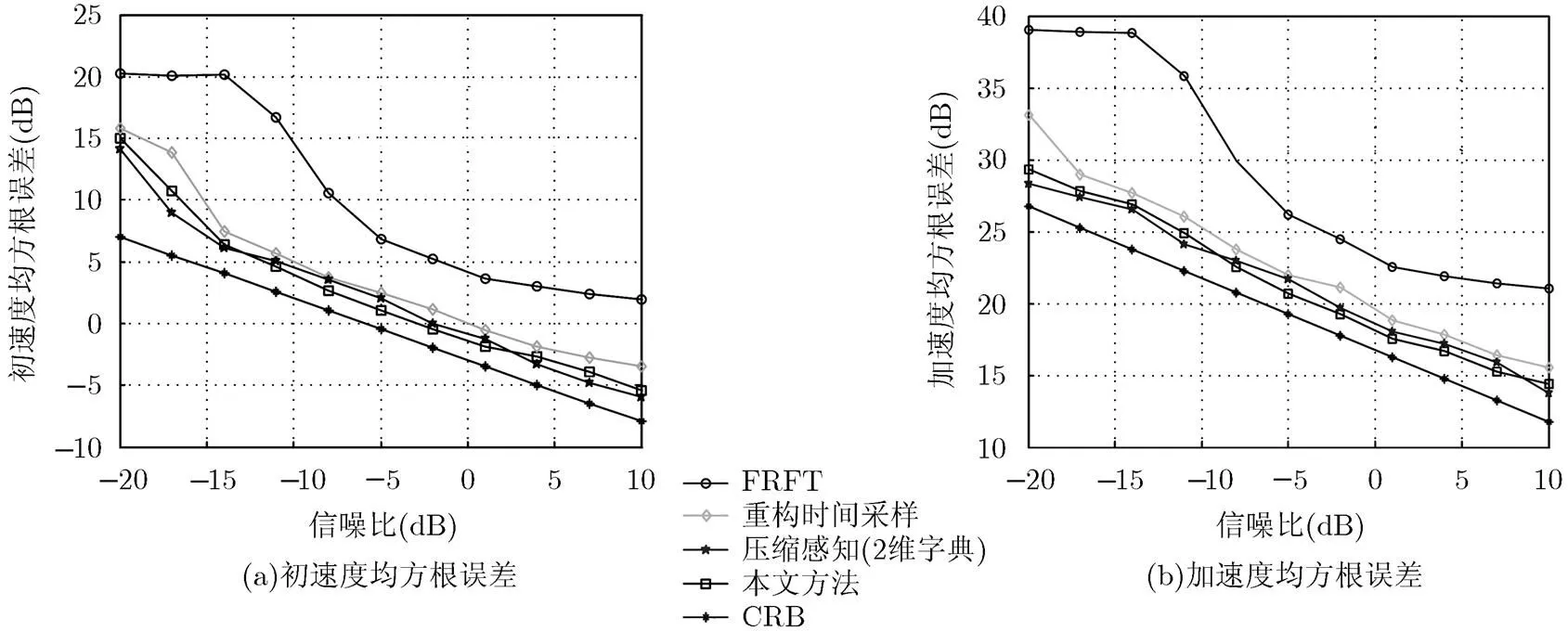
图3 目标参数均方根误差随信噪比变化图(K=32)

图4为当PRF存在10 Hz随机抖动和PRF理想恒定两种情况下(,)，目标参数均方根误差随信噪比变化曲线图，可以看出，当脉冲重复频率存在10 Hz随机抖动时(实际情况中，现代雷达的频率稳定度在量级左右，在文本仿真参数设置中，选择的10 Hz抖动量所占量级约为左右，属于抖动量较大、较为恶劣的情况)，所提算法依然能够较精确地实现机动目标参数估计。

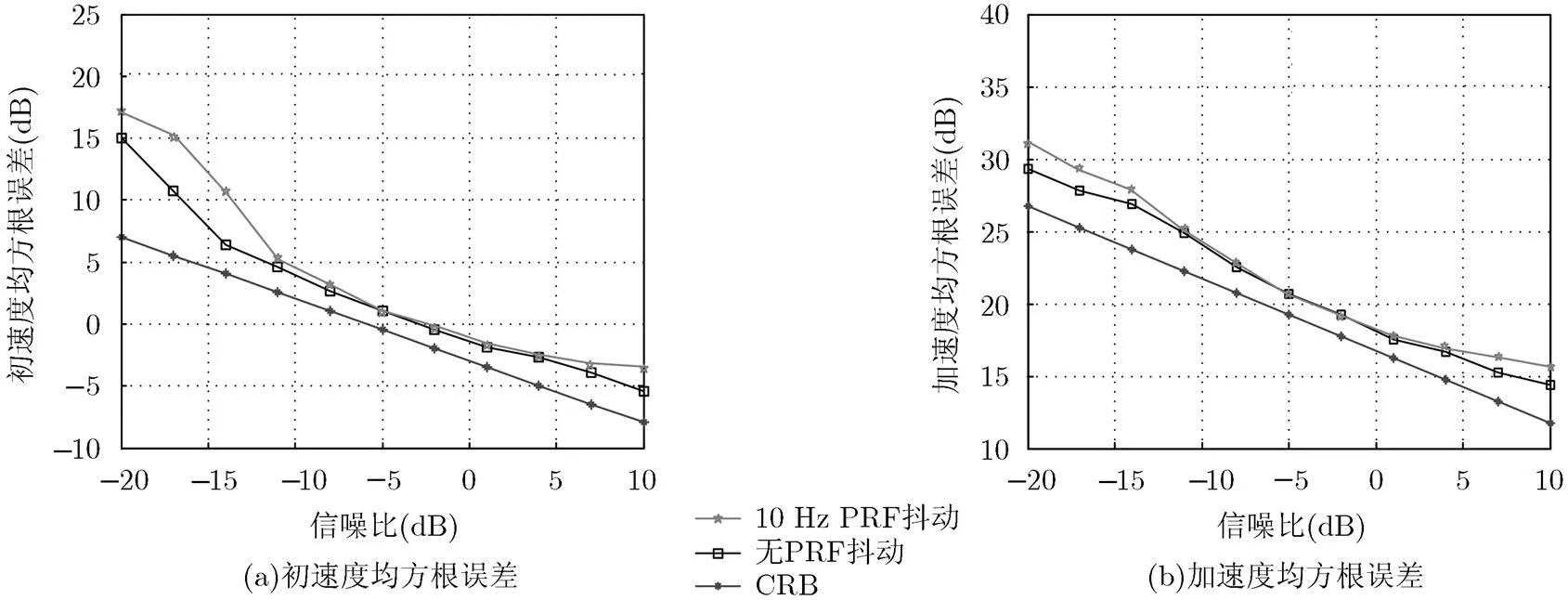
图4 存在PRF抖动时目标参数均方根误差随起伏量变化图(K=32)

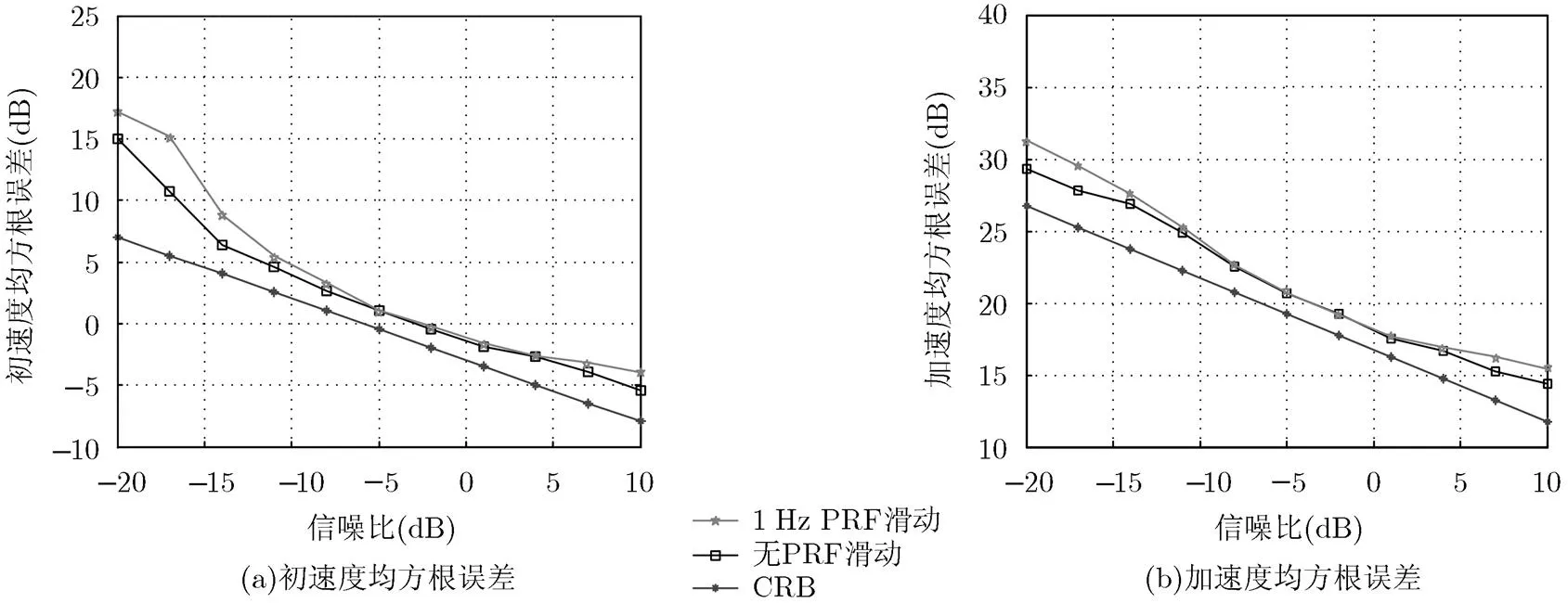
图5 存在PRF滑动时目标参数均方根误差随起伏量变化图(K=32)

图5为当PRF存在+1 Hz滑动时和PRF理想恒定两种情况下(,)，目标参数均方根误差随信噪比变化曲线图，可以看出当脉冲重复频率存在的滑动量为+1 Hz时(实际情况中，现代雷达的频率稳定度在量级左右，本文仿真参数中，1 Hz的频率滑动所占量级约为，属于滑动量较大、较为恶劣的情况)，所提算法的参数估计精度受到的影响较小。

图6为当目标加速度理想恒定以及加速度在真值附近有5%随机起伏情况下，所提算法估计得到的目标参数均方根误差随信噪比变化曲线图()。图7为在信噪比SNR=0 dB时，所提算法估计得到的目标参数均方根误差随加速度起伏量变化图()。可以看出，所提方法处理加速度随机起伏目标结果与处理理想匀加速目标结果相差较小，目标加速度随机起伏对所提算法估计结果影响较小。

图6 加速度5%起伏时目标参数均方根误差随信噪比变化图(K=32)

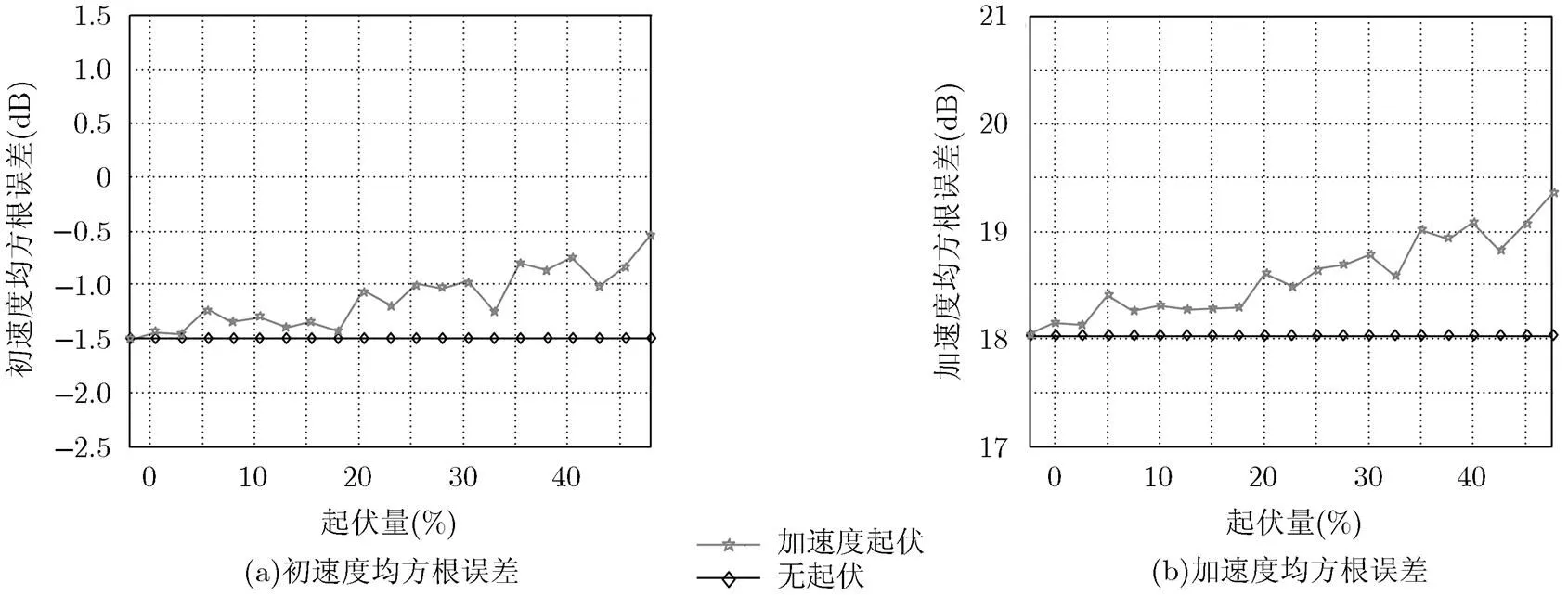
图7 目标参数均方根误差随起伏量变化图(K=32, SNR=0 dB)

表1运算量比较表

算法复乘次数复加次数 重构时间采样 传统2维字典压缩感知 本文方法

5 结束语

本文提出了一种基于压缩感知和CPT的低复杂度空中机动目标参数估计方法，首先利用CPT将关于空中机动目标回波信号参数估计的2维搜索过程转化为两个1维搜索过程，运算量大大降低；然后再根据回波信号的稀疏分解特性，采用压缩感知技术对目标参数进行估计，并将仿真结果分别与基于FRFT和基于重构时间采样方法的估计结果进行比较。结果表明该方法在保证较高参数估计精度的条件下，利用随机测量矩阵用远小于传统采样定理规定的采样速率对回波信号进行采样和压缩，而且采样速率越低时优势越明显。此外，在机载雷达CPI内发射脉冲数有限的情况下，本文方法仍然能够获得准确的参数估计结果，且参数估计性能更接近CRB。

[1] 吴建新. 机载相控阵雷达STAP及目标参数估计方法研究[D]. [博士论文], 西安电子科技大学, 2009.

Wu Jian-xin. Study on space-time adaptive processing and target parameters estimation of airborne phased array radar[D]. [Ph.D. dissertation], Xidian University, 2009.

[2] Yang X P, Liu Y X, and Long T. Performance analysis of optimal and reduced-dimension STAP for airborne phased array radar[C]. 2010 9th International Symposium on Antennas Propagation and EM Theory (ISAPE), Guangzhou, 2010: 1116-1119.

[3] Jean-Francois D, Laurent S, and Sylvie M. Reduced-rank STAP for target detection in heterogeneous environments[J]., 2014, 50(2): 1153-1162.

[4] Li Xao-ming, Feng Da-zheng, Liu Hong-wei,. Dimension-reduced space-time adaptive clutter suppression algorithm based on lower-rank approximation to weight matrix in airborne radar[J]., 2014, 50(1): 53-69.

[5] 蒋浩, 翟雯, 饶妮妮, 等. 基于多级维纳滤波的机载共形阵雷达杂波抑制方法研究[J]. 电子与信息学报, 2014, 36(10): 2477-2483.

Jiang Hao, Zhai Wen, Rao Ni-ni,.. Study on clutter suppression method of airborne conformal array radar based on multistage wiener filter[J].&, 2014, 36(10): 2477-2483.

[6] Hayward S D. Principle of space-time adaptive processing[J].&, 2002, 14(6): 295-296.

[7] 刘建成. 加速运动目标检测及跟踪技术研究[D]. [博士论文], 国防科学技术大学, 2007.

Liu Jian-cheng. Study on accelerating target detection and tracking[D]. [Ph.D. dissertation], National University of Defense Technology, 2007.

[8] 贾舒宜, 王国宏, 张磊. 基于压缩感知的机动目标径向加速度估计[J]. 系统工程与电子技术, 2013, 35(9): 1815-1820.

Jia Shu-yi, Wang Guo-hong, and Zhang Lei. Radial acceleration estimation of maneuvering target based on compressive sensing[J].,2013, 35(9): 1815-1820.

[9] Oberlin T, Meignen S, and McLaughlin S. Analysis of strongly modulated multicomponent signals with the short-time Fourier transform[C]. 2013 IEEE International Conference on Acoustics, Speech, and Signal Processing, Vancouver, Canada, 2013: 1558-1564.

[10] Ma N and Wang J X. Wide band LFM signal parameter estimation based on compressed sensing theory[C]. 3rd International Conference on Manufacturing Engineering and Process, ICMEP 2014, Seoul, Korea, 2014: 1160-1165.

[11] Singh K, Saxena R, and Kumar S. Caputo-based fractional derivative in fractional Fourier transform domain[J]., 2013, 3(3): 330-337.

[12] 陈小龙, 刘宁波, 王国庆, 等. 基于Radon-分数阶傅里叶变换的雷达动目标检测方法[J]. 电子学报, 2014, 42(6): 1074-1080.

Chen Xiao-long, Liu Ning-bo, Wang Guo-qing,Radar detection method for moving target based on Radon-Fourier fractional Fourier transform[J]., 2014, 42(6): 1074-1080.

[13] 吴仁彪, 王小寒, 李海, 等. 基于重构时间采样的空中机动目标检测与参数估计[J]. 电子与信息学报, 2012, 34(4): 936-942.

Wu Ren-biao, Wang Xiao-han, Li Hai,Detection and parameter estimation of air maneuvering targets via reconstructing time samples[J].&, 2012, 34(4): 936-942.

[14] Candes E J and Wakin M B. An introduction to compressive sampling: a sensing/sampling paradigm that goes against the common knowledge in data acquisition[J]., 2008, 25(2): 21-30.

[15] 王超宇, 贺亚鹏, 朱晓华, 等. 基于贝叶斯压缩感知的噪声MIMO雷达稳健目标参数提取方法[J]. 电子与信息学报, 2013, 35(10): 2498-2504.

Wang Chao-yu, He Ya-peng, Zhu Xiao-hua,A robust target parameter extraction method via Bayesian compressive sensing for noise MIMO radar[J].&, 2013, 35(10): 2498-2504.

[16] 贾琼琼, 吴仁彪. 基于压缩感知的空时自适应动目标参数估计[J]. 电子与信息学报, 2013, 35(11): 2714-2720.

Jia Qiong-qiong and Wu Ren-biao. Space time adaptive parameter estimation of moving target based on compressed sensing[J].&, 2013, 35(11): 2714-2720.

[17] O’ Shea P. A fast algorithm for estimating the parameters of a quadratic FM signal[J]., 2004, 52(2): 385-393.

[18] 赵光辉, 张天键, 沈方芳, 等. 低信噪比下稳健压缩感知成像[J]. 航空学报, 2012, 33(3): 561-572.

Zhao Guang-hui, Zhang Tian-jian, Shen Fang-fang,Robust compressive sensing SAR imaging in low SNR condition[J].,2012, 33(3): 561-572.

[19] 夏建明, 杨俊安, 陈功. 参数自适应调整的稀疏贝叶斯重构算法[J]. 电子与信息学报, 2014, 36(6): 1355-1361.

Xia Jian-ming, Yang Jun-an, and Chen Gong. Bayesian sparse reconstruction with adaptive parameters adjustment[J].&, 2014, 36(6): 1355-1361.

[20] 郭佳佳, 廖桂生, 杨志伟, 等. 利用广义内积值迭代加权的空时协方差矩阵估计方法[J]. 电子与信息学报, 2014, 36(2): 422-427.

Guo Jia-jia, Liao Gui-sheng, Yang Zhi-wei,. Iterative weighted covariance matrix estimation method for STAP based on generalized inner products[J].&, 2014, 36(2): 422-427.

Parameters Estimation of Air Maneuvering Target Based on Compressive Sensing and Cubic Phase Transform

Li Hai①②Zheng Jing-zhong①Zhou Meng①Wu Ren-biao①

①(,,300300,)②(,,,,999029)

A novel and low complexity algorithm is proposed to estimate the parameters of air maneuvering target based on Compressive Sensing (CS) and Cubic Phase Transform (CPT). First of all, CPT is utilized to separate the two parameters of the maneuvering target. Then, CS is used to estimate the parameters according to the properties of sparse signal in the time-frequency domain. The proposed algorithm can acquire precise parameter estimation with limited pulses in a coherent processing interval for airborne radar. The effectiveness of the proposed algorithm is verified by the numerical simulations.

Maneuvering target; Parameter estimation; Compressive Sensing (CS); Cubic Phase Transform (CPT)

TN957.51

A

1009-5896(2015)11-2697-08

10.11999/JEIT150170

2015-01-29；改回日期：2015-07-21；

2015-08-27

李海 haili@cauc.edu.cn

国家自然科学基金(61471365, 61231017)；中国民航大学蓝天青年学者培养经费；中央高校基本科研业务费项目(3122015B002)

The National Natural Science Foundation of China (61471365, 61231017); Foundation for Sky Young Scholars of Civil Aviation University of China; The Fundamental Research Funds for the Central Universities (3122015B002)

李 海： 男，1976年生，副教授，主要研究方向为机载气象雷达信号处理、动目标检测、干涉合成孔径雷达信号处理等.

郑景忠： 男，1988年生，硕士生，研究方向为动目标检测与估计、空时自适应信号处理等.

周 盟： 男，1988年生，硕士生，研究方向为动目标检测、机载气象雷达信号处理.

吴仁彪： 男，1966年生，教授，博士生导师，主要研究方向为自适应阵列信号处理、探地雷达信号处理、高分辨率雷达成像与自动目标识别、民航无线电干扰检测与自适应抑制等.