轨下垫板刚度的时变特性及其影响研究

张 攀，周昌盛，王 平

(1.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；2.西南交通大学土木工程学院，成都 610031)

轨下垫板刚度的时变特性及其影响研究

张 攀1，2，周昌盛1，2，王 平1，2

(1.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；2.西南交通大学土木工程学院，成都 610031)

以WJ7-A型轨下垫板为对象，测试轨下胶垫刚度随服役时间的变化，分析垫板刚度的时变特性；然后以此为基础，建立车辆-轨道垂向耦合动力学模型，研究轨下胶垫时变特性对轮轨随机振动响应的影响规律。研究结果表明：随着服役时间的增长，轨下橡胶垫板的刚度将增大，2年后垫板刚度的增幅为13.91%；随着运营时间的增长，车体振动加速度变化微弱；轮轨力及扣件力的第二主频幅值增大并向高频移动，且扣件力变化更显著，线路运营2年时间后，扣件力第二主频向高频移动7.4 Hz，幅值增幅达到53.80%。建议定期抽样测试轨下胶垫刚度并及时更换性能老化垫板，降低轮轨垂向力和扣件力。

无砟轨道；高速铁路；轨下垫板；随机振动

1 概述

由于无砟轨道具有高稳定性、高平顺性和少维修性的特点，世界各国的高速铁路竞相发展无砟轨道[1]。随着客运专线和高速铁路的修建，无砟轨道更显现出其优越性和重要性[2-3]。截至2014年底，我国高速铁路总运营里程达到1.6万km，大部分线路采用无砟轨道结构[4-5]。

扣件系统是无砟轨道的关键结构之一，其中的轨下垫板更是为无砟轨道结构提供了大部分的弹性[6-7]。轨下垫板由粘弹性高分子材料制成，其刚度将随温度和时间发生改变，进而影响轮轨系统的受力特点。因此，研究垫板刚度随运营时间的变化规律，进而研究无砟轨道上轮轨系统随机振动响应随时间的变化规律，对线路的养护维修具有重要意义。

为此，本文在现场随机抽取几组服役2年后的WJ7-A型轨下垫板，测试其刚度，并与同型号新垫板的刚度进行对比，研究轨下垫板刚度的时变特性。另外，基于车辆-轨道垂向耦合模型，研究了轮轨系统随机振动响应的时变特性，以期为无砟轨道扣件垫板的养护维修提供一定的指导。

2 轨下垫板的时变特性试验

2.1 试验设备及试件准备

加载设备选用WDW系列微机控制电子万能材料试验机，该设备采用计算机控制，伺服电机驱动，精密滚珠丝杠机械加载，传感器测量信号，经过信号转换成数字信号后由计算机采集，位移测量精度能达到0.001 mm。其他试验材料还有短钢轨，支承钢板，砂布等。

试验所用试件分为2组，一组是全新的未使用过的WJ7-A型垫板(简称“新垫板”)，另一组是现场已使用2年的WJ7-A型垫板(简称“旧垫板”)，每组试件至少试验3块垫板，以保证试验数据的有效性，测试试件如图1所示。

图1 WJ7-A型轨下垫板

2.2 试验过程

通过试验机向垫板施加垂向荷载，测定垫板表面在荷载作用下的位移，以此反算垫板静刚度。试验过程可分3个步骤完成。

第一步：试验前将轨下橡胶垫板在23±2 ℃温度范围内放置24 h。

第二步：预加载，对试件加载到140 kN然后卸载，停留1 min，如此反复2次。

第三步：正式试验，以2～3 kN/s速度均匀加载。当荷载加载至20 kN和80 kN时，各停留1 min，并分别记录位移D1i，D2i。如此反复试验3次，计算3次D1i，D2i平均值，记为D1，D2。

静刚度用式(1)计算[8]

(1)

式中F1——向被测橡胶垫板标准试件施加的最小荷载，20 kN；

F2——向被测橡胶垫板标准试件施加的最大荷载，80 kN；

D1——被测橡胶垫板试件在加载至F1时的位移，mm；

D2——被测橡胶垫板试件在加载至F2时的位移，mm；

Ks——胶垫静刚度，kN/mm。

2.3 试验结果及分析

测试得到2组胶垫的静刚度见表1。

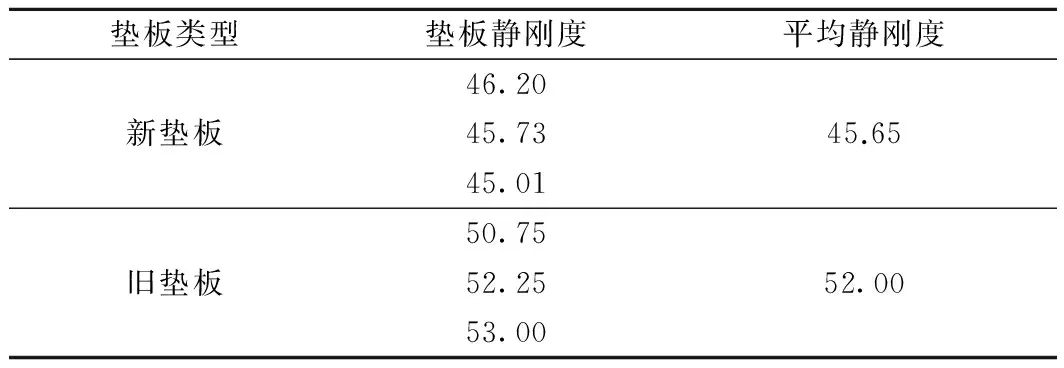
表1 垫板静刚度测试结果 kN/mm

从表1可见，轨下胶垫服役2年后，静刚度平均值由45.65 kN/mm增大到52.00 kN/mm，增加幅度为13.91%。

可见随服役时间的增加，垫板刚度将增大，下文将建立车辆-轨道垂向耦合动力学模型，研究轮轨系统随机振动响应随胶垫刚度时变特性的变化规律。

3 车辆/轨道随机振动模型

3.1 车辆-轨道垂向耦合动力学模型

3.1.1 车辆模型

车辆模型采用全车模型。它能准确地反映车体沉浮(Zc)和点头(βc)运动，前后转向架的沉浮(Zg)和点头(βg)运动，以及4个轮对的垂向运动(Zwj，j=1～4)，共10个自由度[9]。车辆模型的计算参数如表2所示。在表2中Mc，Mt和Mw分别是车体、转向架与一个轮辐的质量；Jc和Jt分别是车体与转向架的点头惯量；Kp和Cp分别是一系悬挂刚度与阻尼；Ks和Cs分别是二系悬挂刚度与阻尼。

表2 车辆模型的计算参数

3.1.2 轨道模型

轨道模型采用长枕埋入式无砟轨道模型。该轨道系统由钢轨、扣件(包括轨下垫板)、混凝土轨枕、混凝土无砟道床板、隔离层及混凝土底座等组成。其中，轨枕与道床板紧密联结在一起，加上轨下基础质量很大，道床板与混凝土底座之间几乎没有弹性，轨道的弹性主要由轨下垫板提供。轨道系统的结构参数如表3。

表3 轨道结构的计算参数

3.2 随机响应分析中的传递函数矩阵

根据经典线性随机理论，输入与输出功率密度函数之间有如下关系

(2)

式中，[H(ω)]为系统振动传递函数矩阵；[H*(ω)]为[H(ω)]的共轭函数矩阵；[H(ω)]T为[H(ω)]的转置函数矩阵。

如果按照上式计算系统输出响应功率谱会十分繁琐，可根据地铁车辆激振特点，将多轮对激励多自由度响应输入输出系统化简为单输入单输出系统，为此文献[10]给出了多自由度的单输入单输出系统的传递函数矩阵

(3)

式中，[Hs(ω)]为振动系统n个轮对激励的m个自由度响应的传递函数矩阵。

(4)

其中，Δl为i轮对与第一轮对的间距；v为车速(m/s)。

3.3 各自由度下的功率密度谱

各自由度下的功率密度谱可由 3.2节得出的传递函数矩阵[Hs(ω)]求解[11]，具体做法如下。

整个系统的振动微分方程可用矩阵形式表达

(5)

其中，M为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；Kf为系统的转换矩阵；Q为系统广义力向量；q为系统广义位移向量；Z0为不平顺位移向量。

假定Z0=Ie-jωt，则有q=H(ω)e-jωt，将其代入系统二阶线性微分方程式(5)可求解系统振动传递函数矩阵H(ω)

(6)

由此即可求出传递函数矩阵，于是自由度响应功率谱为

(7)

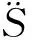
3.4 扣件力的功率密度谱

(8)

于是，扣件力的功率密度谱为

(9)

3.5 轮轨力的功率密度谱

轮轨力大小为P0j(t)=Kh[Zw(j，t)-Zr(j，t)-(j，t)]。其中，Zw(j，t)为第j个轮对的垂向位移；Zr(j，t)为第j个轮对对应钢轨的位移；(j，t)为第j个轮对对应钢轨处的不平顺。

由轮对位移，轮对对应位置处钢轨垂向位移的频响函数及不平顺激励，可得轮轨力的频响函数HP2(ω)

(10)

于是，轮轨力的功率密度谱为

(11)

4 对轮轨系统的影响

随机振动过程中，轨下垫板动刚度反映系统的动力特性。研究表明，我国自主研制的轨下垫板的动静刚度比一般在1.5左右[12]。取新旧橡胶垫板的动静刚度比均为1.5，则新旧垫板的动刚度分别为68.47 kN/mm及78.00 kN/mm。随机振动过程中，不平顺激励采用美国六级谱，列车速度取200 km/h。

4.1 对车体加速度的影响

新旧垫板支承作用下车体的垂向加速度功率谱如图2所示。

图2 车体加速度功率谱

从图2可见，车体的垂向加速度响应在低频范围内保持稳定而在高频范围内幅值有微小差异，但变化微小，可以忽略不计。轨下垫板刚度的变化对车体的振动响应的影响很小，当橡胶垫板刚度发生一定变化时，并不会影响行车舒适性。

4.2 对轮轨力的影响

新旧垫板支承作用下轮轨垂向力频谱如图3所示。

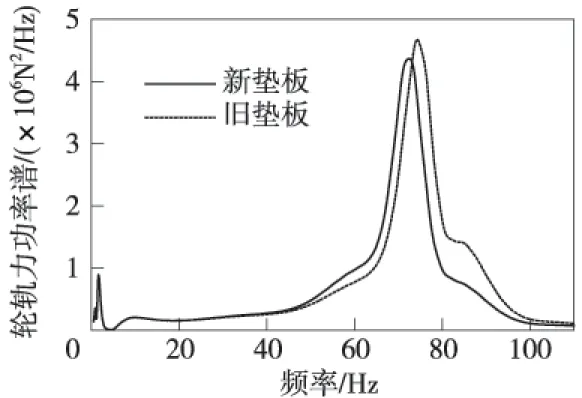
图3 轮轨垂向力功率谱

从图3可见，在旧垫板支承作用下，轮轨力的第二主频幅值增大，且第二主频向高频转移。第二主频幅值增幅为7.06%，主频从72.39 Hz移动到了74.29 Hz。环境因素对轨下垫板性能产生影响的同时，轮轨接触处的受力情况随着发生变化，随着时间的增长，轮轨力有增大的趋势，轮轨接触振动向高频发展。

4.3 对扣件力的影响

新旧垫板支承作用下扣件力功率谱如图4所示。

图4 扣件力功率谱

从图4可见，旧垫板支承作用下，扣件力的幅值增大，第二主频向高频转移。第二主频幅值增幅为53.80%，第二主频由70.26 Hz转移到了77.70 Hz。因此，环境因素对轨下垫板性能产生影响的同时，扣件力发生显著变化。

扣件力通过轨下结构传递到路基及附近环境当中，是环境振动的激励源。随着时间的推进，列车经过引起的环境振动会明显的增强，而振动的范围将向高频方向转移。

综上所述，考虑轨下垫板刚度时变性时，随着时间的增长，车体振动响应发生微小变化，轮轨接触力及扣件力的大小及分布将发生变化，且扣件力所受影响最大。在研究环境振动过程中需考虑轨下胶垫的时变特性。

5 结论及建议

本文针对全新及现场取样的WJ7-A型轨下垫板，测试其静刚度，研究了轨下胶垫的时变特性，进而分析了随着服役时间变化轮轨系统随机振动响应的差别，研究结果表明：

(1)随着服役时间增加，轨下橡胶垫板的刚度将增大；在使用2年后，轨下垫板的刚度平均由45.65 kN/mm增大到52.00 kN/mm，增幅为13.91%；

(2)轨下胶垫的时变特性对车体振动加速度影响较小，对行车舒适性基本无影响；

(3)随着时间的推进，轮轨力及扣件力第二主频幅值增大并向高频移动，特别是扣件力，线路运营2年时间后，扣件力第二主频由70.26 Hz转移到77.70 Hz，幅值增幅达到53.80%；

(4)对无砟轨道进行线路养护维修时，需特别注意检查轨下垫板的性能，如有条件应进行定期抽样测试；及时更换性能老化垫板，能够减小轮轨接触力及扣件力，进而在延长列车轮对及钢轨使用寿命的同时，减小传递到轨下结构及周围环境的振动。

(5)本文所用全新与现场取样的WJ7-A型轨下垫板是同型号不同批次生产的。用全新垫板的静刚度值代替取样垫板两年前的静刚度值可能存在一定差异，这是本文的不足之处。

[1]全顺喜，魏贤奎，王平.无砟轨道高低和方向不平顺控制方法探析[J].铁道标准设计，2012.

[2]李成辉.轨道[M].成都:西南交通大学出版社，2007.

[3]何华武.无砟轨道技术[M].北京:中国铁道出版社，2005.

[4]姜浩，赵坪锐，刘观.减振型无砟轨道轨枕结构对比分析[J].铁道标准设计，2014(10)：51-56.

[5]田春香，颜华，熊维.关于高速铁路扣件间距的探讨[J].铁道标准设计，2013(8)：32-36.

[6]刘学毅，张重王，万章博.无砟轨道扣件刚度突变对高速列车动力的影响[J].铁道工程学报，2014(9):53-58.

[7]许佑顶.高速铁路无砟轨道扣件设计要点[J].铁道工程学报，2010(4):40-43.

[8]中华人民共和国铁道部.TB/T 2626.1—1995铁路轨道系统用弹性垫板[S].北京:中国铁道出版社，1995.

[9]翟婉明.车辆-轨道耦合动力学[M].3版.北京: 科学出版社，2007.

[10]陈果.车辆-轨道耦合系统随机振动分析[D].成都:西南交通大学，2000.

[11]韦凯，翟婉明，肖军华.软土地铁盾构隧道垂向随机振动分析模型[J].工程力学，2014.

[12]王鑫，毛昆明，吴智强，等.低动静刚度比的聚氨酯微孔弹性体的研究[J].聚氨酯工业，2011，26(5):19-22.

Study on Time Variant Characteristics and Effects of Rail Pad Stiffness

ZHANG Pan1，2, ZHOU Chang-sheng1，2, WANG Ping1，2

(1.MOE Key Laboratory of High-speed Railway Engineering， Ministry of Education， Chengdu 610031， China；2.School of Civil Engineering， Southwest Jiaotong University， Chengdu 610031， China)

With respect to WJ7-A rail pad， the change of rail pad stiffness with service time is tested and the time variant characteristics of rail pad stiffness are analyzed. The vehicle-track vertical coupling dynamic model is established based on the test results， the effects of time variant characteristics of rail pad stiffness on the random vibration responses of wheel-rail system are studied. The results show that the stiffness of the rail pad increases with the increasing of the service time， and the increase amplitude is about 13.91% after 2 years. The vibration acceleration of vehicle fluctuates slightly with the extension of the operating time. The second dominant frequency of wheel-rail force and fastening force increase and move to a higher frequency and the fastening force changes significantly. After two years of operation， the second dominant frequency of fastening force moves by 7.4Hz to a higher frequency， and the amplitude increases by 53.80%. In order to reduce wheel-rail force and fastening force， it is recommended to test regularly the stiffness of the rail pad by sampling and replace the aging pads timely.

Ballastless track; High speed railway; Rail pad; Random vibration

2014-12-15；

2014-12-30

国家自然科学基金高铁联合基金项目(U1234201)；四川省科技支撑计划项目(2014GZ0003)。

张 攀(1992—)，男，硕士研究生，E-mail:1310652582@qq.com。

1004-2954(2015)09-0049-04

U213.5+32

A

10.13238/j.issn.1004-2954.2015.09.012