基于SLR与L波段同步观测解算北斗卫星钟差

胡佳钰,韩兴伟,张子昂

(1.中国科学院国家天文台长春人造卫星观测站,吉林 长春 130117； 2.中国科学院大学,北京 100049)



·激光应用技术·

基于SLR与L波段同步观测解算北斗卫星钟差

胡佳钰1,2,韩兴伟1,张子昂1

(1.中国科学院国家天文台长春人造卫星观测站,吉林 长春 130117； 2.中国科学院大学,北京 100049)

导航卫星钟差的大小通常在毫秒量级,若不进行精密修正,对卫星导航定位精度的影响很大。本文阐述了综合利用SLR观测值和北斗L波段单频伪距观测值对BDS卫星钟差进行解算的原理和计算方法。采用2014年8月及9月从长春SLR和GNSS并址站采集的激光测距观测值和北斗L波段单频伪距观测值计算了COMPASS-G1的卫星钟差,以GFZ分析中心提供的COMPASS-G1卫星钟差为参考进行对比,互差在6 ns之内,表明使用该方法计算COMPASS-G1卫星钟差是可行的。

卫星激光测距；北斗卫星导航系统；L波段观测值；卫星钟差

1 引 言

北斗卫星导航系统(BeiDou(COMPASS)Navigation Satellite System,BDS)的基本观测量是以时间信号为基准获得的,星地间时间同步误差直接影响到距离观测精度,从而导致导航系统的导航、定位和授时精度下降。星地间时间同步误差中的卫星钟差量级通常为毫秒级别,若不进行精确修正,对定位的影响可达米级。目前,北斗导航系统初步建成了亚太地区导航定位服务网络,全球组网计划将于2020年左右完成。在现阶段卫星数有限的情况下,获取导航卫星的精密轨道和钟差是提升卫星导航系统定位服务能力的关键[1]。求解精密导航卫星钟差,对完善卫星控制系统、实现单点精密定位和卫星定轨具有重要意义。求卫星钟差最常用的方法是组差求解,这种方法需要多个测站的支持,而且因为星地钟差难以完全分离,解算的卫星钟差精度随之降低。目前国内很多专家对导航卫星钟差的解算进行了深入研究,秦显平等提出利用SLR测距数据辅助GPS伪距求卫星钟差,对GPS35卫星进行了卫星钟差求解和预报,效果较好[2]。毛悦等验证了SLR和GPS伪距进行卫星钟差预报的精度[3]。他们的工作证明用SLR观测值和卫星微波数据求GPS卫星钟差的可行性。本文综合利用SLR观测值和北斗卫星L波段单频伪距观测值,进行BDS卫星钟差的计算方法的研究,从而实现单站分离卫星钟差和接收机钟差。BDS二代卫星上全部装有激光后向反射器,并且部分加入了国际卫星激光测距服务组织(ILRS)的国际联测中。长春站于2009年实现了常规白天千赫兹卫星激光测距[4],也是目前国际上8个能够对COMPASS-G1进行观测的台站之一,到目前为止已观测360多圈数据。基于以上条件,本文利用长春站(CHAL)提供的SLR观测值和北斗L波段单频伪距观测值,计算COMPASS-G1的卫星钟差,并与德国波茨坦地学研究中心(GeoForschungsZentrum,GFZ)提供的精密卫星钟差数据进行了对比以分析其外符精度。

2 原理与方法

卫星激光测距(SLR)是一种高精度空间测量手段,它可以精密测量激光从地面观测站到卫星激光反射器之间的往返时间间隔t,则某一时刻测站到卫星的理论距离为：

ρ=cτ/2

(1)

式中,c为光速。

二代北斗卫星导航定位系统(COMPASS)采用单程测量传播延迟的测距原理。由于卫星钟和接收机钟不同步,所以其得到的观测量是含有两个时钟钟差的伪距,它等于所测卫星到接收机的距离加两个钟钟差的修正,忽略掉延迟改正,可写为：

ρ=ρ+cΔtR-cΔts

(2)

式中,ρ为伪距观测量,ρ为卫星到接收机的距离,ΔtR为接收机钟差,Δts为卫星钟差。

由公式(1)可知,SLR可以直接测定卫星到观测站的距离,且不含钟差信息。如果卫星激光测距仪和GNSS接收机采用相同的时钟,在同一位置同一时刻各自测得卫星到观测站的距离,则由式(2)可以得到：

cΔts=ρ+cΔtR-ρ′

(3)

由式(3)可以看出,只要观测站同时具有SLR资料和伪距资料,以及测站钟差,就可以直接获得卫星钟差。

由于SLR和微波测距是两套不同的测距系统,在利用两种观测资料求卫星钟差时,必须进行时刻同步、误差修正和GNSS接收机与SLR测距仪的归心改正三步处理[2]。本文所做具体修正在下文表述。

2.1 SLR数据计算

激光在测站和卫星角反射器之间传播时,会受到各种因素的影响,下面给出激光测距的实际观测模型[5]：

(4)

从式(4)可以看出,卫星激光测距的误差修正包括广义相对论修正,测站固体潮改正,卫星质心补偿改正,测站偏心改正,对流层延迟改正及激光观测噪声等。其中,广义相对论改正约2 cm,改正残余误差在mm量级。激光对流层延迟改正采用的模型为Marini-Murry模型[6],改正残余误差优于1 cm[3]。COMPASS-G1的质心位置在星固系中相对于原点的坐标为(1082.0,-0.4,-0.5) mm,激光反射器相位中心在星固系中相对于原点的坐标为(649.9,-562.5,1133.3) mm,卫星质心补偿改正取0.5m。暂时不考虑相对论改正、测站偏心改正和激光观测噪声的误差影响。SLR观测值经过各项误差改正后的精度可达3 cm。

2.2 北斗L波段伪距数据计算

BDS采用右旋圆极化(RHCP)L波段B1、B2、B3频点发送服务信号。L波段伪距观测模型[7]如下：

(5)

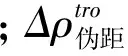
多路径误差采用双频伪距和载波相位组合观测值提取[8],长春站设置的GNSS接收机天线型号为NOV750.R4,可以有效抑制多路径效应,所以本文暂不考虑多路径效应的修正。电离层延迟通过对IGS提供的电离层产品内插来计算[9],这种方法的改正效果可以达到80%到90%,残差精度在2 ns左右。对流层延迟改正则采用Saastamoinen模型[10-12],改正精度最大不超过10 cm。卫星天线位置相对质心的坐标为(600.0,0.0,1100.0) mm,天线相位中心偏差改正为0.4 m。没有完善的修正模型,暂时不作考虑。

2.3 时间转换及时刻同步

在观测资料中,SLR采用协调世界时(UTC),UTC的秒长严格等于原子时长,有闰秒现象,BDS的时间基准是北斗时(BDT)。BDT是原子时,采用国际单位制(SI)秒为基本单位连续累计,不闰秒,在任何时候都与TAI(在整数秒上)相差33 s。BDT与UTC之间的整数秒差值的关系为：BDT≈DTAI+UTC-33 s。其中：DTAI=TAI-UTC。到目前为止,DTAI=35 s。本文根据此公式对BDT和UTC进行时间系统的换算。

SLR观测值记录时刻为激光信号发射时刻,BDS测距值记录时刻为微波信号到达接收机的时刻,由于两者记录时刻不同,所以需要进行时间基准的统一,本文采用拉格朗日八阶插值算法,以SLR观测时间为标准,对BDS测距值进行插值。

2.4 测站归心改正

实际观测中的SLR测距仪与GNSS接收机并不在同一位置,两种观测值不能直接比较,需要进行归心改正。改正公式[3]为：

(6)

3 计算与分析

3.1 数据来源

求解卫星钟差的数据采用2014年8月及9月长春站的SLR观测值和北斗L波段伪距观测值。考虑到BDS的星上设备时延差为基于B3频点的通道延迟偏差,单频的硬件延迟计算精度优于双频无电离层组合观测值[13],因此选用B3频点的伪距观测数据。长春站内建有SLR站,并设有GNSS接收机,两者相距不到百米,经站点归心改正后,可视为同一地址,其站址坐标如表1所示。本文使用的SLR观测值数据格式为full-rate,full-rate数据是SLR完整原始观测数据,包含了气象信息、测站延迟等信息。北斗伪距观测值来自GNSS接收机生成的RINEX格式文件。SLR测距系统和GNSS接收机时频信号来自同一原子钟。GFZ分析中心发布的钟差产品精度在0.2～0.8 ns,轨道产品精度为4～8 cm[14],此产品是基于B1频点和B2频点的无电离组合观测值得到的,本文利用DCB文件将此钟差产品转换为B3频点对应的精密钟差。为了验证本文解算出的导航卫星钟差的精度,使用GFZ发布的精密钟差数据与文中方法计算出的卫星钟差作外符比对。卫星钟差解算过程中用到的精密卫星星历和接收机钟差均来自GFZ发布的数据。

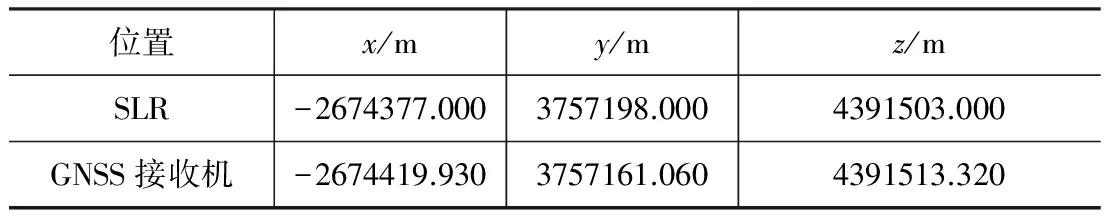
表1 长春人造卫星观测值并址站坐标

3.2 数据计算及分析

根据2014年8月中旬到9月中旬COMPASS-G1的SLR和北斗伪距观测数据的实际观测情况,本文处理了两者存在共同观测时段的8天数据。根据式(3)解算出卫星钟差,与内插得到的GFZ精密卫星钟差直接比较。表2给出了这8天计算的卫星钟差与GFZ精密卫星钟差算出的残差比较结果,图1为2014年8月28日使用本文方法计算出的COMPASS-G1卫星钟差和从GFZ精密卫星钟差插值得到的卫星钟差效果图。

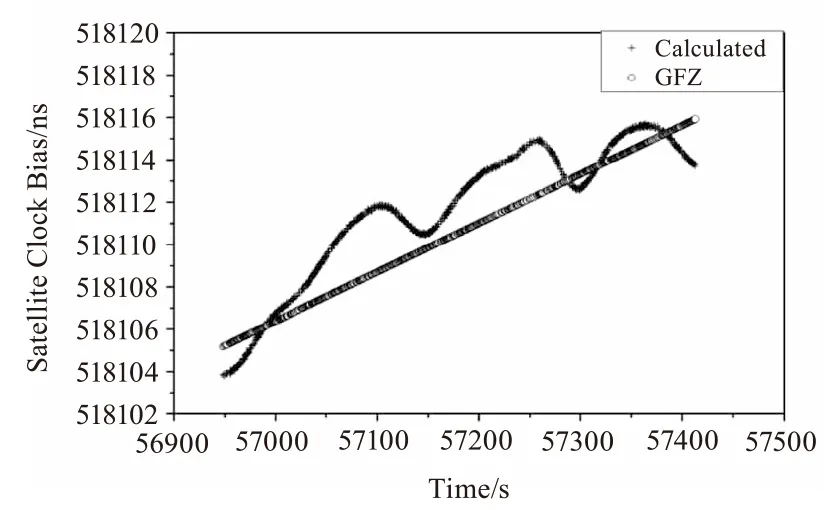
图1 本文解算的COMPASS-G1卫星钟差和GFZ卫星钟差

图2为根据这8天每天观测数据对应的相对观测时间绘制的残差效果图,即横轴为这8天的年积日,对应的观测时段范围见表2,其中253a表示9月10日上午观测值,253p表示9月10日下午观测值。

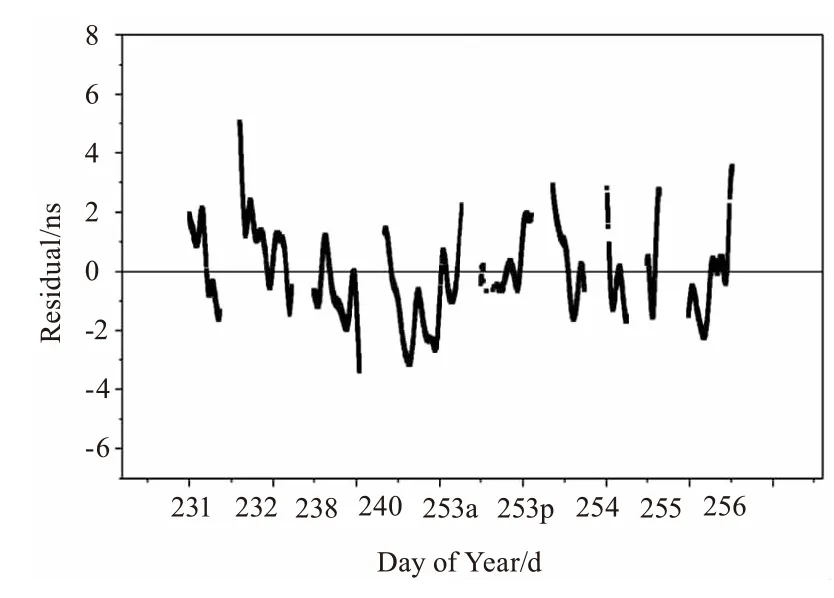
图2 长春站COMPASS-G1卫星钟差残差图

观测日期年积日时间最大值/ns最小值/ns平均值/ns中误差/ns2014-8-1923116：40-17：052．14-1．610．441．022014-8-2023212：30-12：405．04-1．461．050．842014-8-2623820：06-20：261．23-3．61-0．730．712014-8-2824015：50-16：072．22-3．17-0．991．042014-9-1025311：30-11：350．51-0．650．510．842014-9-1025311：40-12：054．01-1．620．210．962014-9-1125421：10-22：004．73-1．70-0．640．602014-9-1225510：30-10：402．77-1．560．161．352014-9-1325614：00-14：203．546-1．690．330．61

从表2中可以看到,8月19日、8月28日和9月12日这三天解算的COMPASS-G1卫星钟差残差的中误差比较大,这是因为这三天的观测时间长较短,数据相对较少的缘故。其他数据没有明显的系统差。由于该计算结果是采用单频伪距测量值解算的,且里面含有GFZ钟差产品的卫星钟差误差和接收机钟差误差,因此认为SLR和BDS单频伪距观测数据解算的卫星钟差精度在6 ns之内。

图1中使用本文方法计算得出的卫星钟差和GFZ卫星钟差产品插值得到的曲线相比,具有明显的波动,从图2也可以看出,这8天的数据都呈现波动性,这是主要是由接收机钟差变化引起的。图2中,将8天的计算数据放在一起观察,可见利用SLR和北斗伪距观测值计算的COMPASS-G1卫星钟差和GFZ精密卫星钟差从残差值在0上下浮动,说明在两者的变化趋势是一致的。

4 结 论

本文阐述了利用SLR观测值和北斗L波段单频伪距观测值进行BDS卫星钟差求解的方法,实验结果表明用该方法来解算COMPASS-G1高轨道卫星卫星钟差是可行的。该方法实现了利用单站单频观测值解算BDS卫星钟差,减弱了组差求卫星钟差时测站坐标与钟差的相互影响。由于受BDS伪距观测值的精度所限,利用文中计算方法求得卫星钟差精度在6ns之内。

[1] Catal N C,Hern Ndez C,Mozo A,et al.Improved integrity concept for future GNSS evolutions//[C].Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation,2008,2547-2557.

[2] QIN Xianping,YANG Yuanxi,JIAO Wenhai,et al.Determination of navigation satellite clock bias using SLR and pseudorange data[J].Acta Geodaetica Et Cartographic Sinica,2004,33:205-209.(in Chinese)

秦显平,杨元喜,焦文海,等.利用SLR和伪距资料确定导航卫星钟差[J].测绘学报,2004,33(3):205-209.

[3] MAO Yue,JIA Xiaolin,QIN Xianping.Validating clock bias of satellite using SLR and pseudorange data[J].Geomatics and Information Science of Wuhan University.2007,32(12)：1160-1163.(in Chinese)

毛悦,贾小林,秦显平.利用SLR及伪距数据进行卫星预报钟差精度验证[J].武汉大学学报· 信息科学版,2007,32(12)：1160-1163.

[4] HUANG Baoli,HAN Xingwei,ZHANG Nan,et al.Axis correction of satellite laser ranging system based on image processing technique[J].Laser & Infrared,2014,44(7):715-719.(in Chinese)

黄宝利,韩兴伟,张楠，等.卫星激光测距系统的指向偏差修正[J].激光与红外,2014,44(7):715-719.

[5] LI Ji-sheng.Satellite precision orbit determination[M].Beijing:The People’s Liberation Army Press,1995.(in Chinese)

李济生.人造卫星精密轨道确定[ M].北京:解放军出版社,1995.

[6] MARINI J W.Correction of satellite tracking data for an arbitrary tropospheric profile[J].Radio Science,1972,7(2):223-31.

[7] LI Zheng-hang ,HUANG Jin-song,et al.GPS Surveying and data processing[M].Wuhan:Wuhan University Press,2010.(in Chinese)

李征航,黄劲松,等.GPS 测量与数据处理[M].武汉:武汉大学出版社,2010.

[8] 陆亚峰,楼立志,马绪瀛,等.北斗伪距多路径分析及单点定位解算[J].矿山测量,2013 (4):18-21.

[9] WANG Wukui,LIU Changjian,WU Hongju.Interpolating algorithm analysis of IGS Ionosphere VTEC Product[J].Gnss World of China,2013,38(6):17-21.(in Chinese)

王五魁,刘长建,吴洪举.IGS电离层VTEC产品内插算法解析[J].全球定位系统,2013,38(6):17-21.

[10]Saastamoinen J.Contributions to the theory of atmospheric refraction[J].Bulletin Géodésique (1946-1975),1973,107(1):13-34.

[11]Saastamoinen J.Contributions to the theory of atmospheric refraction[J].Bulletin Geodesique,1972,105(1):279-298.

[12]Saastamoinen J.Introduction to practical computation of astronomical refraction[J].Bulletin Géodésique (1946-1975),1972,106(1):383-97.

[13]Huang S,Wang X,Liu L,et al.Separation solution methods of TGD and IFB for compass system[J].Geomatic Science and Engineering,2010,3:28-32.

[14]MacLeod K,Caissy M.Real time IGS pilot project (RT-PP) status report[C].IGS Workshop,New-castle UK,2010.

Calculation of COMPASS satellite clock bias using SLR and L-band simultaneous observation data

HU Jia-yu1,2,HAN Xing-wei1,ZHANG Zi-ang1

(1.Changchun Observatory/NAO,Chinese Academy of Sciences,Changchun 130117,China；2.University of Chinese Academy of Sciences,Beijing 100049,China)

The clock bias of navigation satellite is usually millisecond level,and the positioning accuracy of navigation will be affected obviously if the clock bias is not precisely corrected.The principle and calculating method of the BDS satellite clock bias based on SLR and L-band pseudo-range co-location data were described.The clock bias of COMPASS-G1 was computed using the observation data of September 2014 provided by Changchun Observatory.The clock bias is compared with the reference clock bias offered from GFZ.Comparison and analysis results show that the difference of two COMPASS-G1 clock biases is less than 6 ns.It shows that this calculating method of BDS satellite clock bias in this paper is feasible.

satellite laser ranging(SLR);BeiDou Navigation Satellite system(BDS(COMPASS));L-band observation data;satellite clock bias

1001-5078(2015)11-1314-05

中国科学院精密导航定位与定时技术重点实验室开放基金(No.2014PNTT10);国家自然科学基金(No.11103047，11373047)资助。

胡佳钰(1988-),女，在读研究生，学士，专业为天体测量与天体力学。E-mail：hujy@cho.ac.cn

2015-03-19;

2015-04-08

TN249

A

10.3969/j.issn.1001-5078.2015.11.006