大气湍流对高斯光束瑞利区间的影响

王 慧,杨 军,章 曦

(解放军理工大学理学院,江苏 南京 211101)



·光学技术·

大气湍流对高斯光束瑞利区间的影响

王 慧,杨 军,章 曦

(解放军理工大学理学院,江苏 南京 211101)

瑞利区间;高斯光束;大气湍流;Andrews修正谱;Von Karman谱

1 引 言

激光束在大气中传输时由于受到大气湍流的影响,易发生光强闪烁、波前失真以及光束快速扩展等现象,从而限制了激光的实际应用。大气湍流还可以使得激光光束的相干性发生退化[1]。1990年,Wu[2]从理论上证明了部分空间相干光受大气湍流的影响比完全相干光受到的影响小。2002年,Gbur等[3]给出了部分空间相干光受大气湍流影响的条件,并得到了Dogariu等[4]的实验验证。考虑到大气湍流的随机性,可以运用大气折射率起伏功率谱密度模型来描述大气湍流的特征,本文主要采用L.C.Andrews修正谱(M谱),并将计算结果与Von Karman谱的计算结果进行对照。在激光理论中,瑞利区间表示完全相干激光光束无明显扩展的传输距离,后来Gbur等[3]把这一概念拓展到部分相干光,最近激光束瑞利区间的概念进一步从自由空间拓展到大气湍流中,大气湍流使得激光光束瑞利区间缩短,湍流越强瑞利区间越短[5]。本文根据部分相干双曲余弦高斯光束在自由空间和湍流大气中传输光束瑞利区间的解析结果,采用M谱进行数值分析,研究了大气湍流的尺寸效应、相干参数、光束参数、大气湍流内尺度、束腰宽度和折射率起伏结构常数等对部分相干双曲余弦高斯光束在自由空间和实际空间中传输的影响,并将结果与其他相关研究工作进行对比[6-7],为实际应用提供参考。

2 理论模型

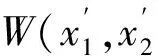
其中:

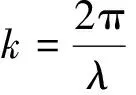
在自由空间中,瑞利区间ZRfree定义为光束横截面积扩展到源场处面积的两倍时光束所传输的距离。因此部分相干双曲余弦高斯光束通过自由空间传输的瑞利区间为:

(1)

根据文献[11-12]可知,在大气湍流中部分相干光的二阶矩x2可写为:

(2)

3 数值计算结果与分析

大气折射率起伏功率谱模型的选取非常重要[13],本文主要采用适用于各种强度湍流大气的M谱,即:

(3)

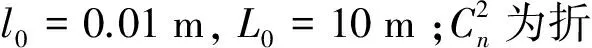
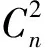
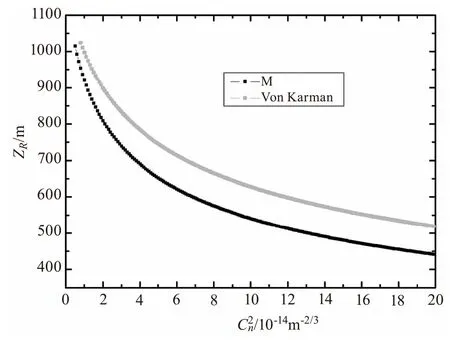
图1 ZR随变化关系图(ω0=0.02m,α=1,β=1,λ=1.06 μm)

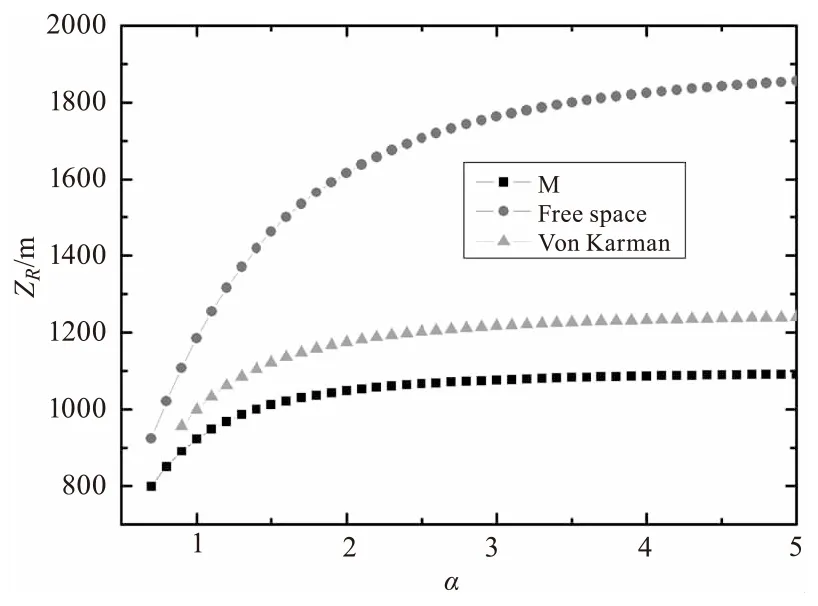
图2 ZR随α变化关系图(ω0=0.02 m,β=1,

图2 给出了Von Karman谱和M谱的瑞利区间ZR随光束相干参数α变化关系曲线,作为对比同时给出了自由空间的瑞利区间。从图2中可以看出,相比于自由空间,大气湍流的存在大幅度降低了激光传输的瑞利区间,瑞利区间ZR随相干参数α的增加而增加,但当α>2时,曲线斜率明显减小,说明继续增加光束的相干性对提高瑞利区间ZR影响较小。同样,Von Karman谱和M谱对瑞利区间随光束相干参数α变化的影响趋势相同,但是M谱计算得出的瑞利区间比相同条件下Von Karman谱计算得出的瑞利区间稍小。

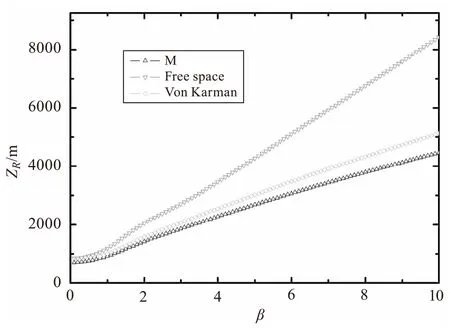
图3 ZR随β变化图(ω0=0.02 m,α=1,

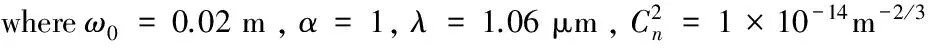
图3 是Von Karman谱和M谱的瑞利区间ZR随光束参数β变化曲线,从图中可以看出,瑞利区间ZR随光束参数β的增加而增加,特别当β>2则近似于线性增加,说明激光传输过程中的光束参数和束腰宽度都对瑞利区间的变化影响显著,在实际应用中,应该尽可能提高光束参数的大小以利于瑞利区间的增加,提高通信质量。

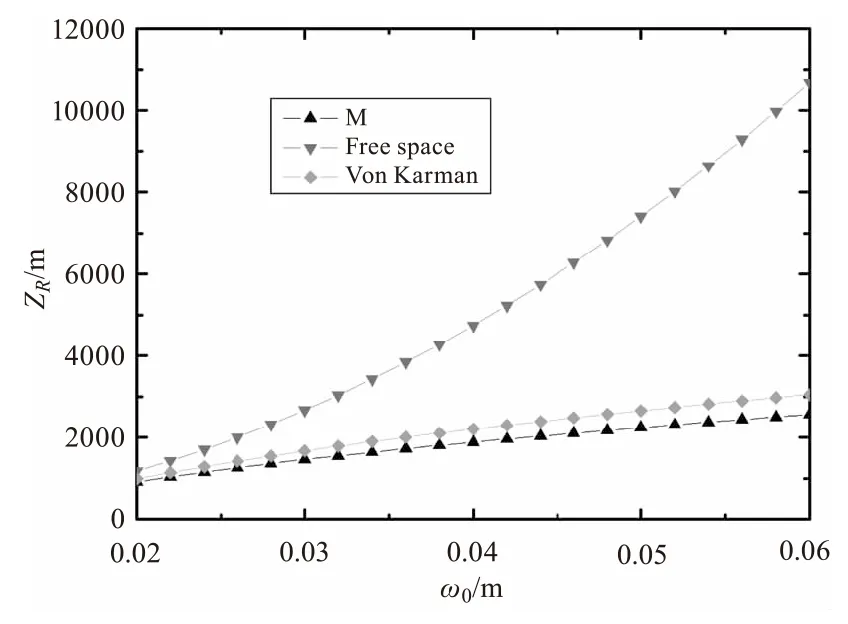
图4 ZR随ω0变化关系图(α=1,β=1,

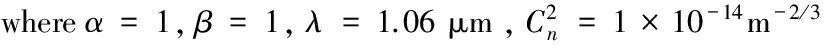
图4 给出的是Von Karman谱和M谱的瑞利区间ZR随束腰宽度w0变化曲线,图中可以看出,在自由空间中,瑞利区间随高斯束宽的增加而显著增大,但在实际空间中,瑞利区间仍然呈现出增加的趋势,但增加趋势明显降低,所以增加束腰宽度对激光的相位保持是有利的。

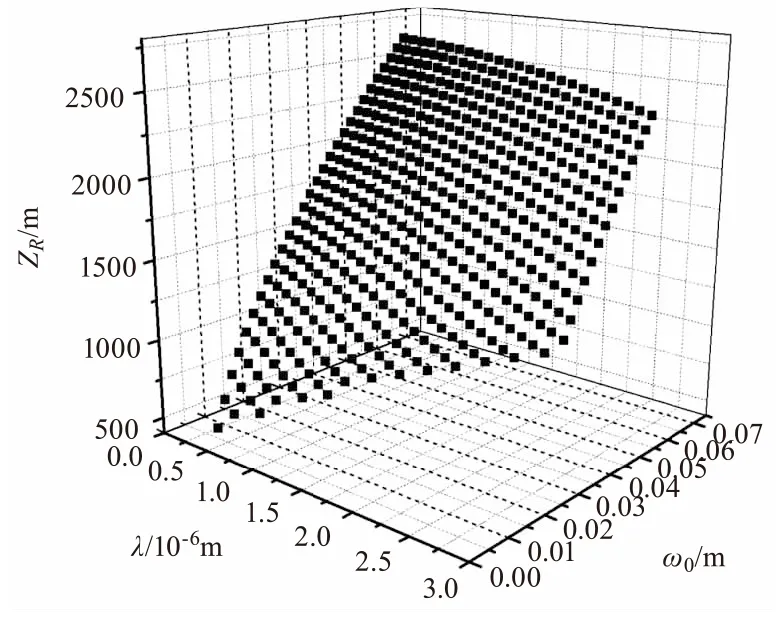
图5 ZR随λ与ω0变化关系图

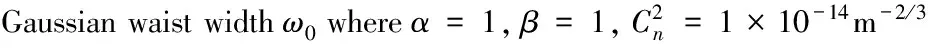
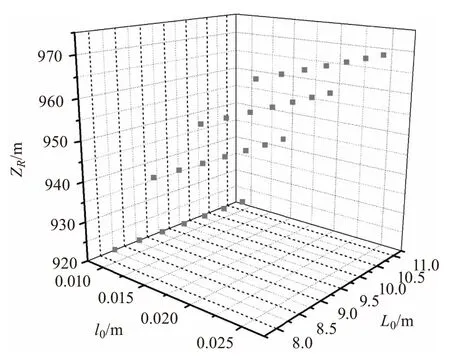
图6 ZR随L0与l0变化关系图(α=1,β=1,

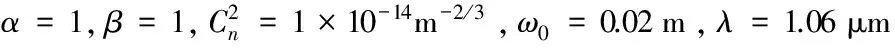
图5和图6给出了瑞利区间随湍流尺寸及激光波长的对应关系。图5表明波长λ越小、束腰宽度ω0越大,瑞利区间ZR越大。光束波长越小,则光子的能量越大,其受散射作用相对越弱,因此瑞利区间越大。因此实际应用中可以通过提高相干参数α、提高光束参数β、增加束腰宽度ω0以及减小光束波长λ来提高瑞利区间ZR。图6表明瑞利区间ZR受湍流外尺度L0变化的影响较小,而受湍流内尺度l0变化的影响较大,湍流内尺度l0越大,瑞利区间ZR越大,表现出明显的尺寸效应。大气湍流内尺度在地面附近的典型测量结果是几个毫米,并且随高度的增加而增加,最大能够达到几十厘米,因此选择湍流内尺度较大的区域有利于提高瑞利区间。

4 结 论

[1] Ji X L,Eyyuboglu H T,Baykal Y.Influence of turbulence on the effective radius of curvature of radial Gaussian array beams[J].Opt.Express,2010,18(7):6922-6928.

[2] Wu J.Propagation of a Gaussian-Schell beam through turbulent media[J].J.Mod.Opt,1990,37:671-684.

[3] Gbur G,Wolf E.Spreading of partially coherent beams in random media[J].J.Opt.Soc.Am.A,2002,19:1592-1598.

[4] Dogariu A,Amarande S.Propagation of partially coherent beams:turbulence-induced degradation[J].Opt.Lett,2003,28:10-12.

[5] JI Xiaoling.Influence of the atmosphericc turbulence on propagation properties of laser beams[J].Journal of Sichuan Normal University:Nature Science,2012,35:127-136.(in Chinese)

季小玲.大气湍流对激光束传输特性的影响[J].四川师范大学学报:自然科学版,2012,35:127-136.

[6] JI Xiaoling.Influence of turbulence on the Payleigh range of partially coherent cosh-Gaussian beams[J].Acta Phys.Sin.,2011,60:064207.(in Chinese)

季小玲.湍流对部分相干双曲余弦高斯光束的瑞利区间的影响[J].物理学报,2011,60:064207.

[7] LI Jinhong,LÜ Baida.Comparative study of partially coherent vortex beam propagations through atmospheric turbulence along an uplink path and a downlink path[J].Acta Phys.Sin.,2011,60:074205.(in Chinese)

李晋红,吕百达.部分相干涡旋光束通过大气湍流上行和下行传输的比较研究[J].物理学报,2011,60:074205.

[8] Casperson L W,Tovar A A.Hermite-sinusoidal-Gaussian beams in complex optical systems[J].J.Opt.Soc.Am.A,1998,15(4):954-961.

[9] Zahid M,Zubairy M S.Directionality of partially coherent Bessel-Gauss beams[J].Opt Comm,1989,70(5):361-364.

[10]Siegman A E.New developments in laser resonators[C].SPIE,1990,1224:2-14.

[11]Dan Y,Zhang B.Second moments of partially coherent beams in atmospheric turbulence[J].Opt.Lett,2009,34(5):563-565.

[12]Ji X L,Li X Q.Effective radius of curvature of partially coherent Hermite-Gaussian beams propagation through atmospheric turbulence[J].Opt.,2010,12(3):035403.

[13]LIU Yangyang,LÜ Qiunbo,ZHANG Wenxi.Simulation for space target interference imaging system distorted by atmospheric turbulence.Acta Phys.Sin.,2012,61(12):124201.(in Chinese)

刘扬阳,吕群波,张文喜.大气湍流畸变对空间目标清晰干涉成像仿真研究[J].物理学报,2012,61(12):124201.

[14]Salem M,Korotkova O,Dogariu A,et al.Polarization changes in partially coherent electromagnetic beams propagating through the turbulent atmosphere[J].Waves in Random Media,2004,14(4):513-523.

[15]Zhang E T,Ji X L,Lv B D.Propagation of the off-axis superposition of partially coherent beams through atmospheric turbulence[J].Chin.Phys.B,2009,18(2):571-580.

[16]Casperson W L,Hall D G.Sinusoidal-Gaussian beams in complex optical system[J].J.Opt.Soc.Am.A.,1997,14(12):3341-3348.

[17]YUAN Zhongheng,ZHANG Wentao.The analisis and research for the laser beam through onflow atmosphere channel[J].Laser & Infrared,2006,36(4):272-274.(in Chinese)

袁纵横,张文涛.大气湍流对激光信号传输影响的分析研究[J].激光与红外,2006,36(4):272-274.

[18]XIANG Libin,YUAN Yan,LÜ Qunbo.Spectral transfer function of the fourier transform spectral imager[J].Acta Phys.Sin.，2009,58(8):5400.(in Chinese)

相里斌,袁艳,吕群波.傅里叶变换光谱成像仪光谱传递函数研究[J].物理学报,2009,58(8):5400.

[19]WU Lin,YING Jiaju,GENG Biao.Effect on laser propagation in the atmosphere turbulence[J].Laser & Infrared,2008,38(10):974-977.(in Chinese)

武琳,应家驹,耿彪.大气湍流对激光传输的影响[J].激光与红外,2008,38(10):974-977.

[20]ZHU Lin,SONG Miao.Numerical simulation of the impact of atmospheric turbulence on the laser signal[J].Laser & Infrared,2013,43(11):1268-1272.(in Chinese)

朱耀麟,宋苗.大气湍流对激光信号影响的数值模拟[J].激光与红外,2013,43(11):1268-1272.

Influence of atmospheric turbulence on the Rayleigh range of Gaussian beams

WANG Hui,YANG Jun,ZHANG Xi

(Institute of Science,PLA University of Science and Technology,Nanjing 211101,China)

Rayleigh range;Gaussian beam;atmospheric turbulence;Andrews modified fluctuation spectrum;Von Karman fluctuation spectrum

1001-5078(2015)11-1355-05

总参谋部信息化部通信指挥装备军内科研基金(No.KYLYZXJK140002)资助。

王 慧(1981-),男,讲师,主研领域为激光传输理论。E-mail：wanghuinj@foxmail.com

2015-03-23;

2015-04-09

O436

A

10.3969/j.issn.1001-5078.2015.11.014