结合蚁群算法与二维直方图的红外图像分割
2015-11-24温凯峰
温凯峰
(嘉应学院,广东 梅州 514015)
·图像与信号处理·
结合蚁群算法与二维直方图的红外图像分割
温凯峰
(嘉应学院,广东 梅州 514015)
现有的图像分割算法存在着耗时量大,分割效果不佳等问题,不适用与红外系统领域的应用。针对上述问题,根据灰度级-梯度二维直方图的目标分割优势,通过与蚁群算法相结合,提出了一种结合蚁群算法与二维直方图的红外图像分割算法。通过在传统的灰度-梯度二维直方图进行引入边缘与噪声区域的相关量;通过将图像窗口化,并根据最佳分割阈值对蚁群的启发函数以及信息素更新进行重新定义,来实现红外目标的快速提取。实验结果表明,该算法分割后的红外目标边缘清晰,抗干扰能力较强,且运算速度也得到了有效提高。
分割算法;二维直方图;蚁群算法;红外图像;阈值
1 引 言
图像分割是通过将图像分割成具有不同特性的区域,使各区间的表现出一致性或相似性的图像处理算法;如今在图像分析、图像识别以及图像检测等领域占据着重要的地位,也是目前的研究热点之一。为了有效地对目标信号进行分割,人们深入地对其进行研究,提出了不少图像分割算法,如阈值分割法[1-2]、模糊聚类分割法[3-5]以及直方图割法[6-7]等,并且在这些算法的基础上,人们通过大量的研究也提出了许多改进的算法,使图像分割得到了较大的发展[8-10]。而在红外成像系统中,由于检测运动目标时,当探测器距离目标较远且在图像上只占很小的面积时,会使得现有的目标分割算法难以实现对红外图像目标的准确分割。
为了解决上述问题,提出了一种针对红外成像系统的红外目标分割算法,通过对比分析传统二维直方图分割算法的原理及分割效果[11],然后选用灰度级-梯度二维直方图并对其进行适当的改进;并根据蚁群算法具有的离散性与鲁棒性特点[12],通过对窗口的改进,以及信息素,路径选择等进行改进,使其更好地与灰度级-梯度二维直方图分割算法进行结合,来实现对红外图像进行准确分割。最后与其他经典的分割算法进行分割效果以及耗时等方面的对比,实验结果表明,该算法能够在不同条件下实现对红外目标的提取,具有准确性高,耗时少的分割优势。
2 二维直方图
传统的二维直方图可以大致分为两种,即灰度级-平均灰度级二维直方图与灰度级-梯度二维直方图。下面对上述两种二维直方图进行对比。
设图像的大小为N×M,灰度级取0,1,…,L-1;选用baboon分别采用上述两种二维直方图进行处理,图1为灰度级-平均灰度二维直方图,图2为灰度级-梯度二维直方图。其中结合图像的ioj平面图与目标与背景分割图来对这两种二维直方图进行分析。
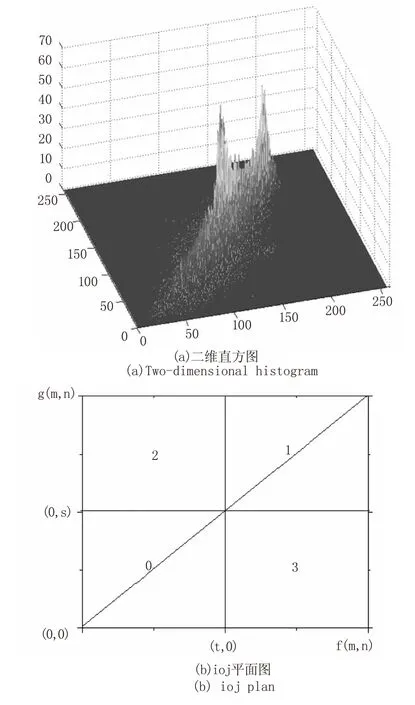
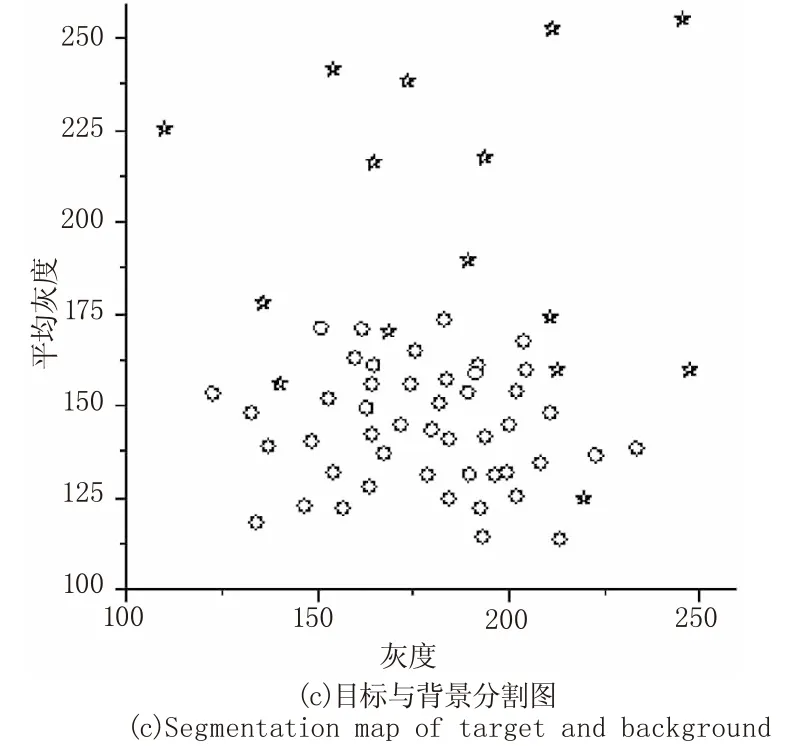
图1 灰度级-平均灰度二维直方图Fig.1 two-dimensional histogram of gray level-the average gray
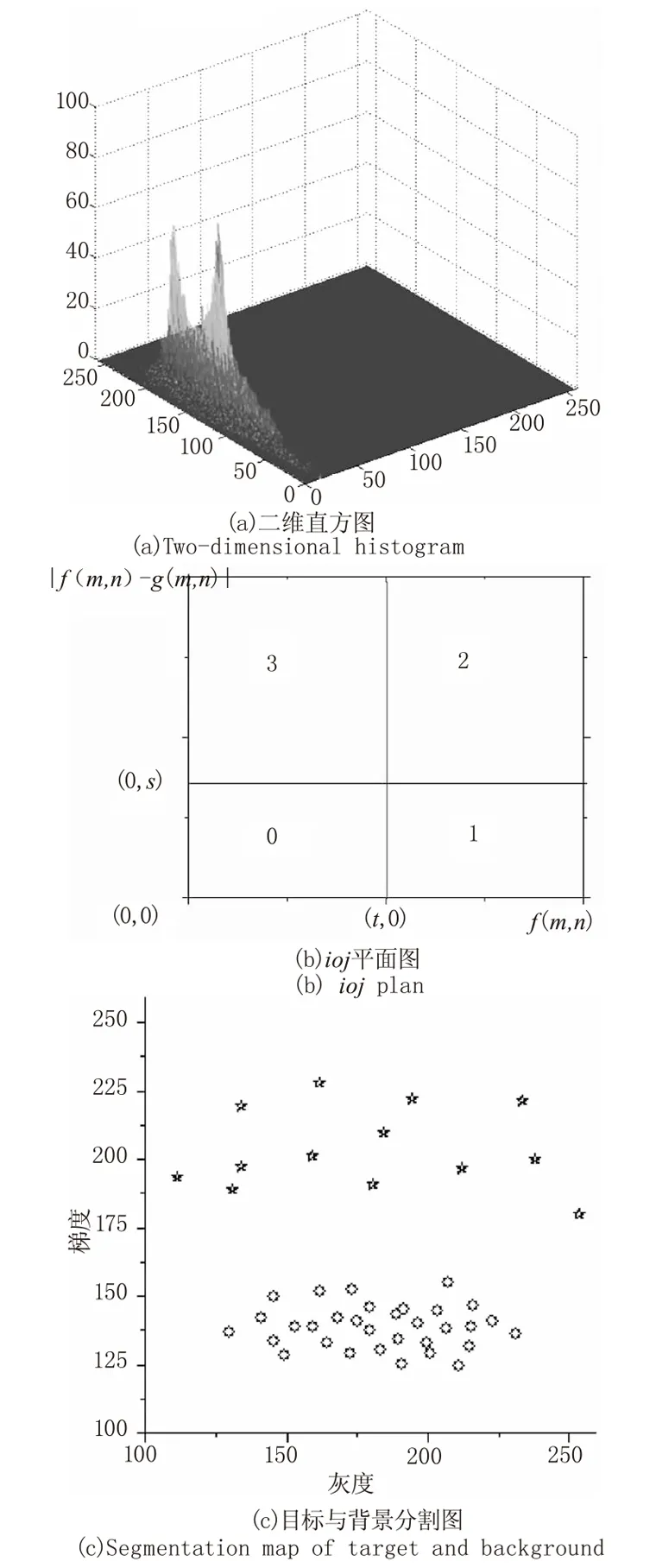
图2 灰度级-梯度二维直方图Fig.2 Two-dimensional histogram of gray level-gradient
其中灰度级-平均灰度二维直方图认为区域0与1分别代表目标与背景,而区域2和3则代表边缘和噪声;通过观察图1(c)可以看到,该算法通过择优算法来减少计算量,但在计算的过程中往往会将目标内点与背景内点误判为边缘和噪声,使计算最佳阈值出现偏差。与之相比,灰度级-梯度二维直方图通过结合图像分灰度梯度关系,有效地将图像的目标与背景中的边缘信号与噪声信号进行分离,最终得到图2(c)的分割效果。
而针对红外图像的特性,由于背景的纹理比较少,使得目标边缘与背景容易混合在一起,从而在图像分割的过程中,将目标信号中的部分有效信号分割掉,不利于图像分割质量的保护。因此,本文选用灰度级-梯度二维直方图并对其进行改进。
3 本文算法
3.1 定义最佳分割阈值
通过观察图3二维直方图的ioj平面图可以清楚地看到,在平面图中除了目标区域与背景区域还有边缘信息与噪声信号,而其中比例占得最大的为图像边缘信息,而传统的最佳分割阈值中,只考虑图像的目标信号与背景信号,而忽略了边缘信号与噪声信息,这很大程度地将图像中很大的一部分有效信号被强制性的删去,使得图像在分割的过程中,降低了分割图像的质量[13]。
为了避免该现象的发生,分别对图像的边缘与噪声信号进行定义,并将其融入最佳分割阈值中,来提高算法的分割效果;其方法如下所示,其中图3为灰度级-梯度二维直方图ioj平面图。

图3 灰度级-梯度二维直方图ioj平面图Fig.3 Two-dimensional histogram ioj plan of gray level-gradient
设边缘区域与噪声区域的概率函数分别为:
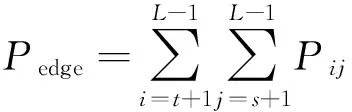
并对其各个区域的概率进行归一化处理,使得每个区域中的概率和为1,同时有利于算法的简化;其归一化处理后的各区域间的概率函数分别如下所示:
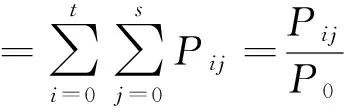
(1)
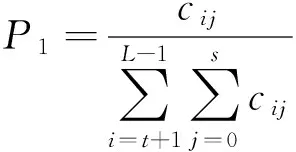
则各区域的二维相关量函数表达式如下:
目标二维相关量:
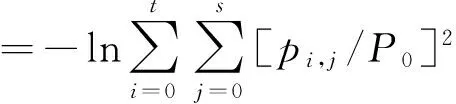
背景二维相关量:
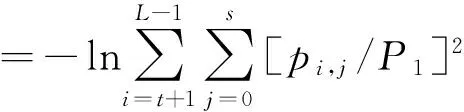
边缘二维相关量:

噪声二维相关量:

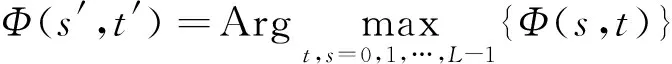
(2)
3.2 基于蚁群算法的图像分割算法
3.2.1 搜索窗口的优化
在采用蚁群算法进行红外图像分割的时候,会先对图像的每个像素点放置一只蚂蚁,假设原始的图像大小为N×M,且灰度级为L=256,则蚂蚁在多次循环搜索的过程中,每一只蚂蚁与其余的N×M-1在都比较进行多次距离与路径转移的概率计算,这使得搜索的时间以及所需的计算量相当的大[14]。
而在图像进行灰度级-梯度二维直方图相关量计算时,可以快速有效地计算出图像各类信号间的关系,针对这一特性,本文先将原始红外图像划分为多个小窗口,通过以一个窗口为单位进行计算,对其进行蚁群算法处理,从而提高算法的分割算法。其方法如下:
(1)窗口的划分
其中窗口的大小会间接地影响到图像分割质量;即当窗口过大时,虽能很大程度地减少分割的计算量,但却容易陷入局部的最优现象;当窗口过小时,虽能减少小窗口内蚂蚁的路径转移次数,但却又会使计算量变大,从而不利于红外图像的快速分割。
为了保证各分割块间的计算出来的窗口间相关值差异过大而陷入局部最优的现象,以及根据目标图像表述特性,本文将各窗口限制为正方形。
设原始的红外图像I有pij=nij/(N×M),nij=1/dij,其中dij为蚂蚁从i到j之间的距离。通过对源图像进行灰度级-梯度二维直方图处理,可以得到概率均等的分块,即分为N×M块;而为了限制其图像的大小,本文进行以下定义。
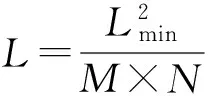
(2)窗口的信息素的行定义
在传统的窗口信息素算法中,都是对划分出来的小窗口进行整块的计算,最终求取其均值来表示该块的信息素浓度;但通过研究发现,在红外图像中,根据其图像空间的相关性,在划分出来的二维直
方图小窗口中,其当前块的左邻块、上邻块以及右上邻块的信息素为当前块信息的主要信息块,通过对其计算能够有效地计算出当前块的信息素大小,进而减少了对分割块的计算量,图4为当前块的相邻块。

图4 当前块的相邻块Fig.4 Neighboring blocks of the current block
但为了提高各块间信息素的适应度,其中信息素的浓度反映的是图像目标信号的相关程度大小,其中信息素越大,目标越接近,反之为背景信号。
即当前块中信息素的浓度系数为:
其中,Max(Pij)、Min(Pij)表示的当前块中被选上的最大概率与最小概率。为了防止部分信息素由于循环次数的增加,而使其窗口中信息素含量趋向于零,或由于信息素浓度过高,而出现局部最优化现象,本文对各窗口中的信息浓度进行限制,其方法如下。
在每个窗口中,将信息素浓度的值域限制在[ωmin(i,j),ωmax(i,j)]区间内,通过根据这一限制条件,使得每次循环后,各小窗口的信息素浓度ωmin(i,j)≤ω(i,j)≤ωmax(i,j),则窗口的信息素:
(3)
3.2.2 启发函数的设置
将二维最大分割阈值与启发函数进行结合,得到新的启发函数为:
η(i1,j1)(i2,j2)=Φ(s′,t′)(i2,j2)-
Φ(s′,t′)(i1,j1)
其中,η(i1,j1)(i2,j2)表示的是当前蚂蚁K由块(i1,j1)转移到块(i2,j2)的期望值。
当η(i1,j1)(i2,j2)≥0时,蚂蚁以p(i1,j1)(i2,j2)的概率进行转移到目标块(i2,j2);
当η(i1,j1)(i2,j2)<0时,蚂蚁在原地停留,即依然在块(i1,j1)。
其中,蚂蚁转移的概率为:
其中,α为信息启发式因子,主要反映的是累积信息在蚂蚁运动时所起的作用;β为期望启发式因子,主要反映的是启发信息在选择路径时受重视的程度;这两个参数的最佳组合一般由经验来确定。
为了实现蚁群对目标的快速搜索,在这里,本文对其路径的选择进行了定义;其中,在初始时刻,图像搜索的各路径上的信息素相同,都为ε(ε为常数),即γi,j(0)=ε;则蚂蚁k在路径选择的过程中,根据各窗口信息素浓度进行转移,即:
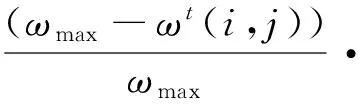
pk(i1,j1)(i2,j2)
(4)
3.2.3 信息素的更新
与传统的蚁群算法相同,在图像分割的过程中,随着时间的增长,其搜索路径中的信息素会逐渐的挥发,并根据每次搜索的完成,对全图的信息素进行更新,即:
γi,j(t,t+1)=φ·γi,j(t,t+1)+(1-φ)·
Δγi,j(t,t+1)
其中,φ为信息素的遗留程度;Δγi,j(t,t+1)为信息素更新函数,但是为了避免对时间序列过分分割,引入的最佳分割阈值,对其信息素的更新进行限制,即:
Δγi,j(t,t+1)=[Φ(t′,s′)-Φ(t,t+1)]·
(5)
当找到最佳阈值时,则停止对信息素的更新。
3.2.4 随机搜索蚂蚁
为了在全局搜索过程中,能够快速有效地对图像进行搜索,本文在其全局搜索的过程中,引入随机搜索蚂蚁,通过挑选一部分蚂蚁为随机搜索蚂蚁,在并根据循环次数的增加,算法的随机搜索蚂蚁也将逐渐地减少,直到得到算法的最佳分割阈值,则停止随机搜索蚂蚁的引入。其随机搜索函数为:
(6)
其中,Φ(t)为t时刻的二维阈值;Φ(s′,t′)为分割算法中的最佳分割阈值,而n表示的是迭代搜索次数。
3.3 本文算法流程
Step 1:算法的初始化,设置算法的相关初始化参数。
Step 2:根据公式(2)对算法的最佳分割阈值进行预定义。
Step 2:对原始的红外图像进行处理,求取其二维直方图,并定义图中每一个数据对应一只蚂蚁。
Step 3:通过将原始红外图像划分为多个小窗口,通过以一个窗口为单位进行计算,对其进行蚁群算法处理,并结合公式(3)对窗口中的信息素进行求取。
Step 4:根据公式(4)对各路径上的信息素浓度进行计算,并结合公式(5)进行信息素的更新。
Step 5:为了在全局搜索过程中,通过结合公式(6)引入随机搜索蚂蚁,来加快算法对图像的搜索。
Step 6:最终通过多次迭代的搜索确定图像的最佳分割阈值,则停止对信息素的更新。
4 仿真实验
为验证本文算法在红外图像分割的分割效果,本文对算法实验参数进行了设置以及测试环境进行了选取;其中本文算法的实验参数为:蚁群中蚂蚁的初始数量与图像的像素点数量相同,蚁群搜索的循环次数为200,迭代次数为5;而信息启发式因子α=3,期望启发式因子β=2;为了避免信息素过大与过小等现象的发生,本文对其信息素浓度进行限制,即信息素浓度最大值ωmax(i,j)=0.8,则最小为ωmin(i,j)=0.2。实验测试环境如表1所示。

表1 测试环境Tab.1 Test environment
本文选用多组红外图像对算法进行验证,并与传统的Ostu算法、灰度级-平均灰度级二维直方图分割算法、传统的灰度级-梯度二维直方图分割算法以及文献[15]算法进行对比,来实现各算法的分割效果的对比;图5为实验的原始红外图像。经实验,得到各算法的处理结果图,如图6所示。
通过对比各算法的处理结果图可以看到,本文算法在目标分割方面与文献[15]算法相差无几,但优于其他几种算法,其中Ostu算法虽然能够有效地将目标图像分割出来,但往往夹杂着许多无关信息,导致信息分割的不是很明确;灰度级-平均灰度级算法则是存在着不能将目标信号完成分割的问题,在分割的过程中,忽略了对边缘区域的保护,导致目标信号出现过多分割的现象;而灰度级-梯度算法虽然能够有效地提取图像内部与边缘信号,但得到的有效信息过多从而存在一些干扰。为了进一步进行比较,从均匀测度值与分割消耗时间进行比较,最终得到各算法均匀测度值与耗时数据对比表,如表2所示。
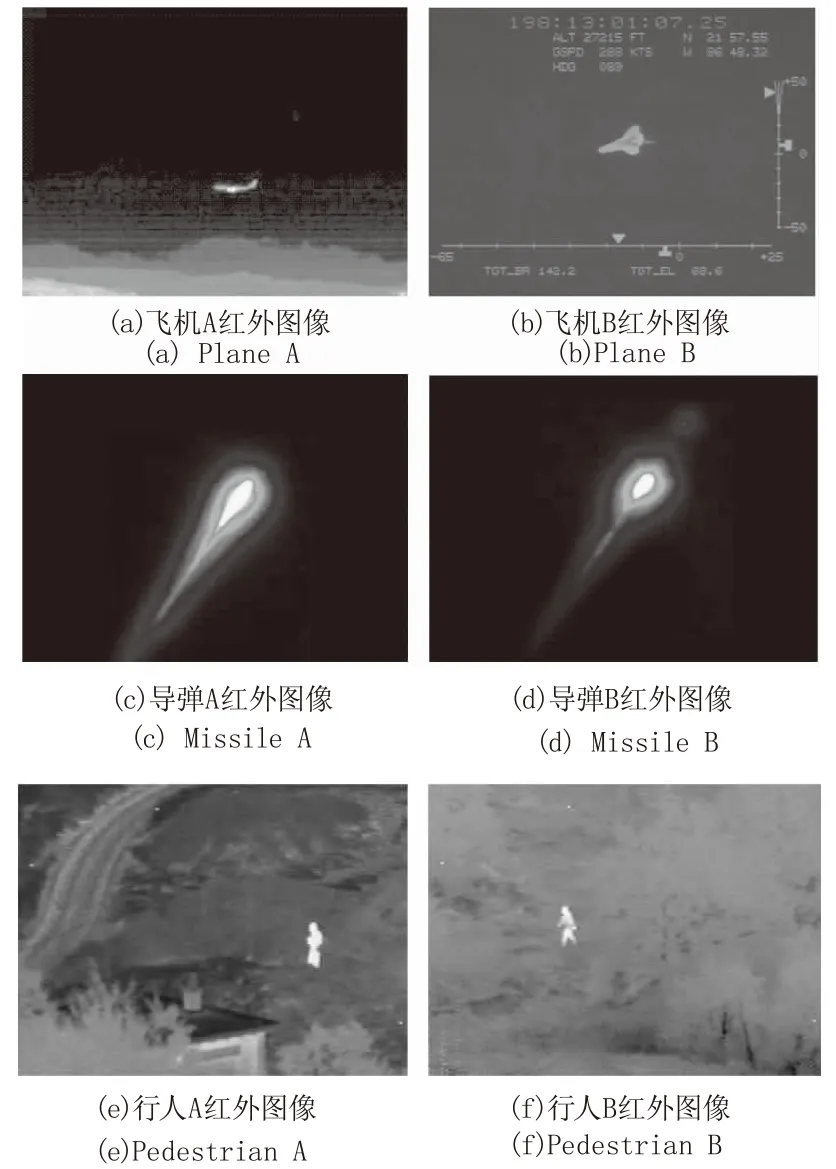
图5 仿真实验原图Fig.5 Original image of simulation

图6 各算法的处理结果图Fig.6 The results of each algorithms表2 各算法均匀测度值与耗时数据对比表Tab.2 Comparison of uniform measure and run time for different algorithms
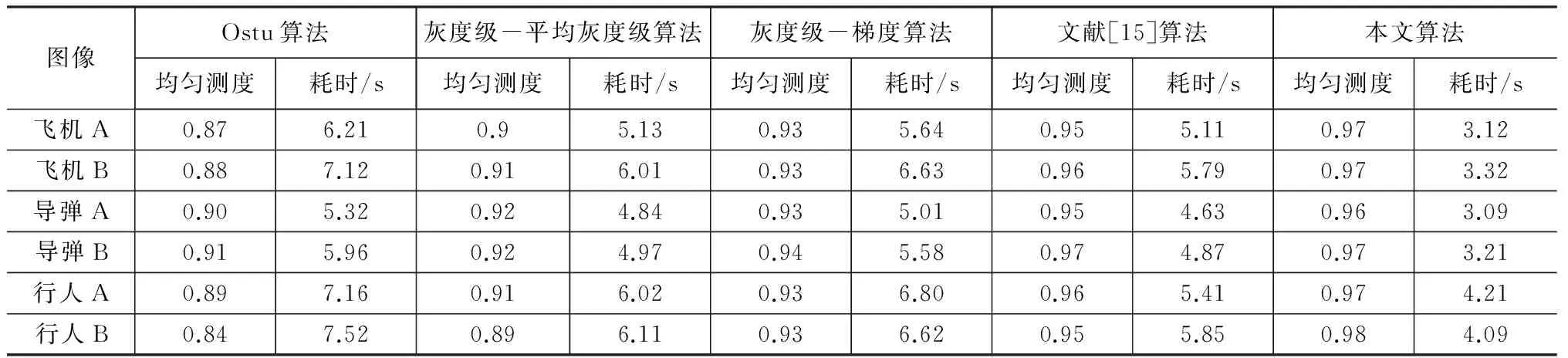
图像Ostu算法均匀测度耗时/s灰度级-平均灰度级算法均匀测度耗时/s灰度级-梯度算法均匀测度耗时/s文献[15]算法均匀测度耗时/s本文算法均匀测度耗时/s飞机A0.876.210.95.130.935.640.955.110.973.12飞机B0.887.120.916.010.936.630.965.790.973.32导弹A0.905.320.924.840.935.010.954.630.963.09导弹B0.915.960.924.970.945.580.974.870.973.21行人A0.897.160.916.020.936.800.965.410.974.21行人B0.847.520.896.110.936.620.955.850.984.09
通过观察表2可以看到,本文算法在均匀测度值与分割耗时方面都优于其他算法,其中均匀测度值代表的是图像分割效果的标准参数,当均匀测度值越大时,相应的算法分割效果越好;而通过对比可以看到,本文算法的均匀测度值比文献[15]算法的平均高出0.013;而在耗时方面,本文算法则比文献[15]算法平均节约了1.77 s;有效地证明了算法的可行性。
5 结束语
本文提出了一种结合蚁群算法与二维直方图的红外图像分割算法,该算法通过在改进的灰度级-梯度二维直方图分割算法的基础上,对蚁群的目标搜索进行优化,并通过对其搜索窗口的改进来提升算法的搜索效率。实验结果表明,该算法优于传统的目标分割算法,能够在节省分割时间的同时保持红外目标的提取精度。
[1] Osuna-Enciso V,Cuevas E,Sossa H.A comparison of nature inspired algorithms for multi-threshold image segmentation [J].Expert Systems with Applications,2013,40(4):1213-1219.
[2] Yang H X,Li M,Tan Z H,et al.Maximum scatter difference image thresholding segmentation algorithm based on two-dimensional histogram oblique[J].Laser & Infrared,2014,44(4):463-468.(in Chinese)
杨恢先,李淼,谭正华,等.二维直方图斜分最大散度差阈值分割算法[J].激光与红外,2014,44(4):463-468.
[3] Zhao F,Fan J L,Liu H Q.Optimal-selection-based suppressed fuzzy c-means clustering algorithm with self-tuning non local spatial information for image segmentation [J].Expert Systems with Applications,2014,41(9):4083-4093.
[4] Xiang D L,Tang T,Hu C B,et al.A kernel clustering algorithm with fuzzy factor:application to SAR image segmentation [J].IEEE Geoscience and Remote Sensing Letters.2014,11(7):1290-1294.
[5] Zhao Z X,Cheng L Z,Cheng G Q.Neighbourhood weighted fuzzy c-means clustering algorithm for image segmentation[J].IET Image Processing.2014,8(3):150-161.
[6] Ma Y,Liang H L,Zhang Y N,et al.Bandwidth adaptive mean shift segmentation algorithm [J].Laser & Infrared,2013,43(10):1162-1165.(in Chinese)
马瑜,梁慧琳,张艳宁,等.自适应的均值漂移分割算法[J].激光与红外,2013,43(10):1162-1165.
[7] Huang L W,He D J,Yang S X.Segmentation on ripe fuji apple with fuzzy 2D entropy based on 2D histogram and ga optimization[J].Intelligent Automation and Soft Computing.2013,19(3):239-251.
[8] Wang Z M,Song Q,Soh Y C,et al.An adaptive spatial information-theoretic fuzzy clustering algorithm for image segmentation [J].Computer Vision and Image Understanding.2013,117(10):1412-1420.
[9] Nie F Y,Wang Y L,Pan M S,et al.Two-dimensional extension of variance-based thresholding for image segmentation[J].Multidimensional Systems and Signal Processing,2013,24(3):485-501.
[10]Lan J H,Zeng Y L.Multi-threshold image segmentation using maximum fuzzy entropy based on a new 2D histogram [J].OPTIK,2013,124(18):3756-3760.
[11]Flenner A,Hewer G A,Kenney C S.Two dimensional histogram analysis using the helmholtz principle[J].Inverse Problems and Imaging.2008,2(4):485-525.
[12]Wang J Q,Zhang L,Lu F X,et al.The segmentation of wear particles in ferrograph images based on an improved ant colony algorithm [J].WEAR,2014,311(1-2):123-129.
[13]Wu Y Q,Zhang J K.Thresholding based on maximum entropic correlation of average gray level-gradient two-dimensional histogram [J].Journal of Chinese Computer Systems.2009,30(8):1675-1679.(in Chinese)
吴一全,张金矿.平均灰度级-梯度二维直方图最大相关阈值分割[J].小型微型计算机系统,2009,30(8):1675-1679.
[14]Ghosh S,Kothari M,Halder A,et al.Use of aggregation pheromone density for image segmentation [J].Pattern Recognition Letters.2009,30(10):939-949.
[15]Liu S T,Gao D H,Yin F L.Infrared image segmentation method based on 2D histogram shape modification and optimal objective function[J].Journal of Systems Engineering and Electronics,2013,24(3):528-536.
Infrared image segmentation based on ant colony algorithm and two-dimensional histogram
WEN Kai-feng
(Jiaying University,Meizhou 514015,China)
Existing image segmentation algorithm has the problems of large calculation amount and poor segmentation effect. Aiming at these problems,according to target segmentation characteristics of grayscale-gradient two-dimensional histogram,an infrared image segmentation algorithm based on ant colony algorithm and two-dimensional histogram is proposed. The edges and noise correlation values are introduced into the traditional gray-gradient two-dimensional histogram. In order to extract infrared target rapidly,the image is divided into small windows,and the heuristic function and pheromone update function are redefined according to the optimal segmentation threshold. Experimental results show that the edge of infrared target is clear. The algorithm has a stronger anti-jamming capability and faster computing speed.
segmentation algorithm; two-dimensional histogram; ant colony algorithm; infrared image; threshold
1001-5078(2015)06-0715-07
广东省高等学校学科与专业建设专项资金科技创新项目(No.2013KJCX0171);广东省自然科学基金项目(No.S2013010013307)资助。
温凯峰(1982-),男,硕士,讲师,主要研究方向为图形图像处理,信息物理融合系统等。
2014-09-15;
2014-10-30
TP18
A
10.3969/j.issn.1001-5078.2015.06.024
