基于色散控制的主动锁模掺镱光纤激光器设计
2015-11-24陈淑芬卢骏驰邹正峰孟彦斌
李 根,陈淑芬,卢骏驰,付 雷,邹正峰,孟彦斌
(北京理工大学光电学院,北京 100081)
·激光器技术·
基于色散控制的主动锁模掺镱光纤激光器设计
李 根,陈淑芬,卢骏驰,付 雷,邹正峰,孟彦斌
(北京理工大学光电学院,北京 100081)
设计了一种基于色散控制的相位调制锁模掺镱光纤激光器。针对相位调制锁模中模式跳变现象,基于非线性薛定谔方程,建立了光脉冲在光纤激光器系统中演变的数学模型,通过数值仿真研究了色散对脉冲稳定性的影响。在光纤环形腔中加入光子晶体光纤实现色散补偿,解决了输出脉冲在两个相位差为π的模式间跳变引起的不稳定问题。在稳定锁模的前提下,进一步分析了激光器关键参数(非线性系数、小信号增益系数、调制频率和调制深度)对输出脉冲时域特性的影响。结果表明,在腔内平均色散为-19 ps2/km时,激光器工作在稳定锁模区域,产生重复频率4.918 GHz,脉宽2.54 ps的锁模脉冲,这对于后续实验中的优化设计具有指导性意义。
主动锁模;相位调制;掺镱光纤;色散控制;光子晶体光纤
1 引 言
主动锁模掺镱光纤激光器是近年来发展起来的一种新型脉冲激光器,因其具有转换效率高,重复频率可调,输出脉冲宽度短的特性[1-3],而被广泛运用于医疗、工业加工和大功率脉冲激光器种子源等领域[4-6]。
主动锁模技术通常在环形腔中采用电光调制器实现模式的相位锁定来获得脉冲输出的。与被动锁模技术相比,主动锁模技术的优势是能获得更高能量(pJ到nJ量级)的脉冲输出和更高的重复频率(10 GHz甚至更高),且脉冲重复频率可调谐[7-9]。主动锁模技术中,调制器件可分为强度调制器和相位调制器。强度调制器需要加直流偏置,而相位调制器不需要,由此可避免直流偏置波动所带来的不良影响[10]。相位调制锁模技术存在的问题是输出脉冲在两个相位差为π的脉冲时间序列之间跳变[11]。
本文针对脉冲跳变产生的原因进行了研究,建立了光波模式在光纤激光器系统中传输的数学模型,通过数值仿真得到了不同腔内平均色散值情况下的脉冲时域分布,得出不同色散值对抑制脉冲跳变的作用,在稳定锁模的基础上进一步讨论了腔内各参数对输出脉冲宽度的影响。
2 系统结构
锁模掺镱光纤脉冲激光器结构如图1所示,它由980 nm半导体激光器(LD),980/1060 nm波分复用器(WDM),掺镱光纤(YDF),耦合输出器(OC),偏振控制器(PC),LiNbO3电光相位调制器(PM),光子晶体光纤(PCF)和光隔离器(ISO)组成。
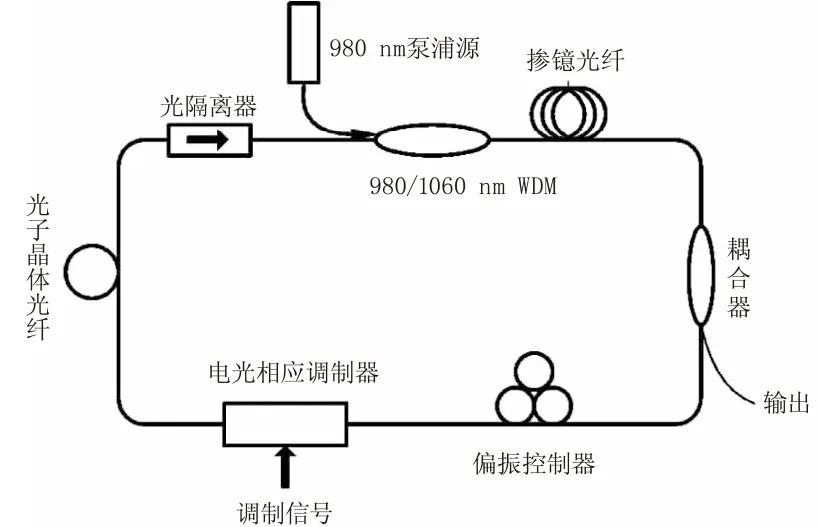
图1 主动锁模掺镱光纤激光器结构
使用波长为980 nm的半导体激光器作为泵浦源,通过980/1060 nm波分复用器将泵浦光耦合入掺镱光纤。本系统选用的是高掺杂浓度的掺镱光纤,能够提供足够大的增益。耦合输出器的输出耦合比为0.1。由于选用了单偏振LiNbO3电光相位调制器,需要使用偏振控制器将输入光偏振态调整到与调制器一致。在1060 nm处,掺镱光纤和单模光纤的色散为正,选用的空心光子晶体光纤具有大的负色散和极小的非线性,能够在不引入额外非线性的情况下进行色散补偿。
3 数学建模
光纤环形腔内脉冲演化过程如图2所示。使用自洽场法对锁模掺镱光纤脉冲激光器系统进行数学建模,让初始光信号依次通过掺镱光纤、单模光纤、相位调制器和光子晶体光纤,分别考虑环形腔中每个器件对光场的作用,循环往返若干次之后得到光场的稳态解。自洽场法基于环形腔的实际结构,能够更加准确地求解出光脉冲在腔中的演化过程。

图2 脉冲演化过程流程图
用非线性薛定谔方程(NLSE)来描述光脉冲在普通光纤中的传输过程:
(1)
式(1)适用于脉冲在单模光纤和光子晶体光纤中传输。式中A代表光场的慢变包络,α代表光纤损耗,β2代表光纤群速度色散系数,γ代表光纤的非线性系数,在图1的系统中这些参数分别对应着单模光纤和光子晶体光纤的有关参数。
脉冲在增益光纤中的传输过程用广义NLSE描述:
(2)
式中,T2反比于增益带宽,即:T2=1/Δωg,光路中所用的掺镱光纤增益带宽为10 nm(Δωg/2π=2.67 THz)。α2表示双光子吸收效应系数,系统中的双光子吸收效应可以忽略不计(α2=0)。g代表饱和增益系数。
掺镱光纤饱和增益的表达式如下;
(3)
其中,g0表示小信号增益系数;Pave为平均功率;Psat为饱和功率,平均功率写作:
(4)
式中,Tm=TR/m,TR为光波沿环行腔传播一周的时间,m为谐波阶数。
相位调制器对光场Ai(t)的调制作用如下式所示:
Ao(t)=eiΔmcos(ωmt+φ)Ai(t)
(5)
在谐波锁模的情况下,ωm=2 πmfc,fc=c/nL,L为总的腔长;n为光纤的折射率;fc表示谐振腔的基频;m为谐波阶数;Δm为调制深度;φ代表调制器和脉冲之间的延迟。
耦合输出器的传递函数可以用如下矩阵表示:
(6)
其中,k为耦合比。
仿真中用到的参数及其意义在表1中列出。
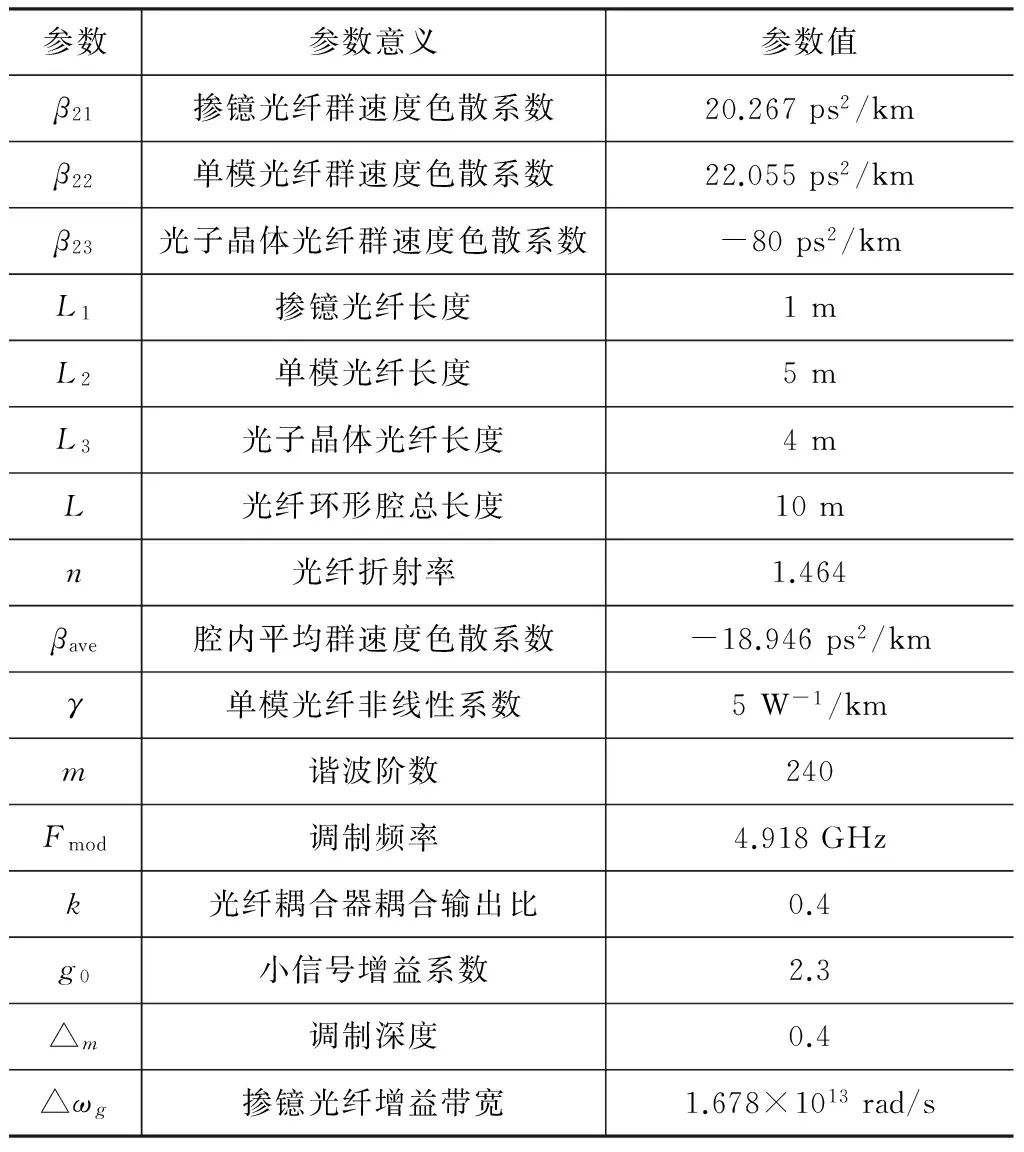
表1 数值仿真中用到的参数及其意义
选取随机噪声作为初始信号,采用分步傅里叶法(SSFM)求解非线性薛定谔方程(NLSE),步长0.1,时间窗口取样点数为1024。每隔100圈记录一次脉冲强度,选取的最大循环圈数为5000圈。
4 仿真结果与讨论
在相位调制曲线的一个周期内存在着间隔π相位的两个极值点(up-chirp and down-chirp),在这两个特殊时刻光波通过调制器时频移为零,能够形成锁模脉冲,于是环形腔内传播着两串相位差为π的脉冲序列,它们之间互相竞争,对锁模形成了干扰,相位调制锁模激光器的输出脉冲容易在这两个状态之间跳变。图3是根据上一节中数学模型,在腔内色散为零时得到的仿真结果,图3(a)为脉冲在腔内的演化过程图。图3(b)为稳态下的一个调制周期内脉冲时域分布图。为了方便观察一个周期内的脉冲形成,取φ=π/2,并且在图中画出了相位调制曲线,结果验证了在调制曲线的一个周期内的确形成了两个脉冲,对应出现在调制曲线的两个极值点处。
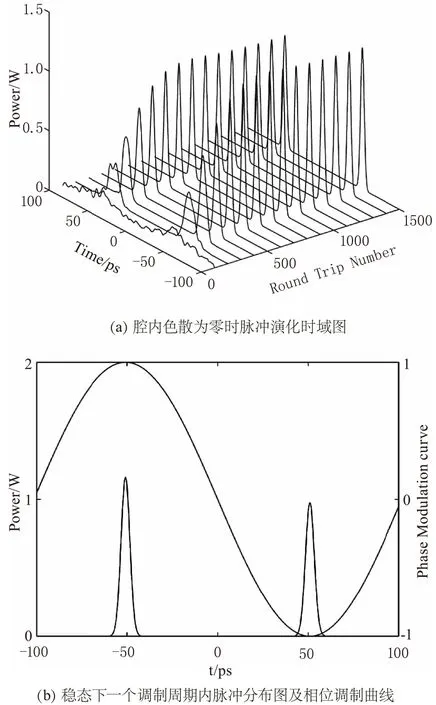
图3 腔内色散为零时的仿真结果
图3表明在腔内色散为零的情况下,存在着2个脉冲序列的竞争,无法得到稳定的锁模脉冲输出。逐步增大腔内平均色散,某一个脉冲会在演化中逐渐得到抑制。图4(a)为脉冲演化过程,图4(b)是最终形成的脉冲时域分布。此时腔内平均色散值βave为-6.9458 ps2/km。
进一步增大腔内色散,最终得到在一个调制周期内只存在一个脉冲,腔内形成了稳定的锁模脉冲序列。图5(a)和(b)中βave为9.0542ps2/km,图5(c)和(d)中βave为-18.946 ps2/km。

图4 βave=-6.9458 ps2/km时的仿真结果
由图3和图4可以看出,随着腔内平均色散的增加,某一个脉冲的幅度逐渐降低,脉宽展宽。当腔内平均色散达到或者超过某个阈值(大于9 ps2/km或者小于-19ps2/km)时,一个调制周期内只存在一个脉冲,另外一个被完全抑制掉。此时激光器输出唯一时间序列脉冲,达到了稳定输出状态。
色散对于跳模的抑制作用机理可以解释如下:在一个调制周期内的两个极值点处,相位调制器给脉冲施加了正啁啾(up-chirp)和负啁啾(down-chirp)。当腔内平均色散为正时,腔内的正色散在时域上展宽了正啁啾脉冲,压缩了负啁啾脉冲,脉冲再次通过调制器时,被展宽的脉冲因为作用时间长,得到了更大量的啁啾,在频域上也得到了展宽,但受限于增益谐振腔的滤波带宽,脉冲能量最后逐渐消失;时域上被压缩的负啁啾脉冲通过调制器时频域展宽量小,展宽量仍在滤波带宽之内,因而最终腔内只存在负啁啾脉冲。而当腔内平均色散为负的时候,负啁啾脉冲得到展宽,逐渐消失;正啁啾脉冲得到压缩,形成稳定的锁模脉冲。
同时腔内还存在着自相位调制作用,在脉冲的中心区域内,自相位调制作用产生的啁啾可以简化为正啁啾。对于正色散腔,这种正啁啾强化了色散带来的展宽效应,一定程度上弱化了压缩效应;对于负色散腔则正好相反;压缩效应被强化,展宽效应被削弱。因此正色散腔产生稳定锁模的色散阈值的绝对值大于负色散腔中的阈值,而负色散腔中脉冲普遍要窄一些。对比图5(b)和图5(d),可以看出仿真结果验证了上述理论分析。
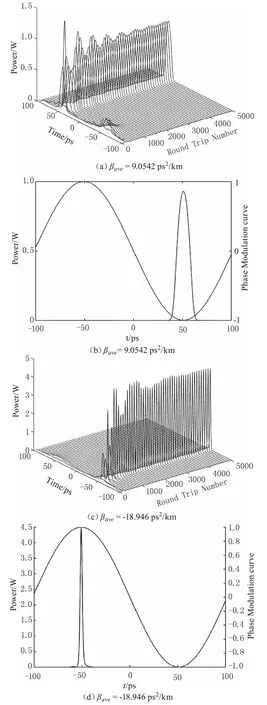
图5 脉冲时域演化图及稳态下一个 调制周期内脉冲分布图
由上面的讨论可以得出,在谐振腔内加入一定色散量的补偿器件能够抑制住腔内的跳模现象。在得到稳定锁模的前提下,为了获取更窄的脉冲,通过仿真进一步研究了色散值变化对脉宽的影响。在仿真中,保持其他参数不变,改变色散值,得到对应的脉宽,图6给出了色散值变化和脉宽的关系曲线。图6(a)中平均色散为负,图6(b)中平均色散为正。
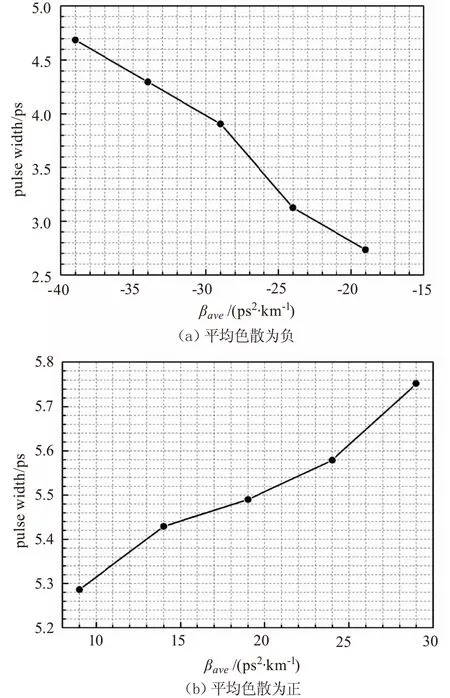
图6 脉宽随色散变化关系图
在负色散区,脉宽随着平均色散值的增大而减小;而在正色散区变化趋势相反,脉宽随着平均色散值的增大而增大。最窄的脉宽为2.5391 ps,出现在平均色散值为-19 ps2/km处。
除了色散之外,影响脉冲宽度的因素还有小信号增益系数(g0)、非线性系数(γ)、谐波阶数(m)和调制深度(Δm)。g0和γ决定了自相位调制的强度,较强的自相位调制作用带来较大的啁啾,增强了色散对脉冲的压缩作用,最终得到更窄的脉冲;m和Δm影响的是调制器的调制效果,随着m和Δm的增大,调制器引入的啁啾量也随之增大,也增加了脉宽压缩的作用。图7给出了βave=-19 ps2/km时脉宽随4个因素变化的曲线。
图7(a)中,脉宽随着g0的增加显著减小。当g0小于0.6时,腔内增益小于损耗,无法产生激光;当g0大于2.4时,过高的非线性导致脉冲分裂;图7(b)中,随着γ的增加,脉宽减小,当γ大于5.5W-1/km时,脉冲同样开始发生分裂。
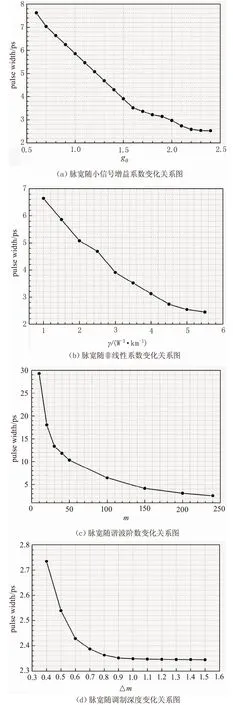
图7 βave =-19 ps2/km时脉宽随4个因素变化的曲线
图7(c)中,脉冲宽度随着m的增大而减小,当m大于150时,脉宽的减小趋于平缓。调制频率为纵模间隔的m倍时,腔内形成了m组超模,彼此之间互相竞争,被称为超模竞争。超模竞争会导致输出脉冲中含有随机噪声,超模噪声随着m的增大而增大。自相位调制作用和光学滤波器的结合形成了一种快速强度相关损耗作用,能够有效地抑制超模噪声。因此在后续实验中,需要在环形腔中加入滤波器。
图7(d)中,Δm小于0.4时,调制器的调制作用太弱,腔内无法形成锁模脉冲。随着Δm的增加,脉宽逐渐减小,当Δm大于0.8时,脉宽的减小同样趋于平缓。调制深度和加在调制器上的驱动电压的幅值有关,过高的驱动电压会导致调制器损坏,同时也对脉宽减小的贡献不大,实验中需要选择合适的驱动电压幅值。
5 结 论
设计了一种基于色散控制的相位调制锁模掺镱光纤激光器,并对其工作机理进行了研究和分析,建立腔内脉冲演化的数值仿真模型。通过该模型锁模激光脉冲输出的仿真分析,确定了系统结构和参数。仿真结果表明,通过引入光子晶体光纤改变腔内色散,在当腔内平均色散超过一定阈值的时候,一个调制周期内只有一个脉冲出现,跳模现象得到了抑制,激光器工作在稳定锁模区域;进一步优化非线性系数、小信号增益系数、调制频率和调制深度等参数,能够压缩脉冲宽度,得到更窄的脉冲。这对后续实验工作有着一定的理论参考意义。本文中用到的仿真模型并没有考虑到由于室温改变、机械震动等因素导致的腔长变化,在实际实验中,需要引入一种反馈机制来保持腔长和对应的调制频率一致,比如再生锁模技术;同时,需要在腔内加入一个合适带宽的光滤波器抑制超模噪声。
[1] B Ortaç,M Baumgartl,J Limpert,et al.Approaching microjoule-level pulse energy with mode-locked femtosecond fiber lasers[J]. Opt.Lett.,2009,34(10):1585-1587.
[2] P Zhou,X Wang,H Xiao,et al.Review on recent progress on Yb-doped fiber laser in a variety of oscillation spectral ranges[J].Laser Phys.,2012,22(5):823-831.
[3] X Zhou,D Yoshitomi,Y Kobayashi,et al.Generation of 28-fs pulses from a mode-locked ytterbium fiber oscillator[J].Opt.express.,2008,16(10):7055-7059.
[4] D A Sidorov-Biryukov,K A Kudinov,A A Podshivalov,et al.Widely tunable 70-MHz near-infrared source of ultrashort pulses based on a mode-locked ytterbium laser and a photonic-crystal fiber[J].Laser Phy.Lett.,2010,7(5):355.[5] J Swiderski,D Dorosz,M Skorczakowski,et al.Ytterbium-doped fiber amplifier with tunable repetition rate and pulse duration[J].Laser phys,2010,20(8):1738-1743.[6] Y Izawa,N Miyanaga,J Kawanaka,et al.High power lasers and their new applications[J].Journal of the Optical Society of Korea,2008,12(3):178-185.
[7] K S Abedin,N Onodera,M Hyodo.Generation of a 64-GHz,3.3-ps transform-limited pulse train from a fiber laser employing higher-order frequency-modulated mode locking[J].Opt.Lett.,1999,24(22):1564-1566.
[8] N G Usechak,G P Agrawal,J D Zuegel.Tunable,high-repetition-rate,harmonically mode-locked ytterbium fiber laser[J].Opt.Lett.,2004,29(12):1360-1362.
[9] K Koizumi,M Yoshida,T Hirooka,et al.10 GHz,1.1 ps optical pulse generation from a regeneratively mode-locked Yb fiber laser in the 1.1 μm band[J].Opt.Express.,2011,19(25):25426-25432.
[10]M Nakazawa,E Yoshida,K Tamura.10 GHz,2 ps regeneratively and harmonically FM mode-locked erbium fibre ring laser[J].Electron.Lett.,1996,32(14):1285-1287.[11]N G Usechak,G P Agrawal,J D Zuegel.FM mode-locked fiber lasers operating in the autosoliton regime[J].IEEE J.Quant.Electron.,2005,41(6):753-761.
Design of active mode-locked ytterbium-doped fiber laser based on dispersion control
LI Gen,CHEN Shu-fen,LU Jun-chi,FU Lei,ZOU Zheng-feng,MENG Yan-bin
(School of Optoelectronics,Beijing Institute of Technology,Beijing 100081,China)
A kind of frequency-modulation mode-locked ytterbium-doped fiber laser is designed.Focused on mode-hopping phenomenon in frequency-modulation mode-locked pattern,the mathematical model of light pulse evolution in fiber laser is established based on nonlinear Schrödinger equation,and the effects of dispersion on the pulse stability are studied through numerical simulation.The mode hopping problem,that output pulses tend to jump back and forth between two modes which are 180° apart relative to each other,is solved by employing a photonic crystal fiber in the ring cavity for dispersion compensation.In the premise of stable mode-locking,the effects of several critical parameters(such as the nonlinear coefficient,the small signal gain coefficient,the modulation frequency and the modulation depth) on time-domain characteristics of the output pulses are analyzed.The analytical result shows that the fiber laser works in stable mode-locking region and produces stable output pulses with 2.54 ps pulse width and 4.918 GHz repetition frequency when the average dispersion is -19 ps2/km.The simulation data play a guiding role in optimal design for the later experiments.
active mode-locking,frequency modulation,ytterbium-doped fiber,dispersion control,photonic crystal fiber
1001-5078(2015)06-0625-06
李 根(1990-),男,硕士在读,研究方向为光纤激光器。E-mail:425091194@qq.com
2014-10-13
TN248
A
10.3969/j.issn.1001-5078.2015.06.006
