自然逻辑与不自然逻辑刍议——以命题逻辑为例
2015-11-24肖翀
肖 翀
(中央财经大学 文化与传媒学院,北京 100081)
自然逻辑与不自然逻辑刍议——以命题逻辑为例
肖 翀
(中央财经大学 文化与传媒学院,北京 100081)
在逻辑中,自然演绎方法与公理方法是研究各种逻辑词之间的推理规律的两种不同的研究方式.本文以命题逻辑中的推出关系为例,研究了逻辑推理演算在自然逻辑系统与不自然逻辑系统中的特点,总结了自然演绎方法与公理方法的区别与联系,认为自然逻辑更契合人类思维习惯,更易于接受.
自然逻辑; 不自然逻辑; 公理方法; 自然演绎方法
在命题逻辑系统中,研究各种逻辑词的推理规律的过程,对于包括否定词(¬)、合取词(∧)、析取词()∨、蕴涵词()→和等值词(↔)为研究对象的一个形式语言,可以采取不同的研究方法.理论上讲,这些研究方法得到的推出关系的集合可以是相同的或者等价.但是,对于某些逻辑词,在推演它们的全体推出关系形成的集合时,由于其出发点、复杂程度各不相同,尤其在是否有明确的推演目标、明确的推演步骤等方面,不同的研究方法大异其趣.
命题逻辑中的研究方法有很多.如:可以运用自然逻辑方法从一个推理规则集合出发来构造逻辑的形式系统,把关于某些逻辑词的推出关系纳入这个系统; 可以通过公理方法从一个公理集合和一个推理规则集合来建立逻辑演算; 可以通过范式方法来研究一个公式或公式集合的各种性质,特别是该公式或该公式集合的所有逻辑后承; 还可以通过其真值表方法运用一个规则集合来逐个构造某个公式或公式集的反驳,以研究这个公式或公式集是否存在推出关系等等.
公理化方法是自现代逻辑创立以来最常见的研究方式,能够通过公理刻画某些逻辑词的性质和它们之间的关系,其作用是任何人都不可否认的.公理化方法是从初始概念和公理出发,利用它们定义其他一切概念以及推演出其他一切定理的演绎方法.对初始概念、公理、定义、推理规则、定理等应用公理化方法构建的演绎体系,称为公理系统.公理化方法是以推导逻辑定理为己任的,其过程往往是探索性、试错性的,比较复杂[2],是以逻辑定理(逻辑真命题)来不自然地刻画逻辑推出关系的.这种刻画方式与人类在长期的日常生活中养成的逻辑推演习惯不符合,因此也被称为不自然的逻辑.
自然演绎来源于对希尔伯特演绎系统中的不满.早在1926年,在波兰的一系列逻辑研讨会中就有逻辑学家提出了要对逻辑进行更加自然的处理.20世纪30年代,德国逻辑家G·根岑和波兰逻辑家C·雅斯科夫斯基提出了“希望构造尽可能紧密于实际推理的一种形式化主义.所以提议了‘自然演绎演算’.”,构造了完全以推理规则集合代替公理来建立逻辑的形式系统,即以推理规则来表示前提与结论之间的推出关系或推理规律,这是比较符合人类实际思维过程的,又叫做自然逻辑.
在命题逻辑中,研究各种逻辑词的推理规律时,可以依据其不同的特点采取不同的研究方法.人类研究推理时该如何取舍形式语言相同的公理化方法与自然演绎方法呢?回答这个问题,必须分析公理化方法与自然演绎的异同.
若M根据集合Φ断定ϕ,则称M为一个从Φ到ϕ的推理,其中Φ称为前提集,ϕ称为结论.这就是直观意义上的推理,一个非常自然的演算,即自然逻辑.当然,日常推理中的前提集Φ总是非空的,当Φ是空集的时候,这样的推理并没有本质不同.推理的有效性是由推理形式决定的,着重对推理进行语形刻画.以条件证明为例:如果Γ,A├B,那么Γ├A→B.其中Γ是前提集合{A1,A2,…,An}(n≥1),在条件证明的推理过程中运用蕴涵词引入规则(→+):从前提A1,A2,…,An可以推演出B,那么从前提A1,A2,…,An可以推演出A→B,同样,前提A1,A2,…,An-1可以推演出An→(A→B),依此类推,前提A1可以推演出A2→(A3→…→(An→(A→B))…),前提∅可以推演出A1→(A2→…→(An→(A→B))…),.这时,它描述了一种非常特殊的推理——前提集为空的推理.在日常思维中,这种推理几乎不能称为推理,因此是一种所谓的“不自然逻辑”.由此看到,自然逻辑与不自然逻辑之间是可以相互转化的.
公理化方法的出发点是一些初始概念和公理,并且用公理代替了自然逻辑中绝大部分基本的推导规则,推理必须使用公理或已证明的定理.自然演绎是从给定或假设的前提出发,仅仅依据一系列的推理规则,得出这些前提的逻辑结论.也就是说,自然演绎不需要任何公理,只是以假设为前提(公理也作为一种基本假设),这些假设前提可以随时引进,只有具有保真性的推理规则.值得注意的是,公理化方法通常是不带假设的证明,仅把少数几条公理(即不加证明的命题或公式)作为推理的出发点或前提,除了系统中已给定的公理,定义和已证明的定理外不得引用任何附加或隐含的前提.这是自然逻辑与不自然逻辑相比,最明显的区别.通过下面的例子可以更清楚看到这一区别.
例 证明(¬p→q)→(¬q→p).
证法1 (公理方法①在本文运用的公理方法是在罗素公理系统中的,其基本公理有6条:I.真命题所蕴涵的命题是真命题; II.(p∨p)→p ; III.q→(p∨q); IV.p∨q→(q∨p); V.[p∨(q∨r)]→[q∨(p∨r )]; VI.q→r→(p∨q→p∨r ).证明过程中右角的定理序号是金岳霖的《逻辑》一书中的序号.)
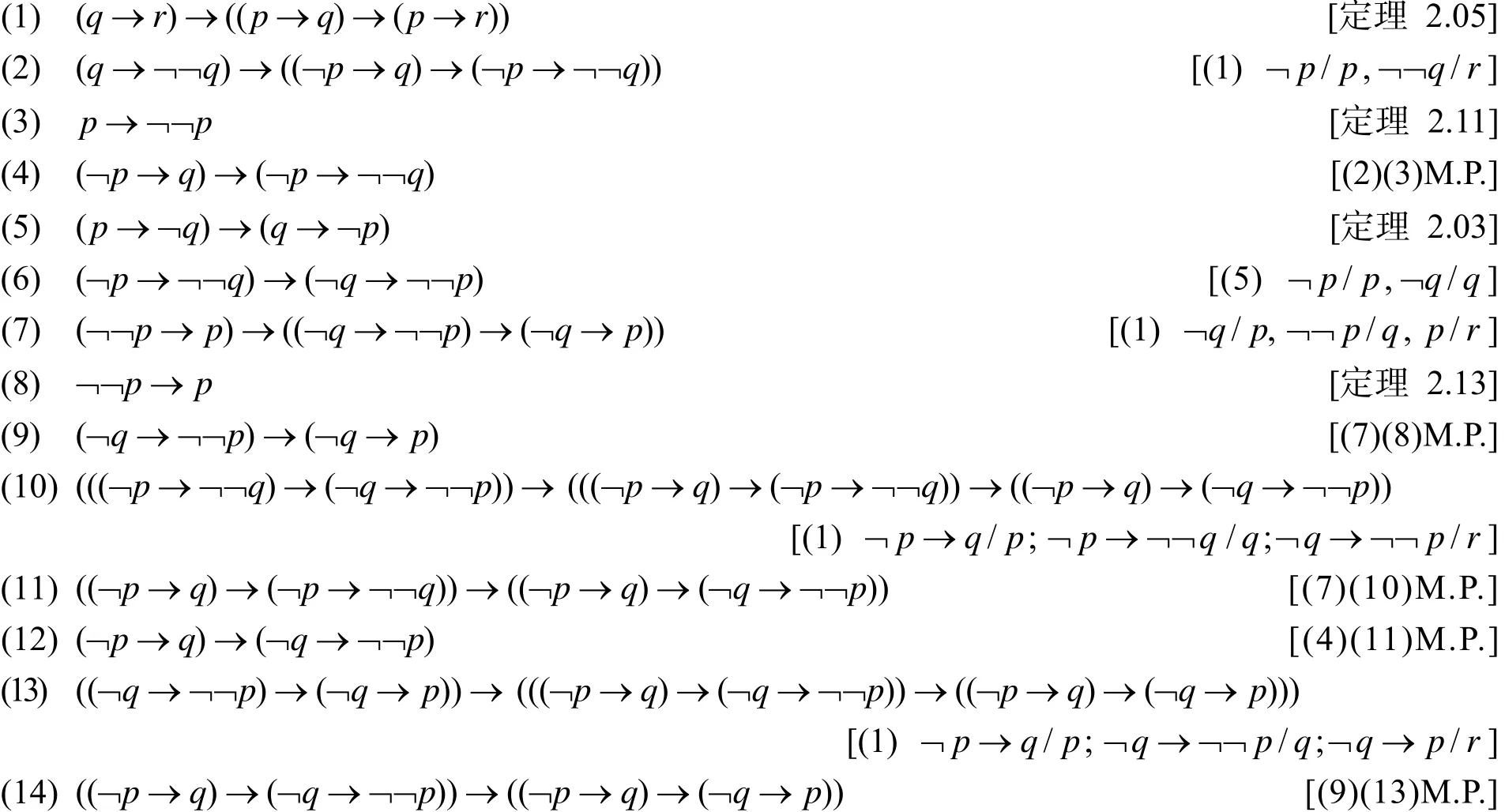
从公理方法的整个过程中可以看出,证明的出发点是公理,依据是推理规则中的肯定前件规则(M.P.)和代入规则.毫不夸张地说,整个推理过程复杂、冗长,让人望而生畏.为了降低公理方法的复杂性,通常在系统中先由公理证明演绎定理:如果A├B,那么∅├A→B,再运用演绎定理引入假设推演逻辑定理.
再看一下自然逻辑的两个方法.
证法2 (自然逻辑方法1)

自然演绎方法与公理方法方法相比,整个过程直观、简短,也让人乐于接受,不仅丝毫没有减少公理方法的严谨、精确的特点,而且大大增强了形式推演能力,缩短了形式推演的过程,在推理步骤、推理方法、推理技巧上更简便、灵活、多样,也更易于被人们掌握.
在自然逻辑的方法中,有不借助假设,只依据推理规则从已知前提逐步得出结论的形式推演,这种不引入假设的证明方法叫直接证明; 也有通过引入辅助假设(真前提)并在最后引入蕴涵词(+→)以消去辅助假设的形式推演,也叫条件证明,如证明2的推导过程中第(1)行是已知前提A1,在第(2)行引入假设H1,在第(5)行引入了蕴涵式qp¬→从而消去了假设H1; 还有通过引入辅助假设(假结论)并在最后推导出逻辑矛盾从而否定假设(¬_ )以消去辅助假设的形式推演,称之为间接证明或反证法,如证明3的推理过程中第(2)、(3)行是引入的假设H1、H2,在第(5)行推出了逻辑矛盾qq∧¬从而消去假设前提H2,在第(6)行引入蕴涵式消去H1.自然逻辑方法可以随时引进一个假设作为推理出发点,再运用蕴涵词引入规则(+→)和否定消去规则(¬_ )把引入的假设从前提中消去,推出的结论就不再依赖于引入的临时性假设,仅依赖于已知前提.
换句话说,在自然逻辑中侧重刻画的是逻辑推论,只与推论证明的形式有关.结论是否具有保真性,与假设的真假无关,在已知前提为真时,仅看它的推出过程是否处处合乎引入或消去规则,这明确地展示了命题之间内在的、稳定的、必然的逻辑联系[4].
自然演绎方法类似于自然科学中常用的证明程序,如定律、定理的证明,尤其在数学学科中.在逻辑演算及日常思维中具有较高的实用性.例如在平面几何中的证明,是由“已知”,“求证”和“证明”三个部分构成的.其中的“已知”就相当于自然逻辑中的“给定的前提”,“求证”就相当于“结论”,而“证明”就是从前提推出结论的逻辑推理.在证明过程中,所作的辅助线相当于“(条件证明的)假设的前提”,而以结论的否定作为假设,就是运用反证法进行证明.在日常生活中,往往也是从前提(包括省略的前提)出发,经过推理得出结论,或者说,为一个主张寻求支持它的理由.只不过由于自然语言的表达方式灵活多样,需要经过仔细地分析才能发现前提和结论、主张和理由之间的推理(推出、推论、推演)关系.
同时,自然逻辑系统也突出了形式逻辑与其他形式理论之间的区别,如几何学、生物学等,因为在这些学科中,除了要求逻辑推理规则的特有基础之外,还要求与它们研究的领域有关的具体的公理.
人类进行推理的目的,是为了从真前提得到真结论,即逻辑真.逻辑的着眼点是语义推出关系,表现形态是语法推出关系[3].不自然逻辑是现代逻辑创立以来直到今天最常见的逻辑系统,且公理化方法对逻辑研究的作用是任何人都不可否认的.但是,公理化方法容易把人们的注意力从论证的有效性转移到公式的逻辑真值问题上,从而偏离了逻辑的中心问题.
自然逻辑作为一枝后起之秀,更好地反映了逻辑的主要问题,即论证的有效性问题.自然演绎方法突出了逻辑是研究有效推理规则的,把逻辑真的语义刻画看成前提为空的推理关系的一种特殊情况,契合人类思维的习惯,就其在日常思维中的逻辑推理的实用性来说,它比公理化方法更具有优越性,在逻辑学的普及中具有重要意义.
[1] 李小五.什么是逻辑[ J].哲学研究,1997,( 10):76~80
[2] 袁正校.关于现代逻辑教学中若干问题的思考[ J].重庆工学院学报,2006,20(1)
[3] 何向东,袁正校,郭泽深.逻辑学教程[M ].北京:高等教育出版社,2004
[4] 袁正校.逻辑学基础教程[M].北京:高等教育出版社,2007
[5] 苏珊·哈克.逻辑哲学[M].北京:中国商务出版社,2003
Discussion on Natural Logic and Unnatural Logic:Taking Propositional Logic as an Example
XIAO Chong
(College of Culture and Communication,Central University of Finance and Economics,Beijing 100081,China)
Natural deductive and axiomatic are different methods in study of inference rule of logical words.In this paper,two methods are studied in logical deductive calculus by taking deducing relation in propositional logic as an example.As a conclusion,natural logic conforms to the human thinking habits by contrast unnatural logic,and can be acceptable by people.
natural logic; unnatural logic; axiomatic approach; natural deduction method
B813; O141
A
1672-5298(2015)01-0010-03
2014-11-01
肖 翀(1985- ),女,湖南华容人,中央财经大学文化与传媒学院硕士研究生.主要研究方向:现代逻辑及其应用
