列车蛇形运动状态下轮轨接触特性分析

魏云鹏，吴亚平，段志东，许贵满，王良璧

(1.兰州交通大学土木工程学院，兰州 730070; 2.兰州交通大学机电工程学院，兰州 730070)

列车蛇形运动状态下轮轨接触特性分析

魏云鹏1，吴亚平1，段志东1，许贵满1，王良璧2

(1.兰州交通大学土木工程学院，兰州 730070; 2.兰州交通大学机电工程学院，兰州 730070)

为了分析列车在蛇形运动状态下轮轨接触区域的形状、面积、轮轨接触应力和Mises应力的特性，根据有限元理论并结合ANSYS有限元软件，建立包含一个轮对的轮轨系统有限元模型，计算分析轮轨接触特性与轴重和轮对摇头角之间的关系，计算结果表明：轮对摇头角对接触特性的影响不是很明显，而轴重和轮对中心横移量对轮轨接触斑的面积和形状有着显著的影响；接触斑的形状不同于用Hertz理论得到的椭圆形接触斑。

轮轨关系；蛇形运动；接触特性；有限元

重载列车在交通运输工程中由于其运输能力高，运输方便快捷，并且运输成本低廉，对国民经济起着至关重要的作用。世界各铁路强国在机车车辆和轨道结构技术方面进行了积极研究，把发展铁路运输技术作为重点项目。由于列车载重越来越大，这将会造成轮轨的严重损伤，这一方面增加了铁路运营的养护维修成本，另一方面也增加了运营的不安全性；同时，列车运营的非线性临界速度往往低于其设计值[1]，这将更容易出现蛇形运动，即列车产生摇头、侧滚和横摆等振动现象，这将也会引起轮轨接触的损伤。国内外有许多学者对轮轨接触特性进行了研究，郭火明等人[2]在现场测试了重载铁路损伤钢轨，分析了损伤机理，并且探讨了疲劳裂纹的萌生和扩展；刘鹏飞等人[3]研究了30 t轴重条件下，LM型车轮踏面和不同类型钢轨匹配时轮轨接触的几何关系，并分析了不同轨底坡对轮轨接触的影响；Tomasz Kuminek 和 Krzysztof Anioek[4]用有限元方法建立了二维和三维的轮轨模型，计算了轮轨接触应力，并比较了不同网格划分和材料参数对接触应力的影响；Wu Fengqi[5]结合有限元计算数据和实测结果，分析比较了轮轨非线性接触应力，同时指出了理论计算结果和实测数据之间的差异；Mehmet Ali Arslan和uz Kayabasl[6]用有限元法建立了三维的轮轨接触模型，计算分析了轮轨接触区域的应力和应变，并与已有的数据进行了对比。杨丽娟等人结合具体的实例分析对比了DP和ECP两种重载技术的不同[7]，并对不同的情况给出了合理的方案。另外还有一些学者对重载条件下机车的动力学特性和大跨度钢桁梁桥面系的选择进行了研究分析[8-9]。

以上的研究揭示了轮轨接触的一些特性，但没有对列车在蛇形运动情况下的轮轨接触面积、接触压应力和轮轨接触区域的应力做全面具体的分析，根据有限元理论，建立包含一组轮对的三维轮轨接触模型，并且考虑了轨道结构对轮轨接触区域的影响，系统分析了列车在蛇形运动情况下轮轨的接触特性。

1 有限元模型

1.1 轮轨系统三维有限元模型

本模型选用JM型车轮踏面和S形辐板，踏面依据原铁道部发布的机车车辆车轮踏面作图方法建模[10]，钢轨为CHN60型钢轨，轨底坡度为1∶40。

依据大型结构分析软件ANSYS，建立了三维的轮轨接触模型，模型中包括车轴、轮对、钢轨、橡胶垫板、混凝土轨枕和地基，轨道结构总长度为4.35 m；由于在接触区域的应力很大，同时为了避免增加单元的数量，只在轮对与钢轨接触区域用20节点的186单元模拟，模型中的其他部件用8节点的185单元模拟，接触单元为174单元，目标单元为170单元，并且在疏密网格的连接处用多点约束的方法在节点之间建立了联系，轮轨之间的接触为标准的接触状态；本模型共有73 664个单元，130 921个节点，计算模型如图1 所示。

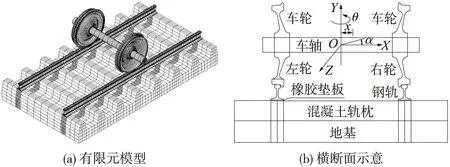
图1 有限元模型

1.2 计算参数

在轮轨接触表面由于应力很大，列车长期运营后，轮轨表面材料不断被强化，因而选用文献[11]中的轮轨材料的本构关系，该本构关系为双线性随动强化模型，钢轨和车轮的泊松比为0.3，密度为7 800 kg/m3；车轴泊松比0.28，弹性模量为207 GPa，密度7 800 kg/m3；橡胶垫板刚度为100 MN/m；混凝土轨枕泊松比为0.2，弹性模量为39.8 GPa，密度为2 500 kg/m3；根据文献[12]地基刚度取为800 MPa/m。

2 计算结果

列车蛇形运动时，轮对侧滚角α，轮对摇头角θ和轮对中心横移量X如图1(b)所示，轮对侧滚角和轮对中心横移量之间的关系依据文献[13]确定。为了获得不同轴重下，轮轨接触面积、接触应力和轮轨的Mises应力与轮对摇头角θ和轮对中心横移量X之间的关系，模型中θ=0°～0.9°，X=0～10 mm，列车的轴重F加载从160 kN开始，最终轴重为320 kN，轴重增量为40 kN。计算中分别先给定θ值，再取定X，最后计算在不同轴重F作用下的接触特性，同时，为了保证轮轨准确接触，不断对α进行了调整。整个计算模型在Intel(R)Core(TM) i7-4770/CPU(3.4 GHz)/RAM(32.0 GB)的台式机上连续计算9 d，得到了轮轨接触的各种特性。

2.1 接触形状和面积

列车在蛇形运动时，轮轨接触位置时刻在发生变化，其接触斑的形状和面积也各不相同，也不同于用Hertz接触理论所得到的形状和大小，图2给出了θ=0.6°，X=6 mm，F=200 kN时左右接触斑的形状。

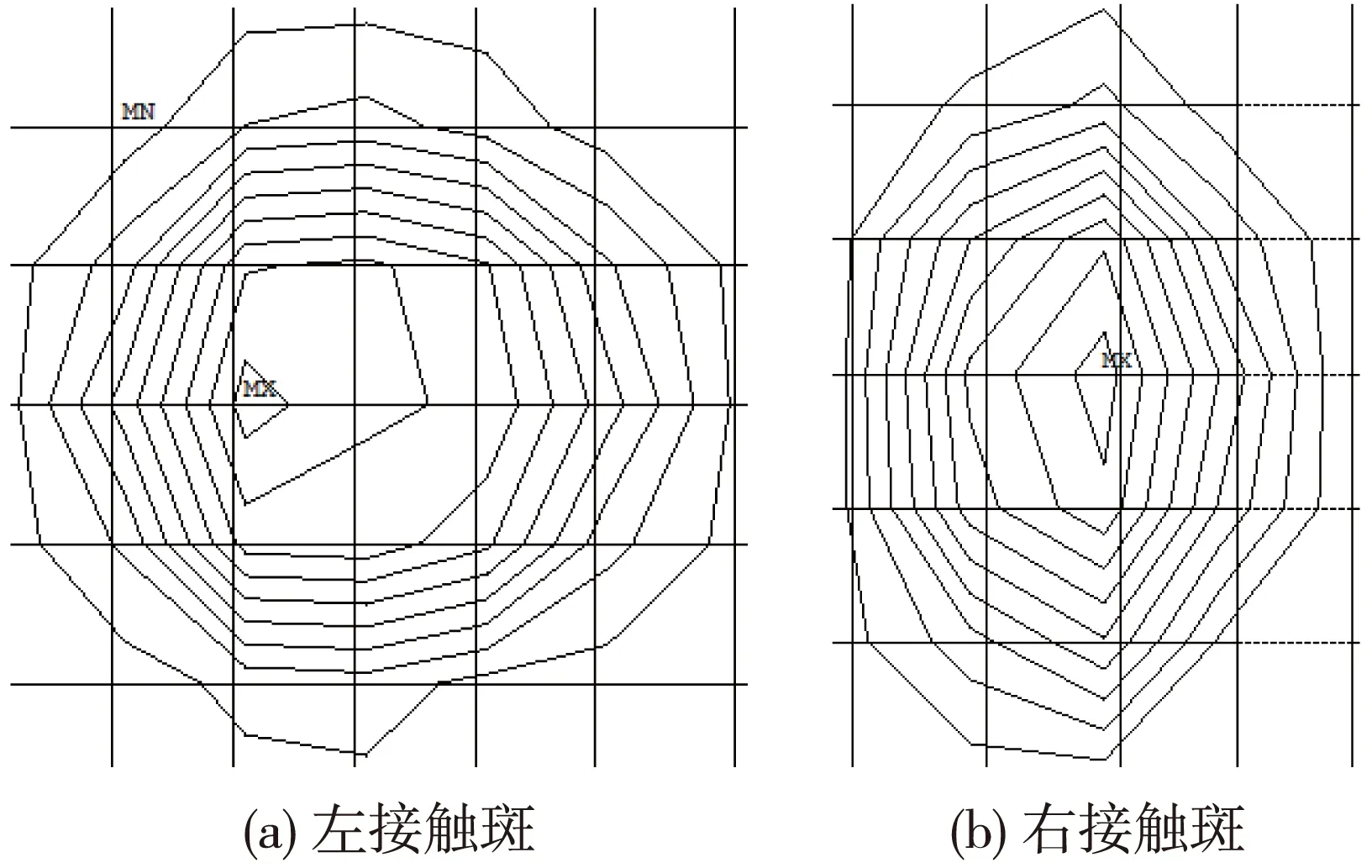
图2 接触斑形状

从图2中可以看出，左右接触斑的形状和面积是各不相同的，实际的轮轨接触斑的形状明显的不同于用Hertz理论得到的椭圆形接触斑，并且这种差异随着轮对摇头角和横移量的变化而变化。

图3表示的是轮对中心横移量为8 mm，摇头角θ=0°和θ=0.3°时，左接触斑面积AL和右接触斑面积AR与轴重之间的关系。从图中可以看出来，接触斑面积随着轴重的增加而增大，但左右接触斑面积的大小是与轮对摇头角有关的，从计算的数据看，当θ=0°时，其左接触斑面积普遍小于右接触斑的面积，但当θ≠0°时，右接触斑面积小于左接触斑的面积。最大接触斑面积出现在左接触处，其值为390.4 mm2，此时θ=0.3°，X=8 mm，F=320 kN时；当θ=0.9°，X=6 mm，F=160 kN时，得到了最小的接触斑面积，最小的接触斑面积出现在右接触处，其值为189.8 mm2。

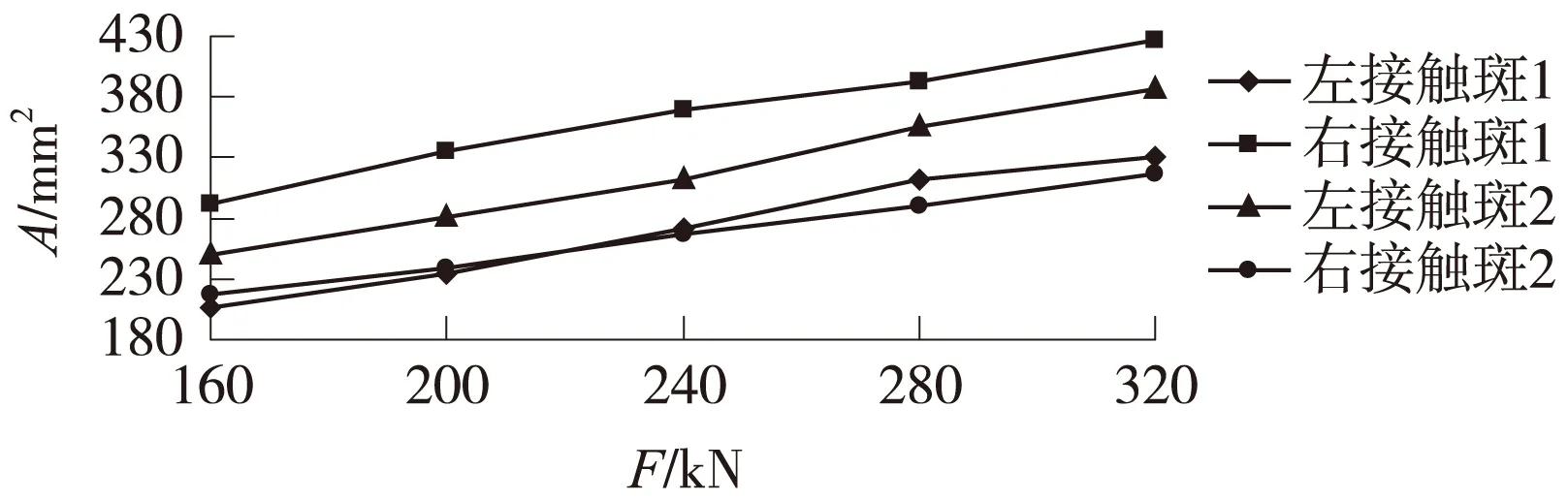
图3 接触斑面积与轴重之间的关系

图4表示的X=6 mm，F=280 kN时，接触斑形状和位置的随轮对摇头角的变化示意图。从该图中可以看出来，左右接触斑的形状明显不同，左右接触斑随轮对摇头角变化的运动轨迹不是很明显，这主要是轮对摇头角较小，钢轨几何型面在轮轨接触位置处变化较小的缘故。

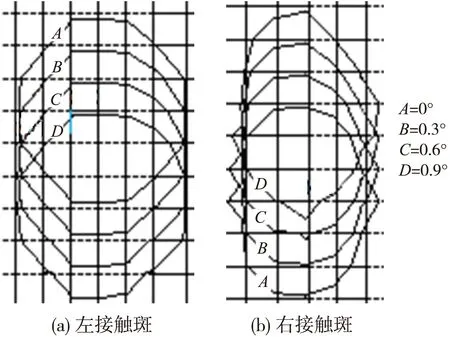
图4 接触斑形状和位置随摇头角的变化

2.2 接触应力

轮轨接触压应力在ANSYS中是通过法向接触刚度和接触间隙的大小计算的[14]。图5给出了θ=0.9°，X=6 mm时，轮轨接触应力与轴重之间的关系。

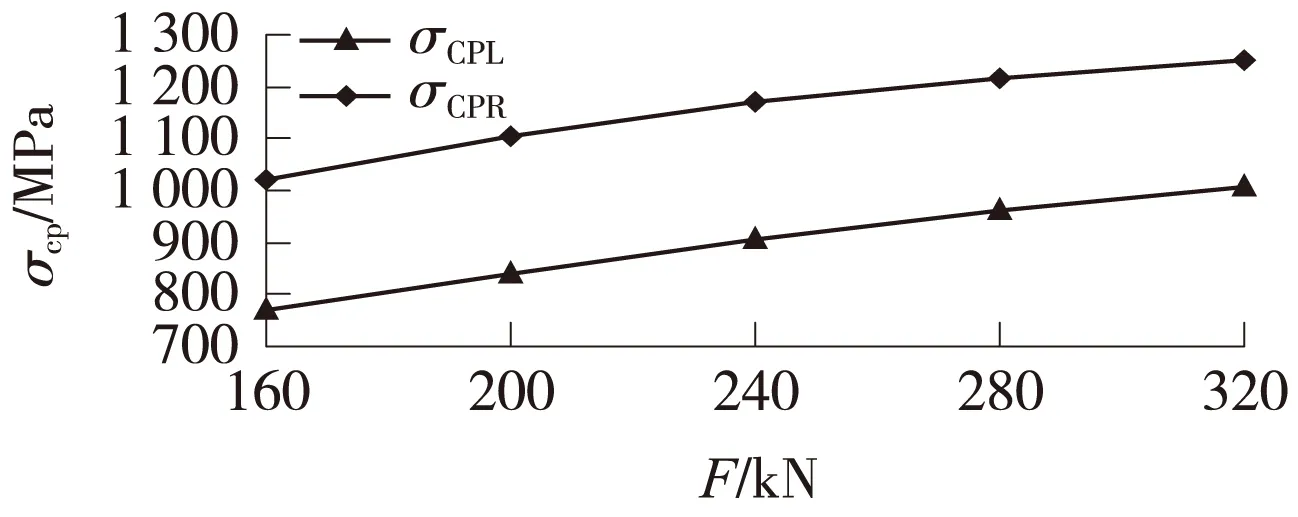
图5 接触应力与轴重之间的关系

从图5中可以看出来，接触应力随着轴重的增加也是逐渐增大的。在计算中由于设定的轮对中心偏移量始终是大于零的，所以左面接触应力σCPL都是小于或者等于右面接触应力σCPR的，但是蛇形运动受载重、车速、轨道结构和外部因素等的影响，其运动很大程度上是随机的，接触应力也是随机变化的。

图6表示的是X=8 mm，F=320 kN时，左右接触斑的最大接触应力与轮对摇头角之间的关系。从该图中可以看出来，左右接触斑的最大接触应力随摇头角的增大变化很缓慢，这主要是因为当轴重不变时，轮轨的接触位置和形状随摇头角增大变化较小。结合图5和图6可以看出，影响接触应力的主要因素是列车的轴重，轮对摇头角对其影响不明显。计算的结果显示最大的接触应力为1 251.7 MPa，最小的为723.4 MPa。

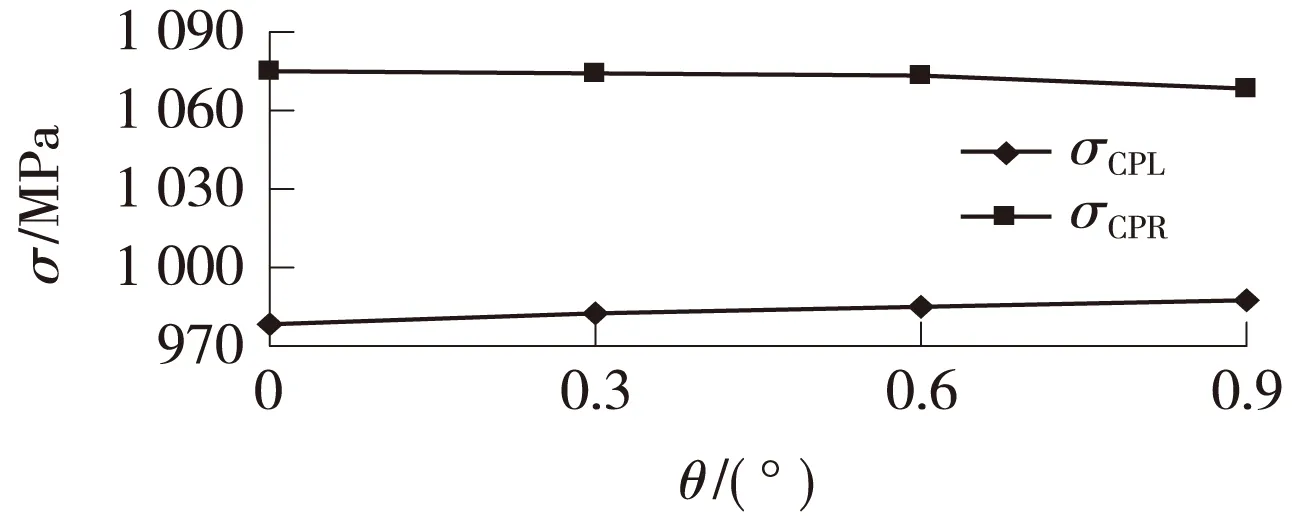
图6 最大接触应力与轮对摇头角的关系

2.3 接触区域Mises应力

Mises应力遵循材料力学中的第四强度理论，用来衡量弹塑性材料在复杂应力状态下一点的应力水平。图7表示的是θ=0.6°，X=8 mm时，左右车轮(σWL，σWR)和左右钢轨(σRL，σRR)最大Mises应力随轴重的变化关系。

图7 最大Mises应力与轴重之间的关系

从图7中可以看出，轮轨Mises应力都是随轴重的增加而增加的。在计算中发现，右面钢轨接触区域最大的Mises应力比左面的大，而左面轮子的最大Mises应力和右面的相比可大可小，这主要是由于轮对蛇形运动时(本文中θ≤0.9°，X≤10 mm)，接触斑在钢轨表面的分布范围是一定的，而车轮的外形是由多段不同曲率半径的圆弧线所组成的，其接触区域随着轮对摇头角和中心横移量的变化始终在变，因而其Mises应力也是变化的。

图8表示的是X=2 mm，F=240 kN时，左右车轮的最大Mises应力随轮对摇头角的变化关系。图8显示左轮最大Mises应力随着轮对摇头角的变化几乎不变，而右轮的随摇头角的增大其值缓慢增大，这说明轮对最大的Mises等效应力不随摇头角的变化而显著变化。对于钢轨的最大Mises应力也有相似的规律。

图8 车轮最大Mises应力与轮对摇头角之间的关系

图9表示的是θ=0.6°，X=4 mm，F=320 kN时右面轮轨接触区域的Mises应力等值线图，Mises应力在接触点附近很大，向外很快衰减，同时在计算中发现钢轨的最大的Mises应力发生在距离轮轨表面0.5～4 mm的次表层位置，这与文献[12]的结果是一致的。

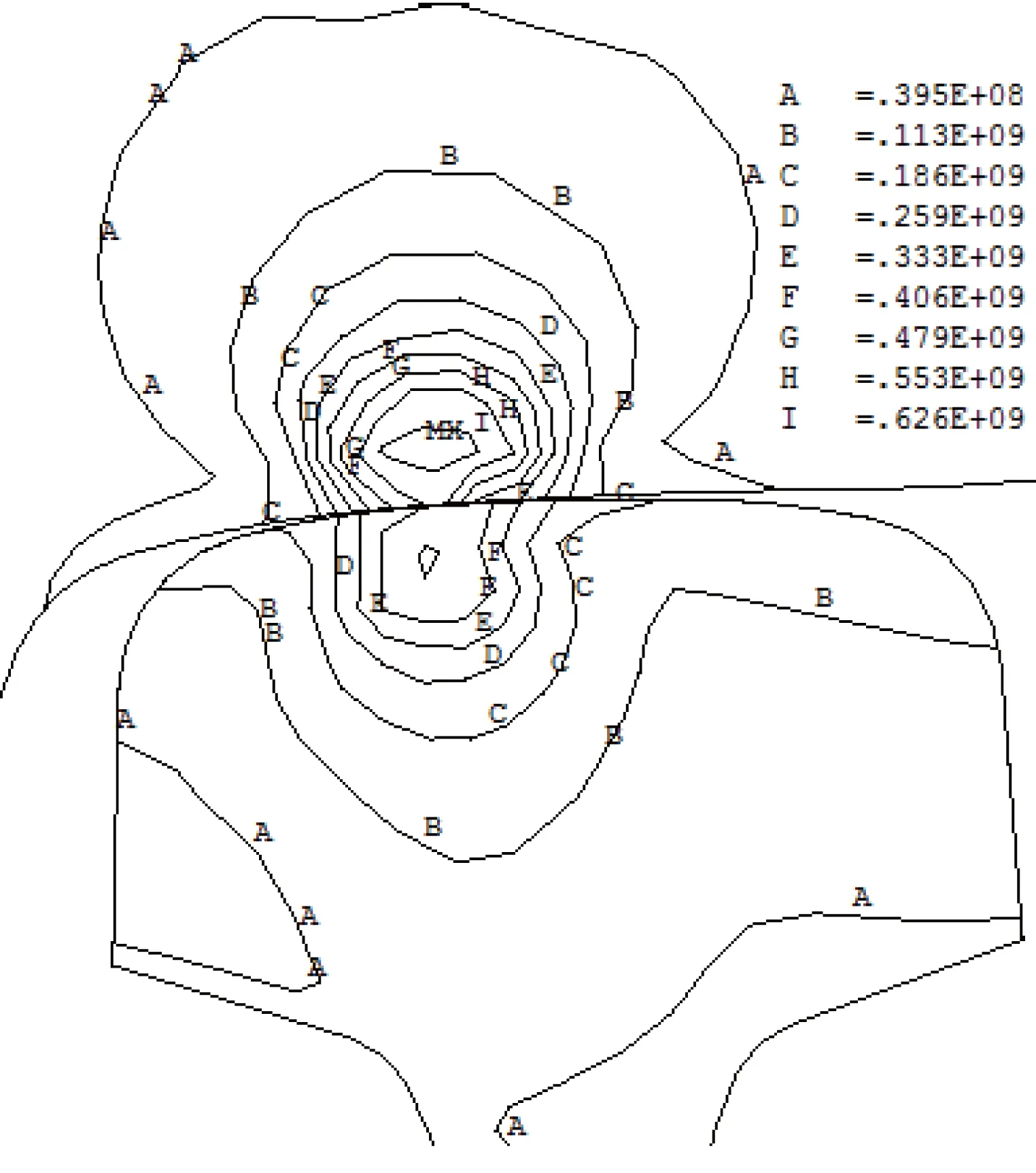
图9 右轮轨接触区域Mises应力等值线

3 结论

本文依据结构分析软件，建立包含一个轮对的三维有限元轮轨接触模型，分析了在地基刚度不变的情况下，轮轨接触特性与轴重的关系，从计算的结果中得到以下结论。

(1)在相同的轮对摇头角和中心横移量下，随着轴重的增加，接触斑的形状不断的发生变化，接触斑的面积也在不断的增大，最大接触斑面积是最小接触斑面积的2.06倍。

(2)列车蛇形运动时，接触斑的形状和位置时刻在发生变化。接触斑形状明显不同于用Hertz理论得到的椭圆形接触斑。轮轨最大的Mises等效应力发生在接触表面的次表层0.5～4.0 mm 的位置处。

(3)轮轨的接触特性受轴重的影响较大，轮对摇头角对接触特性的影响不明显。

[1] 王开云，刘鹏飞.车辆蛇形运动状态下重载铁路轮轨系统振动特性[J].工程力学，2012，29(1)：235-236.

[2] 郭火明，王文健，刘腾飞，等.重载铁路钢轨损伤行为分析[J].中国机械工程，2014，25(2)：267-269.

[3] 刘鹏飞，王开云，翟婉明，等.30 t轴重重载货车轮轨接触几何关系及动态匹配关系[J].重庆理工大学学报：自然科学版，2013，27(9)：22-24.

[4] KUMINEK T，ANIOLEK K . Methodology and verification of calculations for contact stresses in a wheel-rail system[J].Vehicle System Dynamics， 2014，52(1)：111-113.

[5] Wu Fengqi， Zhang Jin， Yao Wenqing. Crane Wheel-Rail Contact Stresses Research Based on Experimental Test and Finite Element Analysis[J]. Applied Mechanics and Materials， 2014，496-500:662-664.

[6] ARSLAN M A，KAYABASL O . 3-D Rail-Wheel contact analysis using FEA[J]. Advances in Engineering Software， 2012(45)：325-329.

[7] 杨丽娟，丁学锋，付昌友，等.澳大利亚某矿区配套铁路重载技术选型研究[J].铁道标准设计，2014，58(1)：45-46.

[8] 孙永路.33 t大轴重机车的动力学特性分析[D].成都：西南交通大学，2013:8-11.

[9] 郭子煜.重载铁路大跨度钢桁梁桥面系选择及分析[J].铁道标准设计，2014，58(3)：90-91.

[10]中华人民共和国铁道部.TB/T 449—2003机车车辆车轮轮缘踏面外形[S].北京：中国铁道出版社，2003.

[11]常崇义.有限元轮轨滚动接触理论及其应用研究[D].北京：中国铁道科学研究院，2010：108.

[12]许贵满，吴亚平，段志东，等.轮轨三维非线性静态接触应力及其影响因素分析[J].兰州交通大学学报，2013，32(4)：68-70.

[13]金学松，刘启月.轮轨摩擦学[M].北京：中国铁道出版社，2004：33-34.

[14]王新敏，李义强，许宏伟.ANSYS结构分析单元与应用[M].北京：人民交通出版社，2011：385-386.

Analysis of Wheel/rail Contact Characteristics in Case of Hunting Motion

WEI Yun-peng1， WU Ya-ping1， DUAN Zhi-dong1， XU Gui-man1， WANG Liang-bi2

(1.School of Civil Engineering， Lanzhou Jiaotong University， Lanzhou 730070， China;2.School of Mechatronic Engineering， Lanzhou Jiaotong University， Lanzhou 730070， China)

To investigate the characteristics of contact shapes， areas， contact stress and Mises stress in wheel/rail contact regions in case of hunting motion， a finite element model of wheel/rail system comprising of two wheelsets is established based on finite element theory and ANSYS. The relationships between contact characteristics and axle loads and wheelset yaw angles are calculated and analyzed. The results show that the effect of wheelset yaw angles on the contact characteristics is not obvious， but the axle loads and wheel center transverse movement have significant effect on the contact areas and shapes， and the contact shapes are different from the elliptic contact shapes obtained by Hertz theory.

Wheel-rail relation; Hunting motion; Contact characteristics; Finite element

2014-06-13；

2014-07-01

国家自然科学基金重点项目(51236003)

魏云鹏(1988—)，男，硕士研究生，E-mail：ypweiinchina@126.com。

1004-2954(2015)03-0037-04

U239.4

A

10.13238/j.issn.1004-2954.2015.03.009