Fractional Action-Like Variational Problem and Its Noether Symmetries for a Nonholonomic System

Zhang Yi（张毅），Long Zixuan（龙梓轩）

1.College of Civil Engineering，Suzhou University of Science and Technology，Suzhou 215011，P.R.China

2.College of Mathematics and Physics，Suzhou University of Science and Technology，Suzhou 215009，P.R.China

Fractional Action-Like Variational Problem and Its Noether Symmetries for a Nonholonomic System

Zhang Yi（张毅）1*，Long Zixuan（龙梓轩）2

1.College of Civil Engineering，Suzhou University of Science and Technology，Suzhou 215011，P.R.China

2.College of Mathematics and Physics，Suzhou University of Science and Technology，Suzhou 215009，P.R.China

Eor an in-depth study on the symmetric properties for nonholonomic non-conservative mechanical systems，the fractional action-like Noether symmetries and conserved quantities for nonholonomic mechanical systems are studied，based on the fractional action-like approach for dynamics modeling proposed by El-Nabulsi.Eirstly，

nonholonomic system；fractional action-like variational problem；symmetric transformation；Noether theorem；conserved quantity

0 Introduction

The fractional calculus has provided a powerful mathematical tool for a great number of problems in different fields of science and engineering，and has made many break-through results in mathematical physics，classical and quantum mechanics，control theory，nonlinear dynamics，signal and image processing，thermodynamics，bioengineering and other fields［1-2］. Although various fields of application of fractional calculus are already well established，some others have just started.The researches in fractional variational problems and their symmetry and conserved quantity are examples of the latter.

The study of fractional variational problems began in the work of Riewe［3-4］.In 1996，Riewe

first applied fractional calculus to a non-conservative mechanics modeling，and the fractional Euler-Lagrange equations and the fractional Hamilton equations were formed initially.Since then，the fractional variational problems have become one of the most popular research areas in applied mathematics，physics，dynamics and control，and are increasingly attracting the attention of many scholars：Klimek［5-6］， Agrawal［7-9］， Atanackovic＇［10-11］，Jumarie［12］，Baleanu［13-15］， Torres［16-18］，El-Nabulsi［19-24］， Cresson［25］， Rabei［26］， Tarasov［27］，and Zhang［28-29］，et al.These scholars came up with a variety of fractional models and methods from different views，and established the corresponding fractional Euler-Lagrange equations and fractional Hamilton equations.Erom the point of view of both classical and quantumsystems，the existence of a number of different fractional variational problems and the need for a more precise description of the fractional model，in part，can be interpreted as the nonlocal nature of fractional order differential operators and the corresponding adjoint operators for describing the dynamics.Another reason is that there exist many different fractional integral operators，including Grünwald-Letnikov，Caputo，Riesz，Riemann-Liouville operators，and so on.The Riemann-Liouville operator is one of the most frequently used in the application of fractional calculus operators.

In order to establish a non-conservative dynamical system model，El-Nabulsi presented a modeling method［19］in 2005，known as the fractional action-like variational approach（also called the El-Nabulsi＇s fractional model）.In his method，the fractional integral about time only needs one parameter，and the resulting fractional Euler-Lagrange equations contain the dissipative forces depending on time.However，there are an arbitrary number of fractional parameters（the order of the derivative）in other fractional models.The novelty of El-Nabulsi dynamics model is that the derived Euler-Lagrange equations are similar to the classical ones，with no fractional derivatives，but the presence of the fractional generalized external force acts on the system.The fractional action-like approach was further extended to the situation of Lagrangian depending on Riemann-Liouville fractional derivatives［20］，to the multi-dimensional fractional action-like variational problems［21］，the fractional action-like variational problems with holonomic constraints or nonholonomic constraints or dissipative dynamic systems［22］，the fractional action-like variational problems with exponential law［23］，and the universal fractional action-like Euler-Lagrange equations from a generalized fractional derivative operator［24］.Erederico and Torres studied the constant of motion for fractional action-like variational problems，gave Noether＇s theorem［30］for nonconservative system under El-Nabulsi＇s fractional model，and extended to the situation of Lagrangian containing higher-order derivatives［31］.Recently，authors have obtained the Noether＇s theorem for Birkhoffian system［32］under El-Nabulsi＇s fractional model，the Noether＇s theorems for Lagrange systems［33］and Hamilton systems［34］based on the extended exponentially fractional integral.

Here the Noether theory for holonomic systems and nonholonomic systems is further studied under the framework of fractional action-like variational approach.The definitions and criteria of fractional action-like Noether symmetric transformations and Noether quasi-symmetric transformations are provided.The fractional action-like Noether theorems of holonomic systems and nonholonomic systems are derived.And the conserved quantities led by the fractional action-like Noether symmetries are given.

1 Fractional Action-Like Variational Problem

Assume that the configuration of a mechanical system is determined by generalized coordinates qk（k = 1，…，n），the Lagrangian of the system is L=L（τ，q，.q）.With the fractional action-like variational approach for modeling of nonconservative dynamical system presented by El-Nabulsi［19］，the fractional variational problem under Riemann-Liouville fractional integrals can be defined as follows.

Eind the stationary points of the integral function

with the fixed boundary conditions

The above variational problem is called the fractional action-like variational problem.Eq.（1）can also be called the fractional action-like Hamilton action.Whenα=1，the problem becomes a classical variational problem of a dynamicalsystem.

According to the theory of calculus of variations，the necessary condition to achieve extreme for Eq.（1）at qk=qk（τ ）is its variation equal to 0，that is，δS=0.Therefore，one can have the following equation

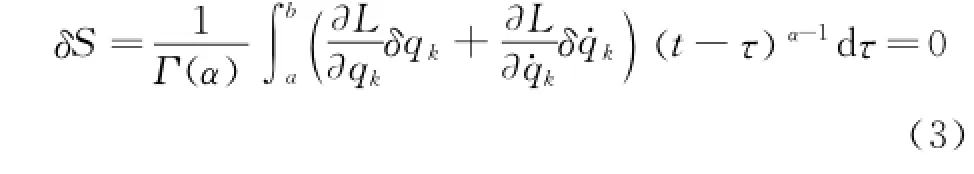
Using the boundary conditions Eq.（2），one has

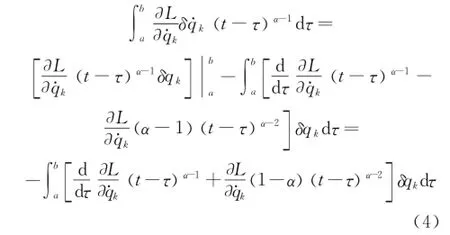
Substituting Eq.（4）into Eq.（3），it becomes

Since the variationsδqk（ k=1，…，n ）are independent of each other for a holonomic system，therefore，by the fundamental lemma［35］of the calculus of variations，one obtains

Erom Eq.（6），one gets

Eq.（7）are the fractional action-like Lagrange equations of the holonomic system［19］.

Assume that the motion of the system is subjected to g bilateral ideal nonholonomic constraints of Chetaev type

The restriction of constraints Eq.（8）exerted on the virtual displacements is

Erom Eq.（5）and the conditions Eq.（9），by using the Lagrange multiplier method，one can obtain

whereλβare the constraint multipliers.Eq.（10）can be called the fractional action-like differential equations of motion with multipliers for the nonholonomic system.

Before integrating the equations of motion，by using Eqs.（8，10），one can findλβas the function of t，q and q·.Therefore，Eqs.（10）can be written in the form

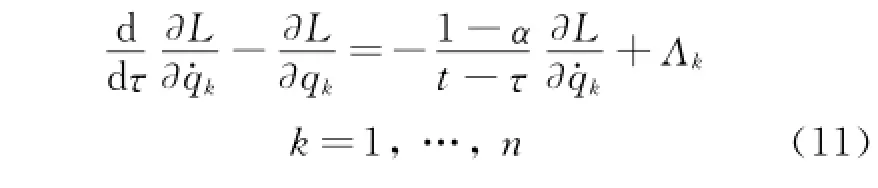
where

Eqs.（11）are called the equations of motion of the holonomic system corresponding to the nonholonomic system，or the equations of motion of the corresponding holonomic system for short.

If the initial conditions satisfy the equations of nonholonomic constraints Eq.（8），the motion of the corresponding holonomic system Eq.（12）will give the solution of the nonholonomic system Eqs.（8，10）.

Example 1 Consider a system whose configuration is determined by two generalized coordinates q1，q2.The Lagrangian of the system is

and its motion is subject to a nonholonomic constraint［36］

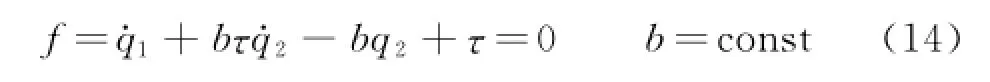
Erom Eqs.（10），one has

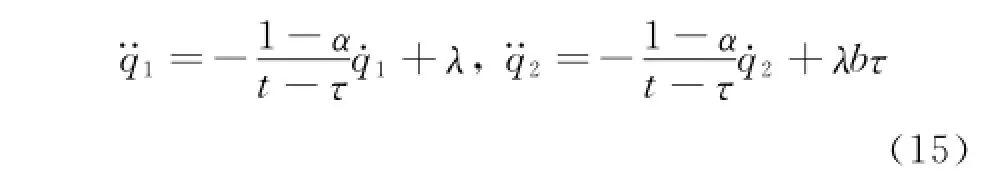
where the first term of the right side of each equation of Eqs.（15）can be viewed as a generalized external force acting on the system，and the second one is the force corresponding to the nonholonomic constraint Eq.（14）.Erom Eqs.（14，15），one can find the multiplier

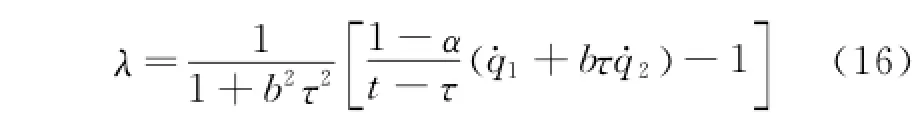
Then Eqs.（15）can be written as

Eqs.（17）are the fractional action-like differential equations of motion of the holonomic system corresponding to the nonholonomic system Eqs.（14，15）.Ifα =1，Eqs.（17）give the equations of motion in classic situation［36］.

2 Variation of Fractional Action-Like Hamilton Action

Introduce the infinitesimal transformations of r-parameters finite transformation group

or their expansion formulae

whereεσ（σ=1，…，r ）are the infinitesimal parameters，andhe generators or generating functions for the infinitesimal transformations.

The difference of the fractional action-like Hamilton action Eq.（1）before and after transformation is

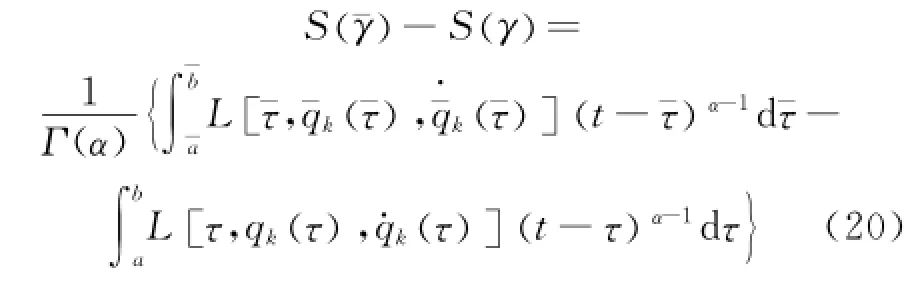
whereγis the given curve andγ-a neighbor curve. Denoting the main linear part of Eq.（20）forεσ，i.e.，the part accurate to the first-order infinitesimal，asΔS，one has

Eor an arbitrary function E，the relation between the non-isochronous variationΔand the isochronous variationδis［36］

Therefore one has

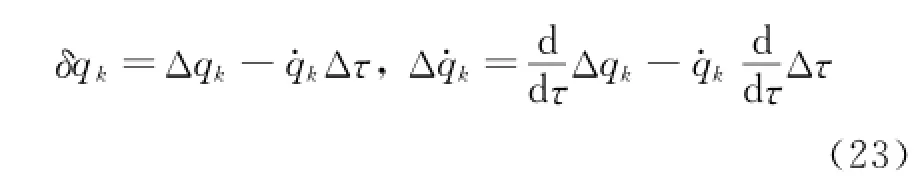
Erom Eq.（23），Eq.（21）can be expressed as

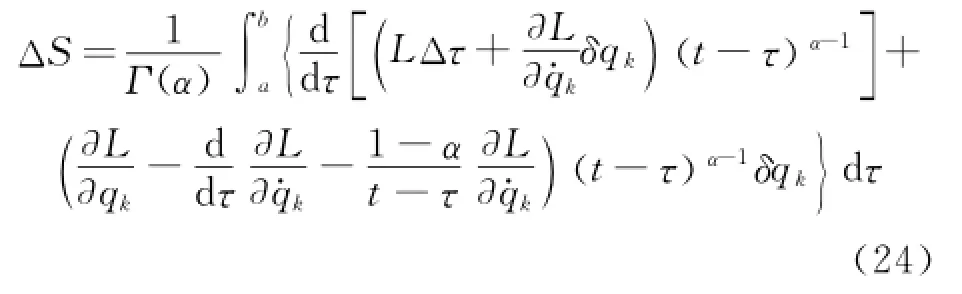
Erom Eqs.（19，23），Eq.（24）can be further expressed as

Eqs.（21，25）are basic formulae for the variation of fractional action-like Hamilton action.

3 Fractional Action-Like Symmetric Transformation

In this section，one establishes the definitions and criteria of fractional action-like Noether symmetric transformations and quasi-symmetric transformations.

Definition 1 If the fractional action-like Hamilton action Eq.（1）is an invariant of the infinitesimal transformations of the group in Eq.（18），that is，for each of the infinitesimal transformations，the formula

ΔS=0 （26）holds，the infinitesimal transformations are called the fractional action-like Noether symmetric transformations.

Erom Definition 1 and Eq.（21），one can obtain the following criterion.

Criterion 1 Eor the infinitesimal transformations of the group in Eq.（18），if the condition

is satisfied，the infinitesimal transformations are the fractional action-like Noether symmetric transformations.

Condition Eq.（27）can also be expressed as

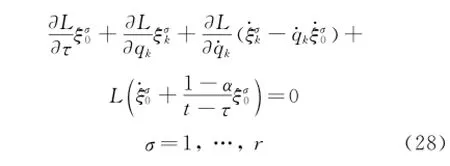
When r=1，Eq.（28）may be called the fractional action-like Noether identity.

Erom Definition 1 and Eq.（25），one can obtain the criterion as follows.

Criterion 2 Eor the infinitesimal transformations of the group in Eq.（19），if the conditions

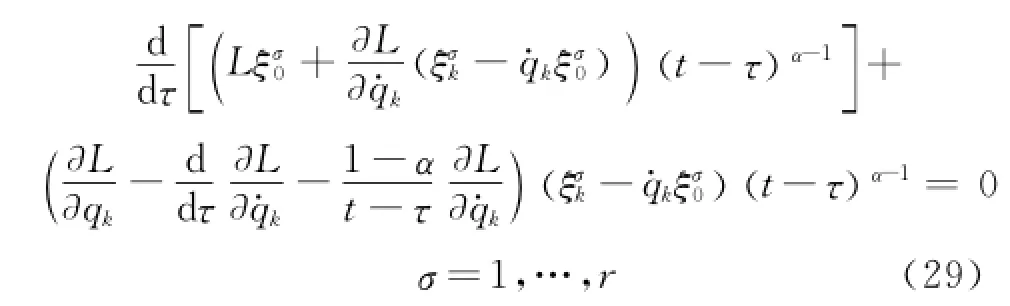
are satisfied，the infinitesimal transformations are the fractional action-like Noether symmetric transformations.

Subsequently，one establishes the definition and criteria of the fractional action-like Noether quasi-symmetry transformations.

Suppose that L＇is another Lagrangian，if the infinitesimal transformations（Eq.（18））accurate to the first-order infinitesimal satisfy the condition

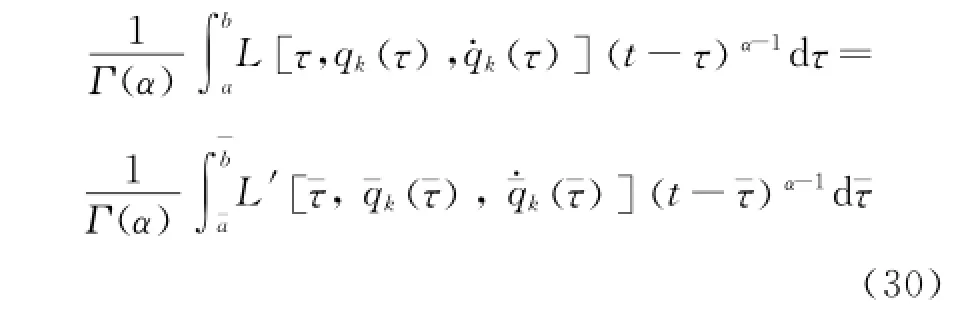
this invariance is called the quasi-invariance of the fractional action-like Hamilton action Eq.（1）under the infinitesimal transformations of the group in Eq.（18）.The functions L＇and L determined by Eq.（30）satisfy the same differential equations of motion.Hence the transformations are called the fractional action-like Noether quasi-symmetric transformations，and one has

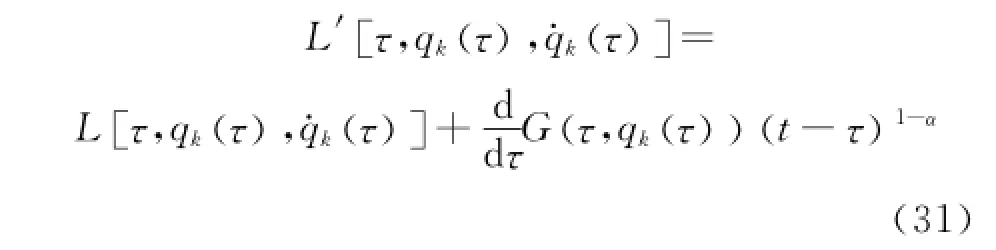
Substituting Eq.（31）into Eq.（30），one has

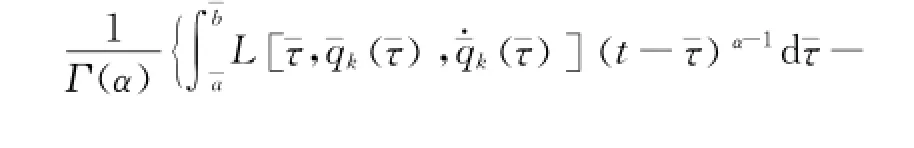
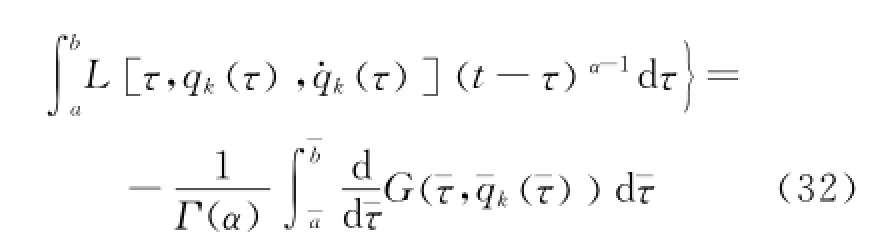
The left-hand of Eq.（32）is a first-order infinitesimal under the transformations （Eq.（18））. Therefore，the right-hand should be an infinitesimal of the same-order.G can be replaced byΔG，and thus

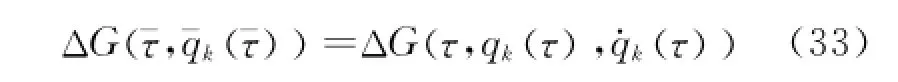
Hence，one has

Definition 2 If the fractional action-like Hamilton action Eq.（1）is a quasi-invariant under the infinitesimal transformations of group （18），i.e.for each of the infinitesimal transformations，the formula

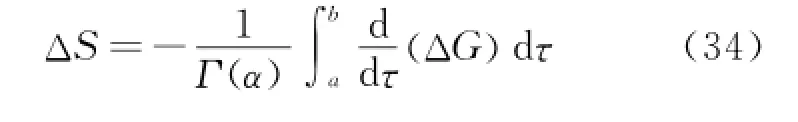
holds，where G =G（τ，q，q·），the infinitesimal transformations are called the fractional actionlike Noether quasi-symmetric transformations.

Erom Definition 2 and Eq.（25），one can get the following criterion.

Criterion 3 Eor the infinitesimal transformations of group（18），if the condition

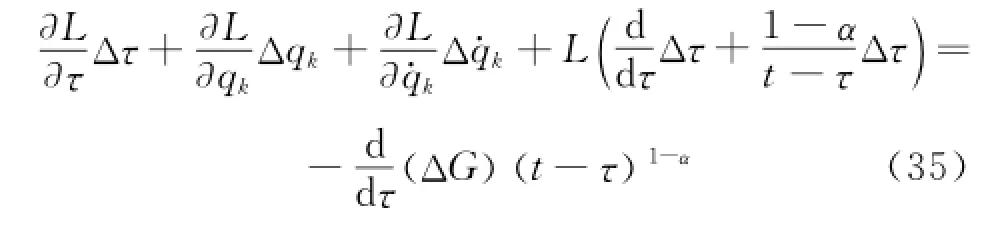
is satisfied，the infinitesimal transformations are the fractional action-like Noether quasi-symmetric transformations.

Condition Eq.（35）can also be expressed as

Erom Definition 2 and Eq.（25），one can suggest the criterion as follows

Criterion 4 Eor the infinitesimal transformations of the group in Eq.（19），if the conditions

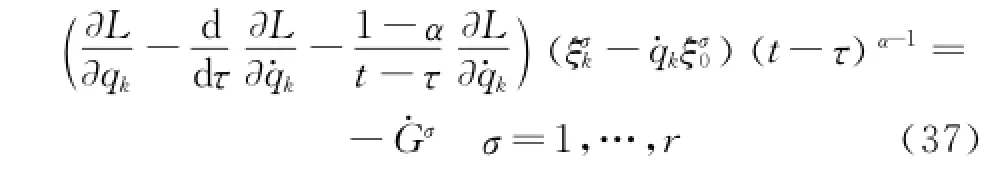
are satisfied，the infinitesimal transformations are the fractional action-like Noether quasi-symmetric transformations.

By using Criterions 1，2，one can determine the fractional action-like Noether symmetry. Likewise，by using Criterions 3，4，one can define the fractional action-like Noether quasi-symmetry.

4 Fractional Action-Like Noether Theorem of Holonomic System

The conserved quantity of a holonomic system under the El-Nabulsi＇s fractional model is firstly defined.

Definition 3 A function I（τ，q，q·）is said to be a conserved quantity of a holonomic system under El-Nabulsi＇s fractional model if

is along all the solution curves of the fractional action-like Lagrange equations.（7）.

Eor a holonomic system，if one can find a fractional action-like Noether symmetric transformation or a Noether quasi-symmetric transformation，one can find a corresponding conserved quantity.Here is the obtained theorem.

Theorem 1 Eor the holonomic system Eq.（7），if the infinitesimal transformations of group Eq.（19）are the fractional action-like Noether symmetric transformations under Definition 1，the system has r linear and independent conserved quantities，that is

Proof Since the infinitesimal transformations of group are the fractional action-like Noether symmetric transformations of the system.By Definition 1，one hasΔS=0，namely

Substituting Eq.（7）into Eq.（40），and considering the independence of parametersεσ，one has

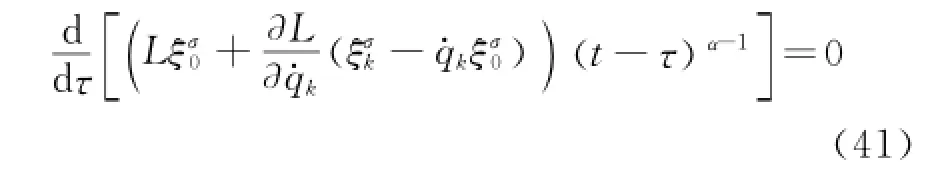
Integrating it，Eq.（39）is obtained，and then it ends.

Theorem 2 Eor the holonomic system Eq.（7），if the infinitesimal transformations of the group in Eq.（19）are the fractional action-like Noether quasi-symmetric transformations under Definition 2，the system exists r linear independent conservation quantities，such as

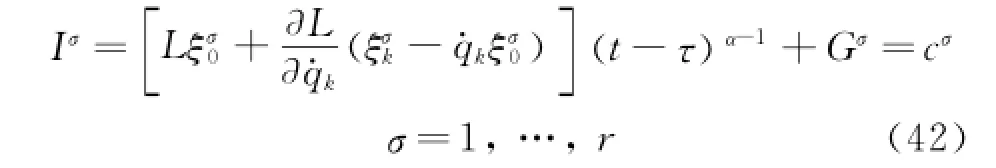
Theorems 1，2 can be called the fractional action-like Noether theorem for the holonomic system.According to the Noether theorem，for the holonomic system under El-Nabulsi＇s fractional model，if one can find a fractional actionlike Noether symmetric transformation or a quasisymmetric transformation，one can get a conserved quantity of the system.

Example 2 The Lagrangian of the planar Kepler problem is

Here one tries to study the fractional action-like Noether symmetries and conserved quantities of the system.

Eirst，one finds the fractional action-like Noether quasi-symmetric transformations.Eractional action-like generalized Noether identity Eq.（36）gives

Eq.（44）has the following solutions

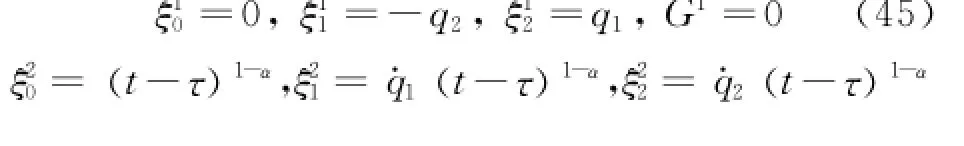
Eq.（47）is a conserved quantity led by the fractional action-like Noether symmetry Eq.（45）of the system.Whenα=1，Eq.（47）gives

This is the conserved quantity of a classical Kepler problem［36］.

Erom the generator Eq.（46），according to Theorem 2，one obtains

Therefore，the infinitesimal transformation corresponding to the generator Eq.（46）is trivial.

The generator Eq.（45）is corresponding to a fractional action-like Noether symmetric transformation of the system，and the generator Eq.（46）is corresponding to a fractional action-like Noether quasi-symmetric transformation of the system.

Erom the generator Eq.（45），according to Theorem 1，one has

5 Fractional Action-Like Noether Theorem of Nonholonomic System

The definition of fractional action-like Noether quasi-symmetric transformations of the nonholonomic system is firstly given.

Notice that

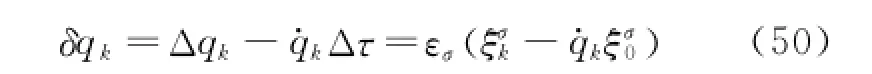
Substituting Eq.（50）into Eq.（9），and considering the independence ofεσ，one has

This is the restriction of nonholonomic constraints exerted on the generating function of infinitesimal transformations，called the Appell-Chetaev conditions.Thus one has

Definition 4 Eor the nonholonomic system Eqs.（8，10），if the infinitesimal transformations of the group in Eq.（19）are the fractional actionlike Noether quasi-symmetric transformations，satisfying the Appell-Chetaev conditions Eq.（51），the transformations are called the fractional action-like Noether quasi-symmetric transformations of the nonholonomic system.

Secondly，one gives the definition of a conserved quantity of a nonholonomic system under El-Nabulsi＇s fractional model.

Definition 5 A function I（τ，q，q·）is said to be a conserved quantity of a nonholonomic system under El-Nabulsi＇s fractional model if

is along all the solution curves of the fractional action-like differential equations of motion of the nonholonomic system Eqs.（8，10）.

Einally，one establishes the fractional actionlike Noether theorem of the nonholonomic system.

Theorem 3 Eor the nonholonomic system Eqs.（8，10），if the infinitesimal transformations of the group in Eq.（19）are the Noether quasisymmetric transformations under Definition 4，the system has r linear independent conserved quantities

Proof Since the infinitesimal transformations of group are the fractional action-like Noether quasi-symmetric transformations of the system，by Definition 2，one has

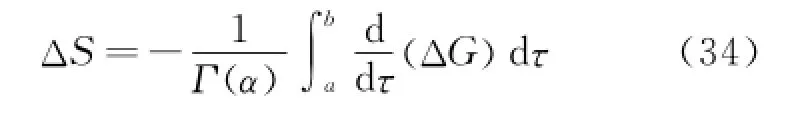
Eq.（34）can also be written as

Since the infinitesimal transformations satisfy the Appell-Chetaev conditions Eq.（51），one has

Adding Eq.（55）and Eq.（54）together，one gets

Substituting Eq.（10）into Eq.（56），and considering the independence ofεσ，one obtains

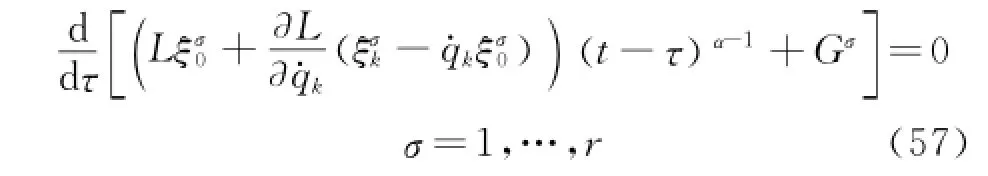
Integrating it，one obtains Eq.（53），and the theorem is thus proved.

Theorem 3 can be called the fractional actionlike Noether theorem of the nonholonomic system.By the theorem，one can find a conserved quantity from a known Noether symmetry.

If the nonholonomic constraints do not exist，then Theorem 3 degenerates to Theorem 2，and if at the same time Gσ=0 is satisfied，Theorem 3 degenerates to Theorem 1.

Example 3 Let us study the fractional action-like Noether symmetries and the conserved quantities of the nonholonomic system discussed in Example 1.

Eirst，one tries to find the fractional actionlike Noether quasi-symmetric transformations satisfying the Appell-Chetaev conditions.The fractional action-like generalized Noether identity Eq.（36）gives

and the Appell-Chetaev conditions Eq.（51）give

Eqs.（58，59）have the following solutions

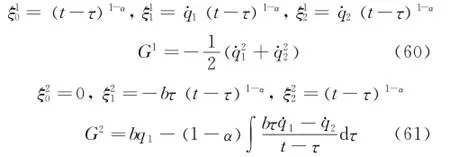
The generators Eqs.（60，61）are both corresponding to the fractional action-like Noether quasi-symmetric transformation of the nonholonomic system.By Theorem 3，the conserved quantity Eq.（53）gives

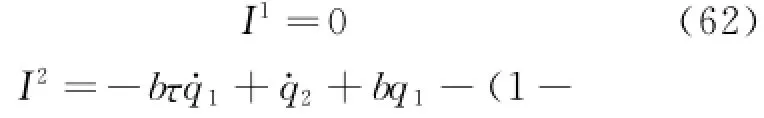
Therefore，the infinitesimal transformation corresponding to the generator Eq.（60）is trivial.And whenα=1，the conserved quantity Eq.（63）gives

This is a classical conserved quantity［36］.

6 Conclusions

In recent decades，the fractional calculus has been successfully used in various fields of science and engineering.It has also been used in dynamics modeling for a non-conservative or dissipative system and so on，where some complex problems can be solved difficultly with integer order derivatives.Here the fractional action-like variational problem is further studied，based upon the fractional modeling presented by El-Nabulsi.The fractional action-like differential equations of motion for both holonomic and nonholonomic systems are established.The definitions and criteria of both fractional action-like Noether symmetric transformations and Noether quasi-symmetric transformations are given，and the fractional action-like Noether theorems of the systems are established.The presented methods and its results are of universal significance.They can be further applied to various types of constrained mechanical systems.It is noteworthy that classical Noether theory for the circumstance of integer order is a special case of this paper.

Acknowledgement

This work was supported by the National Natural Science Eoundation of China（No.11272227）.

［1］ Podlubny I.Eractional differential equations ［M］. San Diego：Academic Press，1999.

［2］ Herrmann R.Eractional calculus：An introduction for physicists［M］.Singapore：World Scientific，2011.

［3］ Riewe E.Nonconservative Lagrangian and Hamiltonian mechanics ［J］.Physical Review E，1996，53（2）：1890-1899.

［4］ Riewe E.Mechanics with fractional derivatives［J］. Physical Review E，1997，55（3）：3581-3592.

［5］ Klimek M.Eractional sequential mechanics-modelswith symmetric fractional derivative［J］.Czechoslovak Journal of Physics，2001，51（12）：1348-1354.

［6］ Klimek M.Lagrangian and Hamiltonian fractional sequential mechanics ［J］.Czechoslovak Journal of Physics，2002，52（11）：1247-1253.

［7］ Agrawal O P.Eormulation of Euler-Lagrange equations for fractional variational problems［J］.Journal of Mathematical Analysis and Applications，2002，272（1）：368-379.

［8］ Agrawal O P.Generalized Euler-Lagrange equations and transversality conditions for EVPs in terms of the Caputo derivative［J］.Journal of Vibration and Control，2007，13（9/10）：1217-1237.

［9］ Agrawal O P，Muslih S I，Baleanu D.Generalized variational calculus in terms of multi-parameters fractional derivatives［J］.Communications in Nonlinear Science and Numerical Simulation，2011，16（12）：4756-4767.

［10］Atanackovic＇T M，Konjik S，Pilipovic＇S.Variational problems with fractional derivatives：Euler-Lagrange equations［J］.Journal of Physics A：Mathematical and Theoretical，2008，41（9）：095201.

［11］Atanackovic＇T M，Konjik S，Pilipovic＇S，et al.Variational problems with fractional derivatives：Invariance conditions and Noether＇s theorem ［J］.Nonlinear Analysis：Theory， Methods & Applications，2009，71（5/6）：1504-1517.

［12］Jumarie G.Eractional Hamilton-Jacobi equation for the optimal control of nonrandom fractional dynamics with fractional cost functions［J］.Journal of Applied Mathematics and Computing，2007，23（1/2）：215-228.

［13］Baleanu D，Avkar T.Lagrangians with linear velocities within Riemann-Liouville fractional derivatives［J］.Nuovo Cimento B，2003，119（1）：73-79.

［14］Baleanu D，Trujillo J I.A new method of finding the fractional Euler-Lagrange and Hamilton equations within Caputo fractional derivatives［J］.Communications in Nonlinear Science and Numerical Simulation，2010，15（5）：1111-1115.

［15］Baleanu D，Muslih S I，Rabei E M，et al.On fractional Hamiltonian systems possessing first-class constraints within Caputo derivatives［J］.Romanian Reports in Physics，2011，63（1）：3-8.

［16］Almeida R，Torres D E M.Necessary and sufficient conditions for the fractional calculus of variations with Caputo derivatives ［J］.Communications in Nonlinear Science and Numerical Simulation，2011，16（3）：1490-1500.

［17］Odzijewicz T，Malinowska A B，Torres D E M. Eractional variational calculus with classical and combined Caputo derivatives ［J］.Nonlinear Analysis：Theory，Methods & Applications，2012，75（3），1507-1515.

［18］Malinowska A B，Torres D E M.Generalized natural boundary conditions for fractional variational problems in terms of the Caputo derivative［J］.Computers and Mathematics with Applications，2010，59（9）：3110-3116.

［19］El-Nabulsi A R.A fractional approach to nonconservative Lagrangian dynamical systems［J］.Eizika A，2005，14（4）：289-298.

［20］El-Nabulsi A R.Necessary optimality conditions for fractional action-like integrals of variational calculus with Riemann-Liouville derivatives of order （α，β）［J］.Mathematical Models & Methods in Applied Sciences，2007，30（15）：1931-1939.

［21］El-Nabulsi A R，Torres D E M.Eractional actionlike variational problems［J］.Journal of Mathematical Physics，2008，49（5）：053521.

［22］El-Nabulsi A R.Eractional action-like variational problems in holonomic，non-holonomic and semi-holonomic constrained and dissipative dynamical systems［J］.Chaos，Solitons and Eractals，2009，42（1）：52-61.

［23］El-Nabulsi A R.Eractional variational problems from extended exponentially fractional integral［J］.Applied Mathematics and Computation，2011，217（22）：9492-9496.

［24］El-Nabulsi R A.Universal fractional Euler-Lagrange equation from a generalized fractional derivate operator［J］.Central European Journal of Physics，2011，9（1）：250-256.

［25］Cresson J.Eractional embedding of differential operators and Lagrangian systems［J］.Journal of Mathematical Physics，2007，48（3）：033504.

［26］Rabei E M，Rawashdeh I M，Muslih S，et al.Hamilton-Jacobi formulation for systems in terms of Riesz＇s fractional derivatives［J］.International Journal of Theoretical Physics，2011，50（5）：1569-1576.

［27］Tarasov V E.Eractional dynamics［M］.Beijing：Higher Education Press，2010.

［28］Zhou Y，Zhang Y.Eractional Pfaff-Birkhoff principle and Birkhoff＇s equations in terms of Riesz fractional derivatives［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2014，31（1）：63-69.

［29］Zhou Y，Zhang Y.Noether＇s theorems of a fractional Birkhoffian system within Riemann-Liouville deriva-tives ［J］.Chinese Physics B，2014，23（12）：124502.

［30］Erederico G SE，Torres D E M.Constants of motion for fractional action-like variational problems［J］.International Journal of Applied Mathematics，2006，19（1）：97-104.

［31］Erederico G S E，Torres D E M.Non-conservative Noether＇s theorem for fractional action-like problems with intrinsic and observer times［J］.International Journal of Ecological Economics&Statistics，2007，9（E07）：74-82.

［32］Zhang Y，Zhou Y.Symmetries and conserved quantities for fractional action-like Pfaffian variational problems［J］.Nonlinear Dynamics，2013，73（1-2）：783-793.

［33］Long Z X，Zhang Y.Eractional Noether theorem based on extended exponentially fractional integral［J］.International Journal of Theoretical Physics，2014，53（3）：841-855.

［34］Long Z X，Zhang Y.Noether＇s theorem for fractional variational problem from El-Nabulsi extended exponentially fractional integral in phase space［J］.Acta Mechanica，2014，225（1）：77-90.

［35］Goldstein H，Poole C，Safko J.Classical Mechanics［M］.Third Edition.Beijing：Higher Education Press，2005.

［36］Mei E X ，Wu H B.Dynamics of constrained mechanical systems［M］.Beijing：Beijing Institute of Technology Press，2009.

（Executive editor：Zhang Tong）

O316 Document code：A Article ID：1005-1120（2015）04-0380-10

*Corresponding author：Zhang Yi，Professor，E-mail：zhy@mail.usts.edu.cn.

How to cite this article：Zhang Yi，Long Zixuan.Eractional action-like variational problem and its Noether symmetries for a nonholonomic system［J］.Trans.Nanjing U.Aero.Astro.，2015，32（4）：380-389.

http：//dx.doi.org/10.16356/j.1005-1120.2015.04.380

（Received 14 August 2014；revised 5 December 2014；accepted 14 December 2014）

the fractional action-like variational problem is established，and the fractional action-like Lagrange equations of holonomic system and the fractional action-like differential equations of motion with multiplier for nonholonomic system are given；secondly，according to the invariance of fractional action-like Hamilton action under infinitesimal transformations of group，the definitions and criteria of fractional action-like Noether symmetric transformations and quasi-symmetric transformations are put forward；finally，the fractional action-like Noether theorems for both holonomic system and nonholonomic system are established，and the relationship between the fractional action-like Noether symmetry and the conserved quantity is given.