Resolution Increase and Noise Removal in Particle Size Distribution Measurement with Shifrin Transform

Han Yue（韩月），Yang Zongling（杨宗苓），Qiao Xing（乔星），Qian Peng（钱鹏），Yuan Yinnan（袁银男），Ding Sihong（丁思红），Dai Bing（戴兵），*

1.School of Sciences，Nantong University，Nantong 226019，P.R.China；

2.School of Mechanical Engineering，Nantong University，Nantong 226019，P.R.China；

3.School of Geography，Nantong University，Nantong 226019，P.R.China

Resolution Increase and Noise Removal in Particle Size Distribution Measurement with Shifrin Transform

Han Yue（韩月）1，Yang Zongling（杨宗苓）2，Qiao Xing（乔星）2，Qian Peng（钱鹏）3，Yuan Yinnan（袁银男）2，Ding Sihong（丁思红）2，Dai Bing（戴兵）1，2*

1.School of Sciences，Nantong University，Nantong 226019，P.R.China；

2.School of Mechanical Engineering，Nantong University，Nantong 226019，P.R.China；

3.School of Geography，Nantong University，Nantong 226019，P.R.China

Based on the laser diffraction and Shifrin transform，the measurement method of particle size distribution has been improved extensively.While in real measurements，some noise peaks exist in the inversion data and are easily to be misread as particle distribution peaks.The improved method used a truncation function as a filter is hard to distinguish adjacent peaks.Here，by introducing the bimodal resolution criterion，the filter function is optimized，and to a quasi truncation function with the optimized filter function is studied to achieve optimal bimodal resolution and to remove noise peaks.This new quasi truncation function fits multimode distribution very well.By combining the quasi truncation function with Shifrin transform，noise peaks are removed well and the adjacent peaks are distinguished clearly.Finally，laser diffraction experiments are conducted and the particle size distribution is analyzed by adoping the method.The results show that the quasi truncation function has better bimodal resolution than the truncation function.Generally，by combining the quasi truncation function with the Shifrin transform，in particle size distribution measurements with laser diffraction，the bimodal resolution is greatly increased and the noise is removed well.And the results can restore the original distribution perfectly.Therefore，the new method with combination of the quasi truncation function and the Shifrin transform provides a feasible and effective way to measure the multimode particle size distribution by laser diffraction.

diffraction；particle size distribution；Shifrin transform；quasi truncation function；inversion

0 Introduction

In the measurement of particle size distribution（PSD），the optical method has been widely used because of its non-contact and quick testing characteristics［1-7］.Single particle and group particles testing techniques，represented by Coulter counter and Malvern particle analyzer，respectively，have been developed well.At the end of the last century，with the development of charge-coupled device（CCD）components，a method for PSD measurement based on Shifrin transform and laser diffraction was also developed quickly［8-12］. The method has a high precision and the users do not require knowledge of the information in advance，such as the distribution model［7，8，10，11］. However，it has a significant defect［8，9，11，12］，that is，in actual measurements noise in the data of inversion can easily be misread as PSD peaks，thus preventing it from wide application.Recently，one has proposed a few filters that involved inserting a truncation function to avoid misreading noise peaks［12-13］.However，in the experiments，the bimodal resolution was low because of the adjacent peak overlap effect.In order to remove the noise peaks and increase its bimodal resolution，a quasi truncation function with an optimized filter function is proposed in this paper to increase thebimodal resolution.And then the quasi truncation function is combined with Shifrin transform to solve the problems of noise and adjacent peak overlap.This method specifies an effective way to use Shifrin transform and laser diffraction for obtaining multimode PSD.

1 Shifrin Transform Inversion and CTF Method

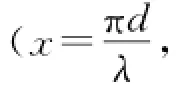
where k is the wave number，F the focal length，θ the scattering angle，and J1the first level of the Bessel function of the first kind.And f（）x is the distribution function，as a function of particle size.Chin and Shifrin［8，10，11］obtained the analytic solution of the inverse problem as

where（）n x is the distribution of particle quality as a function of size，and Y1the first level of the Bessel function of the second kind.Eq.（2）is called the Shifrin transform，which can invert the PSD using the angle distribution of the light scattering intensity.

Many previous reports［6，10-12］have showed that the actual range of sampling angles needs to be fromθmintoθmaxin Eq.（2）.Therefore，data loss is inevitable in actual sampling.The loss of data brings some noise，which can be easily misread as distribution peaks.In fact，this phenomenon becomes a fatal flaw of Shifrin method in the extended application quickly.Consequently，Dai et al.［12，13］proposed a complete truncation function（CTF）based on some characteristics of Fourier transform to improve the Shifrin method. The filter function is defined as

whereβis an adjustable coefficient in a range of 1.5 to 2.0.In some experimental measurements［12，13］，the method can remove noise，and be perfect to restore the original distribution.While，when two of the peaks are closed，serious problems will be encountered.Fig.1 shows the simulation inversion of PSD with three peaks using the CTF and Shifrin methods，respectively.Here，（）n x is the ratio of the particle quality with size parameter x and the total particle quality with all sizes（the same as below），and defined as a positive value according to its physics significance（the same as below）.In its original distribution，particle sizes at three peaks are 25.0，32.0，50.0μm，respectively，and the sampling angles are assumed to be within a range of 0.1°to 5.0°（Figs.2，3）. Due to the data collecting difficultly below 0.1°，the minimum of the sampling angle is selected as 0.1°and，due to the approximate requirements of Fraunhofer diffraction，the maximum of the sampling angle is selected as 5.0°.From Fig.1，it is observed that the noises in inversion for the Shifrin method are much larger than the CTF method.Especially，the noise peak at 42μm is easily misread as distribution peak.For the CTF method，the noises in inversion nearly disappear.But it causes another problem that the two peaks at 25.0 and 32.0μm in the original distribution overlap seriously.These two closed peaks become indistinguishable in the CTF method.It is fatal for restoring the original distribution.

2 New Method

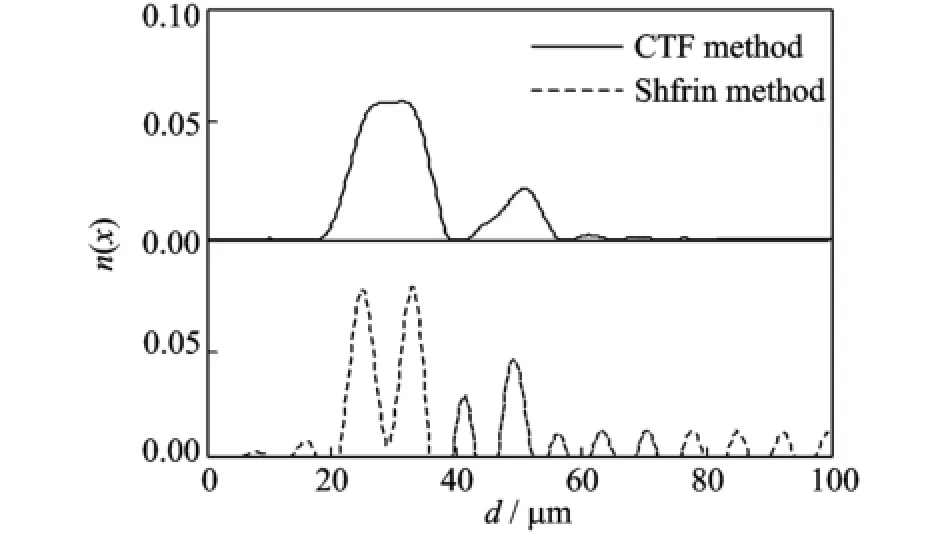
Fig.1 Simulation inversion of PSD with three peaks using CTF and Shifrin methods

To restore the original distribution well，the measurement results needs to be with small noise，high resolution，and high accuracy.Refs.［8-12］have pointed out that the Shifrin method has high measurement precision yet with serious noises；while the CTF method has low noise，but low neighbor peak resolution.Therefore，an optimal filter function or the other methods to meet the requirements of both noise removal and high resolution are presented in the following section.

2.1 A quasi truncation function

For obtaining the optimal filter function，based on the difference in the between theoretical light intensity with the light intensity inversed by the above bad result，then fitted the difference curve，and adjusted the truncation performance of filter function，a quasi truncation function is found out，which has a better neighbor peak resolution than the complete truncation function and the other filter function.The quasi complete truncation function（QCTF）is selected as

Fig.2 is the simulation inversion of PSD with five peaks using the Shifrin method，CTF method and QCTF method.Peak particle sizes are 20.0，26.5，40.0，47.0，65.0μm，respectively.From Fig.2，and according to the bimodal resolution criteria，the neighbor peaks at 20.0 and 26.5μm，as well the ones at 40.0 and 47.0μm，cannot be distinguished for the CTF method，while for the QCTF method，they can be distinguished.Thus，the QCTF method has higher bimodal resolution than the CTF method.At the same time，the QCTF method，as well as the CTF method，has better noise removal than the Shifrin method，as shown in Fig.2.

Fig.2 Simulation inversion of PSD with five peaks using QCTF，CTF and Shifrin method

A lot of simulation experiments have indicated that the QCTF method has high bimodal resolution，and it is suitable to simulate single，bimodal and multimodal particle distribution.However，the QCTF method can reluctantly distinguish the two peaks at 20.0 and 26.5μm in Fig.2. That is to say，on the basis of noise removal，even the optimal filter function method is difficult to solve fundamentally the adjacent peak overlapping problem.The original reason is that，besides the characteristics of the noise removal，the optimal filter function method stretches the peak width，which declines the bimodal resolution.

2.2 Method of combination quasi truncation function with Shifrin transform

In Figs.1，2，the Shifrin method has the narrowest peak width than other methods.Then，a method of combination the quasi truncation func-tion with the Shifrin transform is proposed here to obtain better noise removal and narrower peak width.Firstly，the QCTF method is applied to do the inversion.Then the inversion interval is redistricted according to the inversion results.After that，the Shifrin method is applied for those intervals with particle distribution peaks，and the QCTF method is applied for the other intervals. Fig.3 shows the simulation inversion of PSD with six peaks using the CTF method，the QCTF method and the proposed method.The peak particle sizes are 15.0，23.0，45.0，51.5，70.0，75.0μm，respectively.According to the QCTF inversion results，the new method is redistricted in the interval of 0.0—100.0μm.And the Shifrin method is applied for three intervals of 12.0—25.0μm，42.0—53.0μm，and 68.0—78.0μm. The QCTF method is applied to the other intervals.

Fig.3 Simulation inversion of PSD with six peaks using CTF method，QCTF method and the proposed method

As seen from Fig.3，although the CTF method can remove noises，it is almost unable to restore the original PSD because of the adjacent peak overlap effect.Two peaks at 45.0μm and 51.5μm，as well as the ones at 70.0μm and 75.0 μm，cannot be distinguished.On the other hand，the bimodal resolution of the QCTF method is better than that of the CTF method，while the two peaks at 70.0 and 75.0μm still cannot be distinguished.The method combined the QCTF and Shifrin transform greatly increases the bimodal resolution.In Fig.3，it shows clearly that the six PSD peaks are separated well and，there is almost no noise on the curve.Thus，the current method combined the QCTF and Shifrin transform can perfectly solve both the noise obstacle and the adjacent peak overlap effect.

3 Experiment

3.1 Experimental equipment

As shown in Fig.4，the optical particle-sizing instrument used in this study is mainly composed of a He-Ne laser，an attenuation system，an extended filtering collimation system，a sample box，a lens，a wedge-shaped baffle，a line array CCD，a probe circuit，a data acquisition card，and a computer system.The standard particle latex spheres are provided by the Nuclear Industry Beijing Institute of Chemical Engineering.

Fig.4 Schematic diagram of optical particle-sizing instrument

The particles labeled GBW（E）120006（nominal peak size is 20.46±0.4μm），GBW（E）120042（nominal peak size is 27.10±1.3μm）and GBW（E）120045（nominal peak size is 45.60± 1.3μm）are suspended in pure water，and then the mixture of PSD with three peaks is formed. The particles labeled GBW（E）120046（nominal peak size is 51.20±0.6μm）are dropped into the above suspension，and then the mixture of PSD with four peaks is formed.By adjusting the attenuation system，the scattered light intensity distribution on the CCD is properly obtained，and the obtained signal is converted to an electric signal. The model of the Linear CCD is TCD103C（Toshiba）with 2 592 pixels and the size of a pixel is 11.0μm.In order to reduce the influence of the central spot，it is blocked by a wedge-shaped baffle.

3.2 Results and discussion

Fig.5 is the results of PSD measured by various techniques，including the current method，QCTF method，CTF method，and Shifrin method，for the mixture of GBW（E）120006，GBW（E）120042，and GBW（E）120045.Fig.6 is the results of PSD measured by various techniques for the mixture of GBW（E）120006，GBW（E）120042，GBW（E）120045 and GBW（E）120046. Here，the laser wavelength is 632.8 nm，the focal length of the objective lens is 300 mm.Then，the angle interval can be calculated as 4.00.The sampling angle A（θ）andθmaxare 0.300 4°and 4.794 1°， respectively，and the total number of pixels is 2 140.Mean value of three tests is taken as the light intensity distribution result.When the current method is used to measure PSD with three peaks，according to the results of QCTF method，the Shifrin method is applied for 17.0—30.0μm and 42.0—48.0μm intervals，and the QCTF method is applied for the other intervals.When PSD with four peaks is measured，the Shifrin method is applied for 17.0—30.0μm and 42.0—53.0μm intervals，and the QCTF method is applied for the other intervals.

In Figs.5，6，results of the Shifrin method bring many noise peaks，while results of the CTF method result in serious adjacent peak overlap effect.Therefore，they cannot restore their original PSD.Results of the QCTF method not only remove the noises，but also have certain bimodal resolution.The neighbor peaks formed by GBW（E）120006 and GBW（E）120042 are separated by the QCTF method（Figs.5，6）.While the adjacent peaks formed by GBW（E）120045 and GBW（E）120046 are not distinguished by the QCTF method（Fig.6）.On the other hand，the method with combination of the QCTF with Shifrin transform can clearly show all peaks of the original distribution on the basis of noise removal.As shown in Figs.5，6，peak particle sizes are measured to be 20.3，27.4，45.7，51.5μm，respectively，which agrees with the nominal sizes of the samples.Hence，analyzed the above results，the current method has high bimodal resolution and good effect on the noise removal.The method with the combination of the QCTF and the Shifrin transform can be widely applied to the PSD measurement of group particles by laser diffraction.

Fig.5 PSD obtained by various techniques for mixture of GBW（E）120006，GBW（E）120042 and GBW（E）120045

Fig.6 PSD obtained by various techniques for mixture of GBW（E）120006，GBW（E）120042，GBW（E）120045 and GBW（E）120046

4 Conclusions

（1）The method of quasi truncation function has good bimodal resolution on the basis of noise removal，and it is an optimal selection to directly invert PSD by the analytic method.However，the bimodal resolution is limited by stretched peak width characteristic of the quasi truncation function.

（2）A method combined the quasi truncation function with the Shifrin transform is proposed. The method has a good effect of noise removal with high bimodal resolution，which is favorable to restore the original PSD.

（3）The current method fundamentally improves the inversion method based on the Shifrin transform，and provides a feasible and effectiveapproach to measure actual PSD by laser diffraction.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China（No.51376095）and the Jiangsu Province Environmental Research Projects（No. 2014049）.We gratefully acknowledge the help of Prof. Xiangdong Luo，who gave a lot of advisers in our work and English polishing.

［1］ Zhang Z W，Zhen G，Yu X H，et al.A Novel Laser Natural Size Analyzer within Fraunhofer Diffraction Used to Measure Intermittent Sprays［J］.Chinese Journal of Lasers，1995，22（10）：743-746.（in Chinese）

［2］ Carter R M，Yan Y，Lee P.On-line nonintrusive measurement of particle size distribution through digital imaging［J］.IEEE Transactions on Instrumentation and Measurement，2006，55（6）：2034-2038.

［3］ Lei G，Shao K R，Li Y B，et al.Bayesian inversion method and its information determination for the estimation of particle size distribution in ferrofluids［J］. IEEE Transactions on Magnetics，2009，45（10）：3981-3988.

［4］ Mroczka J，Szczuczyński D.Simulation research on improved regularized solution of the inverse problem in spectral extinction measurements［J］.Appl Opt，2012，51（11）：1715-1723.

［5］ Tang H，Liang G W.Inversion of particle size distribution from spectral extinction data using the bimodal Johnson＇s SB function［J］.Powder Technology，2010（198）：330-336.

［6］ Heekyu Choia，Woong Leea，Seongsoo Kimb，et al. Optimum refractive index of poly-component particulate systems for measurement of particle size distribution by laser diffraction method analyzer［J］.Materials Chemistry and Physics，2009（117）：18-22.

［7］ Yuan Y Y，Hong L，Shuai Y，et al.Inverse problem for aerosol particle size distribution using SPSO associated with multi-lognormal distribution model［J］. Atmospheric Environment，2011，45（28）：4892-4897.

［8］ Fu Y，Zuo H F，Liu P P，et al.Gas path electrostatic sensor monitoring and comparison experiment on turbojet engine［J］.Trans Nanjing U Aero Astro，2013，30（4）：361-365.

［9］ Sun X G，Tang H，Yan G B.Study of inversion and classification of particle size distribution under dependent model algorithm［J］.Spectroscopy and Spectral Analysis，2008，28（5）：1111-1114.（in Chinese）［10］Albert R，Farrell P V.Droplet sizing using the shifrin inversion［J］.Journal of Fluids Engineering，1994，116：357-362.

［11］Zhou W，Cao W X，Sun Z H.Theoretical analysis on measuring particle-size distribution by Shifrin transform［J］.The Journal of Light Scattering，2007，19（3）：236-241.

［12］Dai B，Yuan Y N，Bao Z H，et al.An improved method for inversion of particle size distribution from scattering spectrum［J］.Spectroscopy and Spectral Analysis，2011，31（2）：539-542.（in Chinese）

［13］Han Y，Yang Z L，Yuan Y N，et al.A noise removal method in measurement of particle size distribution by the Shifrin transform［J］.Advanced Materials Research，2014，1058：93-96.（in Chinese）

［14］Dai B，Luo X D.Multiple light scattering of nonspherical particles with elliptical cross section［J］. Acta Physica Sinica，2009，58（6）：3864-3868.

［15］Ghatak A K，Thyagarajan K.Contemporary optics［M］.New York，USA Plenum Press，1978.

［16］Cheng Shouzhu，Jiang Zhiyong.Physics［M］.Bei jing：Higher Education Press，1998.（in Chinese）

（Executive editor：Zhang Tong）

O324 Document code：A Article ID：1005-1120（2015）04-0446-06

*Corresponding author：Dai Bing，Professor，E-mail：d.bing@ntu.edu.cn.

How to cite this article：Han Yue，Yang Zongling，Qiao Xing，et al.Resolution increase and noise removal in particle size distribution measurement with Shifrin transform［J］.Trans.Nanjing U.Aero.Astro.，2015，32（4）：446-451.

http：//dx.doi.org/10.16356/j.1005-1120.2015.04.446

（Received 4 September 2014；revised 1 March 2015；accepted 13 March 2015）