基于MATLAB的车辆转向传动机构设计*

石 坤，刘西侠，袁 磊

(装甲兵工程学院机械工程系，北京 100072)

0 引言

多轴车辆在转向时，存在低速转向半径过大和高速转向稳定性欠佳等问题。轮式车辆转向半径过大，使其在狭窄的道路中通过性降低，转向灵活性受到限制;且高速时车辆稳定性不好，易导致车辆部分轮胎侧滑严重［1］。因此，设计开发出新的转向系统来取代当前的双前桥转向系统，具有重要意义［1］。

全轮转向系统单轴方案如图1所示。系统工作时，比例阀接受由ECU控制单元发出的电信号指令，连续地控制比例阀输出的压力、流量等参数，驱动液压缸活塞杆运动来克服车轮转向所引起的转向阻力，使车轮转动由ECU控制器计算出的转角，实现全轮转向。为了使车轮能够转动预期转角，须对转向传动机构进行合理设计，使机构能够配合液压缸的运动，进而实现对车轮转角的控制。曲柄滑块式转向传动机构能够很好的跟液压转向装置配合，该机构性能较好，结构紧凑，且零部件相对较少，这使得该机构具有很强的实用性。

本文基于三轴车辆全轮转向系统方案，设计了相应的转向传动机构，并立了该机构的数学模型，并通过MATLAB软件进行设计计算。计算结果表明，由该机构所决定的转向曲线与理论阿克曼曲线能较好吻合。同时，该机构能够很好地与转向液压系统配合，进而实现对车轮转角的实时精确控制。

图1 全轮转向系统单轴示意图

1 转向传动机构运动分析

转向传动机构示意图如图2所示［2］。该曲柄滑块式转向传动机构具有结构简单、紧凑、转向灵活等特点，且转向半径小，符合全轮转向系统对转向传动机构的要求。设液压缸轴线到车轮轴线的安装距离为 e，梯形臂长(O1C、O2P)为 r，拉杆长(PQ、CD)为k，转向梯形底角为θ，左右车轮转向主销与梯形布置平面交点间的距离为m。当液压缸活塞杆向右移动时，外侧出轮转角为α，内侧车轮转角为β，设液压缸活塞位移为y。

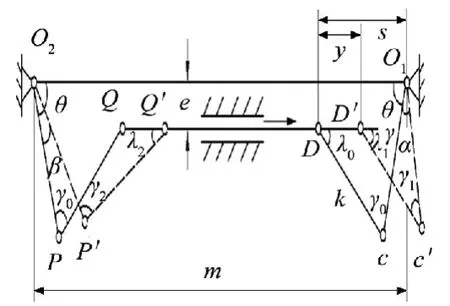
图2 转向传动机构示意图

当车轮转向时，以向左转向为例，此时右侧车轮为外转向轮。机构运动如图2所示，假设液压缸位活塞杆移为y，方向向右，通过右侧拉杆推动右梯形臂转动了一个角度α。则可得出活塞杆的位移y与右转向轮转角α的关系为:

同理，活塞杆的位移y与左转向轮转角β的关系为:

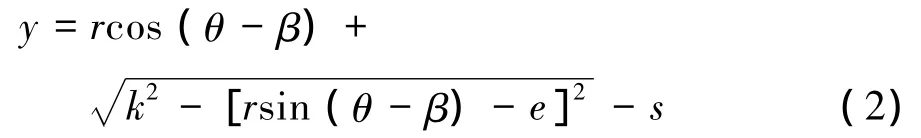
2 数学模型建立

2．1 目标函数

转向传动机构的设计目标是使由该机构运动所传递到车轮的转角尽可能地接近相对应的阿克曼理论转角。为了使车辆能够顺利转向，必须使转向中所有车轮的轴线都相交于一点，交点称为车辆的转向中心，以某型双前桥转向的车辆三维模型为例进行说明，如图3 所示［3］。

图3 车轮理论转角关系示意图

图中:αi为车辆i轴外侧车轮转向角;βi为车辆i轴内侧车轮转转角;m为轮胎两侧主销距离;Li为第i轴到车辆瞬时转向中心距离;O为轮式装甲车辆的瞬时转向中心。

车辆转向时，同一转向轴的理想内外轮转角满足如下关系:

设外侧转角αi为自变量，则由式(3)、(4)可将内侧转角βi表示为αi的函数，即:

由(1)、(2)两式整理可得内侧车轮实际转角为:

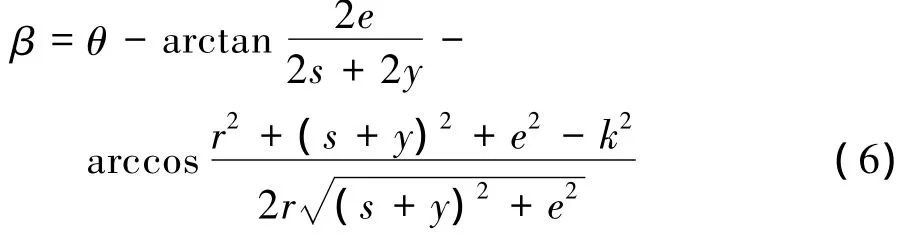
一般要求在整个转向过程中，内侧实际转角β与理论转角βi偏差的最大值应达到最小。则目标函数可表达为:

2．2 设计变量

针对某型三轴车辆进行分析讨论，其轴距L、左右车轮转向主销与梯形布置平面交点间的距离m均为给定值。拉杆的长度可根据公式计算得出:

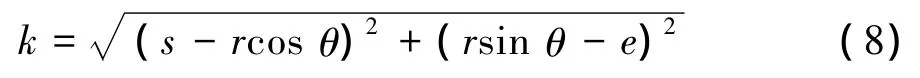
因此需要设计的参数为:梯形底角θ、梯形臂长r、安装距离e，以及拉杆始端D至主销与梯形布置平面交点O1在转向梯形平面的投影距离s。

2．3 约束条件

(1)最小传动角 在运动时，须考虑转向梯形机构传动角(梯形臂与拉杆所夹锐角)的变化。根据机械原理知，一般要求传动角γmin≥35°。由图2得最小传动角的表达式为:

式(9)中:

(2)安装距离e取值范围为［4］:

(3)梯形底角的取值范围为:

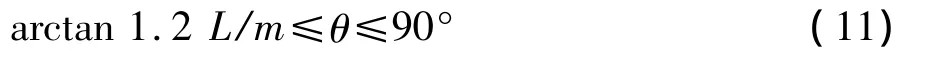
(4)梯形臂的取值范围为:

(5)保证液压缸结构具有实用的可能性，应满足:

(6)投影距离s的取值范围为:

2．4 数学模型

将以上目标函数和约束条件进行整理，即得到一个具有4个变量、10个约束函数的非线性优化模型。

目标函数:

H=min f(x)=min{max|βi－β|}

约束条件:

g1(x)=35°－γmin≤0

g2(x)=r－(s－r cos θ)sin 10°－e＜0

g3(x)=e－r sin(θ－βmax)－(s－r cos θ)sin 10°≤0

g4(x)=arctan 1．2L/m－θ≤0

g5(x)= θ－90°≤0

g6(x)=0．11 m－r≤0 g7(x)=r－0．22 m≤0

g8(x)=2 s+4 ymax－0．8 m≤0 g9(x)=0．8 m－s≤0 g10(x)=s－1．4 m≤0

3 仿真计算

已知某型三轴车辆的轴距为L1=1 900 mm，L2=3 800 mm，轮距为 m=2 469 mm，最大外轮转角为30°，在MATLAB软件中采用非线性优化命令进行优化，计算结果为:

θ=90°，r=480 mm，e=230 mm，s=350 mm。

计算得出拉杆长度为:

内转向轮实际转角与理论转角的偏差为:

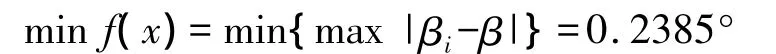
得到的仿真曲线如图4所示。

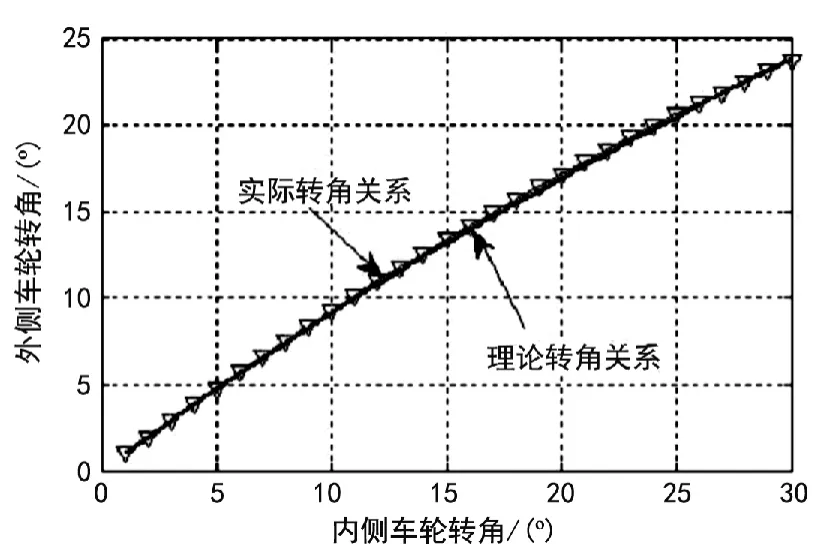
图4 车轮理论与实际转角关系曲线

由图4可看出，在外侧车轮的转角范围内，由转向梯形决定的实际转向曲线与理论阿克曼转向曲线总体吻合较好，这说明数学模型具有可行性。从计算结果和图5得出，内侧车轮实际与理论转角最大误差仅为0．2385°，有足够的精度。

图5 内侧车轮理论与实际转角偏差图

4 结论

(1)基于一种曲柄滑块式转向传动机构进行理论分析，并利用MATLAB进行设计计算，确定目标函数、设计变量和约束条件，对该机构进行优化设计。结果表明，由该机构所决定的转向曲线与理论阿克曼曲线基本一致，验证了所建立的数学模型的可靠性。

(2)该机构简单紧凑，转向灵敏，能够很好地与转向液压系统配合，能实现对车轮转角的实时精确控制。且车轮理论与实际转角误差较小，有较高精度。

［1］ 洪升耀，徐国英，刘西侠，等．三轴车辆全轮转向系统设计及转向性能分析［J］．机械研究与应用，2013(3):20－22．

［2］ 农 琪，谢业东．基于MATLAB的叉车曲柄滑块式转向机构的优化设计［J］．制造业自动化，2010(12):33－35．

［3］ 洪升耀．多轴轮式装甲车辆全轮转向动力学研究［D］．北京:装甲兵工程学院，2013．

［4］ 周祥基．汽车转向传动机构的类型分析与优化设计［D］．南京:东南大学，2005．

［5］ 袁 磊，刘西侠，金 毅．一种具有不同转向模式的多轴转向车辆设计［J］．机械设计与制造，2012(10):33－35．

［6］ 喻 凡，林 逸．汽车动力学［M］．北京:机械工业出版社，2008．

［7］ 余志生．汽车理论［M］．北京:机械工业出版社，1990．

［8］ 王树风，李华师．三轴车辆全轮转向最优控制［J］．汽车工程，2013，35(8):667－672．