模糊神经网络在驼峰机车推峰速度控制中的应用*

何 霄

(中铁二院西北勘察设计有限责任公司站后综合处，甘肃兰州 730000)

0 引言

当前，自动化驼峰已经形成了推峰机车无线遥控、车组溜放速度自动控制的自动化控制能力，可以传递和共享信息的CIPS系统，极大提高了编组站的解体编组效率。虽然对推峰机车的控制已经达到不用司机在驾驶室操作的水平，但该控制方式下，机车推峰速度的大小仍然凭人的经验判断，无法保证当前推峰速度即为最优速度，而且推峰过程中包含多个复杂的变量，对速度的计算容易受到钩车长度、重量，峰顶与驼峰尾部距离及与前行钩车的距离等因素的影响。论文在考虑到诸多因素后，提出用模糊神经网络的智能算法［1－2］，通过建立合理的网络模型来实现推峰机车速度的精确控制，利用模糊控制理论鲁棒性和容错能力强的特点及神经网络自学习和训练的能力，得到最优的速度控制模型。

1 影响机车推峰速度的因素

1．1 前后两钩车摘钩点的距离差值

即前行钩车完成摘钩作业的地点与当前钩车摘钩地点在距离上的差值。在车组溜放过程中，相邻钩车之间须保持一定距离的安全间隔，以免溜放车组因分路道岔转换不及时而造成车辆掉道或挤坏道岔的现象。根据运动物体速度与距离的关系，若正在溜放的钩车与峰顶即将提钩的构成间距越大，则应适当加快机车推峰速度，有利于提高作业效率;反之则减小推峰速度，避免速度过快导致溜放途中两钩车碰撞［3］。对于相同作业计划，其车组数量和长度是固定不变的，所以决定相邻溜放车组间距的因素为不同的摘钩地点的选取。

1．2 溜放车组走行性能引起的时间差异

进行溜放作业的钩车可根据走行性能的不同分为难行车(一般为轻车或空车，产生的重力加速度较小)和易行车(一般为重车，产生的重力加速度较大)，确定机车推峰速度时，相邻钩车走行性能的大小决定机车推峰速度的变化。若前车是难行车，后车是易行车，则推峰速度就应适当减小;若前车易行后车难行，要适当提高推峰速度。假设给机车恒定的推峰速度V，则相邻钩车通过峰顶的时间差t应满足:

式中:l为车组长度。

1．3 前行钩车的速度

如果相邻两车组溜放过程的时间差最短，则此时机车达到最优推峰速度。如果前行车组速度越大，则推峰速度应适度增大，保证当前车组以合理的速度进入溜放坡，提高解体作业效率。

1．4 前行车组所经过的分路道岔位置到峰顶的距离

如果该距离较大，相邻车组共同走行的距离将随之增大，应该及时降低推峰速度，使当前车组与前行车组保持安全间隔距离，确保当前车组在分路道岔转到位之前到达相应道岔。

2 基于模糊神经网络的推峰速度控制模型

2．1 对所输入变量模糊化处理

(1)前后两钩车摘钩点的距离差值模糊化处理。如果前行钩车中车辆数较多(有可能整车溜放)，当前钩车的车辆数最少为1，则摘钩点距离的差值论域可定为［0，100］，同时赋予5个语言变量值很小(VS)、小(S)、中(M)、大(B)，很大(VB)，可得到各语言的隶属函数如式(2)所示:

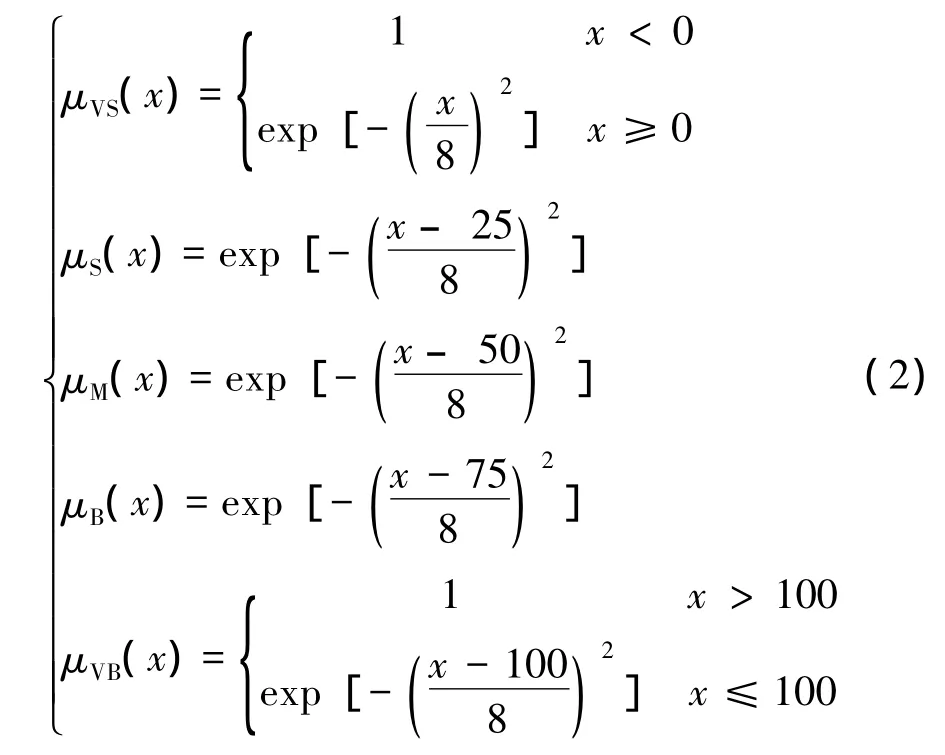
(2)溜放车组走行性能引起的时间差异的模糊化处理。考虑到溜放过程的特殊情况，可能存在相邻钩车的车辆数相差很多的现象，时间差=L(几乎等于带解车组长度)/V(平均速度)，应该相差30 s，所以取论域为［－15，15］，赋予 3个语言变量小(S)、中(M)、大(B)，隶属函数如式(3)所示:

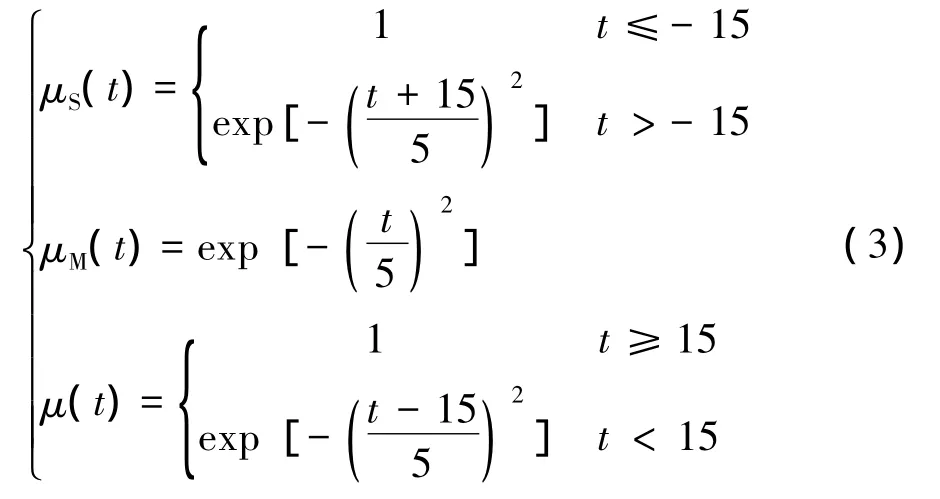
(3)前行钩车速度的模糊化处理。调机推峰速度按规定不能超过15 km/h，正常情况下最低为3 km/h，论域为［3，15］，赋予5 个语言变量值VS、S、M、B，VB，隶属函数如式(4)所示:

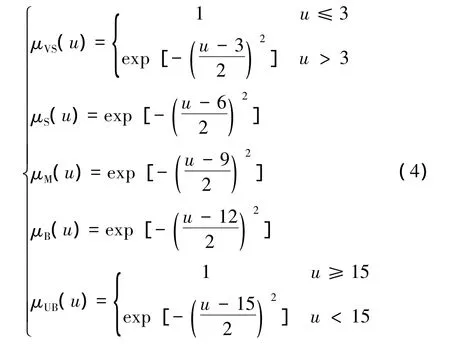
(4)前行车组所经过的分路道岔位置到峰顶的距离的模糊化处理。编组站溜放坡的第一分路道岔距峰顶的距离不少于30 m，最后一个分路道岔距峰顶一般不超过150 m，所以距离的论域为［30，150］，赋予3个语言变量S、M、B，隶属函数如式(5)所示:

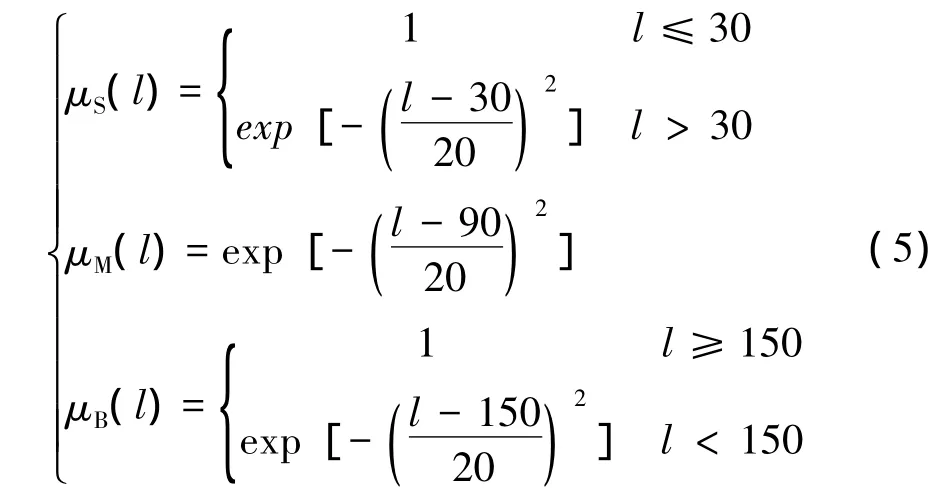
2．2 建立模型

根据模糊系统的标准模型，设计了控制驼峰推峰速度的模糊神经网络模型。此模糊神经网络控制器为四输入单输出系统，输入为影响机车推峰速度的因素，X表示前后两钩车摘钩地点的距离差值、U表示前行车组推峰速度、T表示溜放车组走行性能差异、L表示前行车组所经过的分路道岔位置到峰顶的距离。如图1所示。

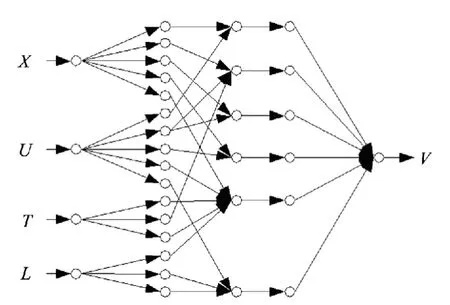
图1 推峰速度模型

3 基于模糊神经网络的学习算法

采用误差反向传播的迭代算法［4］。为此对每个神经元的输入输出关系加以形式化描述。推峰速度的误差函数定义为:

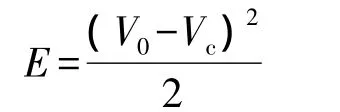
式中:Vc是实际计算输出，V0是样本。

学习目标就是使E小于预定义的误差。设取误差代价函数为:

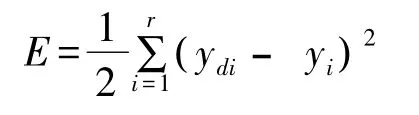
可以得出参数调整的学习算法为:

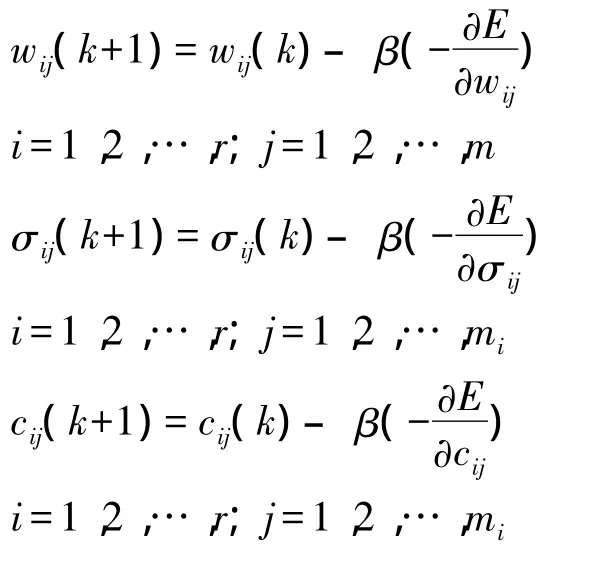
4 仿真过程

从编组站CIPS系统中得到原始数据组，这里只需要实际股道、实际辆数、实际重量、给定推峰速度、实际推峰速度五类数据，从中取490组数据作为学习样本训练，10组作为测试样本与仿真结果对比，用对比结果说明仿真的准确性［5］。取0．001为误差平方和，经过485次训练之后达到要求。如图2为训练过程图，表1为训练后部分参数表:

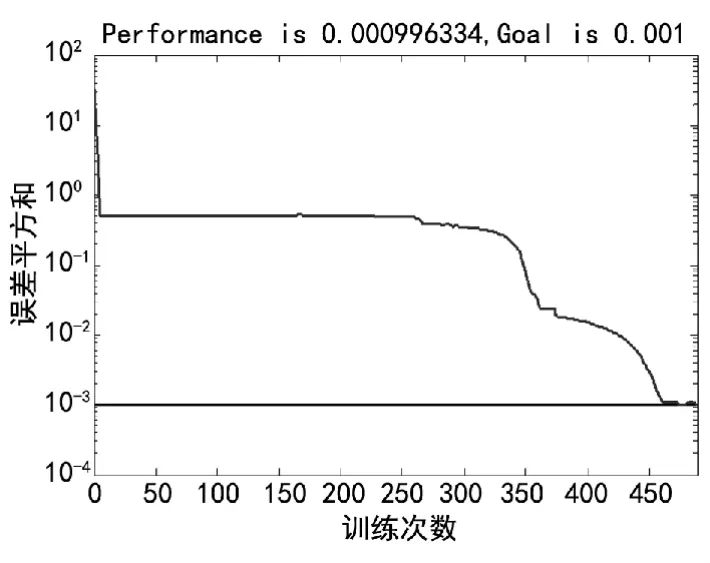
图2 训练过程图

表1 训练后部分参数表

将10组测试数据作为输入信息，经仿真后的输出结果与测试样本结果相比较，得到图3的结果。*表示模拟速度，曲线为样本速度，从图中可以看出，利用模糊神经网络建立的机车推峰速度模型与机车实际推峰速度基本相似，因此证明论文利用模糊神经网络控制机车推峰速度是可行的。

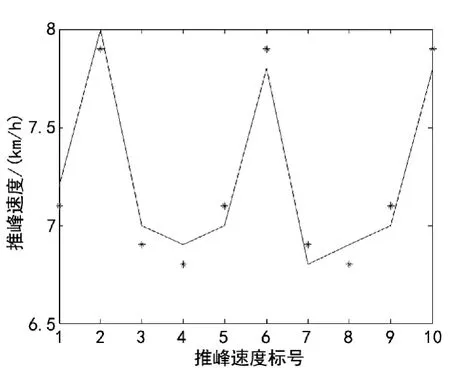
图3 测试图

在验证了用模糊神经网络控制机车推峰速度的可行性后，选取某一段时间机车运行速度曲线作为参照，与模糊神经网络计算的速度进行对比，进一步验证模糊神经网络控制推峰速度的可靠性。在编组站作业计划中任选两钩计划，第一钩车从峰顶到驼峰尾部运行时间为3～25 s，另一个钩车的运行时间为25～43 s，模型的时间周期设定为2 s，通过神经网络模型计算机车运行速度。如图4为模拟速度与实际运行速度的对比

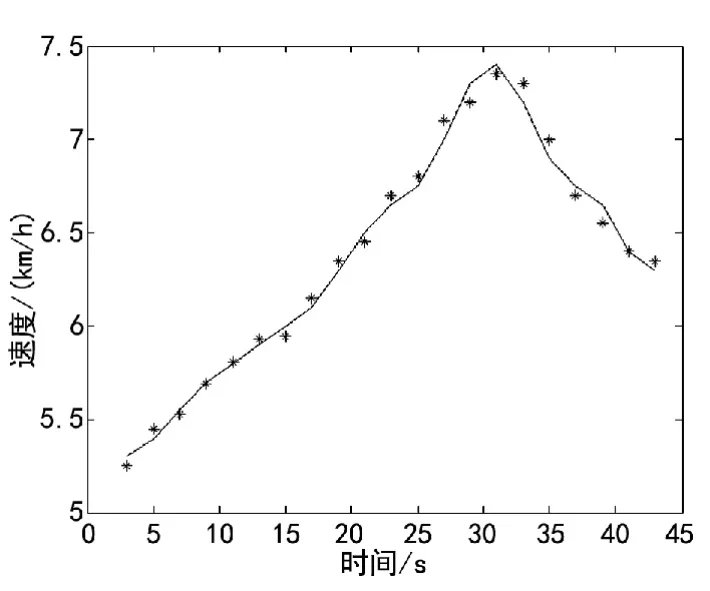
图4 模拟速度与实际速度对比

图4 中连续的曲线为机车实际运行速度，*表示用模糊神经网络计算出的模拟速度。从图中可以看出，模拟速度与实际运行速度相差甚小。另外，人工控制机车速度的过程完全凭个人经验，会出现在某一动及旋转的载荷下加工的。可以借助于软件对其加工过程中的振动情况进行仿真和分析，从而可以对振动幅度进行有效地减小。另外，中心孔是定位、校验轴类零件的基准，无论是中心孔的深度，还是其锥度的大小、两端之间的同轴度都对加工轴类零件有着很大的影响，这也是今后在对细长轴加工精度提高时所需要考虑和解决的重要问题之一。

［1］ 宋颖杰，徐 琳．浅谈中心轴与孔类加工［J］．应用技术，2013(9):72-73．

［2］ 郭建亮，崔伯第．基于切削力测量的细长轴加工误差在线补偿［J］．机床与液压，2005(5):86-89．

［3］ 武文革，庞思勤．可逆向车削细长轴加工误差分析［J］．北京理工大学学报，2004，2(2):86-89．

［4］ 王小翠，李 蔚．细长轴车削用量优化与加工变形误差补偿技术的研究［J］．工艺与检测，2007(7):85-88．

［5］ 戴海港．轴类零件弯曲变形在线检测研究［D］．成都:西华大学机械学院，2011．

［6］ 谢新伟，赵千红，徐国荣，等．减缓车削加工时细长轴震动的方法［J］．应用能源技术，2007(9):9-10．

［7］ 张新运，王小翠，李 蔚．车削加工误差补偿技术的研究［J］．西安工程大学学报，2009，8(2):56-58．

［8］ 王小翠，李 蔚．细长轴车削用量优化与加工变形误差补偿技术的研究［J］．工艺与检测，2007(7):85-88．

［9］ 江 平．细长轴车削加工过程的有限元仿真分析［D］．成都:西华大学机械学院，2012．

［10］ 武文革，庞思勤．可逆向车削细长轴加工误差分析［J］．北京理工大学学报，2004，2(2):86-89．

［11］ 叶又东．数控铣削加工中的工艺分析及处理［J］．机械，2004(10):40-42．