基于有限元方法的齿轮箱动态响应分析*

荆焕亮，吴鹏翔，王洪福，段海华，岳晓露

(河南神州重型封头有限公司，河南新乡 453731)

0 引言

齿轮箱是各种机械设备中应用最广泛的动力和运动传递装置，具有功率恒定、传动效率高等特点，已成为现代化工业中最重要的零部件之一。随着齿轮箱朝着大型化、高速化、轻量化、高精度方向发展，对振动及噪声要求也越来越高［1－2］。

传统齿轮箱设计主要停留在静态设计阶段，对动态特性考虑较少，而在齿轮箱运转过程中，由于齿轮啮合对数的变化、齿轮的受载变形、齿轮误差等原因，导致啮合过程中轮齿动态啮合力的产生，齿轮副受到这种内部激励引起齿轮振动，齿轮振动再经轴传递到轴承座，再有轴承座传到箱体，激起箱体振动［3］。笔者将用有限元法对齿轮箱进行动态特性计算分析，在齿轮箱设计前期就可对其性能进行评估，并为动态优化提供理论指导，缩短开发产品周期。

1 有限元模型建立

该齿轮箱采用Proe/E进行几何模型的建立，然后利用有限元软件Virtual．Lab进行有限元模型建模。在进行有限元模型建立时，要全面准确的反应模型，也要考虑有限元软件计算效率，需要对齿轮箱简化建模，去除齿轮箱一些螺栓、较小倒角和圆角。划分完成后的齿轮箱有限元模型如图1所示。

结合该齿轮箱安置工况，定义边界条件如图2所示，齿轮箱通过箱体上螺栓连接固定在基座上，有限元模型中，通过耦合单元把节点和螺纹孔处节点耦合在一起，并完全约束节点处六个自由度。齿轮箱工作过程中，啮合力通过齿轮传递给轴，轴在传递到轴承，最后通过轴承将力最终传递到齿轮箱上，通过RBE3单元耦合轴承周边单元节点，然后将作用力施加到耦合单元节点处。

图1 齿轮箱三维模型有限元图

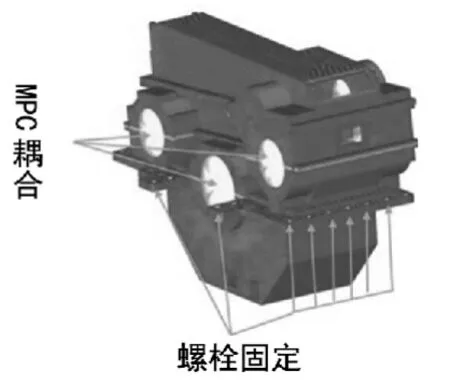
图2 边界条件示意图

2 齿轮箱动力学分析

2．1 齿轮箱模态分析

模态分析是结构动力学分析的基础，其主要目的是得到结构的一些固有特性，比如模态频率、模态振型、模态阻尼等。笔者选用Block Lanczos法进行求解，该求解采用稀疏矩阵进行求解，适用于齿轮箱这类大型对称结构的有限元模型，可以求得子空间法求解任何结构，且收敛速度更快［4］。

根据振动理论，结构的低阶模态对振动响应的影响较大，高阶模态可以忽略不计，得到模型模态频率如表1所列(只列出前20阶模态频率)，图3为前10阶齿轮箱模态振型图。

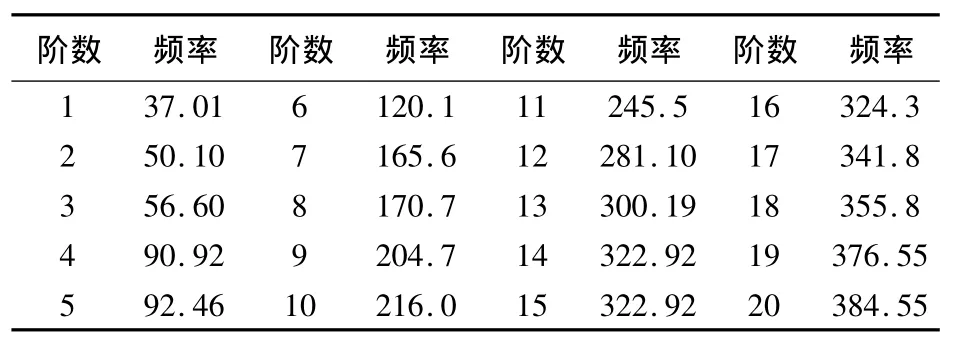
表1 齿轮箱模态频率 /Hz

图3 模态振型图

计算结果表明，齿轮箱最低固有频率为37 Hz，当齿轮箱输入转速为850 r/min，1 000 r/min时，输入轴的转频分别为14．17 Hz和16．67 Hz，可见齿轮箱最低固有频率远大于输入轴的转频，此转速下齿轮啮合频率为368 Hz和433．07 Hz。

2．2 基于模态频率响应分析

谐响应分析是用于确定线性结构在承受一个或多个随时间按正弦(简谐)规律变化的载荷时稳态响应的一种技术。该分析的目的是计算出结构在几种频率下的响应并得到一些响应值(通常是位移)对频率的曲线。

对于谐响应分析，其控制方程为［5］:

式中:K为刚度矩阵;M为质量矩阵;材料是线弹性的、使用小位移理论(不包括非线性);C为阻尼;F1、F2为激振力。

谐响应的求解方法有完全法，缩减法和模态叠加法3种。其中，完全法是一种最简单的方法，使用完全结构矩阵，允许非对称矩阵的计算，但是不能进行预应力的计算;而缩减法需要选择主自由度，根据主自由度得到结构近似的质量矩阵和阻尼矩阵;模态叠加法是基于模态分析的方法，是3种方法中计算最快的一种方法。采用模态叠加法的频率响应分析。

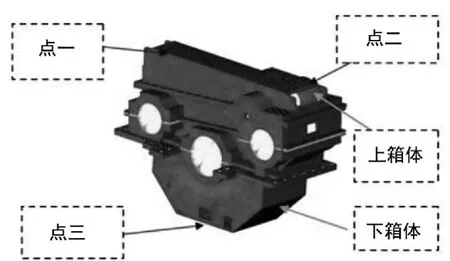
图4 振动节点位置示意图

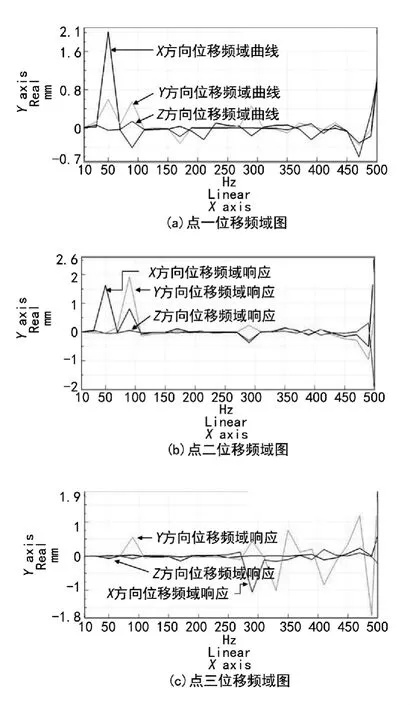
图5 频域振动位移图

对图4给出所选取齿轮箱三节点位置，对齿轮箱进行频率响应分析，得所标注节点振动位移频域图如图5所示。

由图5知，上箱体在第二阶固有频率为50 Hz，第四阶固有频率为90 Hz附近时振动位移较大，即转速115 r/min，207 r/min时激励振幅最大，此时齿轮箱发生共振现象，高阶频率更容易激励下箱体振动，共振频率为 289 Hz，355 Hz，455 Hz附近，即转速 667 r/min，819 r/min，1 050 r/min容易激励下箱体振动。因此，齿轮箱输入转速时尽量避免115 r/min，207 r/min，667 r/min，819 r/min，1 050 r/min 的转速，以避免齿轮箱发生共振现象。

3 结论

采用结构有限元法完成了齿轮箱动态响应分析，该方帮助工程师预测齿轮箱性能，缩短了设计周期，节省设计成本。本文通过齿轮箱模态分析，得到齿轮箱模态频率和模态振型，通过频率响应分析可知，齿轮箱输入转速时尽量避免115 r/min，207 r/min，667 r/min，819 r/min，1 050 r/min 的转速，以避免齿轮箱发生共振现象。

［1］ 唐定国，陈立民．齿轮传动技术的现状和展望［J］．机械工程学报，1993，20(3):35－41．

［2］ 王 建，罗善明，陈立锋，等．余弦齿轮轮齿刚度的有限元分析［J］．机床与液压，2008，36(5):236－238．

［3］ 童双双．齿轮箱动态响应分析与噪声预测［D］．大连:大连理工大学，2008．

［4］ 李有堂，机械振动与理论［M］．北京:科学出版社，2012．

［5］ 陈道礼，饶 刚，魏国前．结构分析有限元法的基本原理及工程应用［M］．北京:冶金工业出版社，2012．